abc367d题&信友队普及组比赛总结

先说abc367d

这一道题和这一道k倍区间有着异曲同工之妙，但是这道代替究竟难在哪里呢？？？

难在

环形

如何解决？

要用到这道题的解决方法。

翻倍

所以这道题可以说是这两道题的结合体。

赛时思路也想对了，那为何没有做出来？

对于一个位置如果是≥n的，那么需要消除掉i−n的影响，这样才能维护所选择区间长为 N的性质

赛时就是卡在对于这个点上才没有做出来。

来看一下AC代码

$AC$ $Code$

#include <bits/stdc++.h>

#define int long long

using namespace std;

int n;
int m;
int a[400010];
int cnt[1000010];
int sum[1000010];

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        a[i + n] = a[i];
    }
    for (int i = 1; i <= 2 * n; ++i)
    {
        sum[i] = sum[i - 1] + a[i];
    }
    cnt[0] = 1;
    int ans = 0;
    for (int i = 1; i <= n + n; ++i)
    {
        if (i >= n)
        {
            cnt[sum[i - n] % m]--;
        }
        if (i >= n + 1)
        {
            ans += cnt[sum[i] % m];
        }
        cnt[sum[i] % m]++;
    }
    cout << ans << "\n";
    return 0;
}

信友队8月月赛

这场比赛最大的遗憾与坑点就在于没有考虑到数学 \(Mod\) 的性质

取模在数学中是这样的

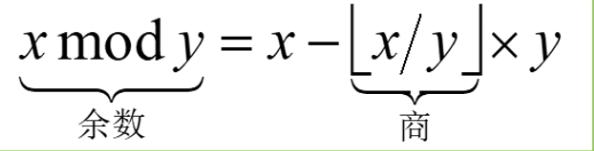
B题写的明明就是容斥原理的正解，但是有可能等于负数，所以需要进行先+p再%p的操作

白白丢掉 \(\color{Red}\texttt{20Pts}\)

A:

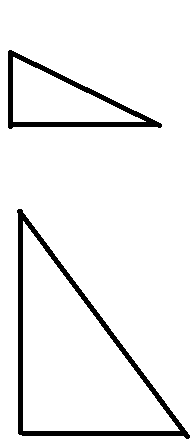
由上方的图片确定 \(a \lt c \leq \sqrt{a^2+b^2}\)

通过将每一个输入转化为区间，根据右端点排序得到答案。

B

写的就是正解，不说了。

C

这一题就是检查覆盖情况，具体见官方题解

D

比较奇特，先对于每个数进行异或，然后存放到map里面，每次查找就能得到结果了

$AC$ $Code$

#include <bits/stdc++.h>
using namespace std;

map<int,int> mp;
int n;
int k;

signed main()
{
    freopen("202408F.in", "r", stdin);
    freopen("202408F.out", "w", stdout);
    cin>>n>>k;
	basic_string<int> a(n+1,0);
    for(int i=1;i<=n;++i){
        cin>>a[i];
    }
    mp[0]=0;
    int s=0;
    int ans=0;
    for(int i=1;i<=n;++i){
        s=s^a[i];
        if(mp.find(s^k)!=mp.end()){
            ans=max(ans,i-mp[s^k]);
        }
        if(mp.find(s)==mp.end()){
            mp[s]=i;
        }
    }
    cout<<ans<<"\n";
}