2024.7.27清北学堂集训day5

2024.7.27清北学堂集训day5

就算你一道题不会，把你该拿的分拿到，不影响你拿高分 ——zhx真理

T1

这一道题号是很简单的，不一定算图论的部分，dfs判断一下图是否连通，因为如果不联通就没有最小生成树，最后排序输出前 \(n-1\) 条边的和

点击查看代码

#include <bits/stdc++.h>

#define int long long

using namespace std;

int n,m;
int u,v;
int d[450010];

struct edge {
	int to;
	int w;
};

vector<edge> e[100010];
bool vis[100010];

void dfs(int x) {
	for(auto y:e[x]) {
		if(!vis[y.to]) {
			vis[y.to]=1;
			dfs(y.to);
		}

	}
}

signed main() {
	cin>>n>>m;
	for(int i=1; i<=m; ++i) {
		cin>>u>>v>>d[i];
		e[u].push_back((edge) {
			v,d[i]
		});
		e[v].push_back((edge) {
			u,d[i]
		});
	}
	sort(d+1,d+m+1);
	vis[1]=1;
	dfs(1);
	//cout<<1<<"\n";
	for(int i=1; i<=n; ++i) {
		if(vis[i]==0) {
			cout<<-1<<"\n";
			return 0;
		}
	}
	int sum=0;
	for(int i=1; i<=n-1; ++i) {
		sum+=d[i];
	}
	cout<<sum<<"\n";
}

T2

这一个题首先想到的是60分的部分分，然后优化。
百分之百的做法是怎样的？因为我们求的是连通块个数，所以进行相邻的连边即可

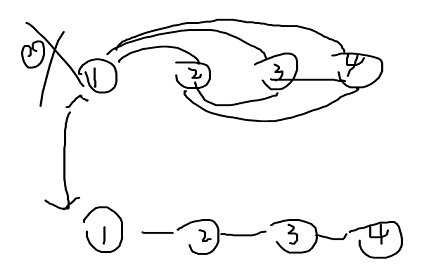
但是时间复杂度依然是 \(O(nm)\) 的，该怎么办？

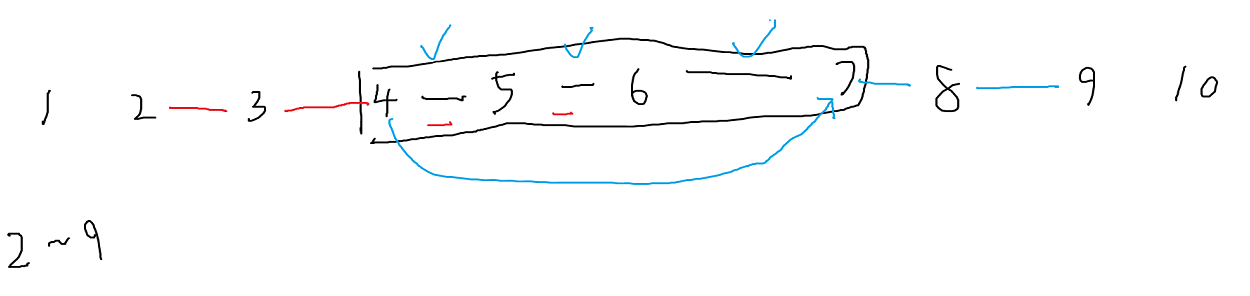
每次跳到根，每条边就只会被连接一次。

赛时加上了一个特判，成功从60pts------->0pts(。。

T3

很标准的图论题目，进行dijkstra/spfa,跑一遍最短路，记录 \(f_i,g_i\),代表走到i的方案数，走到i的最短路之和进行转移

注意，减法比取模快大概1000倍。注意加法时用，乘法有可能远远大于模数

进行最短路一定不要取模！！！一定！！！

为什么？因为如果一个边权为10000，模数100，边权就成为了0。。从最长路变成了最短路

点击查看代码

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<queue>
#include<algorithm>

using namespace std;

const int maxn=100010;
const int maxm=200010;
const int mo=1000000007;

#define inc(a,b) {a+=b;if (a>=mo) a-=mo;}

int n,m,en,dist[maxn],a[maxn],f[maxn],g[maxn];

bool inq[maxn];

queue<int> q;

struct edge {
	int e,d;
	edge *next;
}*v[maxn],ed[maxm];

void add_edge(int s,int e,int d) {
	en++;
	ed[en].next=v[s];
	v[s]=ed+en;
	v[s]->e=e;
	v[s]->d=d;
}

bool cmp(int a,int b) {
	return dist[a]<dist[b];
}

int main() {
	scanf("%d%d",&n,&m);
	for (int i=1; i<=m; i++) {
		int s,e,d;
		scanf("%d%d%d",&s,&e,&d);
		add_edge(s,e,d);
	}
	memset(dist,0x3f,sizeof(dist));
	dist[1]=0;
	q.push(1);
	inq[1]=true;
	while (q.size()) {
		int now=q.front();
		q.pop();
		inq[now]=false;
		for (edge *e=v[now]; e; e=e->next) {
			int newd=dist[now]+e->d;
			if (newd<dist[e->e]) {
				dist[e->e]=newd;
				if (!inq[e->e]) q.push(e->e),inq[e->e]=true;
			}
		}
	}
	for (int i=1; i<=n; i++)
		a[i]=i;
	sort(a+1,a+n+1,cmp);
	f[1]=1;
	g[1]=0;
	int ans1=0,ans2=0;
	for (int i=1; i<=n; i++) {
		int now=a[i];
		if (dist[now]==dist[0]) break;
		inc(ans1,dist[now]);
		inc(ans2,g[now]);
		for (edge *e=v[now]; e; e=e->next)
			if (dist[e->e]==dist[now]+e->d) {
				inc(f[e->e],f[now]);
				inc(g[e->e],f[now]);
				inc(g[e->e],g[now]);
			}
	}
	printf("%d %d\n",ans1,ans2);

	return 0;
}

T4

加上特殊性质，分数+20pts

+亿点点运气+20pts

+一点点实力+40pts(爆搜，考试必备)

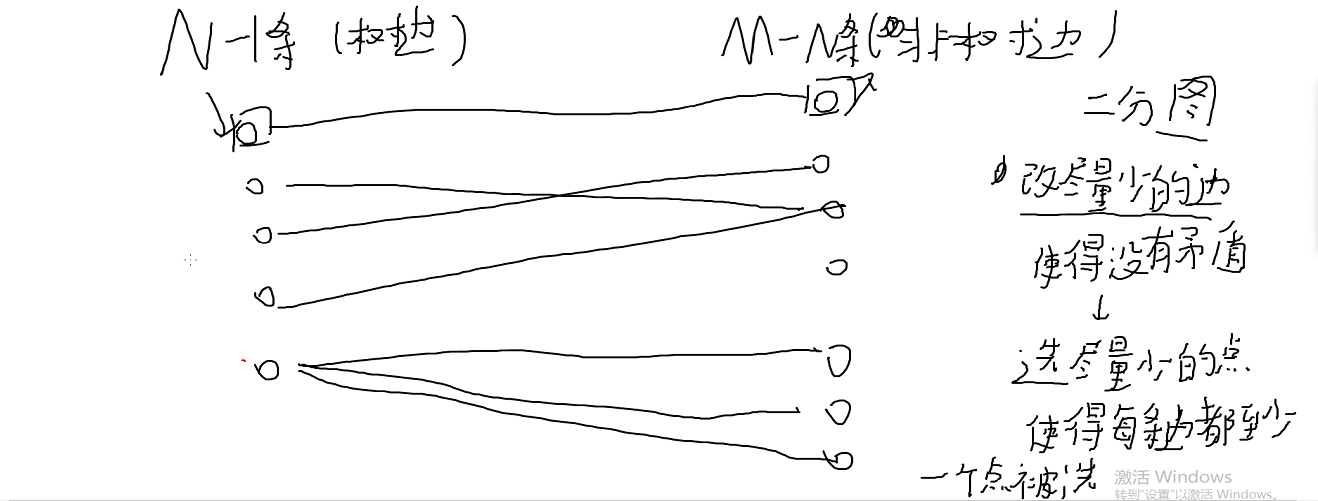
二分图匹配即可--------->匈牙利算法

---

匈牙利算法

就是为了解决上方二分图匹配的算法的

对于每一个左边的去匹配右边的

点击查看代码

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>

using namespace std;

const int maxn=110;
const int maxm=510;

int n,m,en,f[maxn],fd[maxn],fid[maxn],dep[maxn],result[maxm],match[maxn][maxm],use[maxm],s[maxm],e[maxm],d[maxm];

struct edge {
	int s,e,d,id;
	edge *next;
}*v[maxn],ed[maxn<<1];

void add_edge(int s,int e,int d,int id) {
	en++;
	ed[en].next=v[s];
	v[s]=ed+en;
	v[s]->e=e;
	v[s]->d=d;
	v[s]->id=id;
}

void dfs(int now,int fa) {
	dep[now] = dep[fa]+1;
	for (edge *e=v[now]; e; e=e->next)
		if (e->e != fa) {
			f[e->e] = now;
			fd[e->e] = e->d;
			fid[e->e] = e->id;
			dfs(e->e,now);
		}
}

bool dfs(int l) {
	for (int r=1; r<=m; r++)
		if (!use[r] && match[l][r]) {
			use[r]=true;
			if (!result[r] || dfs(result[r])) {
				result[r]=l;
				return true;
			}
		}
	return false;
}

int go(int p) {
	if (p==f[p]) return p;
	else return f[p]=go(f[p]);
}

int work(int r) {
	en=0;
	memset(v,0,sizeof(v));
	memset(f,0,sizeof(f));
	for (int i=1; i<=n; i++)
		f[i]=i;
	for (int i=1; i<=n; i++)
		if (r!=i) {
			if (go(s[i])==go(e[i])) return 0x3f3f3f3f;
			f[go(s[i])]=go(e[i]);
			add_edge(s[i],e[i],d[i],i);
			add_edge(e[i],s[i],d[i],i);
		}
	memset(dep,0,sizeof(dep));
	memset(fd,0,sizeof(fd));
	memset(match,0,sizeof(match));
	memset(f,0,sizeof(f));
	memset(result,0,sizeof(result));
	dfs(1,0);
	for (int i=n+1; i<=m; i++)
		if (i==r || i>n) {
			int p1=s[i];
			int p2=e[i];
			int d=::d[i];
			while (p1!=p2) {
				if (dep[p1]<dep[p2]) swap(p1,p2);
				if (d < fd[p1]) match[fid[p1]][i]=true;
				p1=f[p1];
			}
		}

	int ans=0;
	for (int i=1; i<=n; i++) {
		memset(use,false,sizeof(use));
		if (dfs(i)) ans++;
	}
	return ans;
}

int main() {
	scanf("%d%d",&n,&m);
	for (int i=1; i<=m; i++)
		scanf("%d%d%d",&s[i],&e[i],&d[i]);
	int ans=m+1;
	for (int i=1; i<=n; i++)
		ans=min(ans,work(i));
	printf("%d\n",ans);

	return 0;
}