CORIDIC算法学习记录
CORDIC算法叫坐标旋转数字计算法,由J.Volder在1959年提出,可以快速且简单的计算角度的数值。
问题
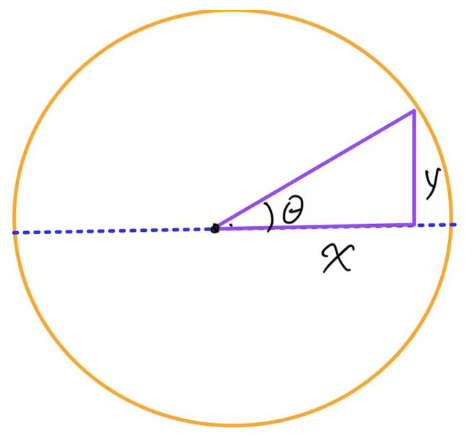
已知\(y,x\),如何快速计算角度\(\theta\)?
问题分析
许多人,直接求解\(\arctan(\frac{y}{x})\),但是反正切求解没有那么容易,如果要查表,由不得又要一堆操作下来,费事费力。虽然可以借助计算机求解,计算机只能加减乘除,计算反正切,需要级数展开,根据泰勒公式\(\arctan(x)=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\ldots\),可见包含了大量的乘法和除法,也不会快到哪里。
CORDIC算法原理
逼近方法及步骤
- 选择一系列标准角度,A=[45 26.5651 14.0362 7.12502 3.57633 1.78991 0.895174 0.447614 0.223811 0.111906 0.0559529 0.0279765 0.0139882 0.0069941]
- 将任何要计算的角度\(\theta\)与比较对象\(\beta\)比较,
- 第一次\(\theta\)与\(\beta\)取\(A_{(1)}=45^{\degree}\)比较,
- 若\(\theta>\beta=45^{\degree}\)时,增大\(\beta\),将\(\beta\)加上\(26.5651^{\degree}\)
- 再次比较\(\theta\)和\(\beta\)大小,当\(\theta > \beta\)就继续增加\(A\)的下一项,当\(\theta < \beta\)就继续减去\(A\)的下一项
- 直到\(\theta\)和\(\beta\)足够接近即可停止
例如:待测角度为\(53^{\degree}\),逼近过程用表格表示如下:
| 序号 | 初始值\(\beta\) | 比较结果 | 变化的值 | 符号 | 备注 |
|---|---|---|---|---|---|
| 1 | 45 | 1 | 26.5651 | + | |
| 2 | 71.5651 | 0 | 14.0362 | - | |
| 3 | 57.5289 | 0 | 7.12502 | - | |
| 4 | 50.4039 | 1 | 3.57633 | + | |
| 5 | 53.9802 | 0 | 1.78991 | - | |
| 6 | 52.1903 | 1 | 0.895174 | + | |
| 7 | 53.0855 | 0 | 0.447614 | - | |
| 8 | 52.611186 | 1 | 0.223811 | + | |
| 9 | 52.834997 | 1 | 0.111906 | + | |
| 10 | 52.946903 | 1 | 0.0559529 | + | |
| 11 | 53.0028559 | 0 | 0.0279765 | - | |
| 12 | 52.9748794 | 1 | 0.0139882 | + | |
| 13 | 52.9888676 | 1 | 0.0069941 | + |
最终为52.9958617,可以看到距离53已经很接近了,如果不够还可以继续。
可以看到,上边的比较过程,用眼观察并判断下一项的正负号比较容易,有人觉得直接比较大小,随着小数位数的增加,比较大小并不可靠。
> if(0.999999999999999999999999<1)
> a=10;
> end
以上代码中,我这里octave9.4中,小数点后16以前比较大小正确,超过就可能出错了,编程中小数比较大小不一定可靠。
逼近过程中的符号确定
- 将原角度对应的向量\((x,y)\)做相应角度的旋转,根据旋转后的纵坐标是否大于零,就知道下一次操作的正负号了
- 若旋转后的坐标\((x_1,y_1)\),根据欧拉公式\(x_1=x\cos\alpha-y\sin\alpha\),\(y_1=x\sin\alpha+y\cos\alpha\),其中\(\alpha\)为旋转的角度,方向与正负号有关
- 为了避免计算正余弦值,改造公式为:\(x_1=\cos\alpha(1-y\tan\alpha\),\(y_1=\cos\alpha(x\tan\alpha+y)\),我们只要能判断旋转后纵坐标\(y_1\)是否大于零,就能确定下次的旋转方向,无需计算\(\cos\alpha\),计算\(x\tan\alpha\)和\(y\tan\alpha\)
- 前面我们选择角度时取值的特征就是\(\tan(45^{\degree})=1\),依次为\(\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16}\ldots\),也就是说按照表里的角度值逼近时,无需计算正切值,每次都是前一个的\(\frac{1}{2}\)。是不是需要除法,计算机计算不需要,直接移位一次就能乘以或除以2了,是不是就很方便了。
根据角度计算正切值
- 对角度\(\theta\),则\(\tan\theta=\frac{\sin\theta}{\cos\theta}\),计算出\(\sin\theta,\cos\theta\);
- 由于\(\sin\theta=\frac{y}{r}\),\(\cos\theta=\frac{x}{r}\),单位圆内,知道\(x,y\)即可;
举个例子逼近\(\theta=50^{\degree}\)并求其正切值
使用的欧拉公式:
- 向量\((1,0)\)开始,向量的角度\(\alpha\)为\(0^{\degree}\)
- 小于目标,需要增大\(\alpha\),增大\(45^{\degree}\),$\begin{bmatrix}x_1\y_1\end{bmatrix}=\cos{(45^{\degree})}\begin{bmatrix}x-y\tan 45^{\degree}\x\tan 45{\degree}+y\end{bmatrix}=\cos45\begin{bmatrix}x_1{'}\y_1\end{bmatrix} \(,这里只需要移位和加减即可得到\)\begin{bmatrix}x_1{'}\y_1\end{bmatrix}$,前面的余弦值计算稍后处理
- 比较新的\(\alpha\),依旧小于目标,需要继续增加,虽然离目标只有\(5^{\degree}\),无法直接计算正切还有坐标,继续选择标准角度26.5651,经过旋转后,新坐标:$ \begin{bmatrix}x_1\y_1\end{bmatrix}=\cos{(45{\degree})}\cos{(26.5651)}\begin{bmatrix}x_1{'}-y_1\tan 26.5651{\degree}\x_1\tan 26.5651{\degree}+y_1\end{bmatrix}=\cos45{\degree}\cos{(26.5651)}\begin{bmatrix}x_2{'}\y_2\end{bmatrix} $此时的角度:\(71.5651\),
- 比较新的\(\alpha\),大于目标,需要减小,选择角度-14.0362,就这样一直进行下去,最终角度会越来越接近50度,例如经过8次旋转,角度为:\(45+26.5651-14.0362-7.12502-3.56733+1.78911+0.895174+0.447614=49.9601\),此时的误差已经很小了,如果不够继续即可;
- \(\begin{bmatrix}x_8\\ y_8 \end{bmatrix}=\cos(45)^{\degree}\cos(26.5651)^{\degree}\cos(-14.0362)^{\degree}\cos(-7.12502)^{\degree}\cos(-3.56733)^{\degree}\cos(1.78911)^{\degree}\cos(0.895174)^{\degree}\cos(0.447614)^{\degree}\begin{bmatrix}x_8^{'}\\ y_8^{'} \end{bmatrix}\)
而且以上连乘序列最终收敛到0.6072529,由于\(\cos\alpha=\frac{1}{\sqrt{1+(\tan\alpha)^2}}\),也就是说以上序列就成了$\prodn_{i=0}\frac{1}{\sqrt{1+{(2)}^2}} $
验证如下:
N=20;
A=zeros(1,N);
for i=0:1:N-1
A(i+1)=1./sqrt(1+2^(-2*i));
end
B=cumprod(A);
i=1:N;
%双y轴做图
yyaxis left
%scatter(i,A,'markeredgecolor',[0 .7 .8],'markerfacecolor',[0 .5 .6],'linewidth',2.5);
scatter(i,A,'markeredgecolor','r','markerfacecolor','g','linewidth',2.5);
xlim([-1 N+1]);
ylim([0.55 1.05]);
title('difference A and B');
xlabel('i');
ylabel('A changes')
yyaxis right
%scatter(i,B);
scatter(i,B,'markeredgecolor','b','markerfacecolor','r','linewidth',1.5);
ylim([0.55 1.05]);
ylabel('B,changes')
结果图就不放了,也就是说该多项式大概从第六项开始相乘时,就趋近与固定值0.6073了,以后无论怎么加项,角度在逼近,精度在提高,系统不再发生变化,随着N增加,A从第四项开始进入1%误差范围,从第七项开始,N每增加1,精度提高一个数量级,直到第27项开始matlab精度达到极值时,值为1.000000000000000不再变化。与A对应的B,从第4项开始进入到0.6系数中,从第7项开始进入0.6275开始进入精度稳定,直到第26项值为0.607252935008881,保持稳定不再变化。也就是说,才用CORDIC算法经过26次迭代,就可以实现几乎所有的精度要求。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号