视觉SLAM（四）相机模型 非线性优化

视觉SLAM（四）相机模型

1. 针孔相机模型与图像

小孔成像模型

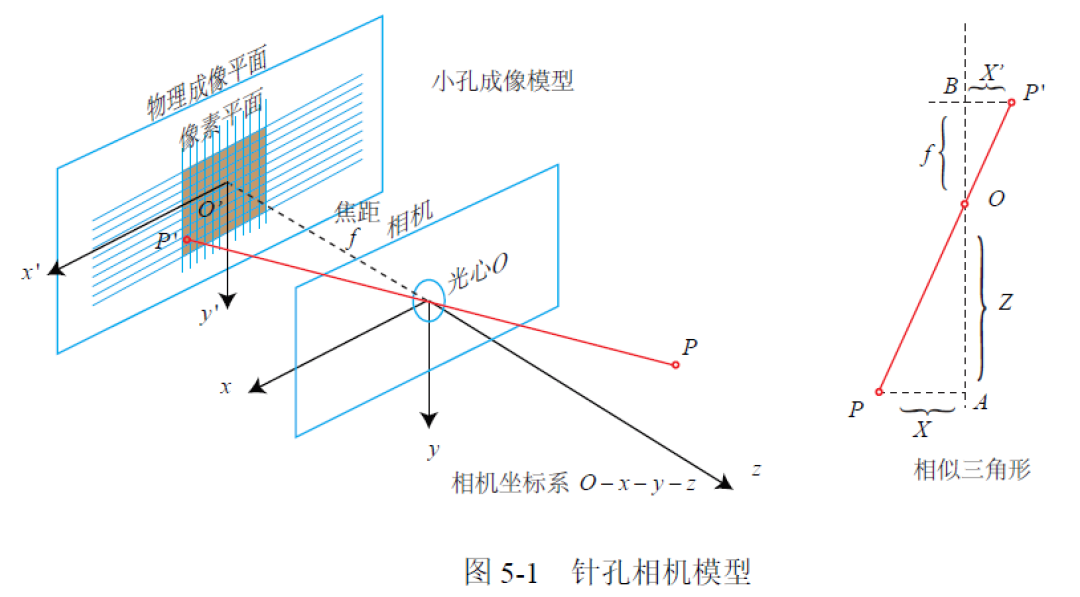
原始形式 \(\frac{Z}{f}=a\frac{X}{X'}=-\frac{Y}{Y'}\)
翻转倒前面 \(\frac{Z}{f}=\frac{X}{X'}=\frac{Y}{Y'}\)
整理得到：
\(X'=f\frac{X}{Z}\)
\(Y'=f\frac{Y}{Z}\)
成像平面到像素坐标

\[u=\alpha X'+c_x\\ v=\beta Y'+c_y \]

代入前边得到的式子可以得到

\[u=f_x\frac{X}{Z}+c_x\\ v=f_y\frac{Y}{Z}+c_y \]

通过上式就可以把空间点坐标投影到像素坐标系

矩阵形式：

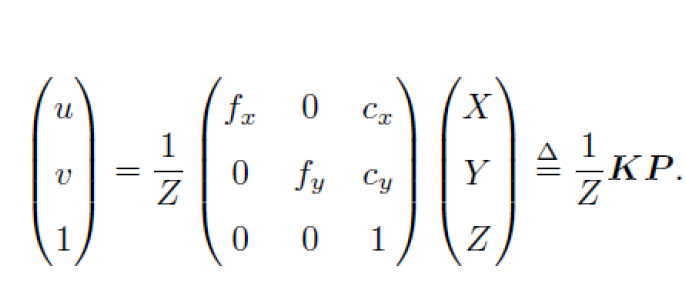
左侧是其次坐标 右侧是非齐次坐标 中间矩阵为内参数
内参通常在相机生产之后就已固定（内参矩阵可逆）

现实中，像素是方的，因此\(f_x \approx f_y\) 也是factor（f）

通过投影方程可以看出，同一直线上的投影点仍是同一个

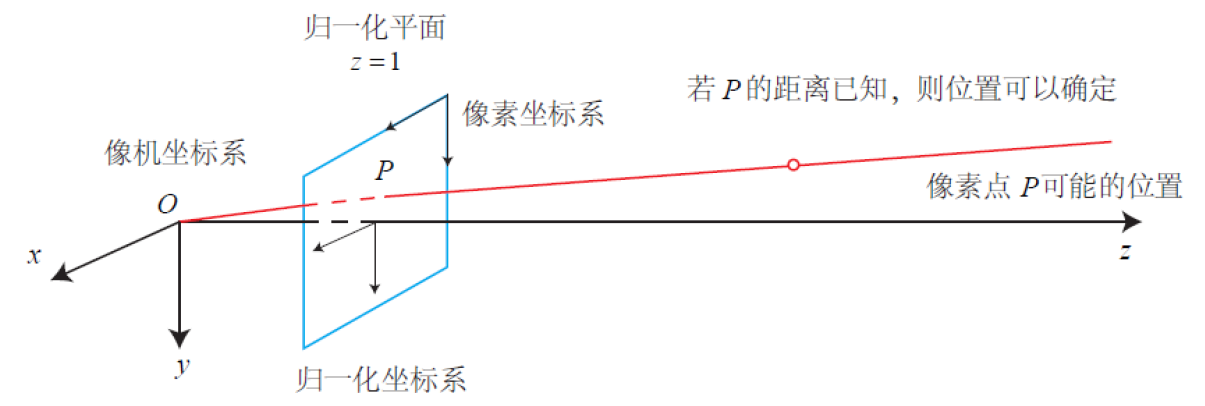
大部分都是在归一化平面上进行处理

除内参外，相机坐标系与世界坐标系还相差一个变换:

先把P 从世界坐标变到相机坐标系下.
• 这里 R, t 或 T 称为 外参(注：右侧式子隐含了一次非齐次到齐次的变换（见书）)
• 外参是 SLAM 估计的目标

投影顺序：世界-相机-归一化平面-像素

畸变

针孔前的镜头会引入畸变

例子

畸变类型

主要的畸变类型：径向畸变和切向畸变

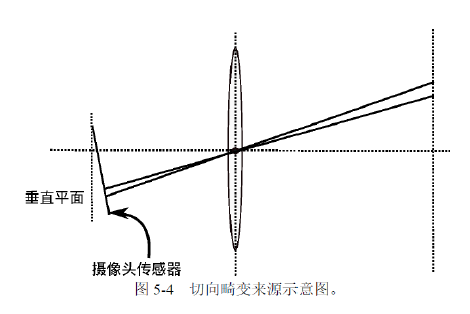
切向畸变来源

数学模型

畸变可以用归一化坐标的变换来描述

小结

1.首先，世界坐标系下有一个固定的点P，世界坐标为Pu
2.由于相机在运动，它的运动由R,t或变换矩阵T∈SE(3)描述。P的相机坐标为 \(\tilde{P}_c=RP_w+t. 3.这时的P仍有X,Y,Z三个量，把它们投影到归一化平面Z=1上，得到P的归化相机坐标：\)P_c=[X/Z,Y/Z,1]^T\(. 4.最后，P的归一化坐标经过内参后，对应到它的像素坐标：\)P_{un}=KP_c$

双目相机

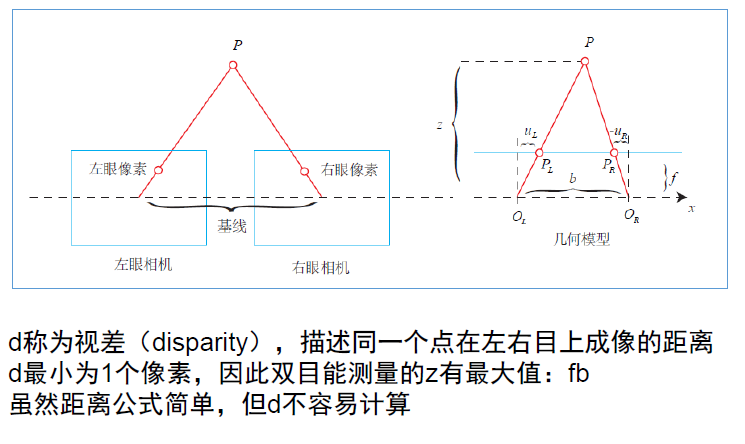
• 左右相机中心距离称为基线
• 左右像素的几何关系：

\[\frac{z-f}{z} = \frac{b-u_L+u_R}{b} \]

整理得

\[z=\frac{fd}{d},d=u_L-u_R \]

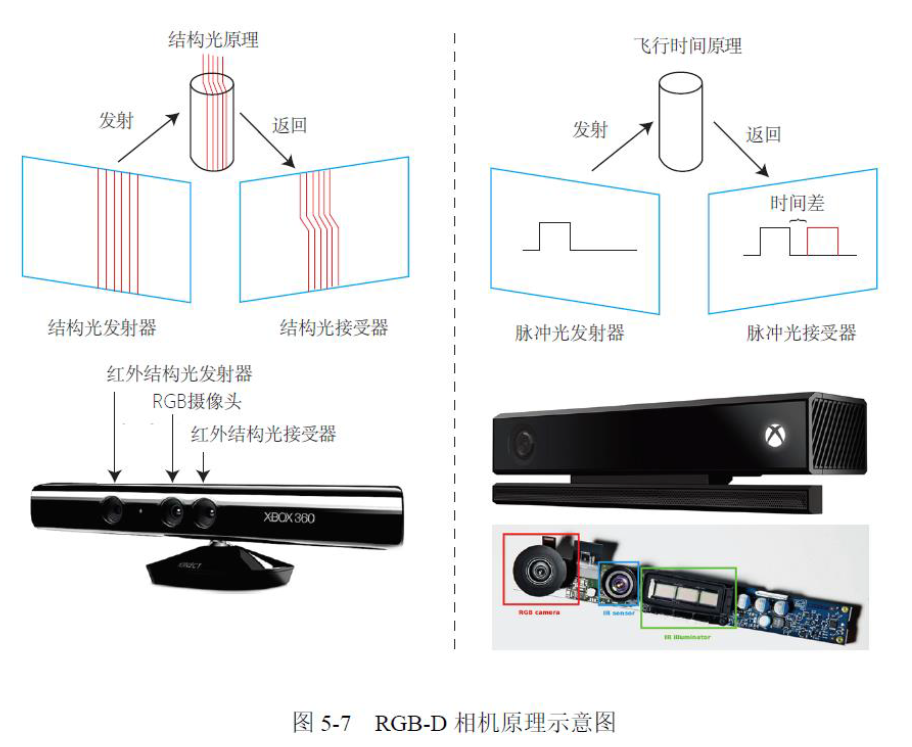
RGBD相机：物理手段测量深度

• ToF 或结构光两种主要原理
• 通常能得到与 RGB 图对应的深度图

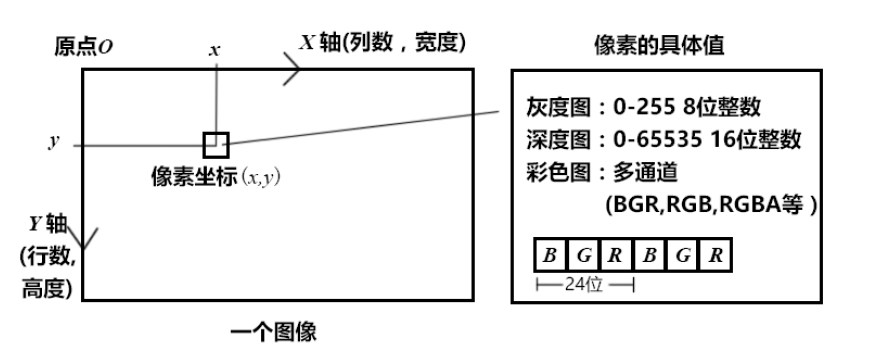
相机成像后，生成了图像
图像在计算机中以矩阵形式存储（二维数组）
需要对感光度量化成数值，例如0~255之间的整数（彩色图像还有通道）

2. 实践：OpenCV/RGBD图像拼接

3. 批量状态估计问题

观测模型

批量式（batch）

我们把状态最大似然估计变成了最小二乘问题

直观解释

• 由于噪声的存在，当我们把估计的轨迹与地图代入SLAM的运动、观测方程中时，它们并不会完美的成立。
• 此时就调整状态的估计，使得误差最小化
  该问题有何结构？
• 由许多个误差的平方和（或 Sigma范数和）组成。
• 虽然总体维度高，但每个项很简单，只关联2个变量。
• 如果用李代数表达位姿，那么是无约束优化问题如何求解？
  下面先来介绍通用的非线性最小二乘问题。

4. 非线性最小二乘法

迭代方式

1.给定某个初始值x0
2.对于第k次送代，寻找一个增量△k（问题：如何确定这个增量？），使得\(f{||(x_k+△x_k）||}^2\)达到极小值
3.若△:k足够小，则停止。
4.否则，令k+1=xk+△k，返回2

确定增量得方法（即梯度下降策略）：一阶得或二阶得

最速下降法和牛顿法虽然直观，但实用当中存在一些缺点

• 最速下降法会碰到 Zigzagl问题（过于贪婪）
• 牛顿法迭代次数少，但需要计算复杂的 Hessian矩阵
  能否回避 Hessian的计算？

1. Gauss-newton
2. Levenberg-marquadt

高斯牛顿法

G N 用 J 的表达式近似了 H

Levenberg-Marquadt方法

改进版的GN

1. 给定初始值xo，以及初始优化半径\(\mu\)。
2. 对于第ん次迭代，求解：\(\min_{\delta x_k}\frac{1}{2}||f(x_k)+J(x_k)\delta x_k||^2,st.||D\delta x_k||^2≤\mu\)
   这里\(\mu\)是信赖区域的半径，D将在后文说明。
   3.计算p.
3. 若\(\rho>\frac{3}{4}\) 则\(\mu=2\mu\)
4. 若\(\rho<\frac{1}{4}\),则\(\mu=0.5\mu\)
5. 如果p大于某國值，认为近似可行。令\(x_{k+1}=x_k+\delta x_k\).
6. 判断算法是否收敛。如不收敛则返回2,否则结束。
   
   LM相比于GN，能够保证増量方程的正定性
   即，认为近似只在一定范围内成立，如果近似不好则缩小范围从増量方程上来看，可以看成一阶和二阶的混合参数λ控制着两边的权重

小结

非线性优化是个很大的主题，研究者们为之奋斗多年
主要方法：最速下降、牛顿、G-N、L-M、 Dogleg等
与线性规划不同，非线性需要针对具体问题具体分析问题非凸时，对初值敏感，会陷入局部最优目前没有非凸问题的通用最优值的寻找办法问题凸时，二阶方法通常一两步就能收敛

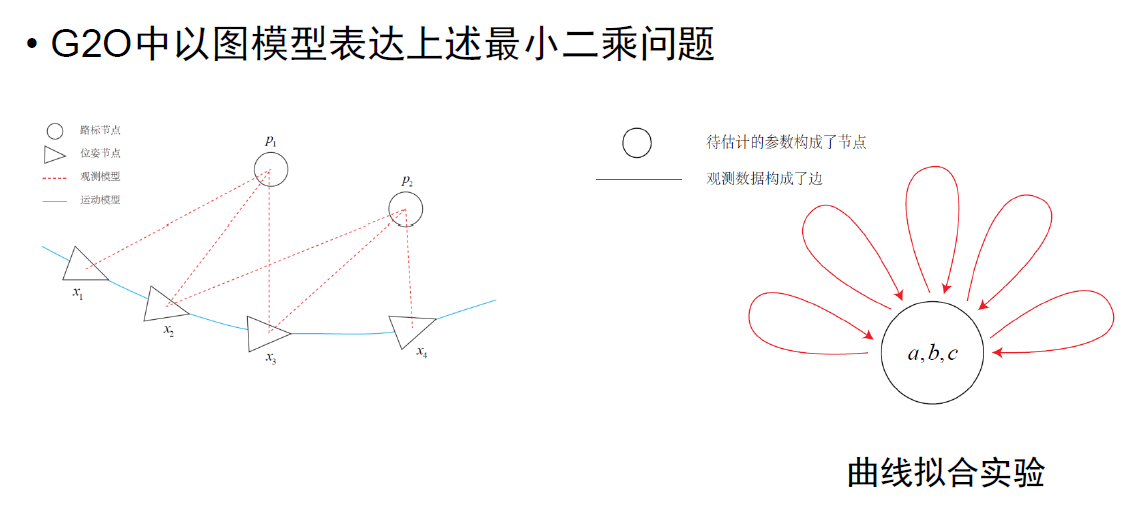
5. 实践：Ceres和g2o