LC 5. 最长回文子串

1. 问题描述

---

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2
输入: "cbbd"
输出: "bb"

Related Topics 字符串 动态规划

2. 题解

---

方法一、中心扩展算法

对于一个子串而言，如果它是回文串，并且长度大于 2，那么将它首尾的两个字母去除之后，它仍然是个回文串。例如对于字符串 “ababa”，如果已经知道 “bab” 是回文串，那么 “ababa” 一定是回文串，这是因为它的首尾两个字母都是 “a”。

用 P(i,j) 表示字符串 s 的第 i 到 j 个字母组成的串，状态转移方程：

思路：枚举所有的「回文中心」并尝试「扩展」，直到无法扩展为止，此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值，即可得到最终的答案。

class Solution {
    public String longestPalindrome(String s) {
        int n = s.length();
        if (s == null || n < 1) {
            return "";
        }
        //分别指向回文串的第一个字母和最后一个字母
        int start = 0, end = 0;
        for(int i=0; i<n; i++){
            int len1 = expandAroundCenter(s, i, i);
            int len2 = expandAroundCenter(s, i, i+1);
            int len = Math.max(len1, len2);
            if(len > end-start+1){
                start = i - (len-1)/2;
                end = i + len/2;
            }
        }
        return s.substring(start, end+1);
    }

    public int expandAroundCenter(String s, int left, int right){
        while(left>=0 && right<s.length() 
            && s.charAt(left)==s.charAt(right)){
            left--;
            right++;
        }
        return right-left-1;
    }
}

复杂度分析

• 时间复杂度：O(n^2)

• 空间复杂度：O(1)

---

方法二、动态规划

用 P(i,j) 表示字符串 s 的第 i 到 j 个字母组成的串，状态转移方程：

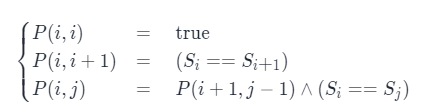
public class Solution {

    public String longestPalindrome(String s) {
        int len = s.length();
        if (len < 2) {
            return s;
        }

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        boolean[][] dp = new boolean[len][len];
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
        }

        char[] charArray = s.toCharArray();
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= len; L++) {
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < len; i++) {
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= len) {
                    break;
                }

                if (charArray[i] != charArray[j]) {
                    dp[i][j] = false;
                } else {
                    //含有2或3个元素时，可以直接返回
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，
                // 此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substring(begin, begin + maxLen);
    }
}

复杂度分析

• 时间复杂度：O(n^2)，其中 n 是字符串的长度。动态规划的状态总数为 O(n^2)，对于每个状态，需要转移的时间为 O(1)。

• 空间复杂度：O(n^2)，即存储动态规划状态需要的空间。

---

方法三、Manacher 算法

复杂度为 O(n) 的 Manacher 算法。然而该算法十分复杂，一般不作为面试内容。

题解