二. 加密算法概述与部分详解

加密，散列算法

2.1 加密算法介绍

2.1.1 对称加密算法

概念

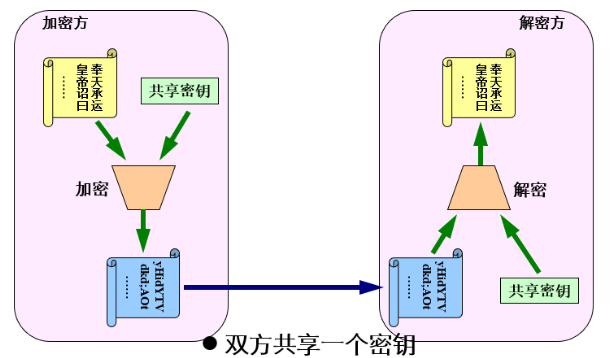
- 发送者和接受者必须使用一个相同的秘钥。
- 通常非常快捷(wire speed)
- 这些算法基于简单的数学运算。
- 对称加密算法实例包括DES、3DES、AES、IDEA、RC2/4/5/6和Blowfish

分组（块）加密和流加密：

分组密码
- 分组密码将固定长度的一组明文数据转换成一组相同长度的密文数据
- 组的长度（块大小）根据算法不同而不同
- 使用填充来让数据尺寸数倍于分组尺寸（块大小）
- 密文通常比明文要长
流密码
- 流密码在更小的明文单位上进行操作，如比特
- 信息尺寸通常不会改变
- 更小的明文单位的转换根据加密时的不同而不同

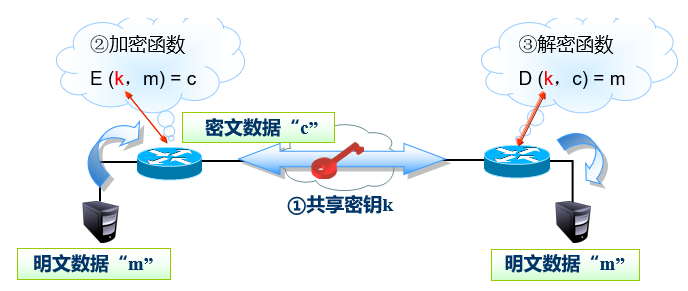
　　图例：

DES概述

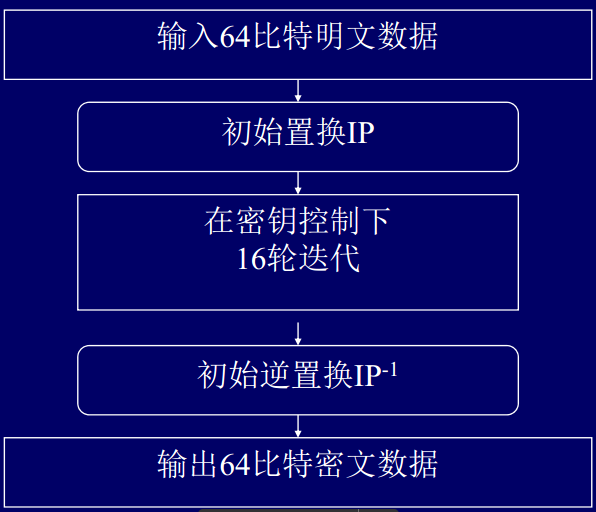
分组加密算法：明文和密文为64位分组长度
§ 对称算法：加密和解密除密钥编排不同外，使用同一算法
§ 密钥长度：56位，但每个第8位为奇偶校验位，可忽略
§ 密钥可为任意的56位数，但存在弱密钥，容易避开
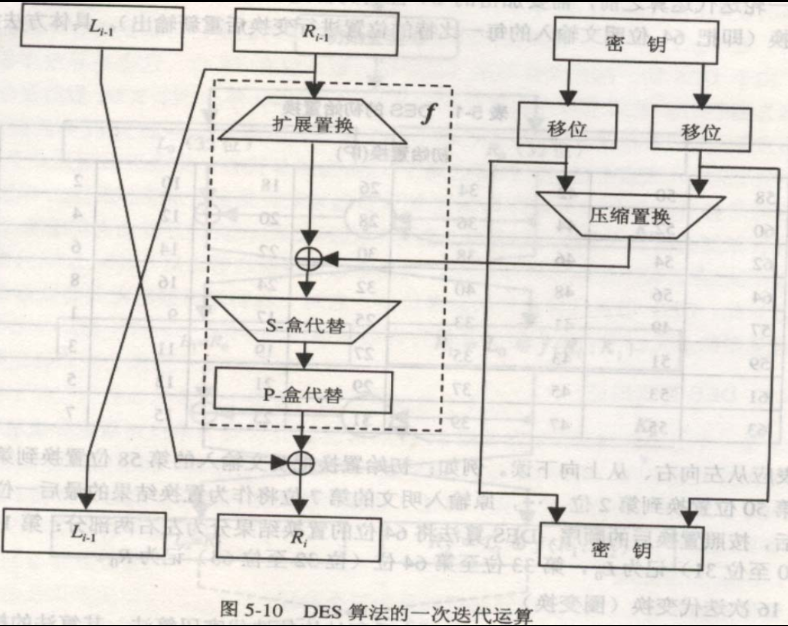
§ 采用混乱和扩散的组合，每个组合先替代后置换，共16轮
§ 只使用了标准的算术和逻辑运算，易于实现

加密过程： 

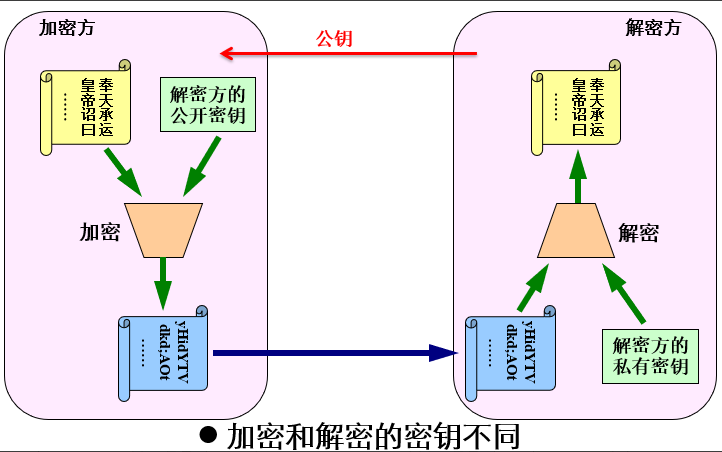
2.1.2 非对称加密算法

概念

- 非对称加密算法亦被称为公钥算法
- 秘钥的一般长度为512 – 4096比特
- 这些算法相对都很慢因为他们基于不同的计算机算法
- 非对称加密算法实例包括RSA、ElGamal、elliptic curves和DH。

核心：通过非对称加密算法加密对称加密算法的密钥；然后再用对称加密算法加密实际要传输的数据。

核心：公钥密码体制基于数学函数（陷门单向函数 ），而单钥密码体制的基础是替代和置换（ 比如：DES等）

单钥加密速度快，适合于加密数据
公钥加密速度慢，但管理简单，适合于数字签名、认证和传递密钥。

　　图例：

　

 　

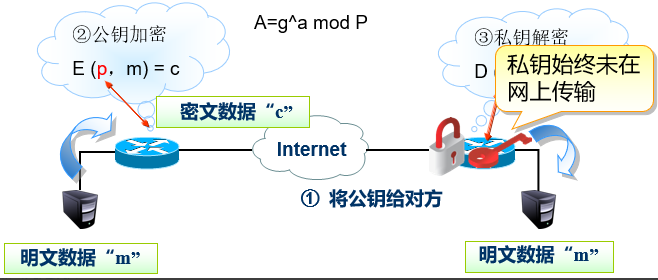
RSA概述

RSA算法的实现
加密
加密消息m时，首先要将明文m分成比n小的数据分组（如果采用二进制数，选取小于n的2的最大次幂），对每一组分别加密

 解密公式为：

若对具体的栗子感兴趣，可以联系我，就不往上放了，格式特别难搞。

对RSA的攻击：

强力攻击（穷举法）：尝试所有可能的私有密钥。
数学分析攻击：各种数学方法，等价与两个素数乘积的因子分解。
其他攻击：对RSA的具体实现存在一些攻击方法，但不是针对基本算法的，而是针对协议的。如选择密文攻击、公共模攻击、低加密指数攻击、低解密指数攻击 。

重点在选择密文攻击。

RSA的诟病：

- RSA涉及到大数的高次幂运算，因此速度较慢，通常用硬件实现，速度大约是DES的1500分之一。
- 因此用RSA加密所有的信息是不现实的，RSA适用于加密的少量数据，如会话密钥和散列值。
- 通常将公钥（ RSA）和单钥（ DES）结合起来会达到更好的效果 。