快递公司送货策略

题目

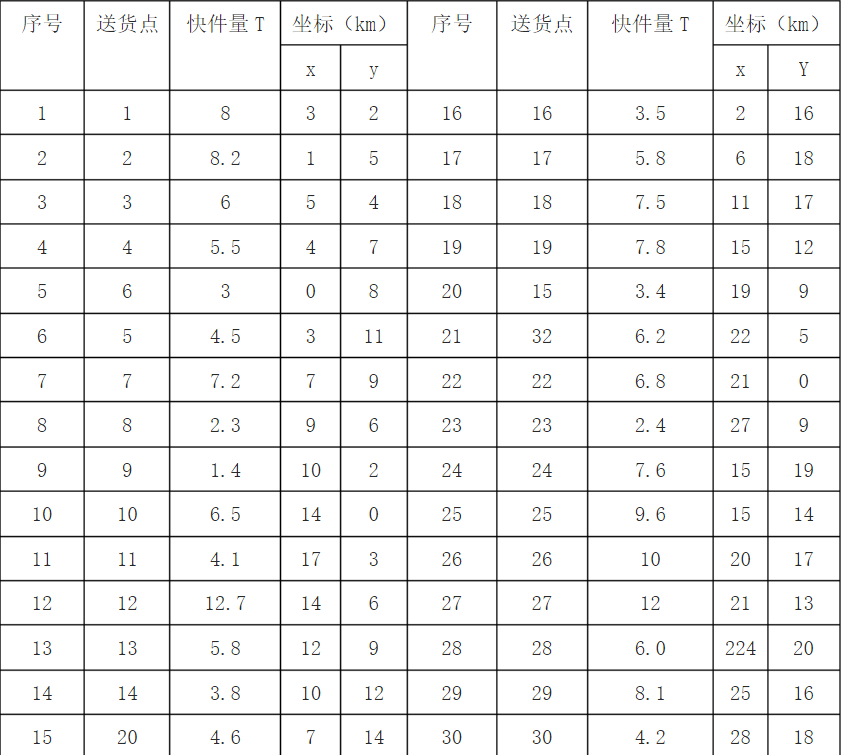
共有30个送货点，由总重量\(7<\frac{184.5}{25}<8\)可知，至少需要8次从总部拿货物。

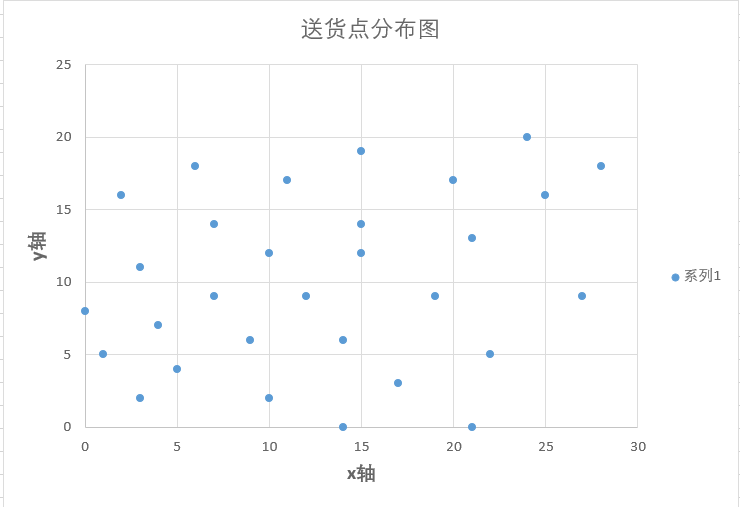
需要将这些送货点分成8个区域，有两个必须达到的要求：

①快件量T<25kg；②时间不超过6小时；

在此基础上，点与点的距离极可能短，

针对问题一，利用单目标0-1规划模型和最佳匹配的原理，将送货点抽象为顶点，由于街道和坐标轴平行，即任意两顶点之间都有路。在此模型中，将两点之间的距离为这两点横纵坐标差的绝对值之和。比如A（xl，y1)，B(x2,y2)两点，则两点之间距离为d=|x2-xl|+ly2-yl|。通过多目标动态规划找出初步路径，再通过lingo软件对各路径进行优化。通过分析，其模型结果为:共需要5名快递员。快递员 1： 0-29-28-30-23-15-0；快递员2： 0-8-26-27-0:快递员3:0-19-24-25-0-1-6-5-2-0;快递员4:0-16-17-18-20-0-3-7-4-0;快递员 5:0-9-11-21-22-10-0-12-13-14-O路程为46lkm，所需总的时间为23.44h。

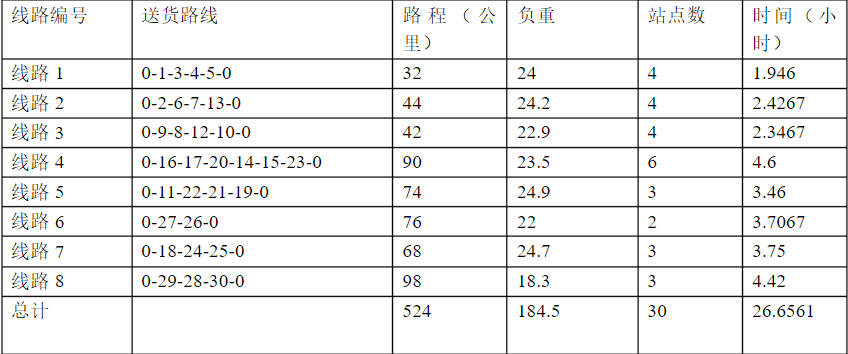
本文学习的是这篇文章，并对代码和一些细节进行了补充，但同时也缺失了一些东西，建议两篇一起阅读。

对于

目标函数：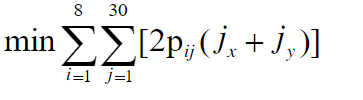

可以看出,当第i条线路都不是最远点时，为最小值，但如果只剩下一个点时，那个便是最远点

用以下代码算出最短的8条线路，问题2，3路线求解

#include<iostream>
#include<fstream>
#include<cmath>
#define M 60 //最远的也没有超过60
using namespace std;
struct node
{
	int x;  //坐标
	int y;
	int num;
	float weight;  //送货点的货物重量
};
node v[31];   //包括原点
int mindis[31];
bool vd[31];
void create(ifstream& in, int n) {  //创建指针in
	int i;
	for (i = 0; i < n; i++) {
		vd[i] = false;
		in >> v[i], num >> v[i].x >> v[i].y >> v[i].weight;    //赋值
		cout << v[i].num << "(" << v[i].x << "," << v[i].y << ")" << v[i].weight << '\t';  //输出
	}
}
int d(node a, node b) {
	return (abs(a.x - b.x) + abs(a.y - b.y));  //距离
}
void dis() {
	int i, j;
	for (i = 0; i < 31; i++) {
		cout << v[i].num << "到各点的距离：\n";
		for (j = 0; j < 31; j++)
			cout << d(v[i], v[j]) << " ";
		cout << endl << endl;
	}
}

计算出离v[0]最近的点

得出

将8小时改成6小时就是第一问的解，然后再用lingo进行优化

model:
sets:
city/1.. 5/:u;
link(city,city):
	dist,
	x;
endsets
n=@size(city);
data:
dist=0 70 115 90 95 ! 距离矩阵;
70 0 46 21 50
115 46 0 30 32
90 21 30 0 48
95 50 32 48 0;
enddata
!目标函数;
min = @sum(link:dist*x);
@FOR(city(K):
!进入城市K;
@sum(city(I)|I #ne# K:x(I,K))=1;
!离开城市K;
@sum(city(J)|J#ne# K:x(K,J))=1;
);
!保证不出现子圈;
@for(city(I)|I #gt# 1:
@for(city(J)|J#gt#1 #and# I #ne# J:
u(I)-u(J)+n*x(I,J)<=n-1);
);
!限制u的范围以加速模型的求解，保证所加的限制并不排除TSP问题的最优解;
@for(city(I)|I #gt# 1: u(I)<=n-2);
!定义X为0\1变量;
@for(link:@bin(x));
End