数学篇
数学
中位数
- 中位数定理:如果有一个数轴,数轴上有若干个点。要在数轴上找一点,使得它到各个点的距离之和最短。
仓库选址
双生双宿之错 - 中位数性质:显然一个奇数组内大于中位数的个数等于小于中位数的个数
- 常规解题思路:利用上述性质,将小于中位数的设置为1,大于等于中位数的设置-1,只要一个区间内的和0,那么就存在这么一个中位数
E1. Submedians (Easy Version):二分答案+利用上述性质
容斥原理
又名抽屉原理:
容斥原理的符号本质是 “修正重复计数”:
计算并集时,“奇加偶减”(集合个数为奇时加,偶时减)
计算并集的补集时,符号反转,表现为 “奇减偶加”
智乃的数字:直接的应用
C. Count Good Numbers
绝对值
求绝对值函数值时,可以考虑拆绝对值
结论
\(max(|x|,|y|)=\frac{|x+y|-|x-y|}{2}\)
位运算
A Good Problem: 奇数时显而易见,全部取l,偶数时取n-2个相同x,2个相同y,找出x&y=0即可,找不出即-1,n=2时需要特判
快速幂
适用于指数较大的情况下
快速加
矩阵快速幂
P1939 矩阵加速(数列):板子题必会
应用:
AcWing 205. 斐波那契:斐波拉契数列的矩阵快速幂
简单题+:计算斐波拉契数列和
广义斐波拉契数列
P1306 斐波那契公约数:优质题解,补充了很多斐波拉契数列的性质及其证明
斐波拉契数列 f(n)=f(n-1)+f(n-2)
\(\begin{bmatrix} f(n) \\ f(n-1) \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{n-1} \begin{bmatrix} f(2) \\ f(1) \end{bmatrix}\)
-
$ \gcd(f_n, f_{n-1}) = 1 $
-
$ f_{m+n} = f_{m+1}f_n + f_m f_{n-1} $
-
$ f_k \mid f_n \iff k \mid n $
奶龙来了 -
$ \gcd(f_n, f_m) = f_{\gcd(n, m)} $
-
\(s(n)=\sum_{1}^{n}f(i)=2*f(n)+f(n-1)-1\)
求前缀和
前缀和数列和原数列由矩阵联系
$\begin{bmatrix} sum_1 \ sum_2 \ sum_3 \ \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 \ 1 & 1 & 0 \ 1 & 1 & 1 \ \end{bmatrix} \begin{bmatrix} a_1\ a_2 \ a_3 \ \end{bmatrix} $
求多次前缀和可用矩阵快速幂
例题:
F. Prefix Sums
进制问题
「LAOI-15」异变危机:思维题,发现对于s,先取10进制转化成s进制,一定成为10,再看成t进制转化成10进制,一定是等于t,基于此思考不可能的情况
两道类似的题
E. Living Sequence:方便理解的题解
还在分糖果!
常见的数学性质
一些性质经常出现在题目中,适当利用就是解题关键
排列
n个数排列代表每个数不重不漏的出现一次,经常出现在题目中
B. Make It Permutation:同时也需要思维,\(i \in [2,n]\),翻转[1,i],然后\(i \in [1,n-1]\),翻转[i+1,n].第一步很好想,因为可以使得第一列全排列,顺着思考,翻转第一排的[2,n],第二列就也是全排列,然后发现这就是规律
MEX
\(MEX a_i\)意味着不超过数组a中最小的数的最大自然数,例如:\(MEX\{2,3,4\}=1\)
一般套路,先考虑\(MEX{a_i}=x\),是否存在x
-
你怎么知道我玩原神还是玩刻晴的?: 考虑是否存在连续的子数组存在1,而此时由于有1,所以gcd也为1,所以只有区间内没有1且gcd为1时才对答案有贡献
异或
线性基
G. Shortest Path Problem?:异或最短路
如果是树则答案唯一——往外走任意路径再走回简单路径答案不变。考虑图比树多什么:往树上加边则形成一个环。根据上方结论,可以任意走到一个环,走完这个环再走简单路径。
于是就显而易见:把每个环的权值加入线性基查询即可。
P4151 [WC2011] 最大XOR和路径
异或是常见考点
E. Adjacent XOR:每个只能异或一次,而\(a_i\)异或的值要么是\(a_{i+1}\)要么是\(b_{i+1}\)
小苯的xor图:对于多个数异或,形如\(a \oplus (b+c+d+....)\),可以转化对应二进制下每位的数量进行异或
性质或结论:
-
\[x \oplus y \oplus z >= x \& y \& z (x,y,z均为非负整数) \]
小苯的序列合并: 关键x ^ y ^ z >= x & y & z
-
\[x + y - (x \oplus y)=2*(x \& y) \]
谁敢动资本的蛋糕:由上述定理,\(s=\sum_{i=1}^{n}a_i\),而每次合并需要\(-cost(x,y)=(x \oplus y)-(x+y)\),最终值为\(sxor=\oplus_{i=1}^{n}a_i\),所以\(ans=s-sxor\)
数论
整除及取余
整除
例题:Subset Multiplication:
$ x $ 一定是 $ b_i / \gcd(b_i, b_{i+1}) $ 的倍数
已知 $ b_i = a_i \cdot x $(被乘 $ x $),需满足原数组的整除性 $ a_i \mid a_{i+1} $。
$ a_{i+1} $ 对应 $ b_{i+1} $
$ b_{i+1} = a_{i+1} $(未被乘 $ x $):
则 $ a_i \mid a_{i+1} \to \frac{b_i}{x} \mid b_{i+1} $,变形为 $ b_i \mid b_{i+1} \cdot x $。
设 $ d = \gcd(b_i, b_{i+1}), b_i = d \cdot m, b_{i+1} = d \cdot n , \gcd(m, n) = 1 $
代入得 $ d \cdot m \mid d \cdot n \cdot x $,约去 $ d $ 后得 $ m \mid n \cdot x $。
由于 $ \gcd(m, n) = 1 $, m 必须整除 x (否则 $ m $ 和 $ n $ 的公共因子会破坏 $ \gcd(m, n) = 1 $ )
而 $ m = \frac{b_i}{d} = \frac{b_i}{\gcd(b_i, b_{i+1})} $,故 $ x $ 必须是 $ \frac{b_i}{\gcd(b_i, b_{i+1})} $ 的倍数。
而对于整个序列,x是所有$ \frac{b_i}{\gcd(b_i, b_{i+1})} $的最小公倍数
D. Price Tags:注意分析时间复杂度,以及运用向上取整的公式
小红的k次方: 整除\(30^k\)其实就是整除\((2*3*5)^k\)
- 小tips
$\lceil \frac{x}{n} \rceil=\frac{x+n-1}{n} $
$\lfloor \frac{x}{n} \rfloor=\frac{x- x \mod n}{n} $
数论分块
取余及同余
倍数关系:
3的倍数满足,所有数相加和为取余为0,9的倍数同理
11的倍数:利用余数之间的关系
小红的好数对
数位关系:
数位之和f(n)=(n-1)%9+1
向下取整,取余:利用取余的性质,将向下取整取余
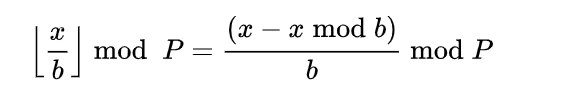
幂中幂plus:由于mod较小,可以找出循环节
赛瓦维斯特定理:已知a,b为大于1的正整数,gcd(a,b)=1,(a,b的最大公约数=1)则使不定方程ax+by=C不存在非负整数解的最大整数(C是最大的 使不定方程 没有 非负整数解 的数。)C=a×b−a−b
得不到的爱情
B. Add 0 or K:令\(a_i+k*c_i\)能被g(g>1)整除,\(g=k+1,c_i=a_i mod (k+1)\)成立
B - Another Divisibility Problem:数论推导
同余
P5656 【模板】二元一次不定方程 (exgcd)
P2613 【模板】有理数取余
练习题:
P1082 [NOIP 2012 提高组] 同余方程
约数
可以由若干个素数相乘得到
-
约数之和:一个数的约数是不同次数的素因子的相乘,由此可以推出解题公式
-
约数个数:一个的约数个数是素因子的次数相乘得到,不同的素因数次数,决定一个不同的因数
同时满足条件的一定是完全平方数,因为题目要求 "因数个数是质数且≠2"。设因数个数为质数p(p≠2),则根据因数个数公式:\((p_1+1)(p_2+1)...(p_n+1)\),p只能是单个因子的乘积(即p = e+1,其中e是某个质因子的指数)。由于p是奇质数(≠2),则e = p-1是偶数,因此原数一定是平方数(e为偶数时,\(p^e = (p^(e/2))²\)
素数
-
素数一定是奇数:B 上海保卫战
-
质因数分解:任意一个整数都可以唯一地分解成多个质因数的乘积
C. Count Good Numbers:分解成小于位数小于的质因数不好,所以只需要找到任取2,3,5,7,组成的最小公倍数
E. Card Game Again:分解k,找满足区间素数个数大于k的各个质因子
立方数:将n质因数分解,因数次数为cnt,\(A×(n的因数)^ {(cnt/3)},B*=cnt%3\),由于我们只要求输出A,所以只需要考虑质因数的四次方不大于n,这样的质因数才会有对A,有贡献 -
欧拉筛
变式:- [蓝桥杯 2022 国 A] 选素数/Primal Sport:在筛素数的同时,记录每个数的最大质因数
- 质数距离:考虑对于任意一个合数 x,他必定存在一个最小的质因子 d
,且这个最小的质因子 $ d<=sqrt(n) $,以此来筛选区间内所有合数
欧拉函数
欧拉函数
\(φ(n)\)的定义:对于正整数\(n,φ(n)\)表示小于等于n且与n互质的正整数的个数
- 定义式(基础)
对正整数\(n\),\(\varphi(n)\)表示\([1,n]\)中与\(n\)互质的正整数的个数,规定:
- 特殊值公式(质数/质数幂,通项推导基础)
- 若\(p\)为质数:\[\boldsymbol{\varphi(p)=p-1} \]
- 若\(p\)为质数,\(k\in\mathbb{N}^*\)(质数幂):\[\boldsymbol{\varphi(p^k)=p^k-p^{k-1}=p^{k-1}(p-1)} \]
- 核心积性公式(欧拉函数核心性质,前提必守)
若正整数\(m,n\)满足\(\boldsymbol{\gcd(m,n)=1}\)(互质),则欧拉函数为积性函数:
注:若\(m,n\)不互质,该公式不成立!
- 通用通项公式(最终核心,素因数分解版)
若\(n\)的标准素因数分解为:\(n=p_1^{k_1}p_2^{k_2}\dots p_r^{k_r}\)(\(p_1,p_2,\dots,p_r\)为\(n\)的不同质因子,\(k_i\geq1\)),则:
关键:仅乘\(n\)的不同质因子,与质因子的幂次无关!
- 常用推论公式(由通项/积性推导,实战高频)
1). 若\(p\)为质数,且\(p\mid n\),则\(\boldsymbol{\varphi(pn)=p\cdot\varphi(n)}\);
2). 若\(p\)为质数,且\(p\nmid n\)(即\(\gcd(p,n)=1\)),则\(\boldsymbol{\varphi(pn)=(p-1)\cdot\varphi(n)}\);
3). 若\(n\)为正偶数,当\(n\)为奇数倍偶数(\(n=2\times\)奇数)时,\(\boldsymbol{\varphi(2n)=\varphi(n)}\);当\(n\)为偶数倍偶数(\(n=2\times\)偶数)时,\(\boldsymbol{\varphi(2n)=2\cdot\varphi(n)}\)。
点击查看代码
ll phi(ll n) {
ll ans = n;
// 1. 单独处理质因子2,便于后续跳过偶数
if (n % 2 == 0) {
ans = ans / 2; // 等价于 ans *= (1 - 1/2)
while (n % 2 == 0) n /= 2;
}
// 2. 从3开始,只检查奇数因子
for (ll i = 3; i * i <= n; i += 2) {
if (n % i == 0) {
ans = ans / i * (i - 1);
while (n % i == 0) n /= i;
}
}
// 3. 处理剩下的最后一个质因子(如果n>1)
if (n > 1) ans = ans / n * (n - 1);
return ans;
}这样效率更高
GCD 与 LCM
前置芝士
\(gcd(a,b)=\gcd(b,a \% b)\)
\(lcm(a,b)=\frac{a \times b}{\gcd(a,b)}\)
LCM补充知识:
- LCM(x, y) 的过程实际上是对 x, y 的每个质因子个数取max的过程。
- 如果 LCM(x, y)!= x,那么如果仅对 y 进行 LCM 操作是无法变成 x 的。
-
简单应用
[蓝桥杯 2023 国 A] 切割:切割成变成正方形,且使得正方形最多,就是找最小公约数,而最小公约数小于最大公约数,枚举因数寻找
小红与gcd和sum:根据gcd的性质,枚举gcd值,从而求出子序列最大值
D. Yet Another Array Problem:思维,最小的使其互质的数一定是质数,否则可以将他分解成质数 -
手推结论
GCD plus LCM,利用上述两个结论就可以很快推出,推不出来看题解
E. Vasya's Function:可以理解为求gcd(x,y),y不断减去gcd(x,y)的次数,暴力求解超时,可以发现y在一定范围内存在相同的gcd(x,y) -
与素数唯一分解定理结合
[蓝桥杯 2024 国 A] gcd 与 lcm:简单的利用上述性质推导之后,需要构造的数组的每个元素由质因数组成.(题解) -
利用互质关系转化
\(gcd(a,b*c)=gcd(a,b)\) if $ gcd(a,c)=1 $ -
求周期
A.小红的数组查询(二)
逆元
零碎知识点:
- \(inv(inv(i))=i\)
组合数
前置知识:
- 求阶乘:用递推f[n]=f[n-1]*i
- 求逆元:因为求组合数时,存在分母取模,而分母是阶乘,所以需要求阶乘逆元.
求组合数
- 公式:\(C_{n}^{m}=\frac{n!}{(n-m)!m!}\)
- 杨辉三角恒等式:\(\dbinom{a}{b} + \dbinom{a}{b-1} = \dbinom{a+1}{b}\)
- 卢卡斯定理:主要用求大组合数取模
- 简单例题:
-伊菲的比赛:简单的推公式,高中问题
隔板法求不定方程
范德蒙德恒等式
\(C_{n+m}^{k}=\sum_{i=0}^{k}C_{n}^{i} * C_{m}^{k-i}\)
F - 1122 Subsequence 2
多重组合数
多重组合数(也称为多重排列数)是组合数学中用于计算有重复元素的排列方式数的概念。
假设有 $ k $ 种“类型”的元素,第 $ i $ 种类型有 $ n_i $ 个完全相同的元素。将所有元素(总共有 $ n = n_1 + n_2 + \dots + n_k $ 个)排成一列,这样的排列方式总数就是多重组合数。
计算公式
多重组合数的公式为:
其中:
- $ n = n_1 + n_2 + \dots + n_k $(总元素数);
- $ n_i! $ 是第 $ i $ 种类型元素的“内部重复数”(因为相同元素的排列会被视为重复,需要除去)。
k部分拆分数
构造序列:简单例题
期望
J - Points on the Number Axis A:期望位置 = 所有初始点的平均值,[题解]
几何分布
(https://codeforces.com/gym/105139/attachments/download/25287/Sol_ICPC_hubei_24.pdf)
擅长解密的小红同学
确定密码的总长度和排列数
设每个数字0-9出现的次数为$ a_0, a_1, \dots, a_9 ,密码的总长度为 n = a_0 + a_1 + \dots + a_9 $。
由于密码是这些数字的一个排列(顺序不同则密码不同),所以总共有$ \frac{n!}{a_0! \cdot a_1! \cdot \dots \cdot a_9!} $种不同的有效密码**(这是多重排列的计算公式,分母是各数字出现次数的阶乘之积,用于消除重复数字的排列冗余)。
分析尝试次数的期望
每次尝试成功的概率是“当前尝试恰好是正确密码”的概率。由于每次尝试后密码重置,且所有可能的密码是等概率被尝试的,因此这是一个几何分布问题。
对于几何分布,“首次成功的期望次数”等于“成功概率的倒数”。这里成功概率$ p = \frac{1}{\text{总排列数}} $,因此期望尝试次数为:
博弈论
必胜态(N-position, Next player win):
当前轮到行动的玩家有必胜策略的状态;无论对手如何应对,都能最终获胜;至少存在一种合法操作,使对手陷入必败态
必败态(P-position, Previous player win):
当前轮到行动的玩家无论怎么走都必输的状态;所有合法操作都会让对手进入必胜态;没有操作可以迫使对手进入必败态
取石子游戏
规则
有 1 堆石子,共 n 个;
两人交替取,每次至少取 1 个,最多取 m 个;
最后取完石子的人获胜
必败态:当 n % (m+1) == 0 时,当前玩家必败(无论取 k 个,对手都能取 m+1 -k 个,最终对手取完)。
必胜态:当 n % (m+1) != 0 时,当前玩家必胜(先取 n % (m+1) 个石子,让剩余石子数为 m+1 的倍数,迫使对手进入必败态)
- 例题I Wanna Win the Cards:每次取至少一个,之多k个不为种植不为1的数
- 取石子游戏plus:好的题解
- DP或递推:
照天地苍茫,却有花影成双:1,2,3的情况确定,于是可以一个一个推出大于3的情况,那么对于第i个,如果减去所有的小于的i的平方数都无法胜利,那么就失败
D - The Simple Game :在这种博弈论任务中,从最终状态回溯获胜者通常很有效 - 搜索
Games may be harmful:记忆化搜索的时间复杂度是足够的,根据博弈关系搜索
点击查看代码
#include <bits/stdc++.h>
using namespace std;
// 记忆化存储:键为当前状态(a, b)(桃血量a,敌人血量b),值为博弈结果
// 结果定义:0=桃败,1=循环,2=桃胜
map<pair<long long, long long>, int> memo;
/**
* @brief 递归判断当前血量状态(a, b)下桃的最终结果
* @param a 桃当前的血量
* @param b 敌人当前的血量
* @return int 0=桃败,1=循环,2=桃胜
*/
int dfs(long long a, long long b) {
// 特殊状态:(1,1)经推导必为循环态(双方无法让对方血量归0,无限循环)
if (a == 1 && b == 1) {
return 1;
}
// 构造当前状态的键,检查是否已计算过,避免重复递归
auto state = make_pair(a, b);
if (memo.count(state)) {
return memo[state];
}
// tr[0]:桃选择“加血”后的最终结果;tr[1]:桃选择“跳过”后的最终结果
int tr[2];
// 循环枚举桃的两种行动:i=0→加血(a+1),i=1→跳过(a不变)
for (int i = 0; i < 2; i++) {
long long a1 = a + i; // 桃行动后的血量(i=0加1,i=1不变)
// er[0]:敌人应对“加血”后的结果;er[1]:敌人应对“跳过”后的结果
int er[2];
// 循环枚举敌人的两种应对:j=0→加血(b+1),j=1→跳过(b不变)
for (int j = 0; j < 2; j++) {
long long b1 = b + j; // 敌人应对后的血量(j=0加1,j=1不变)
// 结算阶段:1.交换血量 2.向下取半(a_new=敌人行动后血量//2,b_new=桃行动后血量//2)
long long a_new = b1 / 2; // 桃结算后的新血量
long long b_new = a1 / 2; // 敌人结算后的新血量
int res; // 当前应对方式下的结果
if (a_new == 0 && b_new == 0) {
// 双方结算后血量均为0,按规则补1血,进入(1,1)状态
res = dfs(1, 1);
} else if (b_new == 0) {
// 敌人结算后血量为0→桃胜
res = 2;
} else if (a_new == 0) {
// 桃结算后血量为0→桃败
res = 0;
} else {
// 双方血量均不为0,递归判断新状态(a_new, b_new)
res = dfs(a_new, b_new);
}
er[j] = res; // 记录敌人当前应对的结果
}
// 敌人会选择对桃“最不利”的结果(取两种应对的最小值)
tr[i] = min(er[0], er[1]);
}
// 桃会选择对自己“最有利”的结果(取两种行动的最大值)
// 存入记忆化缓存,避免后续重复计算
memo[state] = max(tr[0], tr[1]);
return memo[state];
}
int main() {
int T; // 测试用例数量
cin >> T;
// 桃败时需要输出的固定字符串(题目给定,不可修改)
string lose_str = ")YRU380ilgpbfpiUkrhr89fH*RT#QYU(_&U*)$ Q@&#!@*)R";
// 处理每组测试用例
while (T--) {
long long a, b; // 每组用例的初始血量(桃a,敌人b)
cin >> a >> b;
// 清空记忆化缓存:避免上一组用例的状态干扰当前组
memo.clear();
// 获取当前初始状态的博弈结果
int result = dfs(a, b);
// 根据结果输出对应内容
if (result == 2) {
cout << "EZ GAME\n"; // 桃胜
} else if (result == 0) {
cout << lose_str << '\n'; // 桃败
} else {
cout << "KUYASHI---!!!\n"; // 循环
}
}
return 0;
}
-
博弈反推
小红拿石子2.0:从最终态反推启发思考 -
思考
D. Game on Array: 可以考虑对单独一个数 -
归纳
2024 Jiangsu Collegiate Programming Contest:K. Number Deletion Game:极大值的奇偶性决定次大值的奇偶性,决定最终的winner
计算几何
三角形
小红的整数三角形:三角形面积公式∣(x2−x1)(y3−y1)−(x3−x1)(y2−y1)|/2
距离
曼哈顿距离:\(|x_1-x_2|+|y_1-y_2|\)
欧式距离: \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)
D 距离之比:利用三角换元
极角排序
利用叉积排序,避免精度误差
E - Laser Takahashi
凹包和凸包
凸多边形:所有顶点的 “转向” 方向完全一致(要么全逆时针,要么全顺时针)。
凹多边形:至少存在一个顶点的 “转向” 方向与其他顶点相反(即存在凹角)
凹包
逆时针遍历三个点l,i,r,向量分别为b(l->i),c(i->r),利用叉积判断转向,若值全部为正或者负,为凸多边形,存在不同的即为凹多边形
对应习题:
凹包
凸包
严格凸的核心条件是:任意边长度 < 其余边长度和
C. Symmetrical Polygons:偶数次必拿,奇数次木棒考虑拿一个还是拿两个,需要满足上述条件



 浙公网安备 33010602011771号
浙公网安备 33010602011771号