算法学习总结(二)：选择排序

一、算法简介

      每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法。

二、算法描述

　　n个记录的文件的直接选择排序可经过n-1趟直接选择排序得到有序结果：

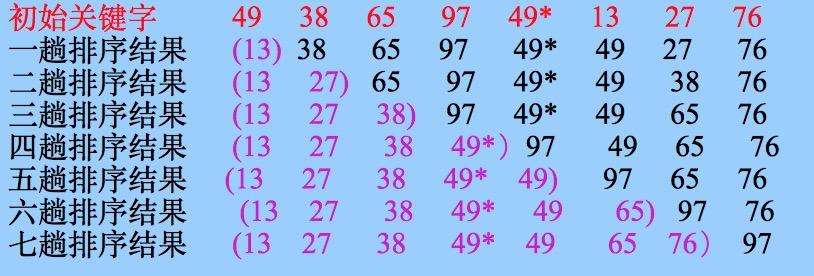
       1、初始状态：无序区为R[1..n]，有序区为空。

       2、第i趟排序(i=1,2,3...n-1)

　　第i趟排序开始时，当前有序区和无序区分别为R[1..i-1]和R(i..n）。该趟排序从当前无序区中选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1..i]和R分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区。

       3、前n-1趟结束，数组有序化了

      选择排序的交换操作介于0和(n-1)次之间。选择排序的比较操作为n(n-1)/2次之间。选择排序的赋值操作介于0和3(n-1)次之间。比较次数O(n^2),比较次数与关键字的初始状态无关，总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2。 交换次数O(n),最好情况是，已经有序，交换0次；最坏情况是，逆序，交换n-1次。 交换次数比冒泡排序少多了，由于交换所需CPU时间比比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。

最差时间复杂度	O(n^2)
最优时间复杂度	O(n^2)
平均时间复杂度	O(n^2)
最差空间复杂度	总共O(n)，需要辅助空间O(1)

 

三、算法图解

四、示例代码

 public class SelectSort {
        //选择排序

	public static void selectSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int mini = 0;
		for (int i = 0; i < arr.length - 1; i++) {
			mini = i;
			for (int j = i + 1; j < arr.length; j++) {
				mini = arr[mini] > arr[j] ? j : mini;
			}
			swap(arr, i, mini);
		}
	}
        //交换两个元素的顺序
	public static void swap(int[] arr, int index1, int index2) {
		int tmp = arr[index1];
		arr[index1] = arr[index2];
		arr[index2] = tmp;
	}
}