hdu 4406费用流神奇的建图

题意：再有n天就考试了， 如果不复习的话那么每门科目只能得到一点基础的分， 现在每天能复习k节课，每节课能让这门功课涨一分，但是每天能复习的科目是固定定的。现在也知道每门课的学分， 一直GPA的公式是这样计算的。现在想让GPA尽量的高， 并且保证不挂科， 现在问最高的gpa是多少？ 如果挂科了输出0。

，       

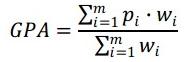
思路： 这道题开始的时候想到了用网络流，但是由于这个东西不是累计的， 所以没有想出来如何建图。后来看了别人的报告， 当不能累计的时候可以构造累计， 比如上一个是a[i], 那么我的下一个是a[i+1]-a[i]，就可以累计了。 由于这个p是离散化的， 并且数目也较小。这个问题就是这样解决的，  我们就是这样对于x计算出来的值为m[i],

我们的费用直接用m[i] - m[i-1], m[i+1]-m[i].......，只要保证如果有流的话先流前边的就行，最后就相当于只流了最后（当然要对第一项修正）。 还有就是对于一定要满足都及格，可以这样处理， 如果score[i]<60,可以建一条

流量为60-score[i]的边，费用是负无穷（这样能保证会先流这个边）， 同样最后一定要把这个值修正过来。

还有就是这道题可以都用整数， 过程中只用(100-x)*(100-x)*w[i],最后再把其他的常数加上。

AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <queue>
#include <vector>
#include <map>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 300, M = 30100;
const LL INF = 1LL<<45;

struct EDGE
{
    int u, v, cap, next;
    LL w;
} edge[M];

int n, k, m, num, head[N];
int w[N], s[N], cc, f[N], pre[N];
LL d[N], tp;

void getf()
{
    for(int i=60; i<=100; i++)
    {
        f[i] = (100-i)*(100-i);
    }
}

void add(int u, int v, int cap, LL w)
{
    edge[num].u = u;
    edge[num].v = v;
    edge[num].cap = cap;
    edge[num].w = w;
    edge[num].next = head[u];
    head[u] = num++;
}

void init()
{
    num = 0;
    memset(head, -1, sizeof(head));
    for(int i=1; i<=m; i++)
    {
        scanf("%d", &w[i]);
    }

    int t=n+m+1;
    cc = 0;
    tp = 0;
    for (int i=1; i<=m; i++)
    {
        scanf("%d", &s[i]);
        if(s[i] < 60)
        {
            cc += (60-s[i]);
            add(n+i, t, 60-s[i], -INF);
            add(t, n+i, 0, INF);
            tp += f[60]*w[i];
        }
        else
        {
            tp += f[s[i]]*w[i];
        }
        for (int j=max(61,s[i]+1); j<101; j++)
        {
            add(n+i, t, 1, (f[j]-f[j-1])*w[i] );
            add(t, n+i, 0, (-f[j]+f[j-1])*w[i] );
        }
    }

    for(int i=1; i<=n; i++)
    {
        add(0, i, k, 0);
        add(i, 0, 0, 0);
    }

    int a;
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            scanf("%d", &a);
            if(a)
            {
                add(i, n+j, 10000, 0);
                add(n+j, i, 0, 0);
            }
        }
    }
}

bool SPFA(int s,int t)
{
    int u, v;
    LL w;
    bool in[N] = {0};
    for(int i  = 0; i <= t; i++)
        d[i] = INF*1000;
    memset(pre,-1,sizeof(pre));
    queue<int>q;
    in[s] = 1;
    d[s] = 0;
    q.push(s);
    while(! q.empty())
    {
        u = q.front();
        q.pop();
        in[u] = 0;
        for(int i = head[u]; i != -1; i = edge[i].next)
        {
            if(edge[i].cap <= 0) continue;
            v = edge[i].v;
            w = edge[i].w;
            if(d[v] > d[u] + w)
            {
                pre[v] = i;
                d[v] = d[u] + w;
                if(!in[v])
                {
                    in[v]  = 1;
                    q.push(v);
                }
            }
        }
    }
    return d[t] <= INF*500;
}

LL EK(int s,int t)
{
    int temp = 1000000;
    int ptr = pre[t];
    while(ptr != -1)
    {
        temp = min(temp,edge[ptr].cap);
        ptr = pre[edge[ptr].u];
    }
    ptr = pre[t];
    while(ptr != - 1)
    {
        edge[ptr].cap -= temp;
        edge[ptr^1].cap += temp;
        ptr = pre[edge[ptr].u];
    }
    return d[t]*temp;
}

void solve()
{
    LL ans = 0;
    while(SPFA(0,n+m+1))
    {
        ans += EK(0,n+m+1);
    }
    ans += tp;
    ans += cc*INF;
    int sum = 0;
    for(int i=1; i<=m; i++)
     sum += w[i];
    double ans1 = 4-ans*3.0/1600/sum;
    if(ans1 <= 0)
     printf("0.000000\n");
    else printf("%.6f\n", ans1);
}

int main()
{
    getf();
    while(scanf("%d%d%d", &n, &k, &m) != EOF)
    {
        if(n==0 && k==0 && m==0)
         break;
        init();
        solve();
    }
    return 0;
}