P2181 Diagonal

Description

If there is a convex polygon with n vertices, None of its three diagonals intersect at one point. Please compute the diagonals intersect points of the polygon?

For example, hexagon：

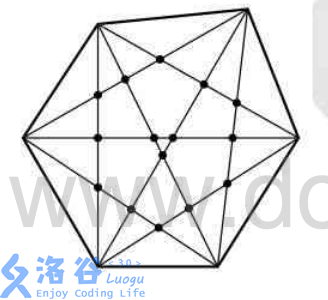
Input

Only one line and a single number n represent the number of edges.

Output

Only one line and a number represent the answer.

Input and output example

input
3
output
0

input
6
output
15

notice

For half of the data, 3<=n<=100.
For the whole data, 3<=n<=10^5.

！！！！！！！！！！！！！！！！！！！！！！！

Code

#include <iostream>
using namespace std;

int diagonal() {
    unsigned long long p;
    cin >> p;
    cout << p*(p-1)/2*(p-2)/3*(p-3)/4;
    return 0;
}

What I learned

On the content said two diagonals will cross on a point. So we can see a rectangle consisted of four vertexes that include the two diagonals.

Then, we change the problem to find the combination of any four vertices, and changing the order will not change the diagonal, so we need the combination divided by 4.

Finally we get the formula: n * (n-1) * (n-2) * (n-3) / 24

Meanwhile, we need to consider the size of the data. For preventing oversize, we simplify the formula to n * (n-1) / 2 * (n-2) / 3 * (n-3) / 4

Will not this simplification cause Round down? The answer is no, as a matter of fact, it can be divided completely. First, there must be a multiple of 2 between in n and n-1. Second, there is a number in n,n-1,n-2 can be divided completely by 3, etc.