Binary tree

"Abstract:" In computer science, a binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.

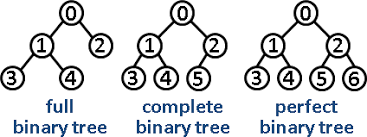
Strictly binary tree(more strict than the common binary tree, as called Full Binary Tree)

There is another definition related to the binary tree, Strictly binary tree, it's rooted too, but every node has 0 or 2 child nodes, and the level of nodes doesn't matter in the strict binary tree. In short, The full binary tree, where every node other than the leaves has two children.

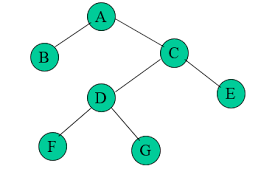
Complete binary tree

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

As for the properties of binary trees

e.g.: The number of nodes \(n\) in a full binary tree, is at least \(n=2h+1\) and at most \(n=2^{h+1}-1\), where \(h\) is the height of the tree. A tree consisting of only a root node has a height of 0. It will be easy to infer after you understand its definition.

Application in computing

• First, as a means of accessing nodes based on some value or label associated with each node. Binary trees labeled this way are used to implement binary search trees and binary heaps, and are used for efficient searching and sorting.
• Second, as a representation of data with a relevant bifurcating structure. In such cases, the particular arrangement of nodes under and/or to the left or right of other nodes is part of the information (that is, changing it would change the meaning). Common examples occur with Huffman coding and cladograms. The everyday division of documents into chapters, sections, paragraphs, and so on is an analogous example with n-ary rather than binary trees.
  Copied from https://en.wikipedia.org/wiki/Binary_tree

Tree traversal(Highly recommend that you simulate a recursively call when you are finding orders)

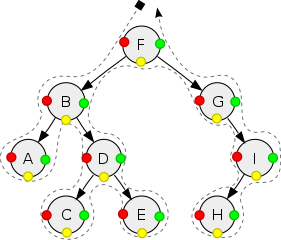
Pre-order(root-left-right order to recursively call)

1. Access the data part of the current node
2. Traverse the left subtree by recursively calling the pre-order function
3. Traverse the right subtree by recursively calling the pre-order function

pre-order(red): F, B, A, D, C, E, G, I, H

In-order(left-root-right order to recursively call)

1. Traverse the left subtree by recursively calling the in-order function
2. Access the data part of the current node
3. Traverse the right subtree by recursively calling the in-order function

in-order(yellow): A, B, C, D, E, F, G, H, I

Post-order(left-right-root order to recursively call)

1. Traverse the left subtree by recursively calling the post-order function
2. Traverse the right subtree by recursively calling the post-order function
3. Access the data part of the current node

post-order(green): A, C, E, D, B, H, I, G, F

Under knowing pre-order and in-order, write post-order

#include <iostream>
#include <cstring>
#define MAX 50
using namespace std;
typedef char Elem_Type;
typedef struct BiTree
{
	Elem_Type data;
	struct BiTree *Lchild;
	struct BiTree *Rchild;
}BiTree;

int Search_Num(Elem_Type num, Elem_Type *array, int len)
{
	for (int i = 0; i<len; i++)
	if (array[i] == num)
	return i;
}

BiTree *Resume_BiTree(Elem_Type *pre, Elem_Type *center, int len){
	if(len <= 0)
	return NULL;
	BiTree *temp = new BiTree;
	temp->data = pre[0];
	int index = Search_Num(temp->data, center, len);
	temp->Lchild = Resume_BiTree(pre+1, center, index); 
	temp->Rchild = Resume_BiTree(pre+1+index, center+index+1, len-index-1);
    return temp;
}

void PostOrderTraverse(BiTree *root)
{
    if (root != NULL)
    {
        
        PostOrderTraverse(root->Lchild);
        PostOrderTraverse(root->Rchild);
        cout << root->data;
    }
}

int main(void){
	Elem_Type *preorder = new Elem_Type[MAX];
	Elem_Type *inorder = new Elem_Type[MAX];
	cout<<"input pre-order traversal: "<<endl;
	cin >> preorder; 
	cout<<"input in-order traversal: "<<endl;
	cin >> inorder;
	BiTree *root = Resume_BiTree(preorder, inorder, strlen(inorder));
	cout <<"post-order traversal is: "<<endl;
	PostOrderTraverse(root);
	cout << endl;
	delete[] preorder;
	delete[] inorder;
	return 0;
}

Under knowing in-order and post-order, write pre-order

#include <iostream>
#include <cstring>
#define MAX 50
using namespace std;
typedef char Elem_Type;
typedef struct BiTree
{
	Elem_Type data;
	struct BiTree *Lchild;
	struct BiTree *Rchild;
}BiTree;

int Search_Num(Elem_Type num, Elem_Type *array, int len)
{
	for(int i=0; i<len; i++)
	{
		if(array[i]==num)
		return i;
	}
}

BiTree *Resume_BiTree(Elem_Type *post, Elem_Type *center, int len){
	if(len<=0) return NULL;
	BiTree *temp = new BiTree;
	temp->data = post[len - 1];
	int index = Search_Num(temp->data, center, len);
	temp->Lchild = Resume_BiTree(post, center, index);
	temp->Rchild = Resume_BiTree(post + index, center + index + 1, len - index - 1);
    return temp;
}

void PreOrderTraverse(BiTree *root){
	if(root!=NULL)
	{
		cout<<root->data;
		PreOrderTraverse(root->Lchild);
		PreOrderTraverse(root->Rchild);
	}
}

int main(void){
	Elem_Type *inorder = new Elem_Type[MAX];
	Elem_Type *postorder = new Elem_Type[MAX];
	cout<<"input post-order traversal: "<<endl; 
	cin >> postorder;
	cout<<"input in-order traversal: "<<endl; 
	cin >> inorder;
	BiTree * root = Resume_BiTree(postorder, inorder, strlen(inorder));
	cout<<"pre-order traversal is: "<<endl; 
	PreOrderTraverse(root);
	cout << endl;
	delete[] inorder;
	delete[] postorder;
	return 0;
}

Huffman coding

from heapq import heappush, heappop, heapify
from collections import defaultdict
from bitarray import bitarray

padding_len = 0

def freq(text):
    freq_lib = defaultdict(int)
    for ch in text:
        freq_lib[ch] += 1
    return freq_lib

def huffman(text):
    text = freq(text)
    heap = [[count, [sym, ""]] for sym, count in text.items() ]
    
    heapify(heap)

    #pritn(heap)

    while(len(heap)>1):
        right = heappop(heap)
        print('right = ', right)
        left = heappop(heap)
        print('left = ', left)

        for pair in right[1:]:
            print(pair[1])
            pair[1] = '0'+pair[1]
        print('right add zero = ', right)
        for pair in left[1:]:
            pair[1] = '1'+pair[1]
        print('left add one = ', left)
        print('')
        heappush(heap, [right[0]+left[0]]+right[1:]+left[1:])

    huffman_list = right[1:] + left[1:]
    #print(huffman_list)
    huffman_dict = {a[0]:bitarray(str(a[1])) for a in huffman_list}
    return huffman_dict

def encoding(dict, text):
    encoded_text = bitarray()
    encoded_text.encode(dict,text)
    global padding_len
    padding_len = padding(len(encoded_text))
    return encoded_text+str('0'*padding_len)

def padding(length):
    strlen = length%8
    if strlen !=0 :
        padding = 8 - strlen
        return padding
    return 0

def decoding(dict, encoding):
    decoded_text = bitarray()

    global padding_len

    if padding_len == 0:
        decoded_text = encoding
    else:
        decoded_text = encoding[:-padding_len]
    decoded_text = decoded_text.decode(dict)
    decoded_text = ''.join(decoded_text)
    return decoded_text


if __name__ == '__main__':
    text = input("input the txt that you want to encode: ")
    huff = huffman(text)
    encoding = encoding(huff, text)
    print("encoded: "+str(encoding))
    decoding = decoding(huff, encoding)
    print("decoded: "+str(decoding))