【机器学习实战】-- Titanic 数据集（1）-- 朴素贝叶斯

1. 写在前面: 

本篇属于实战部分，更注重于算法在实际项目中的应用。如需对朴素贝叶斯算法本身有进一步的了解，可参考以下链接，在本人学习的过程中，起到了很大的帮助：

统计学习方法 李航

朴素贝叶斯算法原理小结 https://www/cnblogs.com/pinard/p/6069267.html

极大似然估计法推出朴素贝叶斯法中的先验概率估计公式？https://www.zhihu.com/question/33959624

 

2. 数据集：

数据集地址：https://www.kaggle.com/c/titanic

Titanic数据集是Kaggle上参与人数最多的项目之一。数据本身简单小巧，适合初学者上手，深入了解比较各个机器学习算法。

数据集包含11个变量：PassengerID、Pclass、Name、Sex、Age、SibSp、Parch、Ticket、Fare、Cabin、Embarked，通过这些数据来预测乘客在Titanic事故中是否幸存下来。

 

3. 算法简介： 

朴素贝叶斯算法是基于贝叶斯定理与特征条件独立性假设的分类方法，是少有的生成模型。

3.1 朴素贝叶斯模型：

设输入空间$\chi \subseteq  \textbf{R}^{n}$，输出空间$\Upsilon = \left \{ c_{1}, c_{2}, ..., c_{K} \right \}$，并给定训练数据集，其中$x \in \chi$, $y \in \Upsilon$：

$$ T = \left \{ \left ( x_{1}, y_{1} \right ), \left ( x_{2}, y_{2} \right ), ..., \left ( x_{N}, y_{N} \right ) \right \} $$

首先，我们通过训练数据集学习先验概率以及条件概率分布：

先验概率：

$$ P(Y=c_{k}), \quad k=1,2,...,K $$

条件概率：

$$ P(X = x | Y=c_{k}) = P(X^{(1)} = x^{(1)},X^{(2)} = x^{(2)} ..., X^{(n)} = x^{(n)}|Y=c_{k}), \quad k=1,2,...,K $$

其次，由于条件概率中的参数是指数级别的，没有办法学习这么多的参数。因此，，朴素贝叶斯法在此应用了条件独立性假设，该假设假定用于分类的n个特征在类确定的条件下都是条件独立的：

$$ P(X = x | Y=c_{k}) = P(X^{(1)} = x^{(1)},X^{(2)} = x^{(2)} ..., X^{(n)} = x^{(n)}|Y=c_{k}) = \prod_{j=1}^{n} P(X^{j} = x^{j} | Y = c_{k}) $$

3.2  朴素贝叶斯的参数估计：

由于朴素贝叶斯是生成模型，并没有损失函数，其学习的过程就是基于训练数据，对先验概率和条件概率这两个参数进行估计。

首先，对于输入空间中的样本$X$，我们可以根据其不同的数据类型，假设其符合某一分布，常见的分布包括：伯努利分布（样本数据分布系数）、多项式分布（样本数据离散）、正态分布（样本数据离散）。

 其次，假设完样本分布之后，通过极大似然估计来获取先验概率和条件概率的估计值。这里，我们以多项式分布为例，且假设输入空间是一维的：$(x_{1}, y_{1})$, $(x_{2}, y_{2})$, ..., $(x_{n}, y_{n})$

假设$\mu _{lk} = P(x=a_{l}|y=c_{k})$, $\theta_{k} = P(y=c_{k})$，是极大似然法要估计的参数。

似然函数：

$$ L\left ( \left ( \mu_{lk}, \theta_{k} \right ); (x_{1}, y_{1}), (x_{2}, y_{2}), ..., (x_{n}, y_{n})\right ) = \prod _{i=1}^{n} P(x_{i}, y_{i}) = \prod_{l=1}^{L} \prod_{k=1}^{K}(\mu_{lk} \cdot \theta_{k})^{N_{lk}} $$

对数似然函数：

$$ l\left ( \left ( \mu_{lk}, \theta_{k} \right ); (x_{1}, y_{1}), (x_{2}, y_{2}), ..., (x_{n}, y_{n})\right ) = \sum_{l=1}^{L} \sum_{k=1}^{K}N_{lk}(ln\mu_{lk} + ln\theta_{k}) \quad \text{s.t.} \quad  \sum_{l=1}^{L} \mu_{lk} = 1 , \quad \sum_{k=1}^{K} \theta_{k} = 1$$

利用拉格朗日乘子法可以得到：

$$ F(\mu, \theta, \lambda_{1}, \lambda_{2}) =   \sum_{l=1}^{L} \sum_{k=1}^{K}N_{lk}(ln\mu_{lk} + ln\theta_{k}) + \lambda_{1}(\mu_{lk} - 1) + \lambda_{2}(\theta_{k} - 1)$$ 

 对参数$\mu$求导可得：

$$ \frac{\partial F}{\partial \mu} = \frac{N_{lk}}{\mu_{lk}} + \lambda_{1} = 0 $$

$$ \mu_{lk} = -\frac{N_{lk}}{\lambda_{1}} \quad \rightarrow \quad  \sum_{l=1}^{L}(-\frac{N_{lk}}{\lambda_{1}}) =1 \quad \rightarrow \quad \lambda_{1} = -N_{k}  $$

$$ \mu_{lk} = \frac{N_{lk}}{N_{k}} $$

 

 对参数$\theta$求导可得：

$$ \frac{\partial F}{\partial \theta}  = \sum_{l=1}^{L} \frac{N_{lk}}{\theta_{k}} + \lambda_{2} = 0$$

$$ \theta_{k} = -\frac{\sum_{l=1}^{L} N_{lk}}{\lambda_{2}}  \quad \rightarrow \quad \sum_{k=1}^{K} (-\frac{N_{k}}{\lambda_{2}}) = 1 \quad \rightarrow \quad \lambda_{2} = -N$$

$$ \theta_{k} = \frac{N_{k}}{N} $$

 

4. 实战：

实战过程包括特征选取、数据清洗、模型选择、以及结果分析。

首先导入数据，以及各类所需的包，包括sklearn, pandas, numpy。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline, FeatureUnion
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import LabelEncoder, OneHotEncoder, LabelBinarizer, OrdinalEncoder
from sklearn.naive_bayes import MultinomialNB, ComplementNB, GaussianNB
from sklearn.metrics import accuracy_score, f1_score, roc_auc_score, precision_score, recall_score
from sklearn.base import TransformerMixin, BaseEstimator


class MyLabelBinarizer(TransformerMixin):
    def __init__(self, *args, **kwargs):
        self.encoder = LabelBinarizer(*args, **kwargs)

    def fit(self, x, y=0):
        self.encoder.fit(x)
        return self

    def transform(self, x, y=0):
        return self.encoder.transform(x)


class DataFrameSelector(BaseEstimator, TransformerMixin):
    def __init__(self, attribute_name):
        self.attribute_name = attribute_name

    def fit(self, x, y=None):
        return self

    def transform(self, x):
        return x[self.attribute_name].values


data_train = pd.read_csv('train.csv')

train_x = data_train.drop('Survived', axis=1)
train_y = data_train['Survived']

 

其次，以上还定义了两个类，MyLabelBinarizer 和 DataFrameSelector。 看过《Hands-ON Machine Learning with Scikit-Learn & Tensorflow》的各位，应该会对两个类有印象，后续用到时将会进一步提到。

 

 4.1 特征选取

 首先，先简要看一下train_x。

 

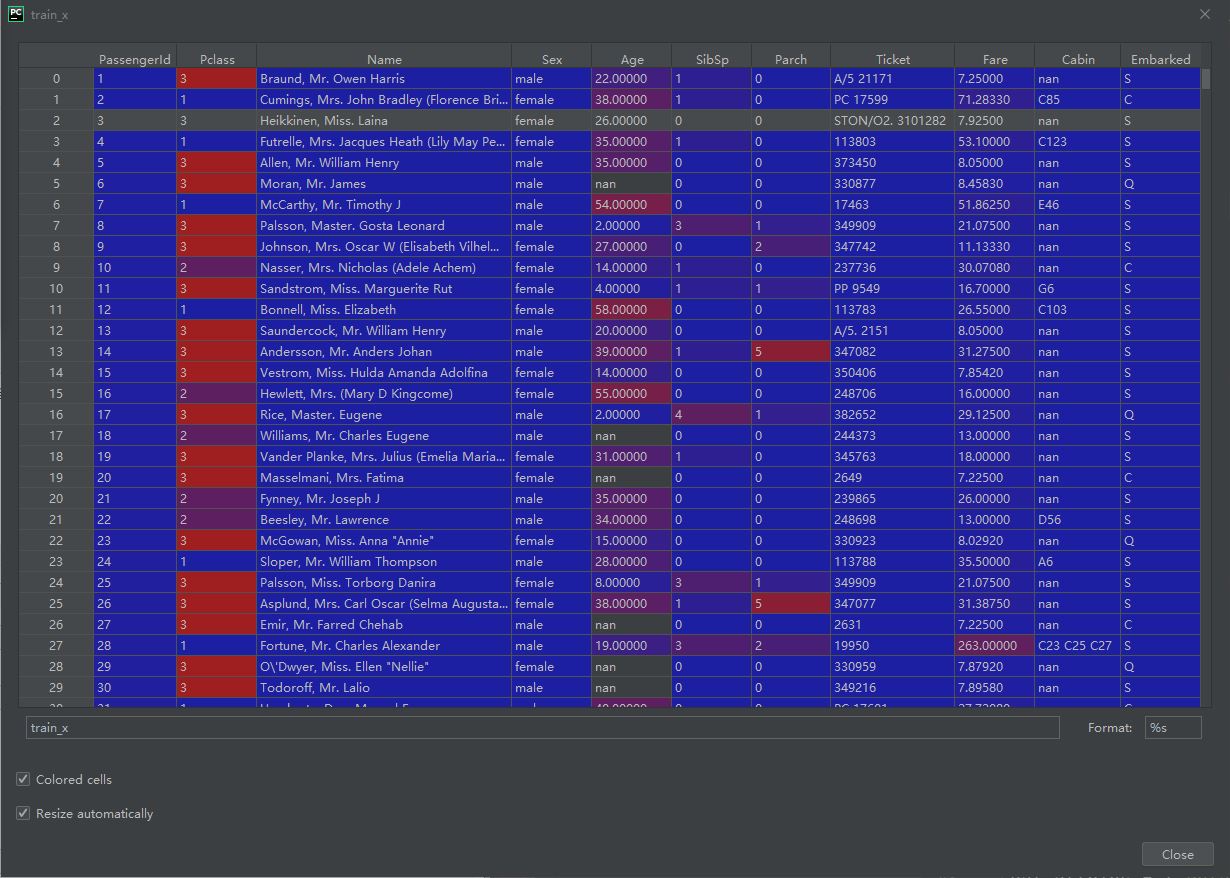
可以初步将数据分为以下几类：

第一类：无意义的。包括PassengerID、Name(其实name可以通过 Mr、Mrs、Miss、Master等进行进一步细分，暂且先不考虑)、Ticket、Cabin(包含太多NAN)

第二类：连续数值类型。包括Age和Fare

第三类：离散数值类型。包括SibSp和Parch

第四类：分类变量。包括Pclass(尽管是数值形式)、Sex和Embarked

后续将使用第二、第三、第四类数据。

 

 4.2 数据清洗

其次，利用sklearn.preprocessing 和 sklearn.impute对数据进行预处理。对于不同类型的数据，其与处理方式不同，如下：

连续数值类型：利用mean对缺失值进行填充。

离散数值类型：利用most frequent对缺失值进行填充。

分类变量：利用most frequent对缺失值进行填充，且需要对变量进行one-hot encoder编码。

看起来比较复杂，幸运的是sklearn提供了Pipeline 和 FeatureUnion 方便了我们对数据的预处理。 

cat_attribs = ['Pclass', 'Sex', 'Embarked']
dis_attribs = ['SibSp', 'Parch']
con_attribs = ['Age', 'Fare'] 

# <editor-fold desc="Pipeline">
# 使用Pipeline 以及 Feature Union对数据进行处理
# Pipeline takes a list of name/estimator pairs defining a sequence of steps
# LabelBinarizer intended for labels only, fit and fit_transform methods include only y
# However, the pipeline (which works on features) sending both X and y
# Multioutput target data is not supported with label binarization
# OneHotEncoder will return a sparse matrix by default, toarray()
cat_pipeline = Pipeline([
    ('selector', DataFrameSelector(cat_attribs)),
    ('imputer', SimpleImputer(strategy='most_frequent')),
    ('encoder', OneHotEncoder()),
])

dis_pipeline = Pipeline([
    ('selector', DataFrameSelector(dis_attribs)),
    ('imputer', SimpleImputer(strategy='most_frequent')),
#    ('encoder', OneHotEncoder())
])

con_pipeline = Pipeline([
    ('selector', DataFrameSelector(con_attribs)),
    ('imputer', SimpleImputer(strategy='mean')),
])

full_pipeline1 = FeatureUnion(
    transformer_list=[
        ('con_pipeline', con_pipeline),
    ]
)

full_pipeline2 = FeatureUnion(
    transformer_list=[
        ('dis_pipeline', dis_pipeline),
        ('cat_pipeline', cat_pipeline),
    ]
)

train_x_cleaned1 = full_pipeline1.fit_transform(train_x)
train_x_cleaned2 = full_pipeline2.fit_transform(train_x)

可以看到了：

1. 为了简化整个Pipeline的流程，Pipeline 中的第一步都是 DataFrameSelector，用于选取train_x中属于这一数据类型的数据。

2. 可以看到对分类变量进行处理时，使用的时OneHotEncoder()，而不是LabelBinarizer也不是我们新定义的MyLabelBinarizer。

LabelBinarizer不能用的原因是，它是针对label进行encoder的，所以它的fit_transform()方法只接收y一个变量；而pipeline整体是作用于feature的，fit_transform()同时传入X和y。

MyLabelBinarizer解决了上述问题，可以同时传入X和y；但我们同时传入多列，相当于是 multioutput，而MyLabelBinarizer基于的LabelBinarizer是不支持 multioutput target data的。

3. 我们将清理后的数据分成了两部分：train_x_cleaned1 和 train_x_cleaned2。这是因为 sklearn 中的Naive Bayes无法同时处理连续值和离散值，我们需要分别对其运算，再进行后处理。

 

 4.3 模型选择

首先，我们对 train_x_cleaned1 和 train_x_cleaned2 分别进行模型运算，对连续数据使用 GaussianNB，对离散数据（包括分类变量）使用MultinomialNB。

clf_gau = GaussianNB()
clf_gau.fit(train_x_cleaned1, train_y)
train_y_predicted1 = pd.Series(clf_gau.predict(train_x_cleaned1))
prob_1 = pd.DataFrame(clf_gau.predict_proba(train_x_cleaned1))
log_prob_1 = pd.DataFrame(clf_gau.predict_log_proba(train_x_cleaned1))

clf_mul = MultinomialNB()
clf_mul.fit(train_x_cleaned2, train_y)
train_y_predicted2 = pd.Series(clf_mul.predict(train_x_cleaned2))
prob_2 = pd.DataFrame(clf_mul.predict_proba(train_x_cleaned2))
log_prob_2 = pd.DataFrame(clf_mul.predict_log_proba(train_x_cleaned2))

接下来，我们希望把这两个结果合并，毕竟合在一起才是完整的数据，有两种方法：

第1种：将得出的prob_1、prob_2（都是连续数值型，且已经是处于[0,1]之间，不用再进行标准化）重新作为输入，再加上一层MultinomialNB，而输出依然是 train_y。、

new_feature = np.hstack((prob_1, prob_2))
clf_gau.fit(new_feature, train_y)
predict = pd.Series(clf_gau.predict(new_feature))

但在这个例子里，这并不是一个好的方法。因为可以看出prob_1中0的probability和1的probability的分布显然不是正态分布。（prob_2一样）

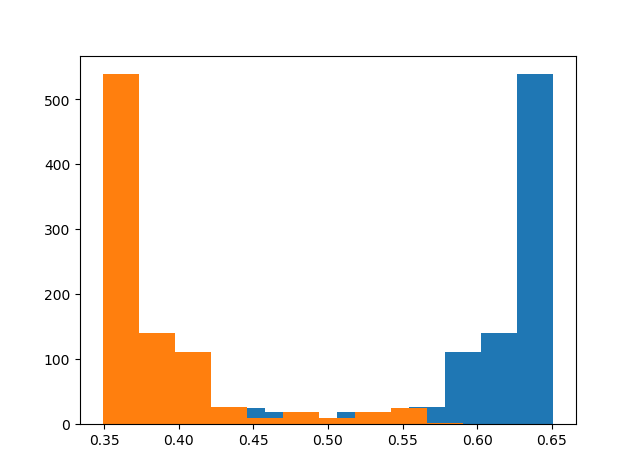
第2种：我们知道朴素贝叶斯是假设条件独立性的，所以可以将两个的prob直接相乘，或者log_prob相加，再进行判断：

temp = log_prob_1 + log_prob_2  #temp = prob_1 * prob_2, 结果是一样的
predict2 = pd.Series(np.zeros(len(prob_1)))
for i in range(0, len(prob_1)):
    if temp.iloc[i, 0] > temp.iloc[i, 1]:
        predict2.iloc[i] = 0
    else:
        predict2.iloc[i] = 1

 

4.4 结果分析

最后，利用sklearn.metrics模块，对以上四个模型进行结果分析，使用accuracy, precision, 和recall。

 

print(accuracy_score(train_y, train_y_predicted1))  # train_y_predict2, predict, predict2
print(precision_score(train_y, train_y_predicted1))
print(recall_score(train_y, train_y_predicted1))

 

	训练集 accuracy	训练集 precision	训练集 recall	预测集 accuracy（需上传kaggle获取结果）
纯Gaussian分布	0.668	0.725	0.216	0.651
纯多项式分布	0.790	0.731	0.716	0.756
联合方法1	0.786	0.758	0.649	0.746
联合方法2	0.749	0.839	0.427	0.742

 

 

 

 

 

 

 

 

 

5. 总结

朴素贝叶斯是一个快速的机器学习方法，虽然往往不是最优的方法，但可以在项目的开始作为一个基准，对后续模型的应用进行评估。

其优点有：

1. 学习、预测效率都很高

2. 没有复杂的模型参数需要调优

3. 概率模型，不存在过度拟合的情况（即便有，也无法改变，只能是数据集本身的特性），因此实战过程中也没有用到 train_test_split

 

其缺点有：

1. 条件独立性假设若不成立，结果将不准确

2. 条件概率的分布的假设若不成立，结果也将不准确