2019 3.27~4.4

还有不几天就省选了，一定要稳住心态，倍加努力

 

 

 

2019 3 27 T1 spy (打表)

题目大意：已知$b_{i}=\sum\limits_{i=0}^{n-1} f((i\;or\;j)\;xor\;i)a_{i}$，现在给出$b$数组，让你还原$a$数组。$n\leq 2^{20}$

打表题..

先考虑暴力怎么写，似乎构造出矩阵F再高消一下就行了，时间复杂度$O(n^{3})$

观察这个矩阵，我们把它分4块，发现它竟然满足这样神奇的性质

左上，左下，右下是同构的，右上则是取反

设$F^{-1}$是$F$的逆矩阵，则$A=F^{-1}B$

观察这个矩阵的性质，发现把最右上角的一个数改成1，得到$G$矩阵

发现左上，右上，右下是同构的，左下则是*-1之后的矩阵，且把这个逆矩阵的每一项乘$2^{n-1}$后，矩阵中只有1和-1

推一下式子

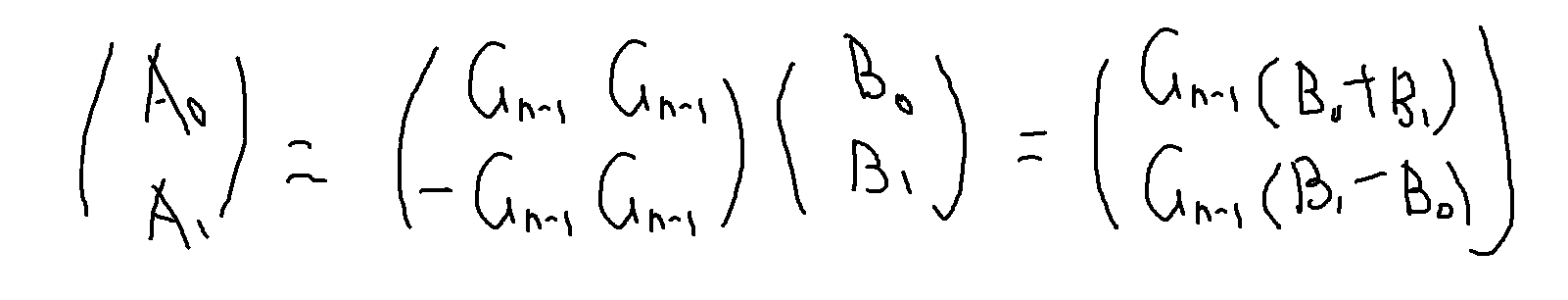
这是什么？蝴蝶操作！我们不断递归下去，最后只剩下一个1*1的矩阵，里面有一个1。

那么我们递归求解一下就行了，别忘了把系数乘回来，再处理一下右上角的贡献

什么？爆long long了，发现蝴蝶操作其实是可逆的，这样就不会用减法减去一个特别大的数了

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N1 1048599
#define ll long long 
#define ull unsigned long long 
#define dd double
using namespace std;

template <typename _T> void read(_T &ret)
{
    ret=0; _T fh=1; char c=getchar();
    while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }
    ret=ret*fh;
}

int n,L;
int a[N1];
ll b[N1],c[N1];

int main()
{
    freopen("spy.in","r",stdin);
    freopen("spy.out","w",stdout);
    scanf("%d",&n);
    int i,j,k,cnt; ll tmp;
    for(i=0;i<n;i++) read(b[i]);
    memcpy(c,b,sizeof(c));
    //for(k=n;k>=2;k>>=1)
    for(k=2;k<=n;k<<=1)
    {
        for(i=0;i<n;i+=k)
        for(j=0;j<(k>>1);j++)
        {
            tmp=c[i+j+(k>>1)];
            c[i+j+(k>>1)]-=c[i+j];
            c[i+j]+=tmp;
        }
    }
    for(L=0;(1<<L)<n;L++);
    for(i=0;i<n;i++) c[i]>>=L-1;
    cnt=(n>>1)-1; c[0]=0;
    for(i=0;i<n-1;i++){ 
        c[0]+=b[i]; while(c[0]>0&&cnt>0) c[0]-=b[n-1], cnt--; }
    c[0]>>=L-1;
    for(i=0;i<n;i++) printf("%lld ",c[i]);
    return 0;
}

 

 

 

2019 3 27 T3 network (容斥+带撤销的并查集)

题目大意：给你一棵$n$个节点的树，有$Q$次修改边权的操作，求每次操作后图中边权$gcd$为1的路径数，$n\leq 10^{5},ei\leq 10^{6},Q\leq 100$

$gcd$为1？考虑利用$\mu$函数容斥的套路，$ans=\sum f(i)\mu(i)$

考虑把询问离线

我们暴力枚举$\mu$不是0的$i$，依次处理修改边权对$f(i)$的影响，然后把$f(i)$的贡献加到这次修改的答案上

对于$n$个节点的树而言，它对能产生的路径数是$n(n-1)/2$

那么现在问题变成，给你一个森林，要我们资瓷断边和连边，同时询问每个连通块内点的个数

并查集？

发现修改次数很少，所以我们先把$i$状态中不会被修改的边路径压缩连在一起，然后把可能会被修改的边按秩合并连在一起，这样就能在能够撤销修改的同时减小常数啦

修改可能是断边，也可能是连边

对于断边而言，假设要被修改的边是e 我们需要把时间戳回溯到连上$e$之前，回溯过程需要把在$e$之后连上的边全都断开，把$e$断开，再重新把e之后断掉的那些边连上，才能保证我们在并查集里只删除了$e$这一条边

对于连边而言，直接连上就行了吧..别忘了修改边对应的时间戳

这个过程时间复杂度是$O(Q^{2}logn)$的

设$10^{6}$范围内$\mu$不为0的数有$K$个，平均因子数是$S$个，那么总时间复杂度是$O(Kn+S(n+Q^{2})logn)$

代码实现极为丧病

#include <vector>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N1 100050
#define O1 105
#define ull unsigned long long 
#define ll long long
using namespace std;
const int maxn=1000000;
#define M1 maxn+10

template <typename _T> void read(_T &ret)
{
    ret=0; _T fh=1; char c=getchar();
    while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }
    ret=ret*fh;
}

struct Edge{ 
int x[N1],y[N1],w[N1],cte;
void ae(int X,int Y,int W)
{ cte++; x[cte]=X; y[cte]=Y; w[cte]=W; }
}e;

int gcd(int x,int y)
{
    if(!y) return x;
    return gcd(y,x%y);
} 

namespace theory{
int fac[N1],num,pfac[N1],d[N1],pnum;
int pr[M1],use[M1],mu[M1],nxt[M1],cnt;
void get_pr()
{
    int i,j; mu[1]=1;
    for(i=2;i<=maxn;i++)
    {
        if(!use[i]){ pr[++cnt]=i; mu[i]=-1; nxt[i]=i; }
        for(j=1;j<=cnt&&i*pr[j]<=maxn;j++)
        {
            use[i*pr[j]]=1; nxt[i*pr[j]]=pr[j];
            if(i%pr[j]){ mu[i*pr[j]]=-mu[i]; }
            else{ mu[i*pr[j]]=0; break; }
        }
    }
}
void dfs_fac(int s,int dep)
{
    if(dep==pnum+1){ fac[++num]=s; return; }
    for(int i=0;i<=d[dep];i++)
    {
        dfs_fac(s,dep+1), s*=pfac[dep];
    }
}
void get_fac(int x)
{
    int i,p; num=pnum=0;
    while(x!=1)
    {
        pfac[++pnum]=nxt[x], d[pnum]=0, p=nxt[x];
        while(x%p==0) d[pnum]++, x/=p;
    }
    dfs_fac(1,1);
}
};

using theory::fac; using theory::num; using theory::mu;

struct Pair{ 
int x,y; 
Pair(int x,int y):x(x),y(y){}
Pair(){}
};
struct node{
int fx,fy,rx,ry,id;
node(int fx,int fy,int rx,int ry,int id):fx(fx),fy(fy),rx(rx),ry(ry),id(id){}
node(){}
};

int n,de;
int opid[N1],opw[N1],mixable[N1],Q,tim[N1]; ll ANS[O1]; bool vis[110];
vector<int>org[M1]; 
vector<Pair>op[M1];
node mix[O1];

int fa[N1],h[N1],sz[N1];
int findfa0(int x){ while(x!=fa[x]) x=fa[x]; return x; }
int findfa1(int x)
{
    int y=x,pre;
    while(y!=fa[y]) y=fa[y];
    while(fa[x]!=y) pre=fa[x], fa[x]=y, x=pre;
    return y;
}
inline ll C(int x){ return 1ll*x*(x-1)/2; }

void cut(node K,ll &sum)
{
    int x=K.fx, y=K.fy, fx=findfa0(x);
    sum-=C(sz[fx]); 
    while(x!=fx) sz[x]-=sz[y], x=fa[x]; sz[x]-=sz[y]; fa[y]=y; 
    sum+=C(sz[fx])+C(sz[y]); 
}

void merge(node &K,ll &sum)
{
    int x=K.rx, y=K.ry;
    x=findfa0(x); y=findfa0(y);
    if(sz[y]>sz[x]) swap(x,y);
    K.fx=x, K.fy=y;
    sum-=C(sz[x])+C(sz[y]); 
    fa[y]=x; sz[x]+=sz[y];
    sum+=C(sz[x]); 
}

void calc(int w)
{
    int i,j,x,y,id,fx,fy,tot=0,t,la=0; ll sum=0,pre; Pair K;
    for(i=0;i<org[w].size();i++)
    {
        x=e.x[org[w][i]]; y=e.y[org[w][i]]; 
        sz[x]=sz[y]=1; fa[x]=x; fa[y]=y;
    }
    for(i=0;i<op[w].size();i++)
    {
        K=op[w][i]; x=e.x[opid[K.y]]; y=e.y[opid[K.y]];
        sz[x]=sz[y]=1; fa[x]=x; fa[y]=y; mixable[opid[K.y]]=1;
    }
    for(i=0;i<org[w].size();i++)
    {
        id=org[w][i]; x=e.x[id]; y=e.y[id]; 
        if(mixable[id]) continue;
        x=findfa1(x); y=findfa1(y);
        sum-=C(sz[x])+C(sz[y]);
        fa[y]=x; sz[x]+=sz[y];
        sum+=C(sz[x]);
    }
    for(i=0;i<org[w].size();i++)
    {
        id=org[w][i]; x=e.x[id]; y=e.y[id]; 
        if(!mixable[id]) continue; 
        mix[++tot]=(node){0,0,x,y,id}; tim[id]=tot;
        merge(mix[tot],sum);
    }
    ANS[0]+=mu[w]*sum; pre=sum;
    /*if(w==2)
        de=1;*/
    memset(vis,0,sizeof(vis));
    for(i=0;i<op[w].size();i++)
    {
        K=op[w][i]; id=opid[K.y];
        for(j=la+1;j<=K.y-1;j++) ANS[j]+=mu[w]*sum; la=K.y;
        if(!K.x){
        
        for(j=tot;j>=tim[id];j--) 
        {
            cut(mix[j],sum); 
        }
        for(j=tim[id];j<tot;j++)
        {
            mix[j]=mix[j+1]; tim[mix[j].id]=j;
            merge(mix[j],sum);
        }
        tot--;
        
        }else{
        
        x=e.x[id]; y=e.y[id];
        mix[++tot]=(node){0,0,x,y,id}; tim[id]=tot;
        merge(mix[tot],sum);
        
        }
        if((i+1==op[w].size()) || (op[w][i].y!=op[w][i+1].y)) ANS[K.y]+=sum*mu[w]; 
    }
    for(j=la+1;j<=Q;j++) ANS[j]+=mu[w]*sum; 
    for(i=0;i<op[w].size();i++)
    {
        K=op[w][i];
        mixable[opid[K.y]]=0;
    }
}

int noww[N1];

int main()
{
    freopen("network.in","r",stdin);
    freopen("network.out","w",stdout);
    int i,j,k,x,y,w,q,tot=0;
    scanf("%d",&n); 
    for(i=1;i<n;i++) read(x), read(y), read(w), e.ae(x,y,w); //e.ae(x,y,z), e.ae(y,x,z);
    theory::get_pr();
    for(i=1;i<n;i++) 
    {
        theory::get_fac(e.w[i]); noww[i]=e.w[i];
        for(j=1;j<=num;j++) if(mu[fac[j]])
            org[fac[j]].push_back(i);
    }
    read(Q);
    for(q=1;q<=Q;q++)
    {
        read(opid[q]); read(opw[q]);
        theory::get_fac(noww[opid[q]]); 
        for(j=1;j<=num;j++) op[fac[j]].push_back(Pair(0,q)); 
        noww[opid[q]]=opw[q];
        theory::get_fac(noww[opid[q]]); 
        for(j=1;j<=num;j++) op[fac[j]].push_back(Pair(1,q)); 
    }
    for(i=1;i<=n;i++) fa[i]=i;
    for(i=1;i<=maxn;i++) if(mu[i])
    {
        calc(i);
    }
    for(q=0;q<=Q;q++) printf("%lld\r\n",ANS[q]);
    return 0;
}

 

 

 

2019 3 29 T2 原样输出 (后缀自动机)

题目大意：给你$n$个字符串，要求你在每个字符串取出一个子串并把它们按顺序连接在一起，形成一个新的串。求不相同的新的串的数量，一些测试点需要按字典序输出这些新串，$\sum len \leq 2^{20}$

后缀自动机好题

众所周知，$SAM$有如下性质：从根节点开始沿着$trs$图走，能走不重不漏地走出这个字符串所有的子串

考虑$n=1$的情况，我们直接对这个串建出$SAM$，并在$trs$图上拓扑即可，输出方案就在$trs$图上贪心$dfs$

如果$n$更大呢？

广义$SAM$并不能很好地解决这个问题..

考虑建出$n$个$SAM$，然后想办法把它们连在一个图里，再用之前的方法求答案，也就是补全trs指针啦

补全$trs$指针的方法和$trie$图类似..

比如当$!trs[x][c]$时，我们要找出$x$所在串$S$后面的串中，第一个出现字符$c$的串$T$，然后把$x$和$c$在$T$的自动机中对应的节点连起来

可以用个队列实现

注意$c$必须是根节点直接连接到的$endpos$节点，不能是辅助节点。因为辅助节点并不是根节点直接到达的，会违背$SAM$的性质

注意输出字符串要用putchar而不是printf，不然会T得很惨

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define N1 1100000
#define M1 N1*3
using namespace std;
const int p=1000000007;

template <typename _T> void read(_T &ret)
{
    ret=0; _T fh=1; char c=getchar(); 
    while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }
    ret=ret*fh;
}

inline int idx(char c)
{
    if(c=='A') return 0;
    if(c=='C') return 1;
    if(c=='G') return 2;
    if(c=='T') return 3;
}
inline char _idx(int x)
{
    if(x==0) return 'A';
    if(x==1) return 'C';
    if(x==2) return 'G';
    if(x==3) return 'T';
}

int n;
char str[N1];
int a[N1],id[N1],Len,to[N1][4],stk[N1],tp; 

namespace SAM{
int trs[M1][4],pre[M1],dep[M1],root[N1],pos[N1],la,tot;
void init(){ la=tot=1; }
int Newroot(){ la=++tot; return tot; }
int insert(int c,int rt)
{
    int p=la,q,np=++tot,nq;
    dep[np]=dep[p]+1; la=np;
    for(;p&&!trs[p][c];p=pre[p]) trs[p][c]=np;
    if(!p){ pre[np]=rt; return np; }
    q=trs[p][c];
    if(dep[q]==dep[p]+1) pre[np]=q;
    else{
        pre[nq=++tot]=pre[q];
        pre[np]=pre[q]=nq;
        dep[nq]=dep[p]+1;
        memcpy(trs[nq],trs[q],sizeof(trs[nq]));
        for(;p&&trs[p][c]==q;p=pre[p]) trs[p][c]=nq;
    }
    return np;
}

int inc[M1],que[M1],hd,tl; ll sum[M1],ANS;
char now[N1];
void print(int dep)
{
    for(int i=1;i<dep;i++) putchar(now[i]); //printf("%c",now[i]);
    ANS++; puts("");
}
void dfs_ans(int x,int dep)
{
    print(dep);
    for(int i=0;i<4;i++)
    {
        if(trs[x][i]) 
        {
            now[dep]=_idx(i);
            dfs_ans(trs[x][i],dep+1);
        }
    }
}
void topo()
{
    int i,c,x;
    hd=1,tl=0; sum[1]=1;
    for(i=1;i<=n;i++) que[++tl]=root[i];
    while(hd<=tl)
    {
        x=que[hd++]; (ANS+=sum[x])%=p;
        for(c=0;c<4;c++) if(trs[x][c])
        {
            (sum[trs[x][c]]+=sum[x])%=p;
            inc[trs[x][c]]--;
            if(!inc[trs[x][c]]) que[++tl]=trs[x][c];
        }
    }
}
void connect()
{
    int i,c,x,j; pos[0]=1;
    for(i=0;i<=Len;i++)
    {
        x=pos[i];
        for(c=0;c<4;c++) if(to[i][c] && !trs[x][c] && id[i]!=id[to[i][c]]) trs[x][c]=pos[to[i][c]];
    }
    for(i=1;i<=tot;i++)
    for(c=0;c<4;c++) if(trs[i][c])
        inc[trs[i][c]]++;
}
void get_to(int c)
{
    int i,j; 
    hd=1,tl=0; que[++tl]=0;
    for(i=1;i<n;i++)
    {
        if(trs[root[i]][c])
            while(hd<=tl) trs[que[hd]][c]=trs[root[i]][c], hd++;
        for(j=root[i];j<=root[i+1];j++)
        {
            if(!trs[j][c]) que[++tl]=j;
        }
    }
    if(trs[root[n]][c])
        while(hd<=tl) trs[que[hd]][c]=trs[root[n]][c], hd++;
}

};



int main()
{
    freopen("copy.in","r",stdin);
    freopen("copy.out","w",stdout);
    int i,j,len,c,K;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
    {
        SAM::root[i]=SAM::Newroot(); 
        scanf("%s",str+1); len=strlen(str+1);
        for(j=1;j<=len;j++)
        { 
            c=idx(str[j]); a[++Len]=c; id[Len]=i;
            SAM::pos[Len]=SAM::insert(c,SAM::root[i]); 
        }
    }
    for(c=0;c<4;c++) SAM::get_to(c);
    scanf("%d",&K);
    SAM::connect();
    if(K==0) SAM::topo();
    else SAM::dfs_ans(1,1);
    printf("%lld\n",SAM::ANS);
    return 0;
}

 

 

 

2019 3 29 T3 不同的缩写 (Trie树+贪心+最大流)

题目大意：给你$n$个串，对于每个串，让你找出一个子序列，最终使得任意两个串找出的子序列都不相同，要求最长的子序列最短，同时输出方案，$n,len\leq 300$

神仙般的模型转化题

用到了一个以前用过的套路然而我考场上还是忘了。对于每个串只需要找出n个子序列就能避免冲突了

最长子序列最短？二分子序列长度上界

找子序列的过程可以用stl的string类+hash+map判重实现

然后建图跑最大流就行了吧

这里又用到了一个小技巧。可以建出$trie$树来表示字符串，判重的同时还得到了代表一个字符串的点的标号

时间O(被卡常)

#include <map>
#include <string>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
#define N1 305 
#define M1 N1*N1*2
#define ull unsigned long long 
using namespace std;
const int seed=131;
const int inf=0x3f3f3f3f;

template <typename _T> void read(_T &ret)
{
    ret=0; _T fh=1; char c=getchar(); 
    while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }
    ret=ret*fh;
}

int idx(char c){ return c-'a'+1; }
char _idx(int x){ return x+'a'-1; }

struct Edge{
int to[M1*3],nxt[M1*3],flow[M1*3],head[M1],cte;
void ae(int u,int v,int f)
{ cte++; to[cte]=v; nxt[cte]=head[u]; head[u]=cte; flow[cte]=f; }
void clr()
{ memset(to,0,(cte+1)*4); memset(nxt,0,(cte+1)*4); memset(flow,0,(cte+1)*4); memset(head,0,sizeof(head)); cte=0; }
}e;

struct Trie{
int ch[M1][27],val[M1],fa[M1],tot;
void clr(){ memset(ch,0,(tot+1)*27*4); memset(val,0,(tot+1)*4); memset(fa,0,(tot+1)*4); tot=0; }
int ins(string &s)
{
    int i,x=0,c;
    for(i=0;i<s.size();i++)
    {
        c=idx(s[i]);
        if(!ch[x][c]) ch[x][c]=++tot, val[tot]=c, fa[tot]=x;
        x=ch[x][c];
    }
    return x;
}
int stk[N1],tp;
void copy(string &s,int x)
{
    s.clear();
    for(tp=0;x;x=fa[x]) stk[++tp]=x;
    while(tp) s+=_idx(val[stk[tp--]]);
}
}tr;

int n,de;

namespace Dinic{

int S,T,N,hd,tl;
int dep[M1],cur[M1],que[M1];

int bfs()
{
    int x,j,v;
    memset(dep,-1,sizeof(dep)); memcpy(cur,e.head,sizeof(cur));
    hd=1,tl=0; que[++tl]=S; dep[S]=0;
    while(hd<=tl)
    {
        x=que[hd++];
        for(j=e.head[x];j;j=e.nxt[j])
        {
            v=e.to[j]; 
            if(dep[v]==-1 && e.flow[j]>0) 
                dep[v]=dep[x]+1, que[++tl]=v; 
        }
    }
    return dep[T]!=-1;
}
int dfs(int x,int limit)
{
    if(x==T||!limit) return limit;
    int j,v,flow,ans=0;
    for(j=cur[x];j;j=e.nxt[j])
    {
        v=e.to[j]; cur[x]=j;
        if((dep[v]==dep[x]+1) && (flow=dfs(v,min(limit,e.flow[j]))))
        {
            e.flow[j]-=flow; limit-=flow;
            e.flow[j^1]+=flow; ans+=flow;
            if(!limit) break;
        }
    }
    return ans;
}
int Main()
{
    int mxflow=0; 
    while(bfs()) mxflow+=dfs(S,inf);
    return mxflow;
}

};

string str[N1],ANS[N1];

map<ull,int>mp;

struct SubStr{
string s[N1]; ull hsh[N1]; int cnt,pos[N1]; 
void clr()
{
    for(int i=0;i<cnt;i++) s[i].clear();
    memset(hsh,0,cnt*8); memset(pos,0,cnt*4);
    cnt=0;
}
void get(int id,int limit)
{
    int i,j,now; ull tmp; char c; mp.clear(); clr();
    for(i=0;i<str[id].size();i++)
    {
        now=cnt; c=str[id][i];
        
        tmp=idx(c);
        if(mp.find(tmp)==mp.end()) 
        {
            mp[tmp]=1;
            s[cnt]=c; hsh[cnt]=tmp; cnt++; 
            if(cnt==n) break;     
        }
        
        for(j=0;j<now;j++)
        {
            if(s[j].size()==limit) continue;
            tmp=hsh[j]*seed+idx(c);
            if(mp.find(tmp)!=mp.end()) continue; mp[tmp]=1;
            s[cnt]=s[j]+c; hsh[cnt]=tmp; cnt++; 
            if(cnt==n) break;
        }
        if(cnt==n) break; 
    }
}
void ins_trie(int id)
{
    int i;
    for(i=0;i<cnt;i++) pos[i]=tr.ins(s[i]);
    for(i=0;i<cnt;i++) e.ae(id,n+pos[i],1), e.ae(n+pos[i],id,0);
}
}F[N1];


int check(int limit)
{
    int i,j,x,v,ans;
    for(i=1;i<=n;i++) F[i].get(i,limit);
    tr.clr(); e.clr(); e.cte=1;
    for(i=1;i<=n;i++) F[i].ins_trie(i);
    for(i=1;i<=n;i++) e.ae(0,i,1), e.ae(i,0,0);
    Dinic::T=n+tr.tot+1;
    for(i=1;i<=tr.tot;i++) e.ae(n+i,Dinic::T,1), e.ae(Dinic::T,n+i,0);
    ans=Dinic::Main();
    if(ans<n) return 0;
    for(x=1;x<=n;x++)
    {
        for(j=e.head[x];j;j=e.nxt[j])
        {
            v=e.to[j]; 
            if(v>n && e.flow[j]==0) 
                tr.copy(ANS[x],v-n);
        }
    }
    return 1;
}

int main()
{
    freopen("diff.in","r",stdin);
    freopen("diff.out","w",stdout);
    int i,j,l,r,mid,ans=-1;
    scanf("%d",&n);
    for(i=1;i<=n;i++) cin >> str[i];
    l=1,r=n; 
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(check(mid)) ans=mid,r=mid-1;
        else l=mid+1;
    }
    if(ans==-1){ puts("-1"); return 0; }
    printf("%d\n",ans);
    for(i=1;i<=n;i++) cout<< ANS[i] << endl;
    return 0;
}

 

 

 

2019 3 30 T1 啊 (博弈+贪心)

题目大意：小绿和小蓝小红和小蓝van游戏，首先给出一棵$n$个点的树，这棵树保证非叶子结点的儿子数量是奇数。他们两人依次在这棵树上还没被填上数字的叶子结点上填数，小红填1，小蓝填-1，直到把叶子结点都填满。可能有一些叶节点一开始就已经被填上了数。非叶子节点的数字=它相邻的儿子中较多的数字。根节点上是数是1则小红赢，反之小蓝赢。问最后谁能赢。如果小红能赢，输出小红第一步可以填数的叶子结点编号。$n\leq 10^{5}$

好一道思维题，输出方案的策略简直神仙。直接把我搞si了

因为每个节点只有奇数个儿子，所以输赢只有3种情况：红必胜，蓝必胜，先手胜

红必胜要满足 红必胜子树数量 > 蓝必胜子树数量

蓝必胜要满足 红必胜子树数量 < 蓝必胜子树数量

先手胜要满足 红必胜子树数量 = 蓝必胜子树数量

DP一下就能判断出谁能赢了

然而本题最duliu的地方在于输出方案

如果根节点是红必胜，那么小红第一步走哪都是赢

如果根节点是先手胜呢？

在一些情况下，小红第一步可以不执行最优策略，但他也能赢！

走先手必胜子树能保证胜利

走红必胜子树会小红导致被翻盘

走蓝必胜子树呢？

当且仅当蓝必胜子树数量-红必胜子树数量=1时，可以走蓝必胜子树

在这种情况下，如果小红往蓝必胜子树内填数，那么小蓝也必须跟着往这棵蓝必胜子树里面填树，小蓝才能保持这个子树是蓝必胜的，否则小蓝会被翻盘

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N1 100010
using namespace std;

template <typename _T> void read(_T &ret)
{
    ret=0; _T fh=1; char c=getchar();
    while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }
    ret=ret*fh;
}

struct Edge{
int to[N1*2],nxt[N1*2],head[N1],cte;
void ae(int u,int v)
{ cte++; to[cte]=v; nxt[cte]=head[u]; head[u]=cte; }
}e;

int n,cnt;
int f[N1],fa[N1],a[N1],ans[N1];

void init()
{
    memset(f,0,sizeof(f)); memset(&e,0,sizeof(e)); 
    memset(ans,0,sizeof(ans)); cnt=0;
}

void dfs(int x)
{
    int j,v,sum=0;
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j]; dfs(v);
        sum+=f[v];
    }
    if(!e.head[x]) f[x]=a[x];
    else{ if(sum>0) f[x]=1; else if(sum<0) f[x]=-1; else f[x]=0; }
}

void dfs_ans1(int x)
{
    int j,v;
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j];
        dfs_ans1(v);
    }
    if(!e.head[x] && !a[x]) ans[++cnt]=x;
}

void dfs_ans0(int x)
{
    int j,v,sum=0;
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j];
        sum+=f[v];
    }
    if(sum!=0 && sum!=1) return;
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j];
        dfs_ans0(v);
    }
    if(!e.head[x] && !a[x]) ans[++cnt]=x;
}

void debug(int x)
{
    while(x) printf("%d:%d\n",x,f[x]), x=fa[x];
    puts("");
}

void deson(int x)
{
    int j,v;
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j];
        printf("%d:%d\n",v,f[v]); 
    }
}

void solve()
{
    int i,j; init();
    scanf("%d",&n); 
    read(fa[1]);
    for(i=2;i<=n;i++) read(fa[i]), e.ae(fa[i],i); // e.ae(fa[i],i);
    for(i=1;i<=n;i++)
    {
        read(a[i]);
        if(a[i]==-1) a[i]=0; else if(a[i]==0) a[i]=-1; else if(a[i]==1) a[i]=1; 
    }
    dfs(1);
    if(f[1]==0||f[1]==-1){
        if(f[1]) dfs_ans1(1);
        else dfs_ans0(1);
        printf("%d ",cnt);
        sort(ans+1,ans+cnt+1);
        for(i=1;i<=cnt;i++) printf("%d ",ans[i]);
        puts("");
    }else puts("-1");
}

int T;
int main()
{
    freopen("ah.in","r",stdin);
    freopen("ah.out","w",stdout);
    scanf("%d",&T);
    for(int t=1;t<=T;t++) solve();
    return 0;
}

 

 

 

2019 3 30 T2 起名字 (树套树)

题目大意：有$n$个硬币，正反两面权值分别为$a_{i},b_{i}$，现在有$m$次操作，每次选择一段区间$[L,R]$，把区间内朝上一面权值不大于$T_{j}$的硬币翻转，求最终所有硬币的权值和

考场上想出分情况讨论了..然而并没有想出如何应用这个策略

因为并不是动态询问硬币的权值和，所以我们暴力枚举每一枚硬币，讨论它最后是那个面朝上就行啦

假设$A<B$，那么操作分为三种，$(0,A),[A,B),[B,inf)$

第一种操作：没卵用

第二种操作：把$A$变成$B$

第三种操作：不管你是$A$还是$B$都翻面

我们只需要关心最后一次第二种操作出现的时间是什么，再在这个时间以后统计第三种操作的次数就好了！！

考虑$L=1,R=n$的情况，好像可以离线+线段树搞搞，虽然思路和正解完全不一样..

加上$L$和$R$的限制之后，需要加一个维度

我们从左到右枚举每一个硬币，插入/删除对当前硬币有影响的操作，可以用排序+堆实现。

这样我们成功消去了一维，还剩下两维，操作时间和操作权值$T$

考虑使用树套树，外层线段树内层平衡树

外层树：操作标号。内层树：权值。

第二种操作就是在线段树上二分查存在性，然后区间查一个数的排名

插入/删除操作就是单点修改，在经过的几个平衡树里把对应节点插入/删除

时间复杂度$O(nlog^{2}n)$

#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N1 100010
#define S1 N1*4
#define ll long long 
using namespace std;

template <typename _T> void read(_T &ret)
{
    ret=0; _T fh=1; char c=getchar();
    while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }
    ret=ret*fh;
}
int de;

struct Splay{
#define M1 N1*20
int ch[M1][2],fa[M1],val[M1],sz[M1],root[S1],tot; 
int idf(int x){ return ch[fa[x]][0]==x?0:1; }
void pushup(int x){ sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+1; }
void rot(int x)
{
    int y=fa[x], ff=fa[y], px=idf(x), py=idf(y);
    fa[ch[x][px^1]]=y; ch[y][px]=ch[x][px^1]; 
    fa[y]=x; ch[x][px^1]=y; fa[x]=ff; ch[ff][py]=x;
    pushup(y); pushup(x);
}
void splay(int x,int to,int id)
{
    if(to==root[id]) root[id]=x;
    int y; to=fa[to];
    while(fa[x]!=to)
    {
        y=fa[x];
        if(fa[y]==to) rot(x);
        else if(idf(x)==idf(y)) rot(y), rot(x);
        else rot(x), rot(x);
    }
}
int ins(int i,int w)
{
    tot++; val[tot]=w; sz[tot]=1; 
    int x=root[i],p; 
    if(!x){ root[i]=tot; return tot; }
    while(1)
    {
        p=(w<val[x]?0:1);
        if(!ch[x][p]){ ch[x][p]=tot; fa[tot]=x; break; }
        x=ch[x][p];
    }
    splay(tot,root[i],i);
    return tot;
}
void des(int x){ ch[x][0]=ch[x][1]=fa[x]=val[x]=sz[x]=0; }
void del(int i,int x)
{
    splay(x,root[i],i);
    if(!ch[x][1]){
        root[i]=ch[x][0]; 
    }else{
        int y=ch[x][1]; root[i]=y;
        while(ch[y][0]) y=ch[y][0];
        ch[y][0]=ch[x][0]; fa[ch[x][0]]=y; //pushup(y);
        splay(y,root[i],i);
    }
    des(x);
}
int qrank(int i,int w)
{
    int x=root[i],ans=0;
    while(x)
    {
        if(w<=val[x]){
            ans+=sz[ch[x][1]]; 
            if(w<=val[x]) ans++;
            if(!ch[x][0]){ splay(x,root[i],i); break; }
            x=ch[x][0];
        }else{
            if(!ch[x][1]){ splay(x,root[i],i); break; }
            x=ch[x][1];
        }
    }
    return ans;
}
#undef M1
}sp;

struct SEG{
int id[N1][18];
void ins(int x,int l,int r,int rt,int D,int w)
{
    id[x][D]=sp.ins(rt,w);
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) ins(x,l,mid,rt<<1,D+1,w);
    else ins(x,mid+1,r,rt<<1|1,D+1,w);
}
void del(int x,int l,int r,int rt,int D)
{
    sp.del(rt,id[x][D]);
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) del(x,l,mid,rt<<1,D+1);
    else del(x,mid+1,r,rt<<1|1,D+1);
}
int qdic(int l,int r,int rt,int ql,int qr)
{
    if(l==r) 
    {
        if(l!=1) return l;
        return sp.qrank(rt,ql)-sp.qrank(rt,qr+1)>0;
    }
    int mid=(l+r)>>1;
    if(sp.qrank(rt<<1|1,ql)-sp.qrank(rt<<1|1,qr+1)>0)
        return qdic(mid+1,r,rt<<1|1,ql,qr);
    return qdic(l,mid,rt<<1,ql,qr);
}
int qsum(int L,int R,int l,int r,int rt,int limit)
{
    if(L<=l&&r<=R) return sp.qrank(rt,limit);
    int mid=(l+r)>>1, ans=0;
    if(L<=mid) ans+=qsum(L,R,l,mid,rt<<1,limit);
    if(R>mid) ans+=qsum(L,R,mid+1,r,rt<<1|1,limit);
    return ans;
}
}seg;

struct OP{ 
int l,r,t,w;
friend bool operator < (const OP &s1,const OP &s2)
{
    if(s1.r!=s2.r) return s1.r>s2.r;
    return s1.t<s2.t;
}
}op[N1];
int cmp(const OP &s1,const OP &s2)
{
    if(s1.l!=s2.l) return s1.l<s2.l;
    return s1.t<s2.t;
}
priority_queue<OP>que;

int n,m;
int a[N1][2];

int main()
{
    freopen("name.in","r",stdin);
    freopen("name.out","w",stdout);
    int i,j,k,l,r,t,w,type,tmp,sum; OP K; ll ans=0;
    scanf("%d",&n);
    for(i=1;i<=n;i++) read(a[i][0]);
    for(i=1;i<=n;i++) read(a[i][1]);
    scanf("%d",&m);
    for(i=1;i<=m;i++) read(op[i].l), read(op[i].r), read(op[i].w), op[i].t=i;
    sort(op+1,op+m+1,cmp);
    for(i=1,k=1;i<=n;i++)
    {
        for(;op[k].l==i;k++) 
        {
            seg.ins(op[k].t,1,m,1,0,op[k].w);
            que.push(op[k]);
        }
        if(a[i][0]==a[i][1]) tmp=a[i][0]; 
        else if(a[i][0]>a[i][1]){
            swap(a[i][0],a[i][1]);
            j=seg.qdic(1,m,1,a[i][0],a[i][1]-1);
            if(j<m) sum=seg.qsum(j+1,m,1,m,1,a[i][1]); else sum=0;
            tmp=(sum&1)?a[i][0]:a[i][1];
        }else{
            j=seg.qdic(1,m,1,a[i][0],a[i][1]-1);
            if(j<m) sum=seg.qsum(j+1,m,1,m,1,a[i][1]); else sum=0;
            if(!j) tmp=(sum&1)?a[i][1]:a[i][0];
            else tmp=(sum&1)?a[i][0]:a[i][1];
        }
        ans+=tmp;
        while(!que.empty())
        {
            K=que.top(); if(K.r!=i) break;
            que.pop(); seg.del(K.t,1,m,1,0);
        }
    }
    printf("%lld\n",ans);
    return 0;
}

 

 

 

2019 4 3 T2 点对游戏 (概率+点分)

题目大意：三个人轮流在$n$个节点树上等概率地选取一个未被占有的节点归为己有。当取完树上所有的节点以后，开始计算的得分。一个人的得分为其占有的节点中，点对的距离为幸运数的点对数量。幸运数数量$m\leq 10,n\leq 5*10^{4}$

考场上并没有发现概率的结论..

如果一个人在树上选择了$x$个节点，那么有$C_{n}^{x}$种选择方案

在这些方案中，他占据某个点对的方案有$C_{n-2}^{x-2}$种

那么他占据这个点对的概率就是$\frac{C_{n-2}^{x-2}}{C_{n}^{x}}$

那其他人呢？打表发现一个人占据某个点对的概率并不会受其他人影响！#喷血

有了上述结论以后，现在我们只需要求出长度为幸运数的链的数量，上点分治即可

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N1 50010
#define dd double
#define ll long long 
using namespace std;
const int inf=0x3f3f3f3f;

template <typename _T> void read(_T &ret)
{
    ret=0; _T fh=1; char c=getchar();
    while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }
    ret=ret*fh;
}

struct Edge{
int to[N1*2],nxt[N1*2],head[N1],cte;
void ae(int u,int v)
{ cte++; to[cte]=v; nxt[cte]=head[u]; head[u]=cte; }
}e;

int n,m,SZ,G;
int usedroot[N1],sz[N1],ms[N1],dep[N1],lucky[12];
int que[N1],tl,bar[N1],stk[N1],tp,use[N1];
ll sum[12];

void gra(int x,int dad)
{
    int j,v; sz[x]=1; ms[x]=0;
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j]; if(v==dad || usedroot[v]) continue;
        gra(v,x); sz[x]+=sz[v]; ms[x]=max(ms[x],sz[v]);
    }
    ms[x]=max(ms[x],SZ-sz[x]);
    if(ms[x]<ms[G]) G=x;
}
void dfs_add(int x,int dad)
{
    int j,v; que[++tl]=x;
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j]; if(v==dad || usedroot[v]) continue;
        dep[v]=dep[x]+1; dfs_add(v,x);
    }
}
void calc(int x)
{
    int j,v,i,k; 
    dep[x]=0; bar[0]=1;
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j]; if(usedroot[v]) continue;
        dep[v]=1; dfs_add(v,x);
        for(i=1;i<=tl;i++)
        {
            for(k=1;k<=m;k++) if(lucky[k]-dep[que[i]]>=0)
                sum[k]+=bar[lucky[k]-dep[que[i]]];
        }
        for(i=1;i<=tl;i++) 
        {
            if(!use[dep[que[i]]]) stk[++tp]=dep[que[i]], use[dep[x]]=1;
            bar[dep[que[i]]]++;
        }
        tl=0;
    }
    while(tp) bar[stk[tp]]=use[stk[tp]]=0, stk[tp]=0, tp--; bar[0]=0;
}
void main_dfs(int x)
{
    int j,v; usedroot[x]=1; calc(x);
    for(j=e.head[x];j;j=e.nxt[j])
    {
        v=e.to[j]; if(usedroot[v]) continue;
        G=0; SZ=sz[v]; gra(v,x); 
        main_dfs(G);
    }
}

int main()
{
    freopen("game.in","r",stdin);
    freopen("game.out","w",stdout);
    int i,j,x,y;
    scanf("%d%d",&n,&m);
    for(i=1;i<=m;i++) read(lucky[i]);
    for(i=1;i<n;i++) read(x), read(y), e.ae(x,y), e.ae(y,x);
    ms[0]=inf; SZ=n; gra(1,0); main_dfs(G); 
    dd ret;
    ret=0; x=n/3+(n%3>=1);
    for(i=1;i<=m;i++) ret+=1.0*x/n*(x-1)/(n-1)*sum[i];
    printf("%.2lf\n",ret);
    ret=0; x=n/3+(n%3>=2);
    for(i=1;i<=m;i++) ret+=1.0*x/n*(x-1)/(n-1)*sum[i];
    printf("%.2lf\n",ret);
    ret=0; x=n/3;
    for(i=1;i<=m;i++) ret+=1.0*x/n*(x-1)/(n-1)*sum[i];
    printf("%.2lf\n",ret);
    return 0;
}

 

 

 

2019 4 3 T3  (状压DP)

题目描述：

一个$ n*m $的棋盘，左上角为$ (1,1)$, 右下角为$ (n,m) $。相邻的 2点之间有连边 （如下图中实线）特殊地，（如下图中实线）特殊地， $(1,i)$ 与$(n,i)$ 也连有一条边（如下图中虚线） 也连有一条边（如下图中虚线） ,i=1..m 。
如下图，就是一个 $n=3,m=4 $的

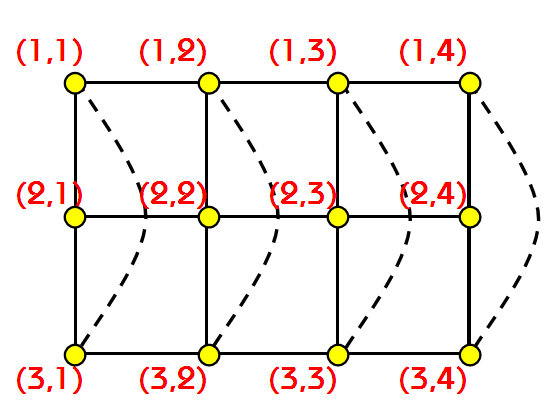
每个点$ (i,j)$ 给定 2个值$ a[i][j],b[j] $。每条边 $e$给定 1个值 $c[e]$ 。

你的任务是给每一个点非负$d$值，最小化$ (S1+S2)$ 。

$S1=\sum_{i=1}^{n}\sum_{j=1}^{m}(d_{ij}\;xor\;a_{ij})b_{ij}$

$S2=\sum_{e}(d_{u}\;xor\;d_{v})c_{e}$

 

会发现都是异或之后再乘，所以位和位之间不会影响，我们对每一位单独处理

把棋盘斜着翻转一下，发现每一行内的点很少，状压DP？

每个点会对它上面和左面以及它自己产生贡献，最后一个格子还和第一个点产生贡献，可以按行进行转移

还可以尝试像插头DP一样按格转移，状态里记录轮廓线，会好写很多

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N1 10500
#define M1 (1<<5)+1
#define dd double
#define ll long long 
using namespace std;
const ll linf=0x3f3f3f3f3f3f3f3f;
const int maxn=(1<<20)-1;

template <typename _T> void read(_T &ret)
{
    ret=0; _T fh=1; char c=getchar();
    while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }
    ret=ret*fh;
}

int n,m;
int a[N1][6],b[N1][6];
int c0[N1][6],c1[N1][6];
ll f[N1][6][M1];

int main()
{
    freopen("chessboard.in","r",stdin);
    freopen("chessboard.out","w",stdout);
    int i,j,s,k,u,l,p,w; ll ans,tmp;
    scanf("%d%d",&n,&m);
    for(i=0;i<n;i++) for(j=1;j<=m;j++) read(a[j][i]);
    for(i=0;i<n;i++) for(j=1;j<=m;j++) read(b[j][i]);
    for(i=0;i<n;i++) for(j=1;j<m;j++) read(c0[j][i]);
    for(i=0;i<n-1;i++) for(j=1;j<=m;j++) read(c1[j][i]);
    for(j=1;j<=m;j++) read(c1[j][n-1]);
    
    for(k=0,ans=0;k<20;k++) {
    
    memset(f,0x3f,sizeof(f));
    f[0][n-1][0]=0;
    for(i=1;i<=m;i++)
    {
        for(j=0,s=0;s<(1<<n);s++)
        {
            if(f[i-1][n-1][s]==linf) continue;
            u=(s>>j)&1; w=(a[i][j]>>k)&1;
            p=0;
            f[i][j][s&(maxn^1)] = min(f[i][j][(s&(maxn^1))], f[i-1][n-1][s]+(p^u)*c0[i-1][j]+(p^w)*b[i][j] );
            p=1;
            f[i][j][s|1] = min(f[i][j][s|1], f[i-1][n-1][s]+(p^u)*c0[i-1][j]+(p^w)*b[i][j] );
        }
        for(j=1;j<n;j++)
        {
            w=(a[i][j]>>k)&1;
            for(s=0;s<(1<<n);s++)
            {
                if(f[i][j-1][s]==linf) continue;
                l=(s>>(j-1))&1; u=(s>>j)&1;
                p=0;
                f[i][j][s&(maxn^(1<<j))] = min(f[i][j][s&(maxn^(1<<j))], f[i][j-1][s]+(p^u)*c0[i-1][j]+(p^l)*c1[i][j-1]+(p^w)*b[i][j]+((j!=n-1)?0:(p^(s&1))*c1[i][j]) );
                p=1;
                f[i][j][s|(1<<j)] = min(f[i][j][s|(1<<j)], f[i][j-1][s]+(p^u)*c0[i-1][j]+(p^l)*c1[i][j-1]+(p^w)*b[i][j]+((j!=n-1)?0:(p^(s&1))*c1[i][j]) );
            }
        }
    }
    for(s=0,tmp=linf;s<(1<<n);s++) tmp=min(tmp,(1ll*f[m][n-1][s]<<k));
    ans+=tmp;
    
    }
    printf("%lld\n",ans);
    return 0;
}