矩阵树定理

矩阵树定理

拉普拉斯矩阵：

定义：

设无向图有 \(n\) 个节点，拉普拉斯矩阵 \(L\) 是一个 \(n*n\) 的矩阵。

1. \(L_{i,i}\) 的值为节点 \(i\) 的度数。
2. \(L_{i,j}\) 的值为节点 \(i\) 和节点 \(j\) 之间相连的边数的相反数。

例如下图：

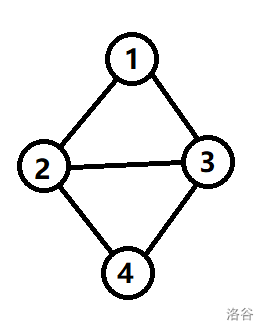
这个图各个节点的度数分别为：\(\{ 2,3,3,2 \}\) ,暂时写成以下矩阵：

\[\quad \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix} \quad \]

然后对于每一条边，我们将 \((i,j)=(j,i)=-1\) ,最终得到的矩阵：

\[\quad \begin{bmatrix} 2 & -1 & -1 & 0 \\ -1 & 3 & -1 & -1 \\ -1 & -1 & 3 & -1 \\ 0 & -1 & -1 & 2 \end{bmatrix} \quad \]

定理：

将拉普拉斯矩阵去掉任意的一行和一列，得到的矩阵求行列式，就是原图的生成树数量。

例如将刚才的矩阵去掉最后一行和一列，得到：

\[\quad \begin{bmatrix} 2 & -1 & -1 \\ -1 & 3 & -1 \\ -1 & -1 & 3 \end{bmatrix} \quad \]

该矩阵的行列式为 \(8\) ，意思是说原图有 \(8\) 个生成树，好像确实是这样，图略。

行列式计算：

行列式有一些性质：

1. 矩阵两行交换，行列式变为相反数
2. 将矩阵的一行 \(+\) (另一行乘一个数)，行列式不变.
3. 三角矩阵的行列式为对角线乘积。

例如之前矩阵，我们将第一行乘 \(\frac{1}{2}\) ,加到第二行，第三行上，得到：

\[\quad \begin{bmatrix} 2 & -1 & -1 \\ -1+2 \times \frac{1}{2} & 3 +(-1)\times \frac{1}{2}& -1 +(-1)\times \frac{1}{2}\\ -1+2 \times \frac{1}{2} & -1 +(-1)\times \frac{1}{2} & 3 + (-1)\times \frac{1}{2}\end{bmatrix} \quad \]

即为：

\[\quad \begin{bmatrix} 2 & -1 & -1 \\ 0 & \frac{5}{2} & -\frac{3}{2} \\ 0 & -\frac{3}{2} & \frac{5}{2} \end{bmatrix} \quad \]

同理，将第二行乘 \(\frac{3}{5}\) ，加到第三行上，得到：

\[\quad \begin{bmatrix} 2 & -1 & -1 \\ 0 & \frac{5}{2} & -\frac{3}{2} \\ 0 & 0 & \frac{8}{5} \end{bmatrix} \quad \]

利用第三条性质，得到矩阵只有右上角的一个三角形内有数，所以我们称其为 三角矩阵

利用类似于高斯消元的想法。

将矩阵上下相减，交换，变换正负号，得到一个三角矩阵。

三角矩阵的行列式就是：有数的对角线乘积，即为：对角线上所有元素的乘积

\[2 \times \frac{5}{2} \times \frac{8}{5} \]

我们发现，这其实就是高斯消元法（不知道高斯消元法也没关系）。但是其中用到了分数，如果模数是质数可以用乘法逆元，否则因为分数在计算机上会有浮点误差，所以我们需要结合没有浮点误差的辗转相除法使用。

辗转相减法：

以比较简单的二阶行列式为例：

\[\quad \begin{bmatrix} 7 & 2 \\ 3 & 5 \end{bmatrix} \quad \]

用第一行不断减去第二行，直到不能继续减，得到：

\[\quad \begin{bmatrix} 1 & -8 \\ 3 & 5 \end{bmatrix} \quad \]

然后交换两行，继续消去(记住要变符号)

\[\quad -\begin{bmatrix} 3 & 5 \\ 1 & -8 \end{bmatrix} \quad \]

\[\quad -\begin{bmatrix} 0 & 29 \\ 1 & -8 \end{bmatrix} \quad \]

\[\quad \begin{bmatrix} 1 & -8 \\ 0 & 29 \end{bmatrix} \quad \]

于是我们就将这个矩阵变成了三角矩阵。

如果更多阶行列式，就要用高斯消元法逐个消去左下的数，使之成为三角矩阵。

推广：

原图有边权：

1. 定义一个节点的度数为 和它相连的边的边权和
2. \(L_{i,j}\) 的值为边 \((i,j)\) 的边权的相反数。

此时求出的值为所有生成树的和，即：

\[\sum\limits_{T为原图的生成树} \qquad \times \qquad \prod\limits_{e为T中的边} edge[e] \]

例题：

P4111 [HEOI2015]小 Z 的房间

题意：

已知无向图，求它的生成树数量

分析：

这题就是一道裸的矩阵树定理的题目，直接套用模板，利用高斯消元解决即可。

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=20,mod=1e9;
char ch[N][N];
int n,m,cnt,ans=1,id[N][N],A[105][105];
void add(int x,int y){
    A[x][y]--;A[y][x]--;
    A[x][x]++;A[y][y]++;
}//拉普拉斯矩阵
signed main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++) cin>>ch[i][j];
    
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(ch[i][j]=='.') id[i][j]=++cnt;
    //将格子进行编号
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            if(ch[i][j]=='.'&&ch[i+1][j]=='.') add(id[i][j],id[i+1][j]);
            if(ch[i][j]=='.'&&ch[i][j+1]=='.') add(id[i][j],id[i][j+1]);
            //只加向下的边和向右的边，防止重复
        }
    cnt--;
    for(int i=1;i<cnt;i++)
        for(int j=i+1;j<=cnt;j++)
            while(A[j][i]){
                int l=A[i][i]/A[j][i];
                for(int k=1;k<=cnt;k++) A[i][k]=(A[i][k]-A[j][k]*l%mod+mod)%mod;
                for(int k=1;k<=cnt;k++) swap(A[i][k],A[j][k]);
                ans*=-1;//每次交换两行，答案取相反数
            }
    for(int i=1;i<=cnt;i++) ans=(ans*A[i][i]%mod+mod)%mod;
    cout<<ans<<endl;    
    system("pause");
    return 0;
}