虚树

虚树

前置要求：

作用：

在树形 \(dp\) 中，一次询问仅仅涉及到整颗数中少量节点时，我们建立一棵只包含关键点的虚树，将非关键点构成的链简化成边或者是剪去，在叙述上进行 \(dp\) 。

虚数包含：

虚树包含所有的询问点和他们的 \(lca\) ,对于 \(k\) 个点的询问，整颗虚树最多有 \(2k-1\) 个节点。

建立要求：

1. 预处理出原树的 \(dfs\) 序以及 \(dp\) 需要用的东西。
2. 在线 \(lca\) 的算法。
3. 将询问点按 \(dfs\) 序排序。

建立过程：

初始将第一个询问点加入栈中。

将接下来所有的询问点加入，询问点为 \(now\)，\(lc\) 为该点和栈顶点最近公共祖先 \(lc=lca(stack[top],now)\)。

分情况讨论 \(lc\) 与栈中第二个元素 \(stack[top-1]\) 的关系。

1:\(lc=stack[top]\), \(now\) 在 \(stack[top]\) 的子树中。

此时整个树成一条链，我们只需要把 \(now\) 入栈，把他加到最右链的末端。

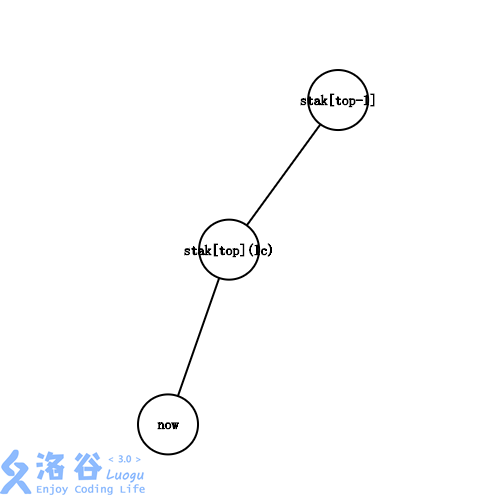
2：\(lc\) 在 \(stack[top]和stack[top-1]\) 之间。

显然，此时最右链的末端从 \(stack[top-1]->stack[top]\) 变成了 \(stack[top-1]->lc->stack[top]\) 。

我们需要做的，首先是把边 \(lc->stack[top]\) 加入虚树。

然后，把 \(stack[top]\) 出栈，把 \(lc\) 和 \(now\) 入栈。

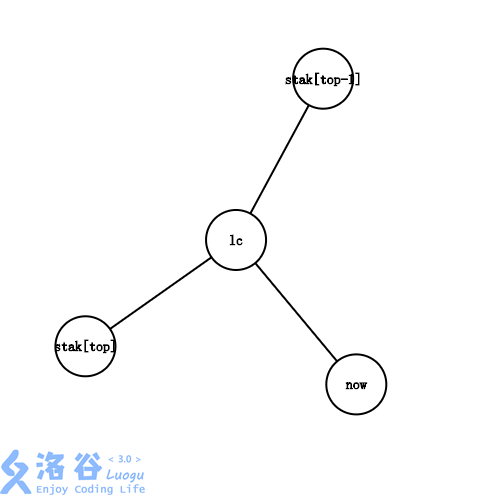
3:\(lc=stack[top-1]\)

和第二种情况差不多，就是 \(lc\) 不用入栈了。

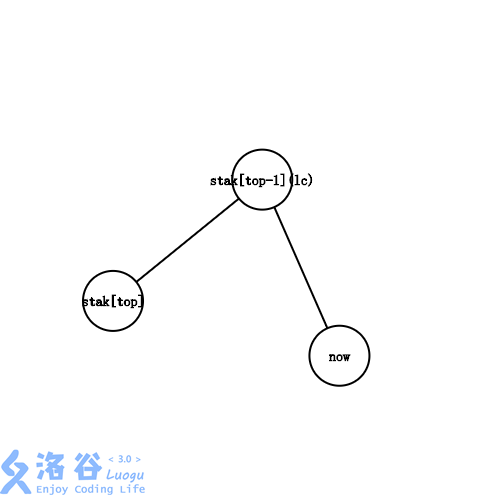
4:\(lc\) 不在 \(stack[top-1],stack[top-2]....\) 的子树中。

此时 \(dep[lc]<dep[stack[top-1]]\)。

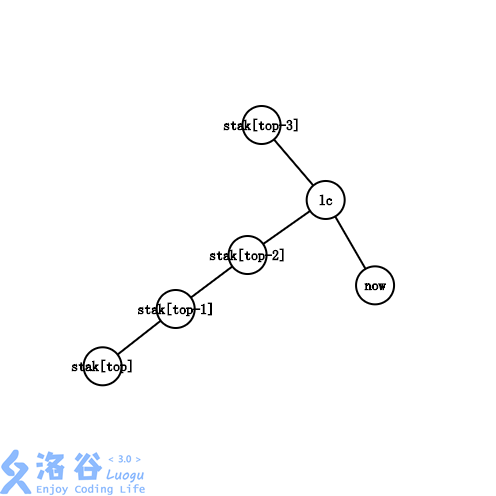
以图中为例，最右链从

\(stak[top-3]->stak[top-2]->stak[top-1]->stak[top]\)

变成了 \(stak[top-3]->lc->now\)。

我们需要循环依次将最右链的末端剪下，将被剪下的边加入虚树，直到不再是情况四。

就上图而言，循环会持续两轮，将 \(stak[top],stak[top−1]\) 依次出栈。

并且把边 \(stak[top−1]−stak[top],stak[top−2]−stak[top−1]\) 加入虚树中。随后通过情况二完成构建。

结尾：

当最后一个询问点加入之后，再将最右链加入虚树，就完成了构建。

例题：

P2495 [SDOI2011]消耗战

代码：

#include <bits/stdc++.h>
#define INL inline
#define REG register
#define DB double
#define LDB long double
#define ULL unsigned long long
#define LL long long

#define RPT(i,x,y) for (REG int i=x;i<y;i++)
#define DRPT(i,x,y) for (REG int i=x;i>y;i--)
#define MST(a,b) memset(a,b,sizeof(a))

#define MAXN 500500
#define MAXM 10000
#define MOD 998244353
#define INF 0x3f3f3f3f
#define LLINF 0x3f3f3f3f3f3f3f3f 
#define EPS 1e-5

#define _ 0
using namespace std;

int dfn[MAXN];
int dep[MAXN];
int fa[MAXN][25];
LL minv[MAXN];
int m[MAXN];
int lst[MAXN];
bool query[MAXN];
int n,q;
int num;
int top;
int dfscnt=1;

int stak[MAXN];

struct EDGE
{
	int to,next;
	LL val;
}edge[MAXN<<1],edge1[MAXN<<1]; 

int head[MAXN];//初始图存储 
int cnt=1;
INL void add(int x,int y,LL v)
{
	edge[cnt].next=head[x];
	edge[cnt].to=y;
	edge[cnt].val=v;
	head[x]=cnt++;
}

int head1[MAXN];//虚树存储 
int cnt1=1;
INL void add1(int x,int y)
{
	edge1[cnt1].next=head1[x];
	edge1[cnt1].to=y;
	head1[x]=cnt1++;
}

void dfs(int pos)
{
	int k;
	for (k=0;fa[pos][k];k++)
		fa[pos][k+1]=fa[fa[pos][k]][k];
	m[pos]=k;
	dfn[pos]=dfscnt++;
	for (int i=head[pos];i;i=edge[i].next)
	{
		REG int to=edge[i].to;
		if (!dfn[to])
		{
			dep[to]=dep[pos]+1;
			minv[to]=min(minv[pos],edge[i].val);
			fa[to][0]=pos;
			dfs(to);
		}
	}
}

LL dfs1(int pos) //dp
{
	LL sum=0;
	LL tem;
	for (int i=head1[pos];i;i=edge1[i].next)
	{
		int to=edge1[i].to;
		sum+=dfs1(to);
	}
	if (query[pos])
		tem=minv[pos];
	else
		tem=min(minv[pos],sum);
	query[pos]=false; //清空虚树 
	head1[pos]=0;
	return tem;
}

int lca(int x,int y) //倍增LCA 
{
	if (dep[x]<dep[y])
		swap(x,y);
	DRPT(i,m[x],-1)
		if (dep[fa[x][i]]>=dep[y])
			x=fa[x][i];
	if (x==y)
		return x;
	DRPT(i,m[x],-1)
		if (fa[x][i]!=fa[y][i])
		{
			x=fa[x][i];
			y=fa[y][i];
		}
	return fa[x][0];
} 

bool cmp(int x1,int x2)
{
	return dfn[x1]<dfn[x2];
}

int main()
{
	minv[1]=LLINF;
	cin>>n;
	int x,y;
	LL v;
	RPT(i,0,n-1)
	{
		scanf("%d%d%lld",&x,&y,&v);
		add(x,y,v);
		add(y,x,v);
	}
	dfs(1);
	cin>>q;
	while (q--)
	{
		cin>>num;
		RPT(i,1,num+1)
		{
			scanf("%d",&lst[i]);
			query[lst[i]]=true;
		}
		sort(lst+1,lst+num+1,cmp);
		stak[top=1]=lst[1];
		RPT(i,2,num+1)
		{
			int now=lst[i];
			int lc=lca(now,stak[top]);
			while (1)
				if (dep[lc]>=dep[stak[top-1]])
				{
					if (lc!=stak[top]) //不满足该条件为情况一 
					{
						add1(lc,stak[top]);
						if (lc!=stak[top-1]) //情况二 
							stak[top]=lc;
						else //情况三 
							top--;
					}
					break;
				}
				else //情况四
				{
					add1(stak[top-1],stak[top]);  
					top--;
				}
			stak[++top]=now; //最后统一把now压进栈中 
		}
		while (--top)
			add1(stak[top],stak[top+1]); //将最右链放进虚树 
		cout<<dfs1(stak[1])<<endl;
		cnt1=1;
	}
	return ~~(0^_^0);
}