ACM散题习题库4【持续更新】

 

401. 不降子数组游戏【二分】

直接二分就行。因为getAns函数写错了，wa了几发。（当nxt[l]>r的时候，这个时候就是递增子数组，就是数组长度的组合数）

 

402. 子串（数据加强版）【组合数】

一开始想到了从两边遍历，然后把1单独拎出来，后面没想到切入口。

然后看到严gg的文章，同一段0的隔板数量应该是一样的，特判一下0作为数组开头的情况，然后计算就行了。

查看代码

void solve() {
  initAC();
  cin >> n >> str + 1;
  int l = 0, r = n + 1;
  ans = 1;
  while (l < r) {  // 不能加等号
    int pl = l + 1, pr = r - 1;
    while (pl < r && str[pl] != '1') pl++;
    while (pr > l && str[pr] != '1') pr--;
    if (pr < pl) {
      int len = (pl - pr);
	  if (l == 0) len -= 2;  
      ans = (ans * qpow(2, len) % mod);
      break;
    } else {
      int mn = min(pl - l, r - pr), mx = max(pl - l, r - pr);
      ll sum = 0;
	  if (l == 0) mn--, mx--;
      for (int i = 0; i <= mn; i++)
        sum = (sum + C(mn, i) * C(mx, i) % mod) % mod;
      ans = (ans * sum) % mod;
      l = pl, r = pr;
    }
  }
  cout << ans << endl;
}

 

403. F - String Cards (atcoder.jp)【排序 + DP】题解

感觉这一题字符串连接起来字典序最小很神奇。

（1）第一步，排序。根本就没想这种排序方法，我一开始还以为直接按字典序排序。

可能也是一个常见的结论了吧。字符串连接得到的大字符串的字典序根据拓扑图来构建是最优的。【这个结论需要记住捏】

（2）第二步，01背包。因为构建好拓扑图之后，并不能直接按照拓扑序直接选前k个，比如：(2, 1, ["b", "ba"])这组数据。或者说，拓扑序是不唯一的，直接选拓扑序的前k个得到的不一定是最小答案。

（3）‘{’的ASCII刚好是123，‘z’的ASCII是122，刚好比字母大。

查看代码

 vector<string> ss;
string dp[51];
int n, k;

bool cmp(string a, string b) { return a + b < b + a; }

void solve() {
  cin >> n >> k;
  ss.assign(n, string());
  for (int i = 0; i < n; i++) {
    cin >> ss[i];
  }
  sort(all(ss), cmp);
  dp[0] = "";
  for (int i = 1; i <= n; i++) dp[i] = "{";
  for (int i = n - 1; i >= 0; i--) {
    for (int j = min(k, n - i); j; j--) dp[j] = min(dp[j], ss[i] + dp[j - 1]);
  }
  cout << dp[k] << endl;
}

 

404. 放置多米诺骨牌 【二分图 + 黑白染色】【题解】

经典的不重叠的多米诺骨牌，很自然的想到了二分图上面去（而且直方图是一个二分图）。

然后黑白染色跑最大匹配就行了，因为是直方图，黑白染色直接for一遍就行了（假设第一个点是白，那么依次向上染；然后下一列的第一个点就是黑）

 

405. 变量【贪心思维 / wqs二分暴力DP】

（1）方法1：把数组排序，然后看成n-1个数，然后选其中n-k小的数加起来就是答案。

（2）方法2：wqs二分优化DP。然后在cnt的地方，不知道什么原因被卡了一下（以后还是cnt越小越好了）。

考虑复杂度为nk的DP，然后用wqs二分优化掉后面的k。

需要注意的就是：wqs二分的时候，数值相等的时候应该选谁（在这道题里面，数值相等就选择c[i]-c[i-1]而不是添加一个新的块）。

因为我二分里面写的是cnt小于等于k，就更新答案ans，所以相同权值的情况下，cnt越小越好（就是wqs二分的那个常见问题）。

查看代码

 int n, k, c[maxn];

PLL get(ll m) {
  ll ans = m, cnt = 1;
  for (int i = 2; i <= n; i++) {
    if (m < c[i] - c[i - 1]) {
      cnt++, ans += m;
    } else {
      ans += c[i] - c[i - 1];
    }
  }
  return {ans, cnt};
}

void solve() {
  cin >> n >> k;
  for (int i = 1; i <= n; i++) cin >> c[i];
  sort(c + 1, c + 1 + n);
  ll L = 0, R = 2e10, mid;
  while (L < R) {
    mid = (L + R) >> 1;
    if (get(mid).se <= k) R = mid;
    else L = mid + 1;
  }
  cout << (get(R).fi - k * R) << endl;
}

 

405. 谁才是最终赢家？【思维 + 博弈 + 打表】【题解】

不太理解严格鸽写的题解，难道两个人一定会走完所有格子吗？

然后就是用打表代码打出了规律出来，直接交了一发。。。。。

打表代码

 struct Node {
  vector<vector<int>> vis;
  int value, x, y;
  Node(int N) { x = y = value = 0, vis.assign(N, vector<int>(N, 0)); }
  void calcValue() {
    value = (1ll * x * 1919810 + y) % mod;
    int pw = 1;
    for (int i = 0; i < vis.size(); i++) {
      for (int j = 0; j < vis[i].size(); j++) {
        value = (value + pw) % mod;
        pw = (pw * 2) % mod;
      }
    }
  }
  bool operator<(const Node &rhs) const { return value < rhs.value; }
  bool operator==(const Node &rhs) const {
    if (x != rhs.x || y != rhs.y) return false;
    if (vis.size() != rhs.vis.size()) return false;
    for (int i = 0; i < vis.size(); i++) {
      if (vis[i].size() != rhs.vis[i].size()) return false;
      for (int j = 0; j < vis[i].size(); j++) {
        if (vis[i][j] != rhs.vis[i][j]) return false;
      }
    }
    return true;
  }
};

map<pair<int, Node>, int> SG;
int n = 5, x, y;

int dfs(int tp, Node x) {
  if (SG.count(make_pair(tp, x))) return SG[make_pair(tp, x)];
  // up 
  if (x.x > 0 && !x.vis[x.x - 1][x.y]) {
    int nx = x.x - 1;
    Node tx = x;
    tx.x = nx;
    tx.vis[tx.x][tx.y] = 1;
    tx.calcValue();
    if (!dfs(!tp, tx)) return true;
  }
  // down
  if (x.x < n - 1 && !x.vis[x.x + 1][x.y]) {
    int nx = x.x + 1;
    Node tx = x;
    tx.x = nx;
    tx.vis[tx.x][tx.y] = 1;
    tx.calcValue();
    if (!dfs(!tp, tx)) return true;
  }
  // left
  if (x.y > 0 && !x.vis[x.x][x.y - 1]) {
    int ny = x.y - 1;
    Node tx = x;
    tx.y = ny;
    tx.vis[tx.x][tx.y] = 1;
    tx.calcValue();
    if (!dfs(!tp, tx)) return true;
  }
  //right 
  if (x.y < n - 1 && !x.vis[x.x][x.y + 1]) {
    int ny = x.y + 1;
    Node tx = x;
    tx.y = ny;
    tx.vis[tx.x][tx.y] = 1;
    tx.calcValue();
    if (!dfs(!tp, tx)) return true;
  }
  return false;
}

void solve() {
  cin >> n >> x >> y;
  if (n & 1) {
    cout << ((x + y) & 1 ? "Alice" : "Bob") << endl;
  } else {
    cout << "Alice" << endl;
  }
  
  SG.clear();
  Node cur(n);
  // cin >> cur.x >> cur.y;
  cur.x = x, cur.y = y;
  cur.x--, cur.y--;
  cur.vis[cur.x][cur.y] = 1;
  cur.calcValue();
  cout << (dfs(0, cur) ? "Alice" : "Bob") << endl;
}

 

406. 序列中ab的个数 【概率DP + 逆向求解】【题解】

不会做这道题。一开始乱分析，以为第i次操作会增加(pa)/(pa+pb)*(i-1)个ab子序列，然后输麻了。

看了题解才发现，原来要用DP来求解，而且需要逆向求解。

首先定义状态\(f[i][j]\)为当前抽的卡中有i个a，已经有j个ab子序列，那么最后的期望答案是多少。

然后思考一下，得到状态转移公式：\(f[i][j] = \frac{pa}{pa+pb}*f[i+1][j] + \frac{pb}{pa+pb}*f[i][i+j]\)

upd：我又想错了，我以为递推式是:\(f[i][j] = \frac{pa}{pa+pb}*f[i+1][j] + \frac{pb}{pa+pb}*(f[i][i+j]+j)\) 。。。。不懂期望。是不是因为期望线性性啊。平时我们遇到的步数期望，一般都是\(F(x)=(p_1*F(y)+p_2*F(z)+...)+1\)的，这道题并不是算步数期望，而是算最后结果的期望，既然\(F[i][j]\)已经算好了答案，那么通过概率分类讨论结果进行转移，是不是也是可以理解？

然后无穷无尽地推下去 （

当然，我们找到一个递归终止点：当i+j>=k&&j<k时，直接赋值：\(f[i][j] = i+j+pa/pb\)

具体分析以及原因，严格鸽题解里面有。

然后记忆化搜索就做完了。。。。。。好讨厌概率DP啊，每一次都不会。

 

407. 选元素（数据加强版）【暴力DP / wqs二分优化DP】

呃，说是数据加强，结果也就2500，暴力都可以过。

然后使用wqs二分+单调队列DP可以优化到\(O(n*logn)\)，好耶。

一开始没想到wqs二分能做（也不太懂为什么能做------呃，直接上套路不如）

定义的DP状态为：dp[i]表示最后一个点选在i的最优答案，然后直接把dp[i]存到单调队列里面。

细节：注意单调队列，最后还要加一个while循环删掉n-k之前的才是对的。

查看代码

 int n, x, k, a[maxn];

struct Node {
  ll val, cnt;
  int id;
  bool operator>(const Node& rhs) const {
    if (val != rhs.val) return val > rhs.val;
    return cnt < rhs.cnt;
  }
};

PLL get(ll M) {
  deque<Node> q;
  q.push_back(Node{0, 0, 0});
  for (int i = 1; i <= n; i++) {
    while (q.size() && q.front().id < i - k) q.pop_front();
    ll val = q.front().val + a[i] - M, cnt = q.front().cnt + 1;
    Node cur = {val, cnt, i};
    while (q.size() && cur > q.back()) q.pop_back();
    q.push_back(cur);
  }
  while (q.size() && q.front().id <= n - k) q.pop_front();
  return {q.front().val, q.front().cnt};
}

void solve() {
  cin >> n >> k >> x;
  for (int i = 1; i <= n; i++) cin >> a[i];
  if (x * k + (k - 1) < n) {
    cout << -1 << endl;
    return;
  }
  ll L = 0, R = 2e14, mid;
  while (L < R) {
    mid = (L + R) >> 1;
    if (get(mid).se < x)
      R = mid;
    else
      L = mid + 1;
  }
  cout << (get(R).fi + x * R) << endl;
}

 

408. 序列中位数【数学 、 找规律】

（1）根据gcd(a,n)=gcd(n-a,n)=1可以知道，[1,n/2],[n/2+1,n]之间与n互质的数是镜像的。那么可以进一步得到，互质的中位数一定是小于等于n/2且与n互质的最大的那个数，然后暴力去找竟然十分快。

（2）直接打表找规律，可以找到一个4个数字为一组的规律。

 

409. 矩阵游戏【构造 + 思维 + 图论 + 二分图生成树计数】【题解】

一开始以为是在n*m的矩阵中放置n+m-1个点，然后每行每列至少一个点。这样我就用容斥直接做，然后wa了。。。

看了题解之后，发现需要建图，然后完全二分图K{n,m}的生成树数量是:\(n^{m-1}*m^{n-1}\)。这个结论可以记一下。

同样的矩阵游戏中的生成树，还有这么一道题：P5089 [eJOI2018] 元素周期表 看生成树缺了多少条边即可。

查看代码

 int qpow(int x, int y) {
  int r = 1;
  for (; y > 0; y >>= 1, x = ((ll)x * x) % mod)
    if (y & 1) r = ((ll)r * x) % mod;
  return r;
}

int n, m;

void solve() {
  cin >> n >> m;
  cout << (1ll * qpow(n, m - 1) * qpow(m, n - 1)) % mod << endl;
}

 

410. P4552 [Poetize6] IncDec Sequence【经典差分题 / 三分+二分+并查集 】

tm的，一开始根本没想到差分，暴力三分+并查集卡过去了。。。。捏嘛，菜死了。

然后发现这是一道经典的差分思维题。

（1）问题1：最少多少次可以使得数组一致？区间加减1，可以转变成差分数组上面的左端点加减1，右端点+1处减加1。最少的情况下，应该是正负相互抵消，最后剩下的无法抵消，就只能自身加减1了。所以答案就是max(abs(差分数组负数之和),差分数组正数之和)

（2）问题2：最后数组会有多少种可能？差分数组从n个数变成n-1个差值，同时第一位的数字不变。那么数组最后的数字，就跟第一位数字有关。

第一个数字什么时候变？当我们正负抵消完成之后，假设正数之和还有x，那么我们可以进行两种操作：①d[0]+x,d[i]-x；②d[i]-x,d[n+1]+x

这两种操作，说明了第一个数有x+1种可能！（因为只有操作1才会改变第一个数，操作1可以执行0~x次）

所以问题二的答案就是 1 + llabs(差分数组数值之和，不包括第一个数)。

然后再说说三分，三分一个X，计算让所有数变成X的步数，显然是一个单峰函数，直接做就行。

 

411. P4006 小 Y 和二叉树 【贪心 + 模拟】

题意：给定一棵二叉树，要你求出它中序遍历最小的形态。

（1）先找出度数小于3的最小的节点start。

（2）从start开始遍历，依次向上填father和向下填right_son。充填的依据是dp的值 。

（3）上面说到dp的值，其实就是以start为根的树中，dp[x]表示x的子树中最小中序遍历的第一个数（这个理解了之后，这道题就很好做了）。

（4）然后再多写几个if-else就可以通过了。

 

412. P4438 [HNOI/AHOI2018]道路  【树形DP + 思维】

这道题数据范围是解题关键，因为树的深度不超过40，所以可以加上40*40表示有多少个公路、铁路没修。

然后这个DP状态设计也是比较妙的 -> 主要是逆向思维。

定义：\(f[x][i][j]\) 表示从1到x有i条公路没修、有j条铁路没修的最小贡献。

转移 就是：\(f[x][i][j] = min(f[lson][i+1][j]+f[rson][i][j], f[lson][i][j] + f[rson][i][j+1])\)

然后答案就是：f[1][0][0]。

感觉挺妙的。

查看代码

 ll f[maxn][41][41];
int n, son[maxn][2];
int a[maxn], b[maxn], c[maxn];

ll dfs(int x, int i, int j, int dep) {
  if (i > dep || j > dep) return inf_ll;
  if (x < 0) 
    return 1ll * c[-x] * (a[-x] + i) * (b[-x] + j);
  if (f[x][i][j]) return f[x][i][j];
  return f[x][i][j] = min(
    dfs(son[x][0], i + 1, j, dep + 1) + dfs(son[x][1], i, j, dep + 1),
    dfs(son[x][0], i, j, dep + 1) + dfs(son[x][1], i, j + 1, dep + 1)
  );
}

void solve() {
  cin >> n;
  for (int i = 1; i < n; i++) 
    cin >> son[i][0] >> son[i][1];
  for (int i = 1; i <= n; i++) 
    cin >> a[i] >> b[i] >> c[i];
  cout << dfs(1, 0, 0, 0) << endl;
}

 

413. P4928 [MtOI2018]衣服？身外之物！【N进制状态 + DP】

这道题不算难，但是问的问题老是让我想复杂了。。。（但是数据范围n<=4，y<=6，说明存在某种围绕n、y的暴力做法）

然后就是定义状态f[7][7][7][7][2000]表示第0件衣服还有多少天洗完，第1件还有多少天.....，2000表示2000天。

然后就是暴力记忆化转移就行了。

 

414. P4959 [COCI2017-2018#6] Cover【斜率优化DP + 最简单情况】

题意：在保证矩形中心在（0,0）的情况下，使用多个矩形来覆盖n个点，同时输出所有矩形面积之和。

首先把所有点坐标取个绝对值，放在第一象限（这是合理的），然后按x从小到大排好序。再用y坐标做一遍单调栈（这个是为了斜率优化DP中的坐标单调）。

然后套用最简单的斜率优化DP的模板就行了。（之前没记笔记，有点忘了，结果磨了一个小时。。。我是sb）

查看代码

 struct Node {
  int x, y;
  bool operator<(const Node& rhs) const {
    return x < rhs.x || (x == rhs.x && y < rhs.y);
  }
} a[maxn];

int n, que[maxn], L, R;
ll dp[maxn];

double getSlope(int i, int j) {
  return - (1.0 * dp[i] - dp[j]) / (1.0 * a[i + 1].y - a[j + 1].y);
}

void solve() {
  cin >> n;
  for (int i = 1, x, y; i <= n; i++) {
    cin >> x >> y;
    x = abs(x), y = abs(y);
    a[i] = {x, y};
  }
  sort(a + 1, a + 1 + n);

  // 提前维护好单调性x单调递增，y单调递减
  int tn = n;
  n = 0;
  for (int i = 1; i <= tn; i++) {
    while (n && a[i].y >= a[n].y) n--;
    a[++n] = a[i];
  }

  // 斜率优化DP：y是(-a[i+1].y)作为横坐标，dp[i]作为纵坐标
  // 转移方程：dp[i] = dp[j] + (y[j+1]*x[i])
  // 假设k>j，k转移比j优的时候，有斜率不等式：
  // -(dp[k]-dp[j])/(y[k+1]-y[j]) <= x[i]
  que[L = R = 1] = 0;
  a[0] = {0, inf_int};
  for (int i = 1; i <= n; i++) {
    while (L < R && getSlope(que[L], que[L + 1]) <= a[i].x) L++;
    int j = que[L];
    dp[i] = dp[j] + (a[j + 1].y * a[i].x);
    // 这里如果getSlope(R-1,R)>getSlope(R-1,i)
    // 而根据最优选择：-(dp[i]-dp[j])/(y[i+1]-y[j+1])<x
    // 说明斜率应该越小越好，所以pop掉斜率大的一个
    // 从形状上来理解，就是在维护凸包
    while (L < R && getSlope(que[R - 1], que[R]) >= getSlope(que[R - 1], i)) R--;
    que[++R] = i;
  }
  cout << dp[n] * 4 << endl;
}

 

415. 与 【思维 + 完全背包求解方程非负整数解的数量】

题意：

把题目转换成：求\(x_0+2*x_1+...+2^t*x_t=n\)解的数量，其中t大概是logn。

因为t十分小，可以使用完全背包求解 - 我用的是记忆化搜索，常数大很多。

当然，类似于这种求方程解的数量的，还可以使用容斥（比如后面这一题）。（不知道多项式那些高科技能不能解决这个问题）

 

416. 逆序对数列【经典逆序对问题】

先理解\(O(n^3)\)的做法，自然就会优化成：\(O(n^2)\)了。

定义：\(dp[i][j]\)表示\([1,i]\)这\(i\)个数形成的所有数列中，逆序对数量为\(j\)有多少种可能。

转移方程：\(dp[i][j]=\sum^{min(i-1, j)}_{k=0} dp[i-1][j-k]\)

理解：对于第\(i\)位，它的逆序对数\(a\)贡献的范围是：\([0,i-1]\)。假设第\(i\)位贡献了\(i-1\)，那么可以把数组\([1:i-1]\)的\(i-1\)个数加\(1\)，第\(i\)放一个1，使得数列合法；假设第\(i\)位贡献了\(i-2\)，那么可以把数组\([1:i-1]\)中除了\(1\)以外的\(i-2\)个数加\(1\)，第\(i\)位放一个\(2\)，使得数列合法；其它以此类推。

然后再学一个：\(O(k*\sqrt(k))\)的做法，虽然没什么用，但是这个做法来求解方程组解的数量貌似很有用的。

 

 

学会这一题，就可以看看这道题了：P6035 Ryoku 的逆序对【思维 + 贪心】

416这题给我们的最大的启发就是，每一个位置的逆序对数范围可以是：\([0, i-1]\)，那么倒过来就是:\([0,n-i]\)。

所以每个\(-1\)对答案的贡献是：\(ans*=n-i+1\)。 （因为总有办法达到n-i+1个数中的某一个，这是可以构造出来的）

所以第一问我们就求出来了。

第二问就是用平衡树贪心就行了，pbds库真香。

 

 

417. C. Prefix Product Sequence【思维 + 构造】

首先判断什么时候有解。

经过几次手糊，发现1一定要在第一位（否则会出现相邻两位相同），n一定要在最后一位（因为最后一定是0）。

然后至少要满足前缀积中不会出现0，也就是1~n-1的乘积不等于0，那么也就只有质数/4/1才满足这些条件了。（n=1和n=4是可以自己找出答案的）

因为后面保证了n是质数，而且n是质数我们一定是可以构造出答案的，所以这就是充要条件。

怎么构造呢？a[1]=1,a[i]=i*inv(i-1)，a[n]=n，这就是答案。。。。。

呜呜呜，主要是没想到可以直接乘逆元抵消掉上一位的影响，呜呜呜。

 

418. P4562 [JXOI2018]游戏【从箱子抽取所有黑球的期望次数-经典模型 + 计数】

读清楚题：相当于一个箱子有k个黑球，n-k个白球，然后问所有情况中抽取所有黑球所需要的次数的总和。

（1）使用埃式筛筛取所有区间伪质数（即不是区间内其他数倍数的数）。 - 这个复杂度是：\(O(n*loglogn)\)的，因为质数数量大致是：\(O(n/lnn)\)左右的

当然你可以用欧拉筛求出每个数的最小因子，如果x/p(x)<l的话，说明x不是[l,r]区间内其它数的倍数。

（2）然后抽黑球这个经典模型的期望次数是：\(k*(n+1)/(k+1)\) - 可以根据dls教的期望线性性来证明，也可以使用组合数。

（3）最后，期望*情况种数 = 每种情况的权重之和。 - 这个公式之前竟然没怎么注意？还是说只有在这题才生效?

具体就是上面几步。

一开始我还都错题了。。。。

读成：老板会检查到多少个办公室的员工没有工作（一开始所有办公室都在摸鱼）。

然后就是求出每个数在[l,r]区间内约数的数量k（不包括自己），然后一个数对答案贡献1，当且仅当它在所有的约数之前出现。所以就是\((n-k-1!)*C(n,k+1)\)

呃，然后求区间内一个数约数数量的话，只会用埃式筛nlogn来暴力求。。。。

 

 

419. P4678 [FJWC2018]全排列【逆序对数列的数量】 - 参考416那道题

题意：求n!个排列P1和n!个排列P2中，有多少对四元组（P1，P2，l，r）满足P1[l:r]相似于P2[l:r]。两个排列相似，当且仅当离散化后它们是一样的。

答案就是：\(\sum^n_{i=1}((C(n,i)*(n-i)!)^2*(n-i+1)*cnt[i][E])

前半部分是从两个排列中选取i个数，并放在n-i+1任意一个缝隙中。

cnt[i][E]代表长度为i，且逆序对数量小于等于E的排列数之和 - 根据P416那一题，然后做一个前缀和即可。

注意取模1e9+7。

 

420. 矩阵行列乘法求和  P4521 [COCI2017-2018#4] Automobil【乘法交换律 / 暴力维护交点】

（1）做法1：因为k<=1000，每一次涉及一行/一列，然后每次都for一遍出现过的行/列，维护一下交点。这种做法可以在线维护答案，即每次询问之后都可以回答。复杂度：\(O(k^2)\)

（2）做法2：详细看洛谷题解。因为乘法具有交换律，所以先把所有行操作乘上去，然后把n*m的矩阵压缩成m列的向量，然后再暴力维护向量。这样做可以实现复杂度：\(O(n+m+k)\)

做法2貌似很神奇，代码在这里：

查看代码

 struct Query {
  char op;
  int x, y;
} a[maxn];

int n, m, k, F[maxn], val[maxn];

void solve() {
  cin >> n >> m >> k;
  for (int i = 1; i <= k; i++) 
    cin >> a[i].op >> a[i].x >> a[i].y;
  for (int i = 1; i <= n; i++) val[i] = 1;
  for (int i = 1; i <= k; i++)  // 先乘上每一行的操作 
    if (a[i].op == 'R') 
      val[a[i].x] = (1ll * val[a[i].x] * a[i].y) % mod;
  int sumMul = 0;
  for (int i = 1; i <= n; i++)
    sumMul = (sumMul + val[i]) %mod;
  F[1] = 0;  // 先计算第一列
  for (int i = 1; i <= n; i++) 
    F[1] = (F[1] + (1ll * (i - 1) * m % mod + 1) * val[i] % mod) % mod;
  for (int i = 2; i <= m; i++)  // 根据等差数列来求每一列的和
    F[i] = (F[i - 1] + sumMul) % mod; 
  for (int i = 1; i <= k; i++)  // 再乘上每一列的操作
    if (a[i].op == 'S') 
      F[a[i].x] = (1ll * F[a[i].x] * a[i].y) % mod;
  ll ans = 0;
  for (int i = 1; i <= m; i++)  // 最后求和
    ans = (ans + F[i]) % mod;
  cout << ans << endl;
}

 

421. P4376 [USACO18OPEN]Milking Order G【二分 + 拓扑排序】

题意：给你m条边，让你判断最多能取多少条边（从1开始连续的取，所以存在单调性 ），使得整个图仍然是有向无环图。

麻了，一开始一直在想是否能把并查集魔改一下，用于判断有向图是否成环。然后就G了。。。。。

其实直接二分就行了，单调性很显然的。。。。。。。然后每次二分完都拓扑排序一遍就行了。。。

 

 

422. P3664 [USACO17OPEN] Modern Art P【二维差分求一个点被多少个矩形覆盖】

题意：给出一个矩阵G，g[i][j]代表这个位置的颜色，1~n*n中每个颜色都会只涂一遍，求有多少个颜色一定覆盖了其它颜色。

大概就是求出每个颜色的最左边、最下边、最上边、最右边的边界，然后二维差分一下-差分完求二维前缀和。

这样就可以得到每个位置被多少个矩形覆盖，如果一个位置被多个矩形覆盖，那么最顶上的矩形一定覆盖了其它矩形。

又因为矩形都是连通块，覆盖关系会形成一个有向无环图的。 - 这个和题目没有关系。。。。

 

 

423. P4422 [COCI2017-2018#1] Deda 【cdq分治 / 线段树上二分】

题意：每次更新插入一个年龄为A，下车的车站号为X的小孩；每次询问查询所有年龄大于等于B，在区间[1,Y]之间下车的所有小孩中的最小年龄。

（1）思路1：遇到这种有两个指标的，同时自带时间轴的题目，一眼看出是三维数点可以做。

细节：遇到查询的点不要插入到set里面！！！！我没注意，wa了一个小时。。。。。尼玛

（2）思路2：线段树上二分。

因为这道题他要查询1个年龄就行了，不需要计数什么的其它的操作。所以根据年龄段[1,n]建一棵线段树，然后对于每个年龄维护他下车的最小车站ID。然后查询的时候，在线段树[B,n]区间内二分就行了。

二分一个k：满足[B,k]区间内的最小值小于等于Y。然后可以直接在线段树上二分优化掉一个logn！

这种类似三维偏序问题，但是实际上只是涉及到一个点查询，可以用线段树上二分来做！

 

424. P4264 [USACO18FEB]Teleportation S 【离散分段函数 + 绝对值分类讨论 + map枚举转折点 + 差分求每一个离散点的斜率...】

f(y)的形状大体是这样的：

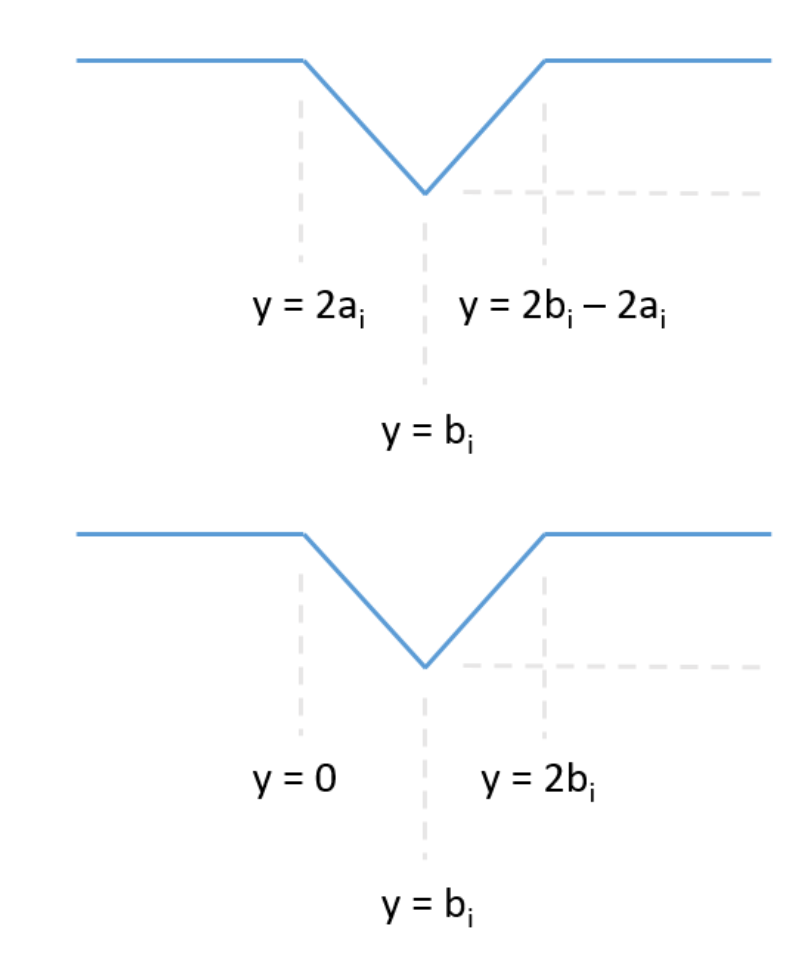
然后根据我们分类讨论得出的临界点，差分地记录每个点对斜率造成的变化（这里不知道是不是应该用斜率来形容比较恰当）也可以看出多个函数求和，整个函数的斜率等于所有函数的斜率之和。。。。。这个结论就在后面用到了。具体看代码。

查看代码

 map<int, int> delta;
int n;

void solve() {
  cin >> n;
  ll tot = 0;
  for (int i = 1, a, b; i <= n; i++) {
    cin >> a >> b;
    tot += abs(a - b);
    if (abs(a - b) <= abs(a)) continue;
    delta[b] += 2;
    // 这里一定仔细按照分类讨论写，一开始我还写成了 abs(a)>=abs(b)
    // 但是两者显然不一样，比如a=-2，b=7
    if ((a < b && a < 0) || (a >= b && a >= 0)) {
      delta[0]--, delta[2 * b]--;
    } else {
      delta[2 * b - 2 * a]--, delta[2 * a]--;
    }
  }
  ll ans = tot, k = 0, lasy = -inf_int;
  for (auto [y, d] : delta) {
    tot += (y - lasy) * k;
    lasy = y, k += d;
    ans = min(ans, tot);
  }
  cout << ans << endl;
}

 

 

425.  数学课 【概率论 + 经典思维 + 数列求和(平方和、立方和)】【题解】

一开始暴力去解，发现公式过于复杂。。。。

看了题解，才发现，可以利用a和b的来源是相互独立的，得出P(a>b)=P(a<b)，所以P(a<b)=(1-P(a==b))/2。

有了上面的结论，就可以去推P(a==b)了。

但是因为取a分为先取v1，再从[1,v1]之间抽数字两步，所以概率的计算并不简单。（而且抽到a=1还可以通过多种方式得到，所以还要计算有多少种方式求出a等于某个数。。。。是不是想得太复杂了。。。）

\([1]\)可以从{1,3,6...}中抽取，\([2,3]\)可以从{3,6....}中抽取，[4,6]可以从{6,.......}中抽取。 - 通过观察可以得知，区间\([\frac{i*(i-1)}{2}+1,\frac{i*(i+1)}{2}]\)可以有n+1-i个来源。

又因为数列 \(a_i = (i+1)*i/2\)，抽到\(a_i\)的概率我们已知。

在抽到某个i的前提下，抽取一个a=x的概率是：

再根据我们观察出每个数的来源有多少个，可以算出抽到任何一个数的概率：

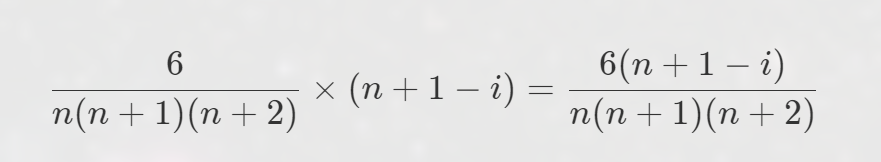
所以a=b的概率就是遍历所有数，\(p=\sum_{x<a_n} p(a=x)*p(b=x)\)

又因为一个区间内i个数的概率是一样的，我们写成：\(p=\sum^n_{i=1}i*p(a=x)*p(b=x)\)这样就可以把概率压在一起求和，复杂度O(n)。

但是还是不够，我们继续化简，最后变成了O(1)的计算式子。 - 化简过程中直接暴力拆开 \(((n+1)-i)^2\) 这一项，然后用平方和、立方和求和，最后刚好可以抵消分母的一部分，很巧妙。

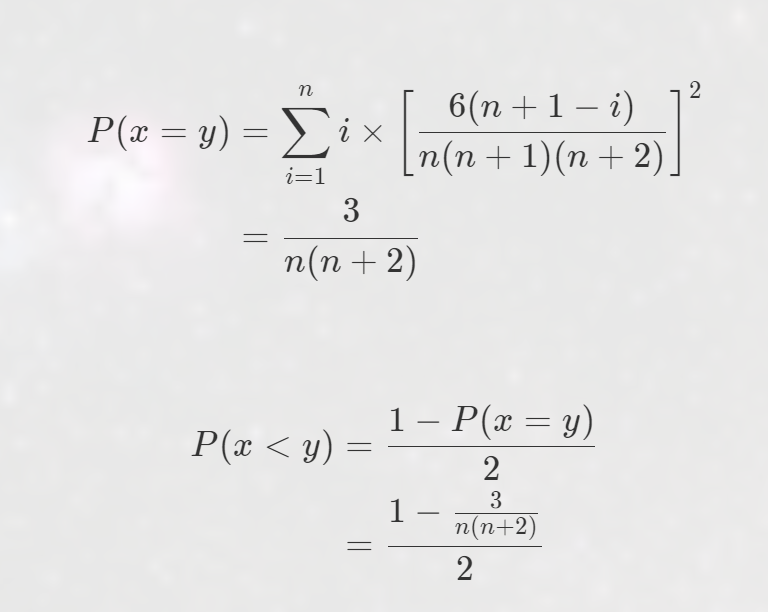
细节：只需要n和n+2不是998244353的倍数，该式子是有解的。

 

 

426. P5426 [USACO19OPEN]Balancing Inversions G【01数组 + 逆序对  + 思维题】【题解】

（1）把逆序对计算转换成数学模型 - 计算公式。

（2）考虑枚举左侧1的数量x，右侧1的数量可以同时计算出来。

（3）移动相邻两个数 -> 说明只能通过中间分界线交换1，所以贪心地选取最靠近边界的1。

（4）经过第3步，左右侧1的数量已经固定，那么公式的右侧已经固定，只剩下\(\sum a-\sum b\)。因为交换1、0会导致1的位置和减少或者增加1，是连续变化的。所以直接拿右侧的数减去当前1的位置和即可。

最后记得开longlong。

查看代码

 int n, one, a[maxn];
vector<int> L0, L1, R0, R1;

void solve() {
  cin >> n;
  for (int i = 1; i <= 2 * n; i++) cin >> a[i], one += a[i];
  ll TsumL = 0, TsumR = 0, ans = inf_ll;
  for (int i = 1; i <= n; i++)
    if (a[i]) L1.emp(i), TsumL += i;
    else L0.emp(i);
  for (int i = n + 1; i <= 2 * n; i++)
    if (a[i]) R1.emp(i), TsumR += i - n;
    else R0.emp(i);
  ll tmpL = TsumL, tmpR = TsumR, sum = 0;
  int pl = L1.size(), pr = 0;
  for (int x = L1.size(), y; x >= 0; x--) {
    y = one - x;
    if (x <= n && y <= n) {
      int K = (one - 1 - 2 * n) * (y - x) / 2;
      ans = min(ans, abs(K - (tmpL - tmpR)) + sum);
    }
    if (pl > 0 && pr < R0.size()) {
      sum += R0[pr] - L1[--pl];
      tmpL -= L1[pl];
      tmpR += R0[pr++] - n;
    } else break;
  }
  tmpL = TsumL, tmpR = TsumR, sum = 0;
  pl = L0.size(), pr = 0;
  for (int y, x = L1.size(); x <= one; x++) {
    y = one - x;
    if (x <= n && y <= n) {
      int K = (one - 1 - 2 * n) * (y - x) / 2; 
      ans = min(ans, abs(K - (tmpL - tmpR)) + sum);
    }
    if (pl > 0 && pr < R1.size()) {
      sum += R1[pr] - L0[--pl];
      tmpL += L0[pl];
      tmpR -= R1[pr++] - n;
    } else break;
  }
  cout << ans << endl;
}

 

427. P5428 [USACO19OPEN]Cow Steeplechase II S【平面几何 + set + 扫描线 + 线段相交】

题意：让你删除1条线段，使得其它所有线段都不相交。（数据保证有解）

扫描线+线段相交的思想：不理解。

这道题用set做感觉有点怪怪的。。。。感觉是假做法，不会证明，也不太直观理解，就这样吧。

 

 

428. P5454 [THUPC2018]城市地铁规划【生成树 + 思维 + 背包 + prufer序列构造一棵树】

--  简单了解prufer的一些性质 ：blog --

题意：让你构造一棵树，其中第i号节点的度数为\(d_i\)，那么这棵树的权值为：\(\sum F(d_i)\)。其中F是一个多项式函数，系数给定，次数k<=10。

题目给的模数只是为了不溢出，最大值是取模意义下的。

做法：

（1）为了保证是一棵生成树，一开始假设每个点的度数为1。那么剩下了n-2的度数来分配 - 这个思想很重要，因为度数分配完毕，就可以根据prufer序列构造这么一棵树，节点的编号是不重要的。

（2）转换为一个完全背包问题，n个物品，第i个物品体积为i，背包总体积为n-2。那么要做的就是确定n-2的体积的最大价值 - 价值就是多项式函数的值之和。

（3）通过DP求出最优解，同时记录转移路径，最后确定每个度数出现了多少次，然后根据prufer构造一下就行了。 - 完全背包可以使用\(O(n)\)的空间记录转移！这一点可以带来空间上的优化，很棒。

查看代码

 int n, k, a[20];
ll W[maxn], DP[maxn], pre[maxn];

void solve() {
  cin >> n >> k;
  for (int i = 0; i <= k; i++) cin >> a[i];

  // 计算W数组
  for (int i = 0; i <= n; i++)
    for (int j = k; j >= 0; j--) W[i] = (W[i] * i % mod + a[j]) % mod;
  // 特判
  if (n == 1) {
    cout << 0 << " " << W[0] << endl;
    return;
  }
  if (n == 2) {
    cout << 1 << " " << W[1] * 2 << endl;
    return;
  }
  // 做 DP + pre 记录 - 完全背包记录转移空间可以做到On
  DP[0] = n * W[1];
  for (int i = 1; i <= n - 2; i++) {
    for (int j = i; j <= n - 2; j++) {
      if (DP[j] < DP[j - i] + W[i + 1] - W[1]) {
        DP[j] = DP[j - i] + W[i + 1] - W[1];
        pre[j] = j - i;
      }
    }
  }
  // 通过prufer构造输出
  int totID = 0, curID = n;
  cout << n - 1 << " " << DP[n - 2] << endl;
  vector<int> ID;
  for (int i = n - 2; i; i = pre[i]) {
    int du = i - pre[i];
    while (du--) ID.emp(curID);
    curID--;
  }
  reverse(all(ID));
  for (int i = 0; i < ID.size(); i++) 
    cout << ++totID << " " << ID[i] << endl;
  cout << ++totID << " " << n << endl;
}

 

 

429. P5521 [yLOI2019] 梅深不见冬 【思维 + 贪心 + 树上问题】【题解】

因为题目要求按照dfs的方式遍历整棵树，所以我们对于一个节点来说，必须遍历完它自己再继续去遍历它的兄弟。也就是说，子树的答案是固定的情况下，只有遍历的顺序会影响父节点的答案

同时，我们把父节点的答案计算公式写出来，ans[x]=max(ans[x], preSum + ans[v] + rest); 其中rest=max(0, W[x] - (ans[v] - W[v])); preSum是之前遍历的兄弟的W权值之和。

可以看出，ans[v]越小，ans[x]同样会越小，至少不会因为ans[v]的变小而变大。 - 所以可以直接根据儿子的答案ans[v]来推导ans[x]。

但是遍历儿子的顺序怎么确定呢？ - 可以使用贪心+数学归纳法的思想。

假设1~i-2的儿子的遍历顺序是最优的，我们现在确定i-1、i这两个位置应该放(a、b)还是放(b、a)。

假设tmp[i]是ans[x]遍历到第i个儿子时的答案。

（1）假设a在b之前，得到答案的推导式子：

  \(tmp[i] = max(tmp[i-2], (W_1+...+W_{i-2})+ans[a]+rest_a, (W_1+...+W_{i-1})+ans[b]+rest_b\) - 可以发现 \(rest_a、rest_b\)在此刻都是常数。

（2）假设b在a之前，得到答案的推导式子：

  \(tmp[i] = max(tmp[i-2], (W_1+...+W_{i-2})+ans[b]+rest_b, (W_1+...+W_{i-1})+ans[a]+rest_a\)

（3）如果tmp[i]=tmp[i-2]，a和b的顺序任意一个即可；所以我们考虑tmp[i]>tmp[i-2]的情况：

  假设a在b之前更优，则有：\(max(ans[a] + rest_a, W[a] + ans[b] + rest_b) < max(ans[b] + rest_b, W[b] + ans[a] + rest_a)\)

  可以进一步推出：\(W[a] + ans[b] + rest_b < W[b] + ans[a] + rest_a\)

所以对儿子根据 \((ans[b] + rest[b] - W[b])\) 从大到小排序即可，如果a比b优，那么a的排序值比b要大 - 满足偏序关系。

查看代码

 int n, W[maxn], ans[maxn];
vector<vector<int>> son;

void dfs(int x) {
  for (int& v : son[x]) 
    dfs(v);
  sort(all(son[x]), [&](int i, int j) { 
    return ans[i] - W[i] + max(0, W[x] - (ans[i] - W[i])) 
      > ans[j] - W[j] + max(0, W[x] - (ans[j] - W[j])); 
  });
  int preSum = 0, rest;
  ans[x] = W[x];
  for (int& v : son[x]) {
    rest = max(0, W[x] - (ans[v] - W[v]));
    ans[x] = max({ans[x], preSum + ans[v] + rest});
    preSum += W[v];
  }
}

void solve() {
  cin >> n;
  son.assign(n + 1, {});
  for (int i = 2, fa; i <= n; i++) 
    cin >> fa, son[fa].emp(i);
  for (int i = 1; i <= n; i++) 
    cin >> W[i];
  dfs(1);
  for (int i = 1; i <= n; i++) 
    cout << ans[i] << " ";
  cout << endl;
}

 

430. P5677 [GZOI2017]配对统计【数据结构 + 计数思维 + 离线 + 二维数点】

这道题读错题了，题目的意思一开始求出所有(x,y)匹配对，每次查询(l,r)，看看有多少对满足：\((l \le x) && (x \le r) && (l \le y) && (y \le r)\ )...

而我读成了，每次查询[l,r]区间的子数组，然后求出该子数组有多少配对对。

如果不是读错题，就是朴素二维数点。

否则目前只想到莫队+set的\(O(n*\sqrt(n)*logn)\)的做法。

因为每个数都一定有至少一个配对对，所以问题就是求出[l,r]子数组有多少个位置的配对对数量为2。

每次移动指针，都要check一下cur、prev(cur)、next(cur)是否会影响答案即可。 - 假设cur是当前需修改的数的iterator。

不知道有什么做法可以优化掉set的logn。

 

431. P5679 [GZOI2017]等差子序列【bitset暴力 / 分块优化卷积】

① 题意：给定一个数组，判断是否存在(i,j,k)使得 \(a_j-a_i=a_k-a_j\)

枚举一个j是否存在i<j和k>j使得a[j]-a[i]=a[k]-a[j]。可以使用 bitset加速一下。 - 直接暴力即可，不需要使用差分数组。

但是如果数据的ai范围更大的时候，只能用分块优化卷积。- 什么是分块优化卷积（洛谷第一篇题解提了一下，但是没有代码）

然后搜了一下，搜到了这篇东西：多项式牛顿迭代的分块优化 - 博客 - rogeryoungh的博客 (uoj.ac)

细节：bitset清0的时候，需要判断是否还有这个数字（所以需要multiset来维护多个数的存在性）

查看代码

 bitset<40010> L, R;
multiset<int> LS;
int n, a[maxn], O = 20005;

void solve() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> a[i];
  if (n <= 2) {
    cout << "NO" << endl;
    return;
  }
  LS.clear(), L.reset(), R.reset();
  for (int i = 1; i <= n; i++) L[O - a[i]] = 1, LS.insert(O - a[i]);
  for (int i = n; i > 1; i--) {
    // 删除一个数
    LS.erase(LS.find(O - a[i]));
    if (!LS.count(O - a[i])) L[O - a[i]] = 0;
    // 判断
    if (((L << a[i]) & (R >> a[i])).any()) {
      cout << "YES" << endl;
      return;
    }
    // 加上一个数
    R[O + a[i]] = 1;
  }
  cout << "NO" << endl;
}

② 还有一道一模一样的（P2757 [国家集训队]等差子序列）终于找到了回文串的解法。 【提交记录】

我们先令b[a[i]]=i, 然后遍历b[i]。对于一个b[i], 我们想要得到一个k，使得 b[i-k], b[i+k], 在b[i]的两侧。

假设当前枚举到b[i]，我们定义如果b[j]< b[i]，那么c[j]=1；否则c[j]=0。

那么我们就是判断b[i]为重心的字符串c是不是回文串即可。如果是回文串，那么意味着没有答案；如果不是回文串，那么一定存在一个解。

使用线段树维护hash就可以解决这道巧妙的题目。

【启发】由于这道题是01串，base可以选择为2？然后使用单hash卡过去（x 但是双hash也是可以base为2的。 

③ 还有一道差不多的：CF452F Permutation 也是用这种做法来做。

 

 

432. P5835 [USACO19DEC]Meetings S【经典蚂蚁碰撞题目】

这道题不同于蓝书蚂蚁，他要求[1,T]时刻之间发生了多少次碰撞。

先给出结论1：

（1）因为蚂蚁碰撞可以视为直接穿过(在这一题还有交换重量的条件)，因为建模是直接穿过的，所以单从蚂蚁到达终点来看，分别是\(t_1...t_i..t_n\)这些时刻。【即每个时刻一定有一只蚂蚁到达终点】

（2）蚂蚁的重量weight的相对位置不会改变，因为穿过之后重量也会交换。所以在每个时刻到达终点的一定是序列的头或者尾。

（3）所以得到结论：如果\(d_i=-1\)，第\(t_i\)个时刻，序列左端点的蚂蚁到达终点x=0；否则是序列右端点的蚂蚁到达终点x=L。

现在通过这个结论我们可以快速计算T的大小。

再给出结论2：

重量的问题只是限制了T，如今我们计算出T，重量数组就没有用了。

对于每只蚂蚁，只有和他反向相对着走的蚂蚁才会碰撞（即一定是往右走的蚂蚁A和往左走的蚂蚁B碰撞，且A在B的左侧）。

为了避免重复计数，只考虑对每只往左走的蚂蚁来二分。

当\(|X_A-X_B|<=2*T\)的时候，两者才会发生碰撞，所以这里可以通过二分直接求出来。

查看代码

 int n, L, tot;
PII p[maxn];

struct Node {
  int w, x, d;
} a[maxn];

void solve() {
  cin >> n >> L;
  for (int i = 1; i <= n; i++) cin >> a[i].w >> a[i].x >> a[i].d, tot += a[i].w;
  // 根据x排序，求出相对位置
  sort(a + 1, a + 1 + n, [&](Node x, Node y) { return x.x < y.x; });
  // 根据t排序，求出T
  for (int i = 1; i <= n; i++)
    p[i] = {a[i].d == 1 ? L - a[i].x : a[i].x, a[i].d};
  sort(p + 1, p + 1 + n);
  int sum = 0, T = 0;
  for (int i = 1, pl = 1, pr = n; i <= n; i++) {
    T = p[i].first;
    // 如果当前时刻是往左走的牛到达终点，那么就是左端点的牛到达终点
    sum += p[i].second == -1 ? a[pl++].w : a[pr--].w;
    if (sum * 2 >= tot) break;
  }
  // 根据T二分统计答案
  int ans = 0;
  vector<int> pos;
  for (int i = 1; i <= n; i++) {
    if (a[i].d == -1) {
      ans += pos.end() - lower_bound(all(pos), a[i].x - 2 * T);
    } else {
      pos.emp(a[i].x);
    }
  }
  cout << ans << endl;
}

 

433. P5839 [USACO19DEC]Moortal Cowmbat G 【k个字符相同 + 直接DP】

题意：给你一个字符串S，需要修改一些位置，使得S中每个字符连续出现次数大于等于K，求出最小修改花费。

转移方程：\(F[i] = min(F[j], cost(i, j,  c)) 其中 j<=i-k\)

可以通过前缀min维护，总复杂度 \(O(n*m)\)

这道题的思想在于，定义f[i]为[1,i]合法的最小花费，那么末尾一定有一个同一字符、长度大于等于k的子串，那么根据这个子串转移就可以了，通过前缀min可以优化，足够通过此题。

 

434. P5851 [USACO19DEC]Greedy Pie Eaters P 【思维 + 区间DP】【题解】

麻了，没看出能够区间DP。。。。。多少有点菜。

 

435. P5852 [USACO19DEC]Bessie's Snow Cow P【数据结构 + 树上染色 + set染色去重】

题意：两种操作，①对一个子树染上颜色c，对于染上过c的，就不染；②查询子树中sum(x)之和，sum(x)代表x节点有多少种颜色。

首先跑出dfs序，之后就可以像珂朵莉树一样维护维护子树区间染色 - 这样就可以防止重复计数。

然后考虑怎么维护答案：

对于查询子树x，贡献有两种来源

（1）x的祖先染了某种颜色，导致x的子树也有这种颜色 - 树状数组维护每个节点从祖先中继承了多少种颜色，这个可以区间加减来维护，单点查询

一开始还想着树链剖分去找x的祖先有多少种颜色，不如对x的操作的时候就对x的子树维护一下数据，复杂度还低一点。。。

（2）x的某个孙子的子树染了某种颜色 - 树状数组维护每个节点对祖先贡献了多少答案，比如说x的子树染上c，那么x对祖先贡献(r-l+1)。

整体复杂度:\(O(n*logn)\)

 

 

436. P6006 [USACO20JAN]Farmer John Solves 3SUM G【预处理 + 思维 + 区间DP】

题意：给你一个数组长度小于等于5000，1e5次询问，每次询问区间(l,r)内有多少对(i,j,k)满足\(a_i+a_j+a_k=0\)。

tm这怎么想到区间DP啊。。。

 

437. P6009 [USACO20JAN]Non-Decreasing Subsequences P【cdq分治 / 优化矩阵乘法】

（1）做法一：矩阵乘法优化 + 技巧

首先写出DP递推式，定义F[i][j]为考虑到前i位，最后以j结尾的合法序列答案数。

那么有 \(F[i][j] = \sum^j_k F[i-1][k]\)。很显然可以矩阵转移DP，但是直接做的话复杂度太高了，式子：

写成矩阵就是

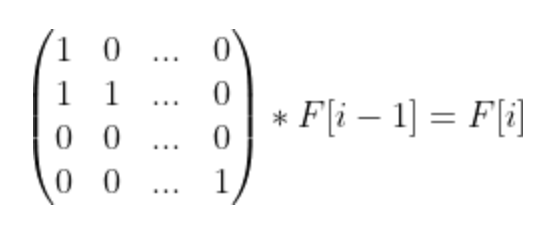
即：\(F[i] = A[i]*A[i-1]*...A[1]*F[0]\)

我们现在看看答案的式子是怎么样的：

\(\begin{align*}ans &= \begin{pmatrix}\begin{pmatrix}1,1 ,.... ,1\end{pmatrix}* \prod^r_l T *\begin{pmatrix}1\\0\\...\\0\\\end{pmatrix}\end{pmatrix} \\ &= \begin{pmatrix}\begin{pmatrix}1,1 ,.... ,1\end{pmatrix}* \prod^{r}_1T\end{pmatrix} *  \begin{pmatrix}\prod^{l-1}_1 T^{-1}*\begin{pmatrix}1\\0\\...\\0\\\end{pmatrix}\end{pmatrix}\end{align*}\)

公式左侧是：\(A[r]*A[r-1]*..*A[1]\) 右侧是：\(A^{-1}[1]*...*A^{-1}[l-1]\)。

矩阵乘法本来复杂度是：\(O(k^3)\)的，但是因为矩阵\(A_i\)非0的位置只有：\(O(k)\)个，所以预处理\(T_i、T^{-1}_i\)的复杂度可以变成：\(O(n*K^2)\)。

但是如果直接拿\(T_i、T^{-1}_i\)矩阵去查询，矩阵非0位置有：\(O(k^2)\)，复杂度还是：\(O(q*k^3)\)啊，那么还是TLE啊。。。

我们观察上面的式子，可以把左侧的括号提前预处理算出来，那么是一个 \(O(k)\)的行向量，右侧的括号提前算出来，是一个\(O(k)\)的列向量。

查询到时候直接 \(O(k)\) 求和即可，所以复杂度是： \(O(q*k)\)的。

还有:\(T^{-1}_i\)怎么算？我们先看看\(A_i\)的逆矩阵\(A^{-1}_i\)。因为\(A_i\)结构比较简单，可以手算出逆矩阵，方法就是：形成一个n*(2n)的一个矩阵，左侧是\(A_i\)，右侧是单位矩阵，通过行初等变换把左侧变成单位矩阵，右侧就是逆矩阵。 

复习：行初等变换包括:①交换两行，②某一行乘上某个常数，③第i行加上c*第j行，其中c是一个常数。

总结：没想到一个简单的预处理+计算顺序的变换可以极大降低复杂度。

查看代码

 int n, a, k, q; 
int inv2 = (mod + 1) / 2;
int mat[30][30], imat[30][30];
int pre[maxn][30], ipre[maxn][30];

int add(int x, int y) {
  x += y;
  return x >= mod ? x - mod: x;
}

int sub(int x, int y) {
  x -= y;
  return x < 0 ? x + mod : x;
}

int mul(int x, int y) { return 1ll * x * y % mod; }

void solve() {
  cin >> n >> k;
  // init
  ipre[0][0] = 1;
  for (signed i = 0; i <= k; i++) mat[i][i] = imat[i][i] = pre[0][i] = 1;
  // 计算每个位置的pre、ipre
  for (signed i = 1; i <= n; i++) {
    cin >> a;
    for (signed r = a; r >= 0; r--)   // 往左侧添加A[r]*A[r-1]...A[1] 
      for (signed c = 0; c <= k; c++) 
        mat[a][c] = add(mat[a][c], mat[r][c]);
    for (signed r = 0; r <= k; r++)  // 往右侧添加iA[1]*...*iA[l-1]
      for (signed c = 0; c <= a; c++)
        imat[r][c] = sub(imat[r][c], mul(inv2, imat[r][a]));
    for (signed c = 0; c <= k; c++)   // 左侧是行向量(1,1,1,1.....)
      for (signed r = 0; r <= k; r++)
        pre[i][c] = add(pre[i][c], mat[r][c]);
    for (signed r = 0; r <= k; r++)  // 最右侧是列向量(1,0,0,0 ....)
      ipre[i][r] = imat[r][0];
  }
  // 回复询问
  cin >> q;
  while (q--) {
    signed l, r, ans = 0;
    cin >> l >> r;
    for (signed i = 0; i <= k; i++)
      ans = add(ans, mul(pre[r][i], ipre[l - 1][i]));
    cout << ans << "\n";
  }
}

（2）cdq分治 - 看洛谷题解去吧

 

438. Laser【2022HDU多校 + 思维题】 

题意：一个镭射炮可以发出米字型的激光，位于 \( (x,y)\) 的镭射炮可以击杀 \((x+k,y)、(x,y+k)、(x+k,y+k)、(x+k,y-k)\) 的敌人。让你判断1个镭射炮是否可以击杀所有敌人。

首先随意在数组中找一个点A，把镭射炮放在这个点上面，如果ok，那么就合法。否则我们可以找到一个点B，A和B不满足米字关系。为了让A、B同时被击杀，只有12个点符合要求，check一下这12个点即可。

第i个点的坐标为：\((x_i,y_i)\)，只需要满足

• \((x_i+y_i)=(x_s+y_s)\)
• \((x_i-y_i)=(x_s-y_s)\)
• \(x_i=x_s\)
• \(y_i=y_s\)

这4个条件之一的任意一个，就可以被击杀。

为了让A被击杀，我们选择1个条件，然后为了让B被击杀，我们选择剩下3个条件，共3*4种选择，所以只有12个点合法，暴力check一下就行了。

 

439. P6024 机器人 - 洛谷【期望 + 贪心】

首先得到期望递推公式，像DP递推式一样：\(F[i]=F[i-1]+w[i]+(1-p_i)*F[i]\) => \(F[i] = \frac{F[i-1]+w[i]}{p_i}\)

理解：第i个任务执行必须花费\(w[i]+F[i-1]\)元，如果失败了，还会花费\(F[i]\)元，两者组成了\(F[i]\)。

这种题一眼就是贪心排序。

然后假设现在确定a、b两个任务的顺序.

假设先b后a：\(F[a]=\frac{F[i-2] + w_b + p_b*w_a}{p_a*p_b}\)

假设先a后b：\(F[b]=\frac{F[i-2] + w_a + p_a*w_b}{p_a*p_b}\)

排序的时候拿这两个东西比较一下就行了。

这道题重点在于推出第一个递推式子，然后得到相邻排序的关系。

 

440. P6026 餐馆【概率推导 + 思维】

出题人一开始是找规律，后面貌似有人给出了EG的推导方式(看不懂)。

 

441.P6028 算术 - 洛谷【推式子 + 数学 + 调和级数 + 除法分块】

转换为调和级数求和。。。然后就不会了

tm的，出题人搞心态，用了一个神奇的式子来求调和级数的前缀和。 - 当然不是准确的，而是精度有问题的。 - 所以出题人精度才放那么松。

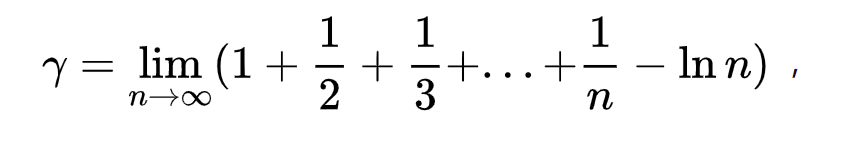
所以：\(\sum^n_{i=1}\frac{1}{i} ≈ y+lnn\)

其中欧拉常数 ：\(γ≈0.57721 56649 01532 86060 65120 90082 40243 10421 59335\)

然后也不太知道正确性，但是近似可能可以这样近似。

然后调和级数还有一些结论：

比如这个：\( \lim_{n\rightarrow ∞} (\frac{1}{n+1}+...+\frac{1}{n+n}) = ln2\)

说明调和级数以 \(ln2\) 的增长速度缓慢增长。

 

442. C. DFS Trees 【图论 + DFS返祖边 + 最小生成树MST + 树上差分】

神奇的是，这一道题跟MST居然没什么关系。俺一直围绕着边权分析来分析去，最后还是做不出来。

思路：首先第一步求出MST，明显，只要dfs(x)不走那些不在MST上的边即可。那么怎么才不走不在MST上的边呢？根据dfs的一些知识，dfs过程中不走一条边，那么这条边一定是返祖边。而 \((u, v)\) 作为一条返祖边的话，要么u是v的祖先，要么v是u的祖先。

难点：我们怎么保证u是v祖先？或者v是u祖先？（呃，这也是我不会的地方）

• 以u为树根，v的子树中的所有节点(包括v自身)开始DFS，那么v一定是u的祖先。
• 以v为树根，u的子树中的所有节点(包括u自身)开始DFS，那么u一定是v的祖先。

那么就是在MST上面对非子树加1，仍然保持为0的节点，dfs(x)出来就是一棵MST。

启发：没想到这个简单的树上差分做懒标记还能做子树加减！！！pushdown之后就是真正的值啦。

代码：【LINK】

顺便说一下这一场的B题啊，B. Difference Array【差分数组 + 暴力优化】【题解】

做到时候想到差分就是a[i]-a[i-1]，所以应该复杂度只跟值域有关系什么的，而且0会很多，所有暴力优化了一下就过了。 - 只要从势能的角度分析就对了。

 

443. K - DOS Card 【带状态的线段树来维护简单区间DP / 广义矩阵优化DP】

题意：定义一个匹配对(i,j)其中i<j的权值是：\(a_i^2-a_j^2\)，每次询问一个区间\([l,r]\) ，让你选出a、b、c、d, 把他们组成两个匹配对，同时权值之和最大。

正解：线段树向上pushup的时候维护状态转移。 - 一眼代码就懂了。【LINK】

这种线段树很常见，可是比赛就是没想到啊。。。反而是想到了DP+广义矩阵优化。其实拐个弯就是正解了，我是sb。【没有AC的解法？LINK】

WA了而不是TLE我十分不服，反正我对拍了200组数据没出锅。。。烦死了。

定义6个dp的状态(代码里面有写)，然后利用广义矩阵乘法进行DP转移，可以用线段树做区间询问，只是常数十分巨大。

卧槽，我发现转移的矩阵是十分空的，有很多无用的格子。

以后凡是用矩阵优化的DP，多次询问求解的DP，我都第一时间想一下能不能直接用线段树来转移。

TM越想越气啊，为什么DP只有6个状态，我都没想到用线段树直接转移啊。好烦啊。

 

 

444. Link with Nim Game 【NIM博弈 + 思维】

题意：nim博弈，输家会选择策略让比赛轮数尽可能多，赢家会让比赛轮数尽可能少，求出最后的比赛轮数。同时在满足上面要求的情况下，输出Alice第一手能有多少种选择方案。

思路：先对a数组求一遍异或和，确定alice是必胜还是必败。

然后我们给出一个结论：输家一定可以选择一个石堆，从中取出一个石子，然后下一步，赢家最多只能取一个石子。

有了这个结论，我们可以轻松的知道，如果先手必败的话，那么轮数就是 \(sum a_i\) 。

考虑证明这个结论：

  因为必败的时候，异或和为0，设输家为Alice，Alice从石堆\(A\)中取出1个石子（假设石堆A的石子数量：?????10...0，即设lowbit为b），那么取完一个石子之后，a数组异或和变成：...000011111(后面连续b个1)。 - 这一步可以自己思考一下，验证一下。

  下一步，先手为了让异或和重新变成0，即，Bob会选择一个石堆\(B\)：第 \(b\) 位为 \(1\) 。 - 解释： 因为选择的石堆需要满足：\((a_i > a_i \oplus S)\) 其中S是所有石堆异或和。那么这个条件显然可以得到，\(a_i\) 的第 \(b\) 位一定是 \(1\) 。赢家需要取的石子数量为：\(B - B \oplus S\)。

  但是，这样并没有保证赢家一定只取一个石子，除非 \(B\)满足\(lowbit(B)=b\)。 - 解释：当B的最低位是b时，异或完之后相减，恰好等于1。

  也就是说，存在这么一个原则：输家Alice选的石堆A，假设\(lowbit(A)=b\)，使得不存在另一个石堆B满足：\((B \& (1 << b)) \&\& (B \& (1 << b) - 1)\) - 式子的解释【即B的第b位是1，但b不是lowbit(B)】

  如果不存在这么一个石堆，那么一定存在某个石堆B，如果B的第b位为1，那么一定有lowbit(B)=b成立。因为异或和为0，这一位必须抵消掉。

  输家只需要按照这个原则取石子，那么赢家只能被迫选1个石子，大概就是这么理解：输家从A石堆中取了1个石子，并且强迫赢家从B石堆中取一个石子，同时\(lowbit(A)=lowbit(B)\)。

然后根据上面这个原则，输家的先手有多少种可能选择的方案数就可以算出来了。

查看代码

 #define lowbitid(x) (__builtin_ctzll(x))       // count tail zero
int n, cnt[50], a[maxn];

void solve() {
  cin >> n;
  ll sum = 0, res = 0;
  for (int i = 1; i <= n; i++) 
    cin >> a[i], res ^= a[i], sum += a[i];
  if (res) {
    ll mx = 0, mxcnt = 0;
    for (int i = 1; i <= n; i++) {
      int tmp = res ^ a[i];
      if (tmp >= a[i]) continue;
      if (mx < a[i] - tmp) {
        mx = a[i] - tmp, mxcnt = 1;
      } else if (mx == a[i] - tmp) {
        mxcnt++;
      }
    }
    cout << sum - mx + 1 << " " << mxcnt << '\n';
  } else {
    me(cnt, 0);
    for (int i = 1; i <= n; i++) 
      if (a[i]) cnt[lowbitid(a[i])]++;
    ll mxcnt = 0;
    for (int i = 0; i < 31; i++) {
        for (int j = 1; j <= n; j++) {
            ll t2 = (1ll << (i + 1)) - 1;
            ll t0 = (1ll << i);
            ll t1 = (1ll << i) - 1;
            // 注意：不能直接用 a[j] & t2
            if ((a[j] & t0) && (a[j] & t1)) {
                cnt[i] = 0;
                break;
            }
        }
        mxcnt += cnt[i];
    }
    cout << sum << " " << mxcnt << '\n';
  }
}

 

445：Equipment Upgrade - HDU 7162【期望 + DP思维 + 使用渐进法/贡献法求期望】

题意：一件武器有[0,n]这n+1个等级，每次从i级升级消耗\(c_i\)金币，有\(p_i\)的概率升级成功，也有概率掉级，掉成i-j的概率是：

让你求从0到n的期望消耗金币。

思路：我一开始是直接设计状态F[0]表示从0级升级到n的期望消耗金币，但是式子是这样的：\(F[i]=c_i + p_i*F[i+1] + (1_p_i)*(后面一坨掉级)\)

这个i+1让我很不好办啊。。。使得这个DP式子形成了一个环。。虽然这在期望题十分常见，但是我今天转换了一下思路，重新设计DP状态。

定义：\(F[i]\)表示从i级提升1级到i+1的期望消耗金币。这样，我们的转移式子就不带环了。

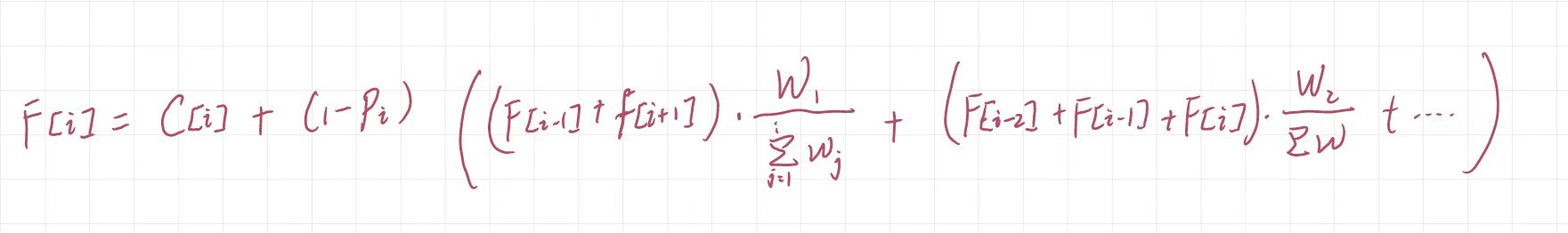
化简一下变成：后面一坨可以用分治NTT求解，然后注意细节就行了。

查看代码

 #pragma optimize(3, "-Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define ispow2(x) (!(((x)-1) & (x)))
#define lowbit(x) (x & (-x))
#define mosbit(x) (1 << (63 - __builtin_clzll(x)))
#define lowbitid(x) (__builtin_ctzll(x))       // count tail zero
#define mosbitid(x) (63 - __builtin_clzll(x))  // count lead zero
// 使用__builtin_popcount的时候，必须注意是否使用longlong
#define ll long long
#define ull unsigned long long
#define lld long double
#define mp make_pair
#define me(a, b) memset(a, (ll)(b), sizeof(a))
#define emp emplace_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define all(x) (x).begin(), (x).end()
#define fi first
#define se second
#define ls (ro << 1)
#define rs (ls | 1)
#define mseg ((l + r) >> 1)
const int maxn = 5e5 + 7, maxm = 1e6 + 11, inf_int = 0x3f3f3f3f;
// 注意，inf_int < 2^30, (1<<31)已经超了int
const ll inf_ll = 0x3f3f3f3f3f3f3f3f;

const ll mod = 998244353;

ll qpow(ll x, ll y) {
  ll r = 1;
  for (; y > 0; y >>= 1, x = (x * x) % mod)
    if (y & 1) r = (r * x) % mod;
  return r;
}

namespace NTT {
int inv_n, ntt_n, revid[maxn];
int EX2(int n) { return 1 << (32 - __builtin_clz(n)); }
int reduce(const int &a) { return a + ((a >> 31) & mod); }
void initNTT(int n) {
  ntt_n = EX2(n);
  for (int i = 1; i < ntt_n; ++i)
    revid[i] = (revid[i >> 1] >> 1) | (i & 1 ? ntt_n >> 1 : 0);
  inv_n = qpow(ntt_n, mod - 2);
}
void ntt(int *a, int opt) {
  for (int i = 1; i < ntt_n; ++i)
    if (revid[i] < i) swap(a[i], a[revid[i]]);
  for (int mid = 1; mid < ntt_n; mid <<= 1) {
    const int gn = qpow(3, (mod - 1) / mid / 2);
    for (int i = 0; i < ntt_n; i += (mid << 1)) {
      int gk = 1;
      for (int j = 0; j < mid; j++, gk = (ll)gk * gn % mod) {
        int tmp = (ll)a[i + j + mid] * gk % mod;
        a[i + j + mid] = reduce(a[i + j] - tmp);
        a[i + j] = reduce(a[i + j] + tmp - mod);
      }
    }
  }
  if (opt == 1) return;
  reverse(a + 1, a + ntt_n);  // 反转后 n - 1 个元素
  for (int i = 0; i < ntt_n; ++i) a[i] = (ll)inv_n * a[i] % mod;
}
};  // namespace NTT
using namespace NTT;

// 多项式乘法， a是n-1次的，b是m-1次的，即[0:n-1]共n个数
void poly_mul(int *const a, int *const b, int n, int m, int *c) {
  static int ta[maxn], tb[maxn];
  initNTT(n + m);  // 必须每次清零
  for (int i = 0; i < ntt_n; ++i) ta[i] = i < n ? a[i] : 0;
  for (int i = 0; i < ntt_n; ++i) tb[i] = i < m ? b[i] : 0;
  ntt(ta, 1), ntt(tb, 1);
  for (int i = 0; i < ntt_n; ++i) c[i] = (ll)ta[i] * tb[i] % mod;
  ntt(c, -1);
}

int n, f[maxn], c[maxn], w[maxn];
int tmp[maxn], sf[maxn], p[maxn];

void cdq_ntt(int l, int r) {
  if (l == r) {
    if (l == 0) {
      sf[0] = f[0] = c[0];
    } else {
      f[l] = 1ll * ((1ll * sf[l - 1] * w[l]) % mod + f[l]) % mod;
      f[l] = 1ll * f[l] * ((mod + 1ll - p[l]) % mod) % mod;
      f[l] = (1ll * f[l] * qpow(w[l], mod - 2) % mod + c[l]) % mod;
      f[l] = (1ll * f[l] * qpow(p[l], mod - 2)) % mod;
      sf[l] = (1ll * sf[l - 1] + f[l]) % mod;
    }
    return;
  }
  int mid = (l + r) >> 1;
  cdq_ntt(l, mid);
  poly_mul(w, f + l, r - l, mid - l + 1, tmp);
  int len = mid - l + 1;
  for (int i = mid + 1, j = 0; i <= r; i++, j++) 
    f[i] = (f[i] + mod - tmp[len + j - 1]) % mod;
  cdq_ntt(mid + 1, r);
}

void solve() {
  cin >> n;
  ll inv100 = qpow(100, mod - 2);
  for (int i = 0; i <= 3 * n; i++) w[i] = tmp[i] = f[i] = sf[i] = 0;
  for (int i = 0; i < n; i++)
    cin >> p[i] >> c[i], p[i] = (1ll * p[i] * inv100) % mod;
  for (int i = 1; i < n; i++) cin >> w[i], w[i] = ((ll)w[i] + w[i - 1]) % mod;
  cdq_ntt(0, n - 1);
  cout << sf[n - 1] << '\n';
}

int main() {
  ios_fast;
  int TEST = 1;
  cin >> TEST;
  while (TEST--) solve();
}

/*

*/

 

446：A-Array_"蔚来杯"2022牛客暑期多校训练营6【构造 + 思维 + 哈夫曼树 + 数组倒数之和小于等于 1/2】

题意：给一个长度为n的数组a，要求你构造一个数组c，使得数组c无限循环之后，对于每一个长度为\(a_i\)的区间，都有i出现。

难点在于怎么使用：\(\sum \frac{1}{a_i} \le \frac{1}{2}\)。

构造的思路：考虑寻找小于等于每个数的最大的2的次幂（最高位）作为该数的周期。将最大的周期定为 m 。然后从小到大排序，依次将每个下标按周期填入。剩余的空白位置直接填1。

正是因为题目给定的条件，所以保证了以2的次幂为周期，是保证可以放进数组的。

查看代码

 const int M = (1 << 18);  // 没有超过1e6即可
int n, b[maxn], cur;
PII a[maxn];

void solve() {
  cin >> n;
  for (int i = 1; i <= n; i++)
    cin >> a[i].fi, a[i].se = i, a[i].fi = mosbit(a[i].fi);
  sort(a + 1, a + 1 + n);
  cur = 0;
  for (int i = 1; i <= n; i++) {
    while (b[cur]) cur++;
    for (int j = cur; j < M; j += a[i].fi) b[j] = a[j].se;
  }
  cout << M << endl;
  for (int i = 0; i < M; i++) cout << max(1, b[i]) << " ";
  cout << endl;
}

 

 

447: I-Line_"蔚来杯"2022牛客暑期多校训练6【高维物体在二维平面上投影 + 要求每一维每一条线上恰好D个点】

投影是比较简单的，但是我们还要保证每一条线只能恰好D个点。。。

 

448：F. Bags with Balls【第二类斯特林数 + k次幂转为k的下降幂】【题解】

题意：求解式子 \( \sum^n_{i=0} a^i * b^{n-i} * C(n,i) * i^k\)。其中 a+b, n<=998244352。a为m中奇数数量，b为偶数数量

会点第二类斯特林数的人，可以想到把这个 \(i^k\) 转成下降幂的形式： \(x^k = \sum^k_{i=0} S_2(k, i) * x^{\underline{i}}\) 

然后上面那个式子变成（已经交换求和号）：

\( \sum^k_{l=0} S_2(k, l) \sum^n_{i=0} a^i*b^{n-i}*C(n,i)*i^{\underline{l}}\)

实际上，\( i^{\underline{l}} = i*(i-1)*...*(i-l+1)\) 和 \(C(n,i)=\frac{n!}{i!*(n-i!)}\) 有一项共同的\(i\)，可以抵消掉，

即 \(C(n, i)*i^{\underline{l}} = n * C(n-1,i-1) * (i-1)^{\underline{l-1}}\)。所以式子变成：

\( \sum^k_{l=0} S_2(k, l) \sum^n_{i=0} a^i*b^{n-i}* n *  C(n-1,i-1)*{(i-1)}^{\underline{l-1}}\)

又因为 负数是没有阶乘的，\(C(n-1,0-1)\)是没意义的，所以 \(i\) 需要从1开始求和，我们不妨直接让n-1，式子变成：

\( \sum^k_{l=0} S_2(k, l)  \sum^{n-1}_{i=0} a^{i+1}*b^{n-1-i}* n *  C(n-1,i)*i^{\underline{l-1}}\)  [a的次幂从i变成i+1,而且中间多了一项乘积n]

那么我们现在可以看到化简前后式子的递推关系了：

\( \sum^k_{l=0} S_2(k,l)* F[n][l] = \sum^k_{l=0}S_2(k,l)* n*a*F[n-1][l-1] \) ，且根据题意或者根据二项式定理有 \(F[n][0]=(a+b)^n\) 

即： \(F[n][l] = a^l*(n^{\underline{l}})*(a+b)^{n-l}\)  // 这里我一开始以为递推：\(F[n][l]=(n*a)^l*(a+b)^{n-l}\)。。，。结果错了1年，以后不许这么傻逼了。

所以可以先\(O(k^2)\)预处理第二类斯特林数，然后每次都：\(O(logn+k)\)的复杂度去统计答案。

查看代码

 int S2[2007][2007];

void initS2() {
  S2[0][0] = 1;
  for (int i = 1; i <= 2000; i++) {
    for (int j = 1; j <= i; j++) {
      S2[i][j] = (S2[i - 1][j - 1] + 1ll * j * S2[i - 1][j]) % mod;
    }
  }
}

int n, m, k;

ll qpow(ll x, ll y) {
  ll r = 1;
  for (; y > 0; y >>= 1, x = (ll)x * x % mod)
    if (y & 1) r = (ll)r * x % mod;
  return r;
}

void solve() { 
  cin >> n >> m >> k;
  ll ans = 0, a = (m + 1) / 2, F = qpow(m, n), invm = qpow(m, mod - 2);
  for (int l = 0; l <= k && l <= n; l++) {  // l不仅要小于等于k，还要小于等于n
    ans = (ans + 1ll * S2[k][l] * F % mod) % mod;  
    F = (F * invm % mod * (n - l) % mod * a % mod) % mod; 
    // 根据递推，是乘 n-l 而不是 n
  }
  cout << ans << endl;
}

 

449：E. Swap and Maximum Block【二进制交换Block / 思维 / 线段树求区间最大和】

题意：每次让index xor (1<<k)，操作累计下去，每次操作完询问整个数组的区间最大和。

一眼就知道应该像线段树一样操作，可是没想清楚，导致没想到对的模型上面去。 - 我们知道一个位是1，就相当于交换线段树上面的两个节点。

但是如果没有合理的建模方法，就无法得到复杂度正确的做法。

从线段树的底向上考虑，最后一层 \(2^n\)个节点，只有1种状态，即原来数组的状态；倒数第2层\(2^{n-1}\)个节点，有2种状态，即原来合并的状态，以及该位是1（交换左右儿子）的状态。依次类推。我们最后第一层有1个节点，一共\(2^n\)种状态，刚好对应\(2^n\)个答案。

这道题的图形化表示是这样的：（反正很多节点都是共用的，空间复杂度滚动一下可以达到：\(O(2^n)\), 时间复杂度：\(n*2^n\)）

 

 

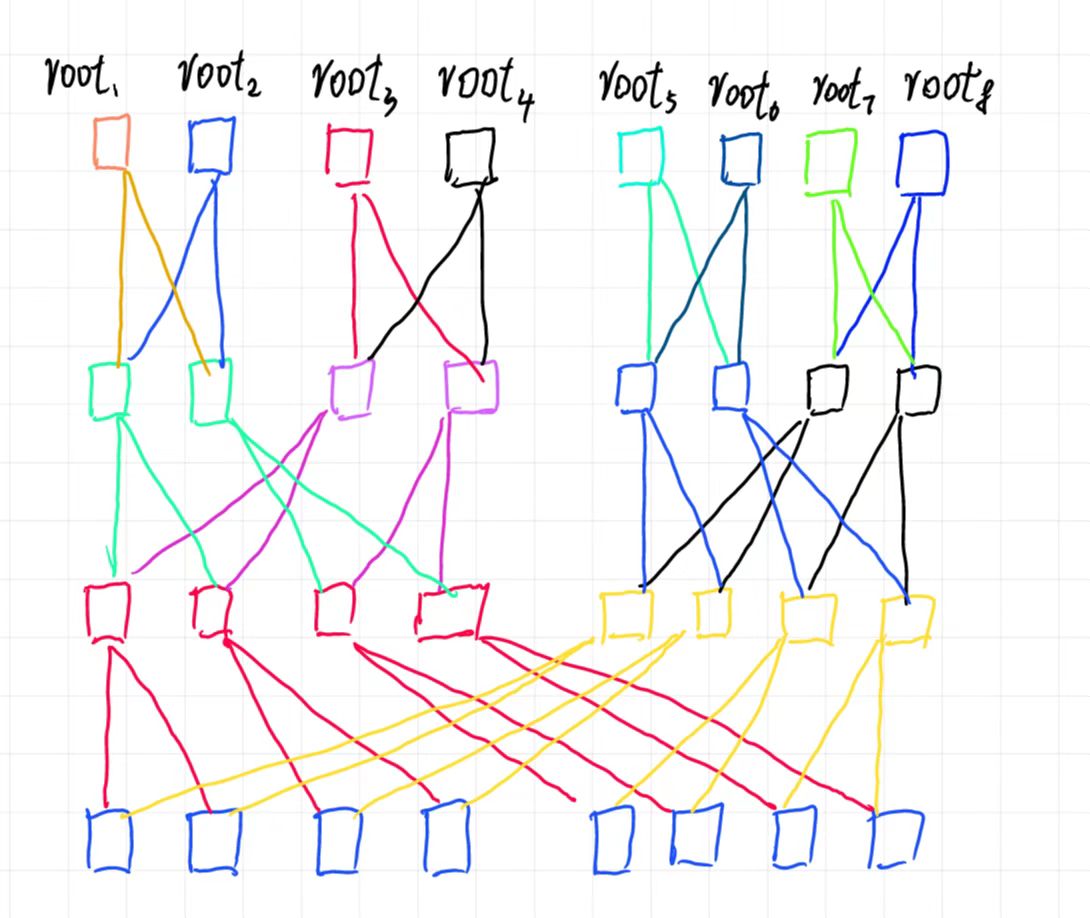
450： [CF1713E] Cross Swapping【并查集计算0、1解 + 贪心 + 思维】

思路：做题的时候，发现：

• 如果G[i][j]<G[j][i]，那么i和j要么同时换，要么同时不换。即：x[i]^x[j]=0
• 如果G[i][j]>G[j][i]，那么i和j要么i换j不换，要么i不换j换。x[i]^x[j]=1
• 否则没有限制

可以看到，就是求解一系列的异或方程，但是因为题目对比的是字典序，即在满足前面的方程的情况下，后面的方程尽量满足。

一开始还蠢蠢地去想高斯消元。。。。但是这类划分集合就可以解地方程直接上并查集就好了。

我不会像其它人一样用正负表示0、1权值，只好用并查集懒标记来计算每个点的权值了。【因为并查集的根节点的懒标记永远是空的，传递标记的时候只会记录路径上的标记，所以不用担心重复接收了某个标记】

查看代码

 int n, G[1001][1001], Lock[1001];
int fa[1005], w[1005], tg[1005];
 
void Swap(int x) {
  for (int i = 1; i <= n; i++) swap(G[i][x], G[x][i]);
}
 
int Find(int x) {
  if (x == fa[x]) return x;
  int tfa = fa[x];
  fa[x] = Find(fa[x]);
  tg[x] ^= tg[tfa], w[x] ^= tg[tfa];
  return fa[x];
}
 
void solve() {
  cin >> n;
  for (int i = 1; i <= n; i++) fa[i] = i, w[i] = tg[i] = 0;
  for (int i = 1; i <= n; i++)
    for (int j = 1; j <= n; j++) cin >> G[i][j];
  for (int i = 1; i <= n; i++) {
    for (int j = i + 1; j <= n; j++) {
      if (G[i][j] == G[j][i]) continue;
      int fx = Find(i), fy = Find(j);
      if (fx == fy) continue;
      fa[fx] = fy;
      if ((G[i][j] < G[j][i] && w[i] != w[j]) ||
          (G[i][j] > G[j][i] && w[i] == w[j])) w[fx] ^= 1, tg[fx] ^= 1;  // w[fx]也要 ^=1
    }
  }
  for (int i = 1; i <= n; i++) {
    Find(i);
    if (w[i]) Swap(i);
  }
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
      cout << G[i][j] << " ";
    }
    cout << endl;
  }
}

 

 

451：Melborp Elcissalc【思维 + 计数DP + 前缀和相等 = 模除为0 = 整除(多添加一个维度)】

题意：数组a长度为n，每个位置能够使0~K-1的整数。如果数组a的一个区间和能被K整除，那么他是一个好区间(要求非空)。请问有多少种构造方法使得数组a恰好有T个好区间。

整除K，不仅仅可以用模除为0的思想，还可以用前缀和的思想。即 suma[j]=suma[i]，那么[j+1,i]就是一个好区间。

又因为数组a对应了它的一个前缀和数组suma，我们直接考虑suma的每一位是0~k-1的哪一个数字（模K意义下的）。

我们可以从这个角度进行DP。

定义: \(dp[i][j][k]\)为填充了\(0....i\)这i+1个数，填充了a数组种的 j 个位置，已经有k个好区间的方案数。

转移就是：

① 考虑充填L个0，但是一开始就有1个0是固定的，所以转移为：\(dp[0][j+L][k+C(L+1,2)] += C(j+L,L)*dp[0][j][k]\)

② 如果是大于0的数，正常插入即可：\(dp[i][j+L][k+C(L, 2)] += C(j+L,L) * dp[i-1][j][k]\)

细节：别忘了乘上C(j+L,L)把L个数字i插入j+L个位置里面。- 这很关键。

查看代码

 int n, k, t, C[66][66], dp[64][65][65 * 32 + 1];

int add(int x, int y) {
  x += y;
  return x >= mod ? x - mod : x;
}

void initC() {
  C[0][0] = 1;
  for (int i = 1; i < 66; i++) {
    C[i][0] = C[i][i] = 1;
    for (int j = 1; j < i; j++) C[i][j] = add(C[i - 1][j - 1], C[i - 1][j]); 
  }
}

void solve() {
  cin >> n >> k >> t;
  initC();
  for (int l = 0; l <= n; l++) 
    dp[0][l][C[l + 1][2]] = 1;
  for (int i = 1; i < k; i++) {
    for (int j = 0; j <= n; j++) {
      for (int l = 0; l + j <= n; l++) {
        for (int r = 0; r + C[l][2] <= t; r++) {
          dp[i][j + l][r + C[l][2]] = add(dp[i][j + l][r + C[l][2]], (ll)C[l + j][j] * dp[i - 1][j][r] % mod);
        }
      }
    }
  }
  cout << dp[k - 1][n][t] << endl;
}

 

 

452：D. Double Pleasure【状压 + 数位DP】

题意：定义一个数为pleasure数，当且仅当它满足：gcd(mul(a), a)!=1。其中mul(a)表示a的数位乘积。比如mul(134)=1*3*4。每次询问整数区间[L,R]有多少个pleasure数。

十分考察基础的数位DP题目。

很明显，只需要a满足下面5个条件之一就行了：

1. a存在质因子2，同时a有数位2/4/6/8。
2. a存在质因子3，同时a有数位3/6/9。
3. a存在质因子5，同时a有数位5。
4. a存在质因子7，同时a有数位7。
5. a存在数位0。

关键是如何使用状态表示上面这些条件，又如何套用数位DP求解，所以说是一道比较基础的数位DP。

这里记录一下看完别人代码之后的感受。这道题我也是想到了上面的5个条件，但是却不知道该怎么下手。

定义 \(f[len][mask][2][3][5][7][zero]\) 为前面的位考虑完毕，状态为mask，对2、3、5、7的模数分别为a，b，c，d，还剩len长的方案数，zero代表是否有前缀0。也可以简化以下状态：\(F[len][mask][2*3*5*7][zero]\)，因为模除lcm(2,3,5,7)之后，不会丢失模除2、3、5、7的值。

数位DP的状态用于记录前面n-len位的信息，这样想来写代码就有方向一点了。

转移的时候就枚举第len位填什么，01...9。

细节：

① 这道题T=1e4，如果每一次数位dp都memset(dp,-1)的话，会TLE。而且这道题并没有其它限制条件，只有询问[l,r]区间的操作，所以一开始就memset(dp,-1)，后续不需要再memset了，相当于记忆化。（对于每组询问，记忆化的数组是不需要清空的，因为这一题没有额外的约束条件）

② 对于mask来说，当前导0存在的时候，0是不可以更新mask的。

查看代码

 int len, num[20];
const int LCM = 2 * 3 * 5 * 7;
ll dp[20][32][2 * 3 * 5 * 7][2];

ll dfs(int len, int mask, int d, int lim, int zero) {
  if (len == 0) {
    if (zero) return 0;
    if ((mask & 1) && d % 2 == 0) return 1;
    if ((mask & 2) && d % 3 == 0) return 1;
    if ((mask & 4) && d % 5 == 0) return 1;
    if ((mask & 8) && d % 7 == 0) return 1;
    if (mask & 16) return 1;
    return 0;
  }
  if (!lim && -1 != dp[len][mask][d][zero]) {
    return dp[len][mask][d][zero];
  }
  int mx = lim ? num[len] : 9;
  ll ret = 0;
  for (int i = 0; i <= mx; i++) {
    int nmask = mask;
    if (!i) {
      if (!zero) nmask |= 16;  // 这里必须判断!zero，前缀0存在的情况下，0是无效的
    } else {
      if (i % 2 == 0) nmask |= 1; 
      if (i % 3 == 0) nmask |= 2; 
      if (i % 5 == 0) nmask |= 4; 
      if (i % 7 == 0) nmask |= 8; 
    }
    ret += dfs(len - 1, nmask, (d * 10 + i) % LCM, lim & (i == mx), zero & !i);
  }
  if (!lim) dp[len][mask][d][zero] = ret;
  return ret;
}

ll Work(ll x) {
  if (!x) return 0;
  len = 0;
  while (x) num[++len] = x % 10, x /= 10;
  return dfs(len, 0, 0, 1, 1);
}

void solve() {
  ll L, R;
  cin >> L >> R;
  if (L > R) swap(L, R);
  cout << Work(R) - Work(L - 1) << '\n'; 
}

int main() {
  me(dp, -1);  // 初始化1次就好了
  ios_fast; 
  int TEST = 1;
  cin >> TEST;
  while (TEST--) solve();
}

 

453：Matrix and GCD【二维网格 + 扫描线求贡献思想 + 二维子矩阵 gcd + 倍数容斥】

题意：给定一个n*m的二维网格，每个位置是1~n*m中的每个数，且1~n*m排列中每个数只出现一次，求所有子矩阵gcd之和。

思路：考虑枚举gcd，把网格中是gcd倍数的位置置为1，不是gcd倍数的置为0。然后数有多少个子矩阵是全1的。

【怎么数全1矩阵呢？】

我们先找到每一列，每一段的第一个是1的位置，然后从上往下累计高度，用于后续单调栈的计算。

然后找到每一行(假设当前行是Row)，每一连续段1的最开头的位置，然后用单调栈计算第j列到第i列的最低高度，然后这些最低高度求一下和，就是(Row，i)这个点作为右下端点能有多少个子矩阵为全1。 

注意，计算完之后要标记这个格子，避免多次计算。

【然后考虑容斥】

我们刚刚算的是：f[i] = i的倍数组成的子矩阵数量。假设g[i]是gcd为i的子矩阵的数量，那么有: \(f[i]-=g[2*i]+g[3*i]+g[4*i]+....\)。假设\(t=\lfloor\frac{nm}{i}\rfloor\)，那么有 \(f[i*t]=g[i*t]\)。因为除了他自己，没有数是i*t的倍数 - 所以不用容斥就是答案。那么根据上面的定义，可以用埃式筛的方式从上往下递推出来。复杂度\(O(n*lnn)\)。 - 这个没有重复枚举的情况 - 注意区分二项式反演的容斥，那个是有C(n,i)种情况重复枚举的，所以使用二项式反演。

查看代码

 struct Node {
  int height, cnt;
} stk[maxn];

int n, m, top, x[maxn], y[maxn], len[1006][1006];
ll f[maxn];

ll calc(int d) {
  for (int i = d; i <= n * m; i += d) len[x[i]][y[i]] = -1;
  for (int i = d; i <= n * m; i += d) {
    if (len[x[i]][y[i]] >= 0 || len[x[i] - 1][y[i]] == -1)
      continue;  // 枚举每一列最顶部的节点，然后往下记录高度
    int cx = x[i], cy = y[i], cnt = 0;
    while (len[cx][cy] == -1) len[cx][cy] = ++cnt, cx++;
  }
  ll ret = 0;
  for (int i = d; i <= n * m; i += d) {
    int cx = x[i], cy = y[i];
    if (len[cx][cy] == 0 || len[cx][cy - 1] > 0)
      continue;  // 枚举最左边的节点，然后往右扫单调栈
    ll tot_sum = 0;
    stk[top = 0] = {-inf_int, 0};
    while (len[cx][cy] > 0) {
      int tmp_cnt = 1;
      tot_sum += len[cx][cy];  // 记得加上
      while (stk[top].height > len[cx][cy]) {
        tot_sum -= 1ll * stk[top].height * stk[top].cnt;
        tot_sum += 1ll * stk[top].cnt * len[cx][cy];
        tmp_cnt += stk[top].cnt;
        top--;
      }
      stk[++top] = {len[cx][cy], tmp_cnt};
      ret += tot_sum;         //累加答案
      len[cx][cy] = 0, cy++;  // 记得置0
    }
  }
  return ret;
}

void solve() {
  cin >> n >> m;
  for (int i = 1; i <= n; i++)
    for (int j = 1, a; j <= m; j++) cin >> a, x[a] = i, y[a] = j;
  for (int i = 1; i <= n * m; i++) f[i] = calc(i);
  for (int i = n * m; i; i--)
    for (int j = 2 * i; j <= n * m; j += i) f[i] -= f[j];
  ll ans = 0;
  for (int i = 1; i <= n * m; i++) ans += i * f[i];
  cout << ans << endl;
}

 

454：P4756 Added Sequence 【直线维护凸包 / 李超树】【维护上下凸包模板题】

题意：给定一个长度为2e5的数组a，定义 \(f(i,j)\) 为区间[i,j]的和，每次询问给定一个x，求\( |f(i,j)+(j-i+1)*x|\) 的最大值。其中\(i\ge j\)。

思路：\(原式=|sum(j)-sum(i-1)+(j-i+1)*x|=|(sum(j)+j*x) - (sum(i-1)+(i-1)*x)|\)

如果定义\(g(i)=sum(i)+i*x\)，那么要使得式子最大，一定是一个最大值，一个最小值。 - （因为加了绝对值之后，可以理解为差值的最大值，那么就是最大值减最小值）  - 【不要被题目的\(i\ge j\)迷惑了，它的本质就是最大值-最小值】

而 \(n\)个\(g(i,x)\)函数可以看成是\(n\)条直线，我们维护这n条之间，取得最值就行了。 - 可以使用凸包/李超树实现。

细节：记得全部开longlong，不然溢出。

【另一道维护下凸包的模板题 - P3194 [HNOI2008]水平可见直线】

查看代码

#include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using ll = long long;
const int maxn = 5e5 + 7;
const double eps = 1e-6;

struct Convex {  // 维护凸包
  // 直线按斜率从小到大插入 就是维护下凸包 - 求X=x的最大值
  // 直线按斜率从大到小插入 就是维护上凸包 - 求X=x的最小值
  ll K[maxn], B[maxn], top;  // 斜率，截距
  double X[maxn];
  void init() { top = 0; }
  double calc(ll k1, ll b1, ll k2, ll b2) {  // 两直线交点的x坐标
    return (double)(b2 - b1) / (double)(k1 - k2);
  }
  void insert(ll k, ll b) {  // 插入一条直线
    if (top && K[top] == k && B[top] > b) return ; // 特判
    while (top && K[top] == k && b > B[top]) top--;
    for (; top > 1; top--)
      if (calc(k, b, K[top], B[top]) > X[top]) break;
    ++top, K[top] = k, B[top] = b;
    if (top > 1) X[top] = calc(k, b, K[top - 1], B[top - 1]);
  }
  ll getY(ll x) {  // 返回X=x时，最大/小值 = Y
    if (x <= X[2] && top >= 2) return K[1] * x + B[1];
    if (x >= X[top]) return K[top] * x + B[top];
    int pos = lower_bound(X + 2, X + top, x) - X - 1; // 别忘了-1
    return K[pos] * x + B[pos];
  }
} mx, mn;

int n, m;
ll a[maxn], pre, x;

int main() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++) scanf("%lld", &a[i]), a[i] += a[i - 1];
  for (int i = 0; i <= n; i++) mx.insert(i, a[i]);
  for (int i = n; i >= 0; i--) mn.insert(i, a[i]);
  while (m--) {
    scanf("%lld", &x);
    x = ((x + pre) % (4 * n + 1) - 2 * n);
    pre = (mx.getY(x) - mn.getY(x));
    printf("%lld\n", pre);
  }
}

 

 

455：Online Majority Element In Subarray - LeetCode【数据结构：区间绝对众数 + 以及该众数出现次数】

题意：给定一个数组，每次询问一个区间[l,r]的绝对众数以及它的出现次数，如果没有，返回-1.（绝对众数在区间中出现次数大于(len/2)）

根据摩尔投票法来求区间绝对众数，得到一个二元组(number, count)。这个东西是可以合并的，所以直接在线段树上合并就行了或者直接倍增（常数小）。

但是要计算区间内某个数出现了多少次，就一定要用二分来计数了。

我犯了一个错误：假设区间长度为len，最后投票为num，我一开始以为(len+num)/2就是出现次数。但是这是不对的，因为在计算过程中，绝对众数也有可能会投减票，这样就导致最后数量过少。

查看代码

class MajorityChecker {
public:
    int LIM;
    vector<vector<pair<int, int>>> st; 
    unordered_map<int, vector<int>> pos;
    
    MajorityChecker(vector<int>& arr) {
        LIM = log2(arr.size()) + 1;
        st.assign(LIM, vector<pair<int, int>>(arr.size(), {-1, 0}));
        for (int i = 0; i < arr.size(); i++) 
            st[0][i] = make_pair(arr[i], 1), pos[arr[i]].push_back(i);
        for (int d = 1; d < LIM; d++) 
            for (int i = 0; i + (1 << (d - 1)) < arr.size(); i++)
                st[d][i] = merge(st[d - 1][i], st[d - 1][i + (1 << (d - 1))]);
    }
    
    pair<int, int> merge(pair<int, int> a, pair<int, int> b) {
        if (a.first == -1 || a.second == 0) return b;
        if (b.first == -1 || b.second == 0) return a;
        if (a.first == b.first) return make_pair(a.first, a.second + b.second);
        if (a.second > b.second) return make_pair(a.first, a.second - b.second);
        return make_pair(b.first, b.second - a.second);
    }
    
    int query(int left, int right, int threshold) {
        #define all(x) (x).begin(), (x).end()
        pair<int, int> p = {-1, 0};
        for (int d = LIM - 1, l = left; d >= 0; d--) 
            if (l + (1 << d) - 1 <= right) 
                p = merge(p, st[d][l]), l += (1 << d);
        int cnt = upper_bound(all(pos[p.first]), right) - lower_bound(all(pos[p.first]), left);  // 计算区间绝对众数出现了多少次
        if (cnt >= threshold) return p.first;
        return -1;
    }
};

 

456：Board Game【思维 + 枚举 + 贪心】

题意：你有n（n<=1e9）个士兵，你要把它们分成m(m<=1e7)组，对手是一个魔法师，每一轮由你先手，你操纵所有士兵，每个士兵对敌人造成1点伤害，之后魔法师选择一组士兵，并且杀掉至多k（k<=1e7）个士兵。已知魔法师足够聪明，你要怎么分组才能使得造成的伤害最大？

思路：如果存在一组 k+t 个士兵，那么它等价于一组k个士兵和一组t个士兵。所以我们把所有大于等于k的组拆出来，假设一共有a组k个士兵，剩下的组都是小于k的。从贪心的角度来说，这些小于k的组肯定是越平均越好的，因为魔法师会逮着人数多的组来动手。但是a怎么选择呢？

我们首先看看a的取值范围，a的下界是: \( \max(\lceil\frac{n - (k-1)*m}{k}\rceil, 0) \) - 先让m个组都有k-1个人，然后再把剩下的分配到k个人的组，注意要向上取整。a的上界就是: \(\lfloor\frac{n}{k}\rfloor\) - 就是直接能选就选，把所有人放到k个人的组里面。

刚好上下界相差\(O(m)\)级别，所以直接枚举就行了。【这种题貌似无法通过贪心确定a，但是对于人数小于k的组，却又可以贪心地平均分配】

 

457：P2180 摆石子【思维 + 枚举】

题意：给定一个n<=3e4*m<=3e4的网格，你要把k<=n*m的石子放进去网格，询问最多能有多少个不同的矩形，它的四个点只有1个石子。

细节1：这道题不仅仅要枚举行，还要枚举列。。。。。如果忘记了其中一个，都会被卡掉。

细节2：题目要求四个点只有1个石子，但是要完全放满k个石子，如果有一个格子有两个石子，那么这个格子相当于废掉。

 

457和456都是差不多的思路，如果题目十分抽象，很难直接贪心，然后需要考虑枚举的方式，再贪心计算答案

 

458：P3299 [SDOI2013]保护出题人【通过斜率优化求解式子最值 + 凸包 （不是斜率优化DP，当答案的含义是平面的斜率时，就可以在凸包上二分）】

题目意思好难懂啊：在横坐标上玩植物大战僵尸，一共有n关，第i关中，僵尸的排列是这样的:\(a_i,a_{i-1}..a_1]\)，其中第一个僵尸在\(x_i\)处，第二个僵尸在\(x_i+d\)处，第三个在\(x_i+2*d\)处...(d是题目给定的一个偏移量)，求每一关植物的最小攻击力。 - 注意这道题的时间/速度/坐标是连续的，不是离散的。

理解完题目之后，可以贪心地去想，第i关的最小攻击力要满足 \(y_i \ge \max_{j\le i}\frac{sum_i-sum_{j-1}}{x_i+i*d-j*d} \)。这个式子恰好可以拆分成 点来表示。就是\((x+id,sum_i)\)和\((j*d,sum_{j-1})\)两个点的斜率。我们发现右边这个点就是前0~i-1个点，它们是固定不变的，可以通过凸包来维护。（恰好它们的x坐标又是单调递增的，降低了维护的难度）同时\(x+id\)这个横坐标必然是大于\(j*d\)的，所以可以直接二分答案。

查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)

using lld = long double;
using ll = long long;
const int maxn = 5e5 + 7;

ll n, a[maxn], x[maxn], d;
int stk[maxn], top;

lld slope(int i, int j) {
  return (lld)(a[i] - a[j]) / ((i + 1) * d - (j + 1) * d);
}

lld calcAns(int i, int j) {
  return (lld)(a[i] - a[j]) / (x[i] + i * d - (j + 1) * d);
}

bool better(int i, int j, int k) {  // j better than k
  return calcAns(i, j) > calcAns(i, k);
}

int main() {
  ios_fast;
  cin >> n >> d;
  for (int i = 1; i <= n; i++) cin >> a[i] >> x[i], a[i] += a[i - 1];
  lld ans = 0;
  stk[top = 1] = 0;
  for (int i = 1; i <= n; i++) {
    // 二分切线
    int l = 1, r = top, mid;
    while (l < r) {
      mid = (l + r) >> 1;
      better(i, stk[mid], stk[mid + 1]) ? r = mid : l = mid + 1;
    }
    ans += calcAns(i, stk[r]);
    // 维护凸包
    while (top > 1 && slope(i, stk[top]) <= slope(i, stk[top - 1])) top--;
    stk[++top] = i;
  }
  cout << (ll(ans + 0.5)) << endl;
}

 

459：P2924 [USACO08DEC]Largest Fence G【经典题：动态规划求点数最多的凸包】

题意：给定n=250个点，让你选一些点组成凸多边形，同时点数最多。

这道题有一个很显然的\(O(n^4)\)的DP，朴素DP是无法通过的，但是可以通过一些剪枝卡过去。

• 首先外层循环枚举一个起始点，为了保证每个凸包只被枚举一次，我们先对点按x坐标进行排序，这样只会枚举每个凸包的最左边的点。
• 然后我们枚举了这个点O之后，我们把剩下n-i个点根据O点进行极角排序，这样就是单调的直接转移啦。
• 定义dp[i][j]为当前最后两个节点为i,j的最大答案，如果dp[i][j]=0，直接continue剪枝。
• 然后\(O(n^4)\)因为跑不满所以可以卡过去。【提交记录】

然后这道题有\(O(n^3)\)做法，就是预处理出\(O(n^2)\)条边，根据极角排一下序，然后枚举起点转移即可。

 

460：C. Colorful Tree 2017杭电多校【思维 + 把颜色独立进行统计 + 树上DP】

题意：树上一条路径的权值为不同颜色的数量，请你对n*(n-1)/2条路径的权值求和。

因为是求和，不同颜色之间相互独立。考虑每种颜色的虚树，关键点把原来的树划分成一些没有关键点的块。我们怎么对一种颜色求这些块呢？

其实只需要一次dfs。考虑一个颜色为c的节点x，假设它的子树中，离他最近的，颜色也为c的孙子节点为\(v_1、v_2...\)。那么就会形成一个sz[x]-1-sz[v1]-sz[v2]-....大小的一个块。

但是你可能会想到，对于最顶上的一个块呢？它们是不是dfs递归过程中从上往下第一个遇到的颜色为c的节点啊？我们特判一下，同时用一个数组统计一下就行。【这个代码实现得不错】

 

另一道类似的例题：F. Unique Occurrences

 

461：I. I Curse Myself 2017杭电多校【边仙人掌 + 多路合并 + k小生成树】

题意：求\(\sum^K_{i=1}i*V(i)\) 其中\(V(i)\)是第i小生成树得权值，数据保证每条边最多在一个环上。

先把所有的环拆出来，从大到小排序。然后咧？怎么合并这t个数组得到前k大的和？考虑这个思路【模板--堆维护集合的所有子集中第k大的子集之和】

查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using ll = long long;
const int maxn = 1e5 + 7;

struct Edge {
  int v, w, i;
};

pair<int, int> stk[maxn];
int n, m, k, top, used[maxn], vis[maxn], Case;
vector<vector<Edge>> e;
vector<unsigned> T, W, G;

void merge() {  // 从n*m个数中取出前k大的ai*bj
  sort(W.begin(), W.end(), greater<>());
  if (T.empty()) return T = W, void();
  priority_queue<pair<int, int>> q;
  for (int i = 0; i < W.size(); i++) q.push(make_pair(W[i] + T[0], 0));  // 这里一定要把小的W数组放进队列，不然会TLE
  G.clear();
  while (G.size() < k && q.size()) {
    pair<int, int> cur = q.top();
    q.pop(), G.push_back(cur.first);  
    if (cur.second + 1 < T.size()) {
      int i = cur.second;
      q.push(make_pair(cur.first - T[i] + T[i + 1] , i + 1));
    }
  }
  T = G;
}

void dfs(int x, int pre) {
  vis[x] = 1;
  int same = 0;
  for (auto [v, val, i] : e[x]) {
    if (used[i]) continue;
    used[i] = true;
    if (!vis[v]) {
      stk[++top] = make_pair(x, val);
      dfs(v, x);
      --top;
    } else {
      W.clear(), W.push_back(val);
      int start = x, cur = top;
      while (start != v && cur > 0)
        W.push_back(stk[cur].second), start = stk[cur].first, cur--;
      merge();
    }
  }
}

int main() {
  ios_fast;
  while (cin >> n >> m) {
    e.assign(n + 1, {});
    W.clear(), T.clear();
    unsigned mst = 0;
    for (int i = 1; i <= n; i++) vis[i] = false;
    for (int i = 1, x, y, z; i <= m; i++) {
      cin >> x >> y >> z, used[i] = false;
      e[x].push_back(Edge{y, z, i});
      e[y].push_back(Edge{x, z, i});
      mst += z;
    }
    cin >> k;
    for (int i = 1; i <= n; i++)
      if (!vis[i]) top = 0, dfs(i, 0);
    unsigned ans = 0;
    if (T.empty()) ans = mst;
    for (unsigned i = 0; i < k && i < T.size(); i++)
      ans += (i + 1) * ((unsigned)mst - T[i]);
    cout << "Case #" << ++Case << ": " << ans << '\n';
  }
}

 

462：4436. 平衡一棵树 - AcWing题库【树上问题】-难题

 

 

463：ARC-A - Many Formulae (atcoder.jp)【组合数学 + 思维 + DP】

题意：给你一个长度为n的数组a，让你加入n-1个加号+或者减号-。同时保证没有相邻的两个减号出现。请你计算所有合法序列的求值结果之和。

我们需要考虑每个a[i]加了多少次，又减了多少次。

定义dp[i][0]为i个符号，最后为减号的方案数，dp[i][1]为i个符号，最后为加号的方案数。

那么根据乘法原理，a[i]加了dp[i][1]*(dp[n-i-1][0]+dp[n-i-1][1])次；减了dp[i][0]*dp[n-i-1][1]次。积累贡献，得到的就是答案。

 

464：Buy and Resell【贪心 + 思维 + 优先队列】

题意： 有一种商品 有n个城市 城市的这种商品价格为ai  有个人 第i天的时候去i城(总共n天)   只能选择一种操作一次  1.买一个 2,卖一个. 3 什么也不做 一开始他是无限的钱 求它的最大利润  利润最大的情况下的最小交易次数。

感觉是一种比较巧妙的贪心。考虑前i-1天的一个状态，每一天要么什么都没干，要么是买入状态，要么是卖出状态。

第i天我们现在来了一个a[i]，考虑i-1天之中选一天j，满足a[j]<a[i]，使得答案加上a[i]-a[j]。

有这些可能：

① 第j天什么也没干，那么直接ans+=a[i]-a[j]即可，a[j]和a[i]这两天都有了状态，同时操作数+=2。 【 要求a[j]是所有无状态的天里最小的。】

② 第j天属于买入状态，那么必然存在一个k，他们对答案的贡献是:a[k]-a[j]。如果a[i]要和a[j]匹配，那么就会多出一个a[k]，他就变成了未匹配的状态（即无状态）。

③ 第k天属于卖出状态，这种情况和第②种一样。因为他们对答案的贡献都是a[k]-a[j]，不如直接拿a[i]-a[j]，然后多出一个a[k]。

查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using ll = long long;
const int maxn = 2e5 + 7, mod = 1e9 + 7;

#define PII pair<int, int>
int n, a, b;
ll ans, cnt;

void solve() {
  cin >> n;
  ans = cnt = 0;
  ll cur_sum = 0, cur_cnt = 0;
  priority_queue<PII, vector<PII>, greater<PII>> q;
  // PII first是权值，second为1说明它没有被匹配过，为0说明它是匹配的右端点
  for (int i = 1; i <= n; i++) {
    cin >> a, b = 1;
    while (q.size() && q.top().first < a) {
      PII p = q.top();
      q.pop();
      cur_sum += a - p.first;
      cur_cnt += p.second;  // 如果p没有被匹配过，那么就从p买入，现在卖出
      q.push(make_pair(a, 0));
      a = p.first, b = !p.second;
      // 如果他没有被匹配，现在它作为买入被匹配，如果它被匹配，现在它被a替代，所以状态转换
      if (cur_sum > ans || (cur_sum == ans && cnt > cur_cnt))
        ans = cur_sum, cnt = cur_cnt;
    }
    if (b) q.push(make_pair(a, 1));  // 如果a没有被匹配，那么它可以放入优先队列
  }
  cout << ans << " " << 2 * cnt << '\n';  // 买入+卖出 所以要乘2
}

int main() {
  ios_fast;
  int TEST;
  cin >> TEST;
  while (TEST--) solve();
}

 

465:【UR #1】缩进优化 - Problem - Universal Online Judge (uoj.ac)【巧妙暴力 + 取模 + 整除 + 思维 + 最小答案】

题意：给定一个序列a，值域范围为1e6，求一个x，使得\(\sum^n_{i=1}(\lfloor\frac{a_i}{x}\rfloor + a_i\%x)\) 最小。

这个题没有性质，于是就想暴力，但是暴力也不好想。

难点在于没有办法同时枚举 向下取整的整数除法的值 和 取模的值。

当我们枚举X的时候，整数除法存在一些区间是相等的\([0,X-1]、[X,2X-1]、...\)，只要开一个权值桶，这样就解决了整数除法的权值。

但是他们的取模怎么计算呢？貌似他们的取模就是 \(sum[K*X-1] - sum[(K-1)*X-1] - X*(cnt[K*X-1]-cnt[(K-1)*X-1])\)

既然两者都可以求，就解决这道题了。【后记：输入一个a,sum[a]+=a, cnt[a]++;】

 

466：介绍一个刚刚想到的算法：分类讨论优化埃式筛方式的枚举 - 某一类暴力

尽管这个名字有点搞笑，但是感觉还挺妙。

我们知道用埃式筛的枚举方式去枚举，复杂度是调和级数的\(nlnn=n*(\sum\limits_{i\ge 1}\frac{1}{i})\)

对于一些题目，他们的值域达到1e7、1e8、甚至是1e9，你还能用这个方式去枚举吗？不太可能吧。

但是如果题目说，数组的值域很大，但是数组的长度比较短(比如1e5、2e5、5e5之类的，超过1e6就不太好控制了)

那么我们可以选择分类讨论暴力。 - 前提是这么做可以解决我们要求解的问题。

也就是分成两个步骤求贡献。

① 我们选择一个\(D\)，把值域在\([1,D]\)内的数取出来，然后再和剩下\(O(n)\)个数暴力求贡献。这部分复杂度是\(O(D*n)\)的。当\(n=1e5，D选择为100\)时，复杂度也就才\(1e7\)

② 对于值域在\([D+1,1e7]\)范围内的数，我们直接采用埃式筛的方式去枚举（前提是拆分不影响贡献的计算）。这部分复杂度是\(O(1e7*(\sum\limits_{i>D}\frac{1}{i})) ≈ O(\frac{1e7}{D}\sum\limits_{i\ge 1}\frac{1}{i}) = O(1e5*ln1e5)\)

然后就可以开心通过某些题目了。

 

例题1：给你一个长度为\(n=1e5\)的数组\(\{a_i\}\)，值域为\(1e7\)，求\(\sum\limits^n_{i=1}\sum\limits^n_{j=1}(a_i \mod a_j)\)，结果对\(1e9+7\)取模

先求出\(\sum\limits^n_{i=1}\sum\limits^n_{j=1}(a_i \mod a_j)[a_i > a_j]\)部分，然后再计算\(a_i<a_j\)部分，这个部分比较好计算，就是有多少个\(a_j\)大于\(a_i\)

查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)

using ll = long long;
const int N = 1e5 + 7, M = 1e7 + 7, mod = 1e9 + 7;

int n, MX, a[N], DIV = 300;
ll sum[M], ans, cnt[M];

inline int randInt(int l, int r) {
  static mt19937_64 eng(time(0));
  uniform_int_distribution<int> dis(l, r);
  return dis(eng);
}

int main() {
  ios_fast;
  n = 1e5;
	double ST = clock();
  for (int i = 1; i <= n; i++)
    a[i] = randInt(1, 1e7), sum[a[i]] = (sum[a[i]] + a[i]) % mod, cnt[a[i]]++, MX = max(MX, a[i]);
  sort(a + 1, a + 1 + n);
	// 先计算有多少个数严格大于自己
	for (int i = 1, j = 1; i <= n; i = j + 1) {
		while (j + 1 <= n && a[j + 1] == a[i]) j++;
		ans = (ans + 1ll * (j - i + 1) * a[i] % mod * (n - j) % mod) % mod;
	}
  // 先处理值比较小的
  for (int i = 1; i <= DIV; i++) {
    if (!cnt[i]) continue;
    for (int j = 1; j <= n; j++)
      if (a[j] > i) ans += (a[j] % i) * cnt[i];
  }
  // 再处理值比较大的
  for (int i = 1; i <= MX; i++) sum[i] = (sum[i] + sum[i - 1]) % mod, cnt[i] = (cnt[i] + cnt[i - 1]);
  for (int i = DIV + 1; i <= MX; i++) {
    if (cnt[i] == cnt[i - 1]) continue;
    for (int j = i; j <= MX; j += i) {
      ans += (((sum[min(j + i - 1, MX)] - sum[i]) - (cnt[min(j + i - 1, MX)] - cnt[i]) * j) * (cnt[i] - cnt[i - 1]) % mod + mod) % mod;
			ans = (ans % mod + mod) % mod;
		}
  }
	cout << ans << endl;
	double ET = clock();
	cout << (ET - ST) * 1000 / CLOCKS_PER_SEC << endl;
}

 

 

467：P8317 [FOI2021] 幸运区间【分治优化暴力枚举】

题意：给你n个序列，每个序列只有d<=4个数字，让你从中选出连续的几个序列，同时选择k个幸运数字，要求每个序列至少包含一个幸运数字。请你求出最长的连续区间[L,R]，使得[L,R]上的区间都满足上面的条件(即能选出k个幸运数字，每个序列都有幸运数字)。多个满足的，求输出L最小的。

（1）首先考虑最暴力的做法，我们枚举区间的左端点，然后使用搜索的办法加点。即\(d^k\)种不同的方法，每种复杂度都是\(O(n)\)级别的，所以整体复杂度是\(O(n*d^k)\)的。

（2）但是其实我们有很多地方是重复枚举的。而题目又要求是连续区间，所以我们可以考虑分治的做法。。。。（强行分治）

答案有三种来源：

• 来源于[l,mid-1]区间
• 来源于[mid+1,r]区间
• 或者答案区间跨越mid点 - 这种情况我们可以直接暴力往左右两边加点（怎么往两边同时加点呢？这也是个难题，后面考虑怎么实现）

这个仍然是考虑dfs来实现，定义dfs(L,R,set_num)其中L是当前搜索到的左区间，R是搜索到的右区间，set是当前的幸运数字集合。因为长度是\(O(n)\)级别的，每次遇到左侧/右侧能扩展就先扩展，如果不能扩展，那就考虑先把左边添加一个幸运数字。因为dfs深度只有k-1=2层（还有1层在mid那里枚举） 所以实际上很快（希望很快）。

查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using ll = long long;

const int maxn = 1e5 + 7;

int Case, n, d, k, ansL, ansR;
int lim_L, lim_R, cnt, vis[maxn];
vector<vector<int>> a;

void chkans(int l, int r) {
  if (r - l > ansR - ansL || (ansR - ansL == r - l && l < ansL))
    ansL = l, ansR = r;
}

bool chkarr(int id) {
  for (const int& v : a[id])
    if (vis[v]) return true;
  return false;
}

void dfs(int L, int R, bool flag_L, bool flag_R) {
  chkans(L, R);
  if (flag_L) {
    dfs(L - 1, R, (L - 2 >= lim_L && chkarr(L - 2)), flag_R);
  } else if (flag_R) {
    dfs(L, R + 1, flag_L, (R + 2 <= lim_R && chkarr(R + 2)));
  } else if (cnt < k) {
    if (L - 1 >= lim_L) {
      for (const int& v : a[L - 1]) {
        vis[v] = true, cnt++;
        dfs(L - 1, R, (L - 2 >= lim_L && chkarr(L - 2)),
            (R + 1 <= lim_R && chkarr(R + 1)));  // 注意，这里必须重新check
        vis[v] = false, cnt--;
      }
    }
    if (R + 1 <= lim_R) {
      for (const int& v : a[R + 1]) {
        vis[v] = true, cnt++;
        dfs(L, R + 1, (L - 1 >= lim_L && chkarr(L - 1)),
            (R + 2 <= lim_R && chkarr(R + 2)));  // 注意，这里必须重新check
        vis[v] = false, cnt--;
      }
    }
  }
}

void Work(int l, int r) {
  if (l >= r) return chkans(l, r);
  int mid = (l + r) >> 1;
  Work(l, mid - 1), Work(mid + 1, r);
  lim_L = l, lim_R = r;
  for (const int& v : a[mid]) {
    vis[v] = true, cnt++;
    dfs(mid, mid, (mid - 1 >= lim_L && chkarr(mid - 1)),
        (mid + 1 <= lim_R && chkarr(mid + 1)));
    vis[v] = false, cnt--;
  }
}

int main() {
  ios_fast;
  int TEST;
  cin >> TEST;
  while (TEST--) {
    cin >> n >> d >> k;
    cnt = ansL = ansR = 0;
    a.assign(n, vector<int>(d, 0));
    for (auto& b : a)
      for (int& j : b) cin >> j;
    Work(0, n - 1);
    cout << "Case #" << ++Case << ": " << ansL << " " << ansR << '\n';
  }
}

 

 

468：P7789 [COCI2016-2017#6] Sirni【最小生成树 + 连边数量有限 + 优化埃式筛枚举】

这道题虽然n比较小，但是值域V很大。应该可以知道，要用埃式筛的方式去枚举连边，可是值域这么大，怎么保证复杂度呢？

我们发现，枚举的[dx,(d+1)x)区间有很多是空的，我们可以通过剪枝剪掉这些空的区间。唯一的办法是，枚举dx的时候，找到第一个大于dx的\(a_i\)。

但是如果使用二分的话，复杂度仍然很大。反正a数组是静态的，我们不妨用并查集的思想，las[x]指向第一个大于等于x的位置即可。

分析这样做的时间复杂度：如果a数组分布足够均匀，那么对于小于100的数，每一次都会被卡到\(O(n)\)。对于大于100的数，则是\(\frac{1e7}{100}*lnn\)调和级数复杂度再除以100的系数。

得到的边的数量是1e7+1e5*ln1e5级别的，所以不能排序，使用桶排+kruskal可以通过此题。卡空间（

查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)

const int N = 1e5 + 7, M = 1e7 + 7;

int n, MX, a;
int lar[M], fa[M];

vector<pair<int, int>> G[M];

void AddEdge(int x, int y) { 
  if (!x || !y) return ;
  G[min(x % y, y % x)].emplace_back(x, y);  
}

int Find(int x) { 
  return (!fa[x] || fa[x] == x) ? x : fa[x] = Find(fa[x]);
}

int main() {
  ios_fast;
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> a, lar[a] = a, MX = max(MX, a);
  for (int i = MX - 1; i; i--)
    if (!lar[i]) lar[i] = lar[i + 1];
  for (int i = 1; i <= MX; i++) {
    if (lar[i] != i) continue;
    if (lar[i + 1] > i && lar[i + 1] < i + i) AddEdge(i, lar[i + 1]);
    for (int j = i + i; j <= MX; j = (j / i + 1) * i) j = lar[j], AddEdge(j, i);
  }
  long long ans = 0;
  for (int i = 0; i <= MX; i++) {
    for (auto [x, y]: G[i]) {
      int fx = Find(x), fy = Find(y);
      if (fx == fy) continue;
      fa[fx] = fy, ans += i;
    }
  }
  cout << ans << endl;
}

 

469：E. Almost Perfect【动态规划思想 + 递推计数 + 排列的逆？就是置换的逆方向】

首先看到这道题\(p_i=j\)，说明置换i->j有一条边。而\(p^{-1}_j=i\)说明在逆排列中这条边变成j->i。继续考虑\(p_i=j和p^{-1}_i=k\)，说明j和k在置换上是在i两侧的。条件转化为置换上任意距离等于2的节点编号之差小于等于1。

满足上述条件的只有①自环；②二元环；③由两个二元环组成的四元环。

我一直在想怎么用组合数去计算，忘了计算实际可以使用递推完成。。。。。。。。。太久没做DP的计数题了。

先枚举四元环的数量i，那么就是从n-i个位置选出i个位置，再在后面插入一个位置变成2*i相邻的二元环。

考虑把2i个二元环变成i个四元环，就是完全图有多少个完美匹配。但是一个四元环有:(i,j,i+1,j+1)和(i,j+1,i+1,j)两种，所以还要乘上2的幂次。

再考虑剩下n-4i个数组成一些自环和二元环。可以使用dp进行递推。

定义\(F[i]\)为i个数能有多少种方案，\(F[i]=F[i-1]+(i-1)*F[i-2]\)。要么第i个数自环，要么第i个数和剩下i-2个数形成二元环。最后乘起来就是答案。

 

470:P2048 [NOI2010] 超级钢琴【区间前k大 + 主席树/（ST表+堆）】

如果数据范围很小，那么直接求出前缀和之后，\(n^2\)个差值里面取前k大加起来就行。现在优化这个过程。

（1）做法1：使用一个堆维护最大值，然后使用主席树维护[l,r]区间内第k大，每次取出堆顶，就取出k+1大放进堆里面，直到符合要求。

（2）做法2：因为这道题没有询问第k大，而是询问前k大。所以考虑一个ST表求单个区间前K大。对于[L,R]区间，如果最大值出现在x，那么我们取出x之后，第二大就会在[L,x-1],[x+1,R]里面出现。使用堆维护这个过程，每取走一个最大值，就会多出两个区间被分割。那么前k大，空间复杂度为\(O(n+k)\)，时间复杂度为\(O(nlogn+klogn)\)

（3）考虑二分第k大的大小，可惜复杂度是\(O(nlog^2n)\)。

 

471：P4036 [JSOI2008]火星人【平衡树维护字符串hash】

题目要求在字符串中插入、修改字符，同时还有查询两个后缀的LCP。

如果没有插入就直接线段树维护字符串hash就行了。插入的话，也就是splay经典操作而已+区间加法和乘法。

 

 

472：可撤销并查集教程！！！严格鸽！！！

 

 

473：斐波那契字符串系列练习题

例题1：Goodbye2020 G. Song of the Sirens

例题2：G1. Fibonacci Strings

例题3：D. New Year Letter

 

474：P3538 [POI2012]OKR-A Horrible Poem【字符串哈希 + 区间循环节】

定义一个字符串S的循环节P，P重复几次可以得到S字符串。显然P的长度m是S的长度n的一个约数。

对于如果T是S的一个循环节，那么T+T仍然是S的循环节（保证|T+T|<=|S|）

所以说，如果P不是S的最小循环节，那么P除去某一个质因子之后，一定还能得到一个更小的循环节。所以我们先求出n的所有质因子，这个是logn级别的。

然后再拿这些质因子去试除，如果能除掉（除完之后还是循环节），那么直接除掉，如果都不行，那么证明我们的循环节就是最小的。

循环节使用hash进行判断，如果学过KMP等等知识，就知道结论：如果str[l,l+m]==str[r-m,r]的话，n-m是一个循环节。

 

474：P4503 [CTSC2014] 企鹅 QQ【思维 + 字符串Hash】

考虑从1到L枚举每一个位置，求出n个串删掉这个位置之后得到的hash值（注意，删去指的是这个位置的hash值为 0）

但是如果把所有的hash值都存下来，不仅仅空间复杂度会达到1e7，时间复杂度也受不了（排序多一个logn）

因为两个串相似，只会有一个位置不同，所以直接枚举i，然后得到某一个位置都被删去的n个hash值，这个时候直接排序计数，就会常数小很多，空间也是3e4的。这样就可以通过此题了。

 

475：P3426 [POI2005]SZA-Template - 印章【KMP + DP + fail树 + 思维】tag加满了属于是！好题

两个做法，都十分抽象，建议当作模板题。

做法1：

考虑DP，定义f[i]为以i结尾的前缀，所需要的最小印章是多大。预处理令f[i]=i。

如果f[i]能够比i小，显然印章一定是该字符串的border。即f[i]<=nxt[i]。而且这个印章一定可以印出nxt[i]这个border。

如果[i-nxt[i],i]区间内，存在一个j，满足f[j]=f[nxt[i]]，那么就可以令f[i]=f[nxt[i]]。 - 这一步可以使用一个桶实现，十分巧妙。

做法2：貌似更抽象。。。暂时不学了

 

476：P1095 [NOIP2007 普及组] 守望者的逃离【贪心 / DP】

如果作为DP练习题，可以定义f[i][20]表示当前过了i秒，还有20的能量的最远距离。（一开始给的M能量肯定是先用完的，逃命要紧麻）转移就比较裸，枚举停留、慢跑、闪现三种选择就行。

还有一种贪心的做法【BLOG】定义f[i]表示过了i秒跑了多远，贪心地从两种方法中取最大值也是可以地（比较 巧妙）

 

477：CF28C Bath Queue【计数DP + 计算期望】

期望题，仍然考虑期望计算的公式 \(\dfrac{\sum\limits_{i=1}i*cnt_i}{tot}\)，其中i是枚举排队的最长长度。

我想了半天，没有想到应该怎么计算最长长度恰好为i的数量，属于是菜。

然后发现了这么个DP定义，定义\(DP[i][j][k]\)为考虑前i个洗漱间，一共j个人分配进去，最长长度为k，那么我们枚举第i+1个洗漱间，把t个人放进去，那么我们很容易进行转移。最后求出来\(dp[m][n][i]\)就是我们要求的\(cnt_i\)，而tot就是dp值之和。

注意使用long double，不然精度可能不够。【需要提前预处理组合数】

 

478：E. Xenia and Tree【树上问题 ： 分治BFS / 线段树+树链剖分】

注意这道题因为只有蓝染红色，比较简单。

做法1：

这一题树链剖分在线段树上具有单调性，对于线段树上每一个节点，它表示的区间是[l,r]，那么更新的时候，就用dep[x]-2*dep[node[r]]来更新线段树最小值。（肯定是选右端点啊，因为树链剖分完之后，dep是连续的，具备单调性，肯定是右端点比较小） - 而且具备单调性的情况下，可以直接pushup中取min。注意，update的过程还是需要使用区间min的懒标记的。查询的时候，就是树链剖分查询最小值而已。

做法2：

对m个询问分成\(\sqrt{m}\)块，在做第i块的时候，前i-1块的染色已经通过BFS更新了树上每个点的答案。对于第i个块要染上去的红色节点，我们只能暴力计算lca同时计算答案了，使用O1的LCA查询，这道题就可以在\(O(m\sqrt{m})\)的时间复杂度内完成。

复杂度分析：对于每一个染色操作，因为是\(O(\sqrt{m})\)次多源BFS，所以整体复杂度\(O(m\sqrt{m})\)。对于每个询问操作，最多只会枚举\(\sqrt{m}\)个点，所以也是\(O(m\sqrt{m})\)。

 

479：CF343D Water Tree【树上问题：从x到根节点的操作 转化为 x的单点操作】

这道题很多人无脑树剖，导致了一些妙妙解法被刷，但是我觉得出题人应该把树剖卡掉。

这道题的第二个操作：x到根的路径上的节点赋值为0；第一个操作：x的子树赋值为1。而这两个操作一个是树链操作，一个是子树操作，都是经典的操作，可惜这里每个点只有两个状态，所以可以用一些奇怪的技巧干掉树剖的logn。

我看题解区两种做法没有用到树剖：

第一种：

建两棵线段树，第一棵线段树代表x被操作1执行到的时间戳，第二棵代表x被操作2执行到的时间戳，然后查询的时候，查询哪个时间错最大即可。

第二种：

如果一个子树全部都是1，那么x的子树权值之和等于子树大小，否则说明x的状态是0。

不过有一个细节，如果x的状态是0，那么说明x的父节点状态必然也是0，所以在进行操作1的时候，应该先判断x的状态是不是0，及时把状态转移到x的父节点上。【有一种可能，x的子树不全是1，但是操作1之后，变成全是1了，如果此时fa[x]来查询，有可能导致fa[x]的子树也全是1，但是fa[x]的状态命名是0】

 

480：G - Reversible Cards 2【值域之和等于M + 暴力背包】

这个题目的一个最重要的性质就是：\(\sum (a_i+b_i) = M\)

那么我们就有 \(Sc = \sum|b_i-a_i| \le \sum(a_i+b_i) = M\)，所以\(b_i-a_i\)的数量是根号级别的，直接暴力多重背包就行。

原因：\(|b_i-a_i| \le |b_i+a_i| \)

细节：双端队列使用数组时实现常数更小，否则TLE。 - 提交记录

 

481：G. Cut Substrings【字符串DP + 删字符串】

一开始以为是\(O(n^2)\)的DP，结果反而不好想转移。好不容易想到\(dp[i][j]\)表示考虑了前i个t出现的位置，且在s中最后删到第j个字符的情况数以及最优答案，结果发现计数很多重复。

发现这道题它一但删掉一个出现位置，很多出现位置都会受到影响，而且他们不能再次被删去，所以我们应该这样来进行转移：

定义\(f[i]\)表示最后删的出现位置是第 i个的最少操作次数，\(g[i]\)则表示方案数，那么我们i应该转移到谁？

假设转移到一个j，那么i和j之间应该满足所有出现位置都被覆盖，所以用双指针扫一遍做DP转移即可。出题人很有意思，是一道纯正思维题，这样暴力DP\(O(n^2)\)是可以通过的。

 

482：G - Random Student ID【思维题 + 概率 + 期望 + 全排列中分成两类的概率】

我们首先考虑把i固定住，然后求i的排名的期望。期望等于概率乘以权重，考虑剩下n-1个同学中，\(\sum\limits_{j\eq i} P_{i,j} * 1\)，即对概率求和。

我们考虑概率怎么计算，有以下三种情况：

• 如果s[j]是s[i]的一个前缀，那么j的排名一定在i之前，所以概率为1
• 如果s[i]是s[j]的一个前缀，那么j的排名一定在i之后，所以概率为0
• 否则两者一定会在LCP之后区分字典序大小，此时，只跟这两个字母的大小有关，我们发现既然是两个字母瓜分全集，那么概率自然就是1/2

根据这个规则对p数组求一下和就行了，具体实现可以使用Trie。

 

483：E - Chinese Restaurant (Three-Star Version) 【环上左侧距离、右侧距离的分割点 + 单调性 + 双指针思想 + 环上距离等价类】

（1）首先你要会第一道easy版本：C - Chinese Restaurant 

我们考虑对于对于一个i，在右边找到p[j]==i的j，那么对于i来说，他只有在转盘往左转j-i长度，才会有p[i]==i的局面。

我们把所有的 j-i = k 的建一个同余类，表示当转盘左转 k 长度的时候，在同余类中盘的下标和人的下标相等。

因为此时我们转动了k个距离，题目要求的 |p[j]-j| <= 1实际上就是 \(k - 1\le x \le k + 1\) 的这么一个条件，也就是说，当我们转动k长度时，cnt[k-1]+cnt[k]+cnt[k+1]就是答案。 

（2）在上面这道题的基础上，我们来做这道更难的题：

查看代码

const int maxn = 2e5 + 7;
int n, a[maxn];
long long ans, cur_ans;

void update(int l, int r, int v) {
  l = (l % n + n) % n, r = (r % n + n) % n;
  if (l > r) {
    a[l] += v, a[n] -= v;
    a[0] += v, a[r + 1] -= v;
  } else {
    a[l] += v, a[r + 1] -= v;
  }
}

int main() {
  ios_fast;
  cin >> n;
  for (int i = 0, p; i < n; i++) {
    cin >> p;
    cur_ans += min((p - i + n) % n, (i - p + n) % n);
    // p - i 是这个 p[i] 向右移动这么多位才能重叠在一起
    // p 位置左侧n/2个点是 -1
    update(-i + p - n / 2 + 1, -i + p, -1);
    // p 位置右侧n/2个点是 + 1
    update(-i + p + 1, -i + p + n / 2, 1);
  }
  ans = cur_ans;
  for (int i = 1; i < n; i++) {  // 把环p向右移动i位 
    a[i] += a[i - 1], cur_ans += a[i];  // 转移圆环的同时顺便维护前缀和
    ans = min(ans, cur_ans);
  }
  cout << ans << endl;
}

 

484：F - Exactly K Steps【树的直径 / 点分治】

对于一棵树，每次询问一个（x,k）求离x的距离为k的点。如果没有输出-1。

我们知道对于树上的任意一个点，距离他最远的点v一定是直径的端点之一。

那么我们询问一个点的距离为k的点，我们直接贪心地在以直径端点为根地树上找就行了。假设直径端点为r1，r2。

我们分别建立两棵有根树，如果两棵有根树都没有距离x为k的祖先节点，那么答案就是-1。 - 这个过程我们使用倍增求第k祖先就行。

或者考虑使用点分治。 - 下面是点分治代码

查看代码

const int maxn = 4e5 + 11;

struct Query {
  int k, i;
};

int n, q, vis[maxn], sz[maxn];
int root, mx_son[maxn];
vector<vector<int>> e;
vector<vector<Query>> qr;
int ans[maxn];

void find_root(int x, int pre, int tot) {  // 注意，这个tot一定不能是引用
  mx_son[x] = 0, sz[x] = 1;
  for (const int& v : e[x]) {
    if (v == pre || vis[v]) continue;
    find_root(v, x, tot);
    sz[x] += sz[v];
    mx_son[x] = max(mx_son[x], sz[v]);
  }
  // 最大儿子的大小严格小于n/2的是重心，这样的重心最多两个
  mx_son[x] = max(mx_son[x], tot - sz[x]);
  if (root == -1 || mx_son[x] < mx_son[root]) root = x;
}

int dep[maxn], mx_dep, bel[maxn], nd[maxn], ndcnt;
vector<pair<int, int>> buc[maxn];

void dfs(int x, int pre, int bel_id) {
  sz[x] = 1;  // 这里重新计算size，为了下一次求重心做准备
  dep[x] = dep[pre] + 1, nd[++ndcnt] = x;
  mx_dep = max(mx_dep, dep[x]), bel[x] = bel_id;
  if (buc[dep[x]].empty() || (buc[dep[x]].size() < 2 && buc[dep[x]][0].first != bel_id)) 
    buc[dep[x]].push_back(make_pair(bel_id, x));
  for (const int & v : e[x]) 
    if (!vis[v] && v != pre) dfs(v, x, bel_id), sz[x] += sz[v];
}

void Work(int x, int tot_sz) {
  // if (tot_sz <= 1) return vis[x] = true, void();  
  // 别忘了给vis赋值，实际上这一题，不要if return 也不影响答案
  root = -1, find_root(x, 0, tot_sz), vis[root] = true;
  for (int i = 0; i <= mx_dep; i++) buc[i].clear();
  int bel_id = 0;
  nd[ndcnt = 1] = root, bel[root] = dep[root] = 0, mx_dep = 0; 
  // bel、dep、mxdep 都注意初始化，否则 wa9
  buc[0].push_back(make_pair(0, root));
  for (const int& v : e[root]) 
    if (!vis[v]) dfs(v, root, ++bel_id);  // 这里dfs也要判断 vis
  for (int i = 1; i <= ndcnt; i++) {
    int x = nd[i];
    for (auto [k, i]: qr[x]) {
      if (k < dep[x]) continue;
      k -= dep[x];
      for (const auto& [id, v] : buc[k]) 
        if (id != bel[x]) ans[i] = v;
    }
  }
  x = root;  // 这里记得赋值x=root，因为递归之后root会变化
  for (const int & v : e[x]) 
    if (!vis[v]) Work(v, sz[v]);  // 这里必须判断 vis
}

int main() {
  ios_fast;
  cin >> n;
  e.assign(n + 1, {});
  qr.assign(n + 1, {});
  for (int i = 1, x, y; i < n; i++) {
    cin >> x >> y;
    e[x].push_back(y), e[y].push_back(x);
  }
  cin >> q;
  fill(ans, ans + maxn + 1, -1);
  for (int i = 1, u, k; i <= q; i++) {
    cin >> u >> k;
    qr[u].push_back(Query{k, i});  // 把询问离线下来
  }
  Work(1, n);
  for (int i = 1; i <= q; i++) cout << ans[i] << "\n";
}

 

485：4. 寻找两个正序数组的中位数 - 力扣【思维】

这个题其实可以扩展成：两个有序数组合并之后的第k小。

其实就是不断删掉k/2个数的过程，直到前k-1小的数都被删掉，那么两个数组前面最小的数，就是第k小的数。

如果一个数组的长度比k/2小 ，那么这个数组就拿最后一个数和另一个数组的第k-len个数进行比较，删掉小的那一侧。

最后我们直到k=1结束循环，并且返回两个数组剩下的最小的元素。

 

486：F - Main Street【基础题  + 分类讨论】

很容易想到把一个点转移到它4个方向的大街上。但是后面就需要分类讨论了。

（1）当 sx 和 ex 处于 同一个块时（即sx/B==ex/B）, 别忘了判断(sy%B==0 && ey % B == 0)

• 第一种情况：sy!=ey 这个时候，答案是 abs(sy-ey) + [sx和ex到主干道的最小距离]
• 第二种情况：sy==ey的时候，因为 两个点在同一列不同行，直接abs(sx-ex)就是答案

（2）当 sy 和 ey 处于 同一个块时（即sy/B==ey/B）, 别忘了判断(sx%B==0 && ex % B == 0)

• 第一种情况：sx!=ex 这个时候，答案是 abs(sx-ex) + [sy和ey到主干道的最小距离]
• 第二种情况：sx==ex的时候，因为 两个点在同一行不同列，直接abs(sy-ey)就是答案

（3）除了上面两种情况， 直接计算曼哈顿距离即可。

我就是因为忘了两个点在同一列不同行/同一行不同列的情况，wa到怀疑人生。以后吸取教训了。

 

487：G - Replace【区间DP + 编译原理：字符推导/产生式推导 + 状态难设计 + 两个DP数组相互辅助转移】

不会做这题，参考题解。

。。。。。。谁TM会谁做。。。。

 

 

 

488：F - Find 4-cycle【鸽巢原理 + 二分图四元环】

这道题和2022年某场牛客多校的技巧一摸一样。

我们枚举S中的点，然后再 \(O(T^2)\)枚举它能到达的节点。记录为\(buc[x][y]\)。

如果一个\(buc[x][y]=0\)，那么就让\(buc[x][y]=s_i\)，否则我们就找到了一个四元环。

这么做的话，找到一个答案就可以直接退出，否则会影响时间复杂度。

因为每个buc都会至多被赋值1次，如果被第二次赋值，那么说明找到了答案。所以复杂度是T平方级别的。

 

489：CF1083C Max Mex【线段树维护树链的连通性 + 二分思想转换为前缀问题】【扶苏大人的题解】

这道题显然是满足单调性的，即如果[0,a]之间的数能在同一条树链上，那么[0,a-1]的数一定可以在同一条树链上。

如果不考虑修改，那么我们就是从小到大for一遍，找到一个最大的k，使得[0,k]都能在一条树链上。那么答案就是k+1。

关键在于怎么合并树链，注意这道题，合并的两条树链不是相离的，有可能出现0-2-1这种先连接0-1再加2进去的情况。

• 所以对于两条链，如果合并之后还是一条链，我们可以使用这种办法：
  • 从4个旧端点中枚举2个端点(x,y)，如果剩下的两个点(u,v)都在(x,y)这条链上，那么它们就能合并成一条链；且这条链的两个新端点就是(x,y)。
• 怎么判断u是不是在(x,y)这条链上呢？
  • 假设lca(x,y)=t，u在链上等价于：\((lca(u,x)==u \| lca(u,y)==u) \&\& (lca(t, x) == t)\) 

但是如果考虑带修改，就需要上线段树了。

考虑使用线段树维护前缀问题，然后在线段树上二分可以找到答案。但是求LCA需要使用欧拉序优化成O(1)。

 

490：CF213E Two Permutations【线段树维护相对大小  + 线段树维护Hash】

主要是这一题，它要求的是子序列，这就导致了差分是不可能的，同样，hash也只能对连续的区间来做，所以问题转化是必然的。

首先看到两个序列a，b都是排列，那么我们可以做出第一步的问题转换。

令ca[a[i]] = i, cb[b[i]] = i。然后我们可以双指针去扫cb[1,n]/cb[2,n+1]/cb[3,n+3]....一系列的区间。

只要它们的相对大小和ca数组一样就行了。但是我们怎么判断相对大小关系是否一样呢？还要求在滑动窗口的同时完成维护。

考虑ca数组的hash值： \(hash = ca_1 + ca_2 * pw + .... + ca_n * pw^{n-1}\)

考虑cb数组长度为n的区间的hash值：  \( rank[cb_{t}] * pw^{t-1} + rank[cb_{t+1}] * pw^t + rank[cb_{t+2}] * pw^{t-1} + .... \)

可以看到\(pw\)的幂次相差了 \(pw^{t-1}\)。

所以求出cb的hash值之后，让ca的hash值乘上\(pw^{t-1}\)就可以比较了。

但是怎么求rank呢这个可以使用线段树维护size实现，在pushup的时候给右儿子重新计算一下就行了，大概类似：

• \(hash[x] = hash[ls] + size[ls] * sum[rs] + hash[rs]\)
• \(sum[x] = sum[ls] + sum[rs]\) - \(sum\)是\(pw^t\)的和

 

491：2022 Hubei 省赛-H题Hamster and Multiplication【数位DP + 数位相乘】【提交链接】

一开始看成了数位相加，想得简单了（x

（1）反思1：我再强调一遍，数位dp的定义是这样的捏：定义dp[len][mul][limit][lead]为当前剩余len个数位，前n-len个数位乘积为mul，大小限制为limit，前导零状态为lead的答案。

  之前做的数位DP题都是对数字计数，导致我忘了数位DP其实本质上还是一个无有向无环图路径计数问题（x

  它不仅仅能作为路径计数问题，还能作为路径求贡献的一种方法呀。

  当len=0的时候，我们根据mul算出答案就行了，然后就像有向无环图DP的时候，做一下记忆化，加快一下速度。其本质是这个样子的呀，虽然有很多种定义状态的方法，但是把前n-len位的状态记录下来也是一种状态设计手段，而且十分常见捏。

（2）启发2：虽然这道题的数据范围n=1e18，但是实际上，数位乘的数量是很少的。你看看9*9乘法表，虽然是81的规模，但是去重之后只有36个数字。做了一下测试，1e9大概也只有3000多个数，1e18大概是9e4个数左右。

  所以我们使用一个map代替dp数组来做记忆化搜索，就可以解决这道题。

  如果你还是不知道该怎么搜，你可能还是没有理解我的"反思1"。

 

 

492：G - Access Counter【使用DP来求解一些概率问题 + 矩阵快速幂优化DP】【提交记录】

说实话，做这道题的时候是好运的，我没有想到太离谱的解法上去。

首先我观察到这是一个循环节，那么问题必然跟循环节的概率有关。

然后我发现我会求解n=1的情况，定义\(a[i]\)为第一个access在第i点出现的概率，这是一个等比数列求和，可以计算的捏。

既然n=1我会求解，我不妨单步单步地思考。因为我上面已经计算出n=1地情况，剩下m-1步就可以继续转移了。没错，这种单步转移很适合使用dp+矩阵快速幂优化，然后我们就解决这道题了。

关键是想到单步转移+DP方程+矩阵快速幂。 - 嘶，一开始遇到概率题还想着放弃，没想到睡一下又会了（x

 

493：2021CCPC广州 K. Magus Night【莫比乌斯反演 + 容斥 + 暴力】

一开始还没想明白\(m^n\)有什么用（x，原来是我读题读歪了，它不合法的贡献是0，也被计入总数了，所以乘上\(m^n\)之后，分母就不见了，说是求期望，实际上是求所有可能的价值之和。

容易想到容斥解决。但是不能拆得太细。

\(ans = (\dfrac{(1 + m) * m}{2})^n - ans(gcd>q) - ans(gcd\le q \and lcm < p)\)

不需要拆成4个条件，拆成3个条件也是可以容斥的(x - 但是这道题最难的地方是最后面的暴力。

\(ans(gcd>q)\)可以使用容斥（或者更贴切地应该叫在倍数和基础上做容斥？），调和级数的时间复杂度完成。

考虑\(ans(gcd\le q \and lcm < p)\)。- 这个搜了一圈题解，发现大家都是暴力求解的，唉，是我太笨了，一直在推式子，推捏嘛。

最后时间复杂度:\(O(n(logn+logp))\)， \(logp\)是质因子数数量，比较小的。

这个暴力也有点巧妙，可以说是这么一个板子：\(n\)个数，每个数可以从\([1,m]\)之间选，求最后选出的序列的\(lcm=i \and gcd=j\)的所有价值之和。一个序列的价值: \(\prod v_i\).

• 先来做质因数分解，得到\(i=p_1^{r_1}\cdots p_k^{r_k}\)和\(j=p_1^{l_1}\cdots p_k^{l_k}\)。
• 单独考虑每个质因子的贡献。  - 这一步的理解十分重要，为什么可以单独考虑呢？
  • \(\prod v_i\)肯定是每个质因子的幂次相乘的！！！ 单独考虑某个质因子的时候， 求出\(p_i^{t_i}\)就可以了。
  • 但是对于单个质因子来说，\(p_i^{t_i}\)怎么求呢？ - 容斥！
  • 因为对于\(p_i\)来说，序列中每个数的\(p_i\)的指数在\([l_i,r_i]\)区间里面。令\(P(l,r)=(p_i^{l_i} + p_i^{l_i+1} + \cdots + p_i^{r_i})\)， 那么容斥答案就是 \(P^n(l,r)-P^n(l+1,r)-P^n(l,r-1)+P^n(l+1,r-1)\)
• 最后再乘起来就是\(lcm=i \and gcd=j\)的合法贡献。

计算方法：

• 对于质因子，可以先预处理最小质因子实现\(O(logp)\)时间复杂度求出所有质因子，然后\(P^n(l,r)\)只能用快速幂来算，所以计算一个\(Ans(lcm=i \and gcd = j)\)的复杂度为\(O(logplogn)\)
• 但是当\(gcd=1\)时，我们可以对\([1, 2 * maxn]\)预处理出\(pw[i]=i^n\)，然后等比数列求和之后直接查询n次幂就行了。所以这道题时间复杂度是\(O(n(logn+logp))\)

 

494：D. Journey to Un'Goro【构造 + 思维 + 搜索】 - 2020年沈阳站

一开始我认为最大一定是全1串，答案是(n+(n-2)+(n-4)+...)，但是这么想是推不出下一步的，因为没有扩展性。

考虑字符r的前缀和数组，中间有奇数个r，一定是存在 p[i]-p[j] 是一个奇数。同时p[i]、p[j]一奇一偶。

假设前缀和数组p有x个奇数，y个偶数，那么答案就是x*y。最优情况下肯定是x和y比较接近的。

所以不妨假设\(x=\lceil\dfrac{n+1}{2}\rceil\)和\(y=\lfloor\dfrac{n+1}{2}\rfloor\)。 - 因为前缀和数组一共有n+1个数，且第一个数一定是0。

我们在搜索的过程中，保持x和y都小于等于\(\lceil\dfrac{n+1}{2}\rceil\)就行了，然后这么搜索的话其实是很快的。具体代码参考别人的：D. Journey to Un‘Goro （思维+搜索）

细节：多加括号：  ((n+2)/2) * ((n+1)/2)

 

495：H. Holy Sequence【2020ICPC秦皇岛】 - DP预处理 + 统计答案 【参考题解】

直接定义DP方程求解这个问题，得到一个\(O(n^4)\)的做法，想了一下优化方法，貌似不太可以做。（至少要维护 (cnt，X) 表示 \(X^2\)出现了cnt次才能 求出贡献）

也许这个问题并不是纯DP问题，它需要经过一些统计技巧、建模技巧来求解。

这么去想的话，我们把重心放在统计上。我们考虑数字i出现了多少次，在所有合法的序列中，我们找到第一个出现i的位置j，j后面每一个的i就可以通过组合数枚举出现的位置（因为题目求的是平方，所以最多只需要使用组合数枚举两个出现的位置）。 - 可能是一个比较经典的技巧？

上面的原理是因为：\(X^2 = 2*C(X,2) + C(X, 1)\)吧大概。然后就像很多题解说的一样，枚举4种情况求答案就行了。

这个后缀DP也是挺难理解的，定义\(g[i][j]\)表示：以\(j\)开头，长度为i的好序列的数量。它的转移方程是这样的：\(g[i][j]=g[i-1][j]*j+g[i][j+1]\)。因为是倒着DP，我们只有当前头是j的这么一个信息，所以要么在数列一开始加上一个j-1，要么在数列第2位加上1~j这j个数，DP的转移方程就这么理解就行了。这个转移是完全的，因为当我们使用这个DP状态的时候，我们没有保留数列第2位的大小，所以只能把一个新的数插入到数列头或者数列第2位了。

upd: emmm大概就是预处理\(f[i][j]\)表示长度为i的末尾max是j的holy序列有多少个，\(g[i][j]\)表示长度为i以j开头的holy序列有多少个。然后求贡献的时候就是计算二元组的数量。我们枚举数字\(num\)第一次出现的位置\(pos\)，然后再使用组合数把另一个\(num\)插入到\(pos\)后面。这样就完成了计数（

查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)

const int maxn = 3e3 + 3;
int n, m, f[maxn][maxn], g[maxn][maxn], ans[maxn];

int main() {
  ios_fast;
  int T;
  cin >> T;
  for (int kase = 1; kase <= T; kase++) {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
      ans[i] = 0;
      fill(f[i], f[i] + n + 1, 0);
      fill(g[i], g[i] + n + 1, 0);
    }
    f[0][0] = 1;
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= i; j++) {
        f[i][j] = (1ll * f[i - 1][j] * j % m + f[i - 1][j - 1]) % m;
      }
    }
    for (int i = 1; i <= n; i++) g[1][i] = 1;
    for (int i = 2; i <= n; i++) {
      for (int j = 1; j <= n; j++) {
        g[i][j] = (1ll * g[i - 1][j] * j + g[i - 1][j + 1]) % m;
      }
    }
    for (int i = 1; i <= n; i++) {    // num
      for (int j = 1; j <= n; j++) {  // pos
        ans[i] = (ans[i] + 1ll * f[j - 1][i - 1] * g[n - j + 1][i]) % m;
        ans[i] = (ans[i] + 3ll * (n - j) * f[j - 1][i - 1] % m * g[n - j][i]) % m;
        if (j <= n - 1) ans[i] = (ans[i] + 1ll * (n - j) * (n - j - 1) *  f[j - 1][i - 1] % m * g[n - j - 1][i]) % m;
      }
    }
    cout << "Case #" << kase << ": \n";
    for (int i = 1; i <= n; i++) cout << ans[i] << (" \n"[i == n]);
  }
}

 

496：G - Random Walk to Millionaire 【期望转化成为概率DP】【提交记录】

一般我们求期望题的时候，要么通过公式推导+化简求解，要么通过多加一维状态表示权重的概率DP。

可惜这道题目的求和贡献是平方级别的，实在是太大了，无法通过状态维护权重，而且貌似也没什么公式推导。

这道题最牛的地方在于，他把一条路径上的平方贡献转化为了二元组计数。然后还用简单的[0/1][0/1]的DP状态来作为等价类统计求和！

思路如下：

Part - 1 化简问题

回到原问题，题目求的是： 所有从1开始的长度为k的路径path的权重 * 该路径的概率。即： \( \sum\limits_{path} W(path) * P(path)\)。

根据题意：一条路径的权重 = 路径上所有颜色为1的节点的权重之和。而题目求的\(X^2\)我们可以看成颜色为0的节点组成的二元组(x,y)。所以一个c=1的节点U的权重是以U节点为前缀的路径上二元组的数量\(W(u)\)。

所以问题变成：\(\sum\limits_{path} (\sum_{u∈path}W(u)) * P(path)\)。

但是以u为终止节点的前缀路径有很多条，所以u作为概率树图上面的父节点，求和之后，就只是这一段前缀的概率了。

所以公式变成：\(\sum\limits_{w} W(u) * P(w) \) 其中\(w\)是长度不超过k，以u作为终止节点的前缀路径。其中\(W(u)\)是路径\(w\)上二元组\((x,y)\)的数量。二元组来作为DP的状态就好多了。

Part - 2 DP求解

定义\(dp[i][j][a][b]\)表示路径长度为i，当前末尾节点是j，[0/1][0/1]代表二元组(·，·)/(·, y)/(x,·)/(x,y)。因为我们不需要记录二元组上面具体是那个点，只需要记录一个占位符就行了。然后DP的过程就是模拟路径上x节点是否更新二元组就行了吧（x

无法用拙略的言语表述这个巧妙地算法，希望能记住。

 

497：G - Infinite Knapsack【凸包、几何意义、问题转化、求极限】

极限允许无限大，所以可以看成一些小数在比例中出现。

 

 

 

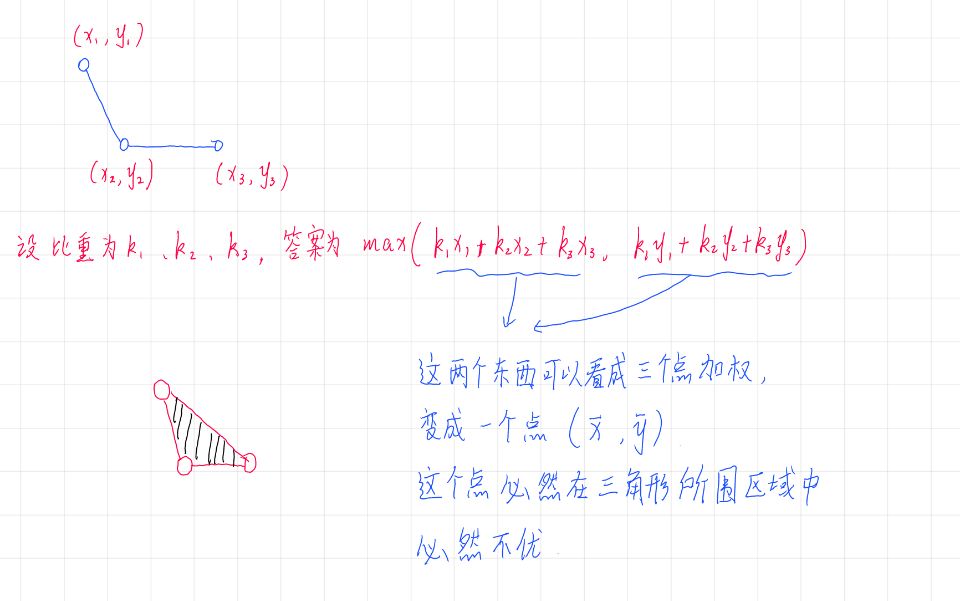
498：C. Complementary XOR【思维 + 构造 + 结论 】

这道题不会写，去看了题解。

启发：一般来说，让你通过某种操作把一个序列变成0，那么可以反其道而行，尝试把一个全0序列变成原序列（只要操作具有逆操作 ）。

从一个全0序列的角度进行思考，我们每一次操作完之后，a序列要么和b序列一样，要么和b序列相反。所以这就是这个 操作具备的特性。

如果不满足这两个条件，就说明无解。否则，我们存在一种构造方法。

先把a序列的每一个位置都变成0，这个可以通过[i,i]操作实现，然后b序列要么全0，要么全1。

如果是全0就不需要再动了，否则可以参考题目样例的操作，再多做3次操作就可以完成转换了。。。。

 

499：E. Bracket Cost【思维 + 括号序列 + 结论】

一开始读错了题，把一种操作看成了整个串shift，但是题目允许子串进行shift (x - 参考了两个不同的做法

（1）做法一【官方题解】【提交代码】

  对于\(\max(sum[L-1],sum[R])-\min\limits_{L-1\le i\le R}\{sum[i]\}\) ，我们拆成两个部分计算，先算最大值的贡献，再算最小值的贡献。

（2）做法二【民间版本】

启发：对于括号序列的区间问题，往往可以从前缀和入手。定义左括号为\(+1\)，右括号为\(-1\)，求出前缀和之后，对于\([L,R]\)区间:

• 它的未匹配的左括号的数量等于\(sum[R]-\min\limits_{L-1\le i\le R}\{sum[i]\}\) - 注意是从\(L-1\)开始
• 它的未匹配的右括号的数量等于\(sum[L-1]-\min\limits_{L-1\le i\le R}\{sum[i]\}\) 

 

 

500：C. Zero-Sum Prefixes

这道题有倒序贪心和直接暴力DP的两种方法：

（1）倒序贪心法：

（2）暴力DP法：