DP练习题
此文为笔记,用于自我反思。
学好DP很难捏,有些DP里面嵌套了数学、有时候又需要使用数据结构维护,有时候需要用到图论的相关知识。好难啊。
决定了,我要存下比较模板的DP题,记住他,理解他。
一、数据结构维护DP
1. div1-D Serious Business 【补题记录】
题意:一个矩阵有3行,n列,每个格子有收益:\(a_{i,j}\)可以小于0,要求你从(1,1)走到(3,n),但是一开始row[2]是被封锁的,你需要花钱来解锁一些线段。你可以花\(k_i\)元来解锁\([l_i, r_i]\),让你最大化你得到的收益.
解析
首先需要转换问题为DP模型。此题的难点在于后面如何转移DP。
预处理出3行的前缀和,那么我们选择\((l,r)\)的答案就是:\(sum(0, 1, l)+sum(1, l, r)+sum(2, r, n)\)
把变量中的l、r拆开,得到:\(F[l]=s[0][l]-s[1][l-1]\)、\(G[i]=sum(2, r, n)+s[1][r]\),那么答案就是:\(F[l]+G[r]+cost(l,r)\),其中\(cost(l,r)\)是选择解封的最小花费。
难点就在怎么计算cost函数,因为它即涉及变量l,又涉及变量r。或者说难点在于对于每个i:[1,n],求出它的决策点(当时我就是这样想的,就G了。此题根本不是问求每个i的决策点,而是求全局最优解)。
正解:考虑只解封\([l,r]\),那么答案就是:\(max(MAX\_F[l,mid]+MAX\_G[mid+1,r],ans[l,mid],ans[mid+1,r])\)。
好,一个块的答案我们解决了。
那么两个块呢?假设为:\([l_1,r_1]、[l_2,r_2] 且 l_2<r_1\),即两者相交。
那么\(ans=max(ans[l_1,r_1],ans[l_2,r_2], MAX\_F[l_1,r_1]-w_1+MAX\_G[r_1+1,r_2]w_2)\)
很理所当然地想到了吧,那么三个怎么办?四个怎么办?
我们从左往右做DP,当求出一个块\([l,r]\)的答案时,顺便拿\(MAX\_F[l,r]-w\)更新\(r_1\)处的权值,这部分用线段树处理。嗯,已经语无伦次了。
2. Skyline Photo【单调栈 + 思维 / 单调栈最大值】【补题记录】
题意:n个二元组(h[i],w[i]),w可以小于0,让你把序列分段,每段的权值是段内最小h的w值,使得每段权值之和最大。
解析
(1)巨佬的BLOG
(2)想一个朴素DP:\( dp[i] = max(dp[j - 1]+value(j, i)\),但是这样做是\(O(n^2)\)的,G了。
(3)考虑优化这个DP,决策单调性、斜率优化在这里都不管用拉!value函数又不满足四边形不等式,G了。
考虑value的来源吧,如果我们根据height维护一个单调递增的单调栈stk,有:\(h[stk[i-1]]<h[stk[i]];(1\le i<top)\)。对于一个 \(j∈[stk[k-1]+1, stk[k]],value(j,i)=weight[stk[k]]\)。
也就是说,我们可以维护\([stk[k-1]+1,stk[k]]\)区间内的最大值\(max(dp[t-1]+w[stk[k]]),t∈[stk[k-1]+1,stk[k]]\),从而大大减少枚举时间。
这样我们维护的stack就是一个二元组\((id, mxval\_of\_[stk_{k-1}+1,stk[k]])\)。
每次转移的时候枚举stack里面的最大值即可。
又由于栈最大值可以\(O(1)\)维护,此题复杂度降到\(O(n)\)。
3. 7154-Slayers Come 杭电多校【线段树维护DP + 计数DP】
解析
这道题难的地方是把一个看似不像DP计数的问题转换成DP计数。
定义: \(DP[i][j]\) 表示考虑前i个技能,[1:j]区间内都被覆盖1次, 且最右能且只能覆盖到j的总数。
那么对于技能i,它能覆盖:\([l_i,r_i]\)区间,显然有如下转移:
对于 \(j>r_i\):\(dp[i][j] *= 2 \) 因为本来就覆盖了,这个技能就可有可无了。
对于\(j = r_i\): \(dp[i][r_i] = \sum^{r_i}_{k=l_i-1} dp[i-1][k]\)
对于 \(j<r_i\):不需要转移,\(dp[i][j] = dp[i-1][j]\)
我们定义j是所有区间最右覆盖到j的种数,是为了避免重复计数。 - 为计数的过程加以顺序,从而保证了没有重复。
也正是因为我们对j的定义,所有覆盖区间我们要对他们进行排序:左端点小的排在前面,左端点小的,再根据右端点排序(右端点升降序都是OK的)
upd: 发现根据右端点排序会WA,只能让左端点从小到大排序。不太懂应该怎么理解,直观感受就是,一个区间\([l_i,r_i]\)转移影响的范围是:\([r_i,n]\),那么在计算\([l_i,r_i]\)对\([r_i,n]\)的贡献的时候,应该确保\([1,l_i-1]\)对\([r_i,n]\)的贡献都计算在内了,所以应该按左端点排序。 --- 不是很懂啊,有无懂哥浇一下。
二、状态较难设计转移的DP/转移没写出来
1.2022寒假训练 F.Fence Job
题意:给你一个数组a,你可以进行任意次操作,每次操作让[l,r]所有数字变成[l,r]区间内的最小值。求能形成多少种不同的数列。
解析
一开始就设计状态为:DP[i][j]为考虑前i位,以颜色j结尾的种数,转移的时候发现无法转移。
看题解发现,状态设计为:DP[i][j]为考虑前i为,以a[j]结尾的数量。
好处在于:j可以是大于i的,只要使用单调栈预处理出每个数字左侧小于他的位置,右侧小于它的位置即可。
转移的话,不需要考虑h[i-1]、h[i]之间的大小关系,只需要保证上一个块的id<=当前块的id即可。【这里我们从小到大枚举j进行保证,并利用前缀和优化】
2. F. Even Harder【思维DP】
题意:n个点,每个点可以跳到:[i+1,i+a[i]]处。让你设置一些点的a[i]=0,要求设置的点尽可能少,使得从1到n的类路径唯一。【难点在于状态的设计,想法就是如果当前最后一个点是i,而且从1到i的路径唯一,那么就必须保证倒数第2个点没有办法走到i,所以必须维护倒数第二个点最远能走到哪,才能维护转移】
解析
定义状态:dp[i][j]为最后一个走到的点是\(i\),走到\(i\)的路径唯一,而且倒数第二个点最远能走到\(j\)的最小花费。
考虑DP算法:
第一层循环,枚举当前最后走到的点\(i\),第二层循环:for j in [ i, i+a[i] ),枚举倒数第二个点走到的最远位置,第三层循环:for k in [j+1, i+a[i]],必须保证\(j<k\),需要枚举下一步要走到哪一个点【即选一个新的点作为最后一点】
那么就会有一个朴素的\(O(n^3)\)算法。【查看链接】
然后使用一个mn数组做一遍前缀最小值可以优化至\(O(n^2)\)。

解析
该题状态设计应该一眼状压。但是要怎么维护这个DP?
维护一个string的前缀和Sum,遇到'('加1,遇到')'减一,同时维护最小前缀和Min。
我们假设dp[state]维护的是已经加入state的string,他们按最好的顺序排好的最大合法前缀。【在这种情况下,如果出现未匹配的右括号,那么该串就是已经不合法了;如果出现了未匹配的左括号,因为是合法的串,所以权值和是唯一的。】
既然权值和唯一,我们考虑加入一个str[i]就好办了,分两种情况:
(1)\(sum[state] >= Min[i]\):这个时候加入第i个串之后,\(state|(1<<i)\)仍然是合法的,这个时候可以转移状态,\(dp[new\_state]=max(dp[new\_state],dp[state]+cnt[i][-Sum[state]]\)【其中cnt[i][x]数组维护的是第i个串前缀和为x、且合法(合法指的是当前前缀和就是最小前缀和,如果不是,意味着出现过失配的‘)’而不合法)的出现次数,使用unordered_map计数。】。(2)\(sum[state]<Min[i]\):此时由于状态不合法,但是还是可以更新答案(因为存在一个前缀和state匹配),直接更新ans即可(具体看代码)。
4. E - A Color Game 【区间DP + 辅助DP计算信息】【提交1】【提交2】
题意:给你一个长度为n的字符串,每次可以选择长度大于等于m的一段删掉,问你最后能不能全部删掉。
解析
比赛的时候基本想得差不多了,但是就是没写出来(退役啦!)。
定义F[l][r]为区间L,R能不能删掉,定义D[l][r]为删得只剩str[l]的时候,最多能有多少个str[l]。
(1)F[l][r]的转移有两种:
1.如果str[l]的数量本来大于等于m,那么F[l][r] = F[l+1][r]
2.如果str[l]数量小于m,那么就是F[l][r]=((cnt[l]+D[l][r])>=m),因为此时str[l]必须依赖[l+1,r]里面的颜色str[l]
(2)D[l][r]的转移如下:
如果F[l+1][r]为真,先赋值ans=cnt[l],否则ans=-inf。
然后枚举区间[l+1,r]内的颜色str[l](假设位置为i), 如果F[l+1][i-1]为真,那么str[l]可以和[i,r]合并,ans=max(ans.cnt[l]+D[i][r])。
当然直接靠D数组DP也是可以通过的。
5.Cyclic Buffer【澳门站 + 思维 + 数据结构优化DP模型】
本题先建有向图,在有向图上DP会超时link。。1e6再也不敢建图了,tm常数巨大(考虑换个DP模型)
这个做法是抄wifiiii的(思路还算清晰)。
在这个做法上,也可以用线段树维护区间最小值来做(思路基本上是一样的)。
考虑二维dp,定义dp[i][j]为buffer的当前已经读到第i个数,且左端点在j,需要的最少步数。
那么转移就是: \(dp[i][j] = \min dp[i-1][t] + dis(j, t)\) 【同时要求以t开头的区间不包含pos[i]】
我们发现,包含pos[i]的状态是不会改变的,而不包含pos[i]的状态是有限的(每个i只会贡献 两个端点一左一右)
所以用一个map维护暴力转移就行。
当然,有个细节需要注意。
根据我们定义的状态和转移条件,t开头的区间不包含pos[i]。
一开始我这么写就G了,没有考虑到跟原来的dp[l]取个min(wa了半天。。。)。
6.删库...【namo每日一题把我难倒了: Trie上DP】
这道题k比较小,直接考虑把k放入状态设计里面。
定义dp[x][k]为在Trie树上的x节点后面剩余k个字符串时,最少删了多少遍。
因为Trie的节点数比较少,虽然是\(O(3e5*k^2)\),但是仍然可以通过。直接DP即可。
7.如意【华工校赛的一题经典且简单的DP + 添加一维消除后效性 + 赊账思想】
题意:给你长度为n=5000的01串,每个位置有一个权值b[i],每次可以选择x、y(x<y)两个位置(可以选择01、10、00、11四种),删去这两个位置,得到权值b[y]-b[x]。让你删去01串里面的所有的1,使得总权值最小。(0可以选择删除使得答案最小)
分析:定义dp[i][j]为考虑前i为,已经把前面j个位置当作x减掉了(提前减掉),得到的最小答案。
对于1来说,它必须被删掉:
dp[i][j] = \(min(dp[i-1][j+1]+b[i], dp[i-1][j-1]-b[i])\)
对于0来说,可以选择不删:
dp[i][j]=\(min(dp[i-1][j], dp[i-1][j+1]+b[i],dp[i-1][j-1]-b[i])\)
感觉这道题还是十分巧妙的。
① 贡献具有绝对值,无法直接计算。 -- 所以从小到大依次加入数组中
② 实际上波浪的总权值之和只有\(O(n^2)\)级别
③ 分类讨论众多。。。。。
④ 状态难以设计 -- 一开始dls讲了个状态压缩的解法,但是复杂度不对啊,所以又讲了个填坑DP的做法,反正就是很秀的。。
什么叫填坑DP啊。是把相似的一块数组分类的情形吗?之前只在一道二叉树DP见过。好难啊。听dls讲课听得一脸懵,下课之后才大致搞懂。
9.E - Warp (atcoder.jp)【思维 + 类比】
题意:你一开始在(0,0),如果当前你在(x,y),下一步你可以到达(x+A,y+B)或者(x+C,y+D)或者(x+E,y+F)。但是地图上有m=1e5障碍,你不能到达这些障碍上面。求你一共能有多少种方案跑完300步。
如果是在二维平面上,下一步只能走到(x+1,y)/(x,y+1)的话,你们肯定能够想到定义dp[n][x][y]表示走了n步,到达x,y的方案数。但是这个dp的理解并不是这么固定的!!!
你完全可以理解为,dp[n][x][y]走了n步,x代表(1,0)选了x次,y代表(0,1)选了y次!!这样我们就能完整表达出这个状态。
同样,这道题也是这么做!不要被这么大的坐标范围给限制!定义dp[n][a][b][c]表示一共走了n步,3种选择分别选了a、b、c次的方案数。
转移就是\(O(3)\)枚举上一步选了哪一个方向。然后c=n-a-b,所以空间优化成\(n^3\)就行了。在转移的过程中,使用一个set存储障碍点,计算出当前的坐标,确保当前坐标不在障碍点上(反正就是暴力转移)。
10.P7961 [NOIP2021] 数列【DP】【题解】
通常这种数据范围,如果是DP,要么就是3维+O(n)的转移,或者4维+O(n)的转移。可惜,俺没有慧根,即使想到了一些DP的状态,可都因为转移困难而不了了之。看完题解之后,发现DP的状态也不是这么死板的,比如说这一道题,转移的时候枚举有多少个\(a_i=j\),这样就可算出对下一位的进位是多少,然后一层一层,转移比较容易。。最后跑到m了,但是还有进位怎么办?那就枚举呗。。(指代码里面的popcount(i)枚举还有多少进位)
定义\(F[i][j][k][p]\)为当前考虑了数组[0~i]之间,j表示已经考虑了j个数,k表示[0~i]之间有多少个1,p表示给下一位的进位是多少。
查看代码
#include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using ll = long long;
const int mod = 998244353;
int n, m, K, v[110], pv[110][40];
int f[110][40][40][40], C[40][40];
void add(int &x, int y) { x += y, (x >= mod && (x -= mod)); }
int count(int x) {
int ret = 0;
while (x) ret += (x & 1), x >>= 1;
return ret;
}
int main() {
//freopen("test_input.txt", "r", stdin);
ios_fast;
cin >> n >> m >> K;
for (int i = 0; i < 33; i++) {
C[i][0] = C[i][i] = 1;
for (int j = 1; j < i; j++) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
}
for (int i = 0; i <= m; i++) {
cin >> v[i];
pv[i][0] = 1;
for (int j = 1; j <= n; j++) pv[i][j] = (1ll * pv[i][j - 1] * v[i]) % mod;
}
f[0][0][0][0] = 1;
for (int i = 0; i <= m; i++)
for (int j = 0; j <= n; j++)
for (int k = 0; k <= i && k <= K; k++) // 注意这里k<=K同时k<=i
for (int p = 0; p <= n / 2; p++) // 到下一位的进位不超过n/2
for (int t = 0; t <= n - j && (p + t) / 2 <= 30; t++)
add(f[i + 1][j + t][k + ((p + t) & 1)][(p + t) >> 1],
((ll)f[i][j][k][p] * C[n - j][t] % mod * pv[i][t]) % mod);
int ans = 0;
for (int i = 0; i <= K; i++) {
for (int j = 0; j <= n / 2; j++) {
int bc = __builtin_popcount(j);
if (bc + i <= K) add(ans, f[m + 1][n][i][j]);
}
}
cout << ans << endl;
}
11.F - Manhattan Cafe【思维 + 对角线前缀和】
题意:给定两个n维的点,求有多少个整点到两个点的曼哈顿距离都不超过D。
一开始以为是曼哈顿转切比雪夫,但是是n维的,没有办法做,就不会了。 - 看了题解发现是DP。
定义\(dp[i][j][k]\)表示考虑前i维,离第一个点距离为j,离第二个点距离为k的点的数量。那么转移的时候,就是枚举第i+1维的位置,范围是[-D,D]。
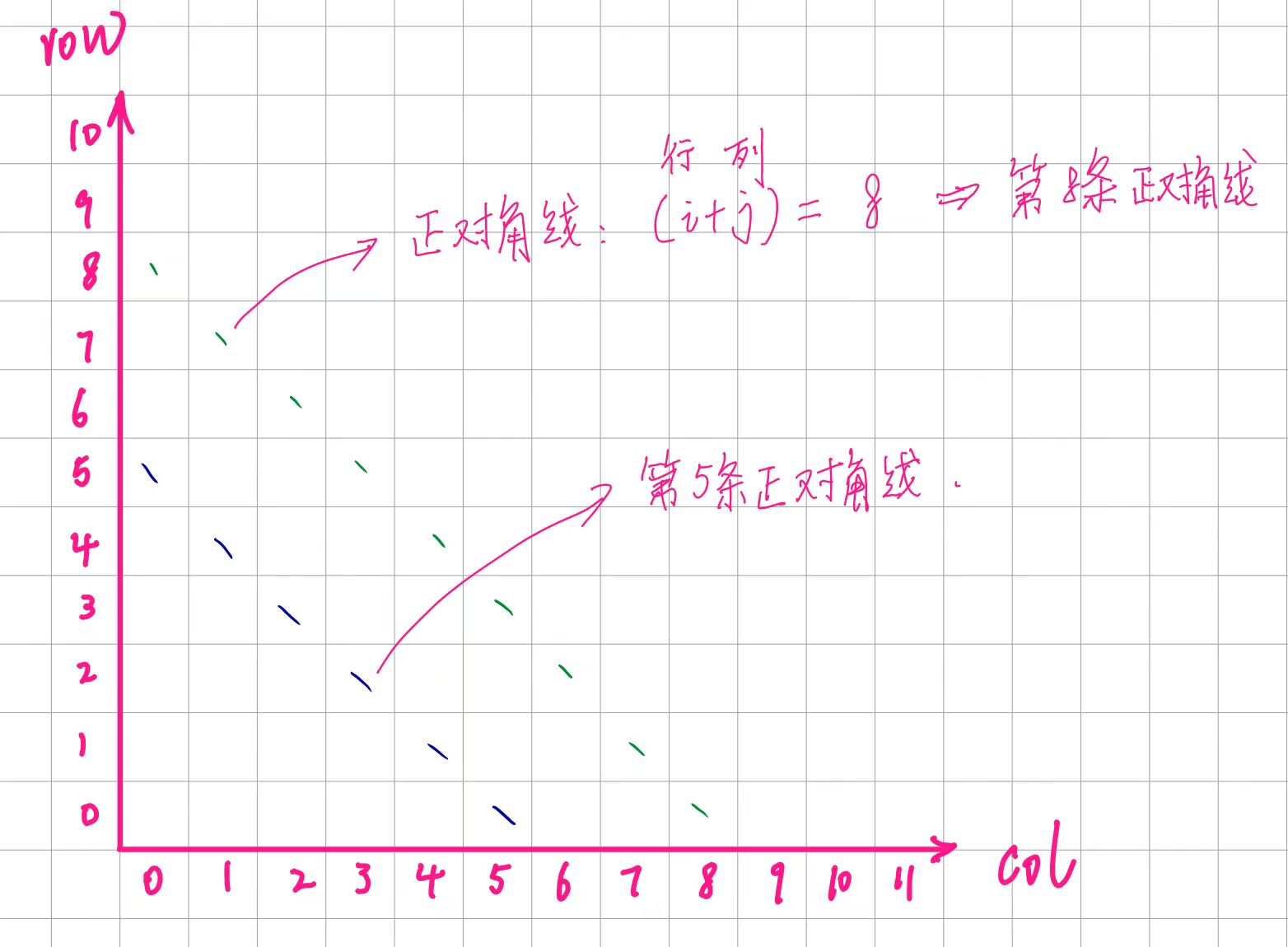
可惜复杂度是\(O(n*D^3)\),无法通过此题。但是我们考虑转移的过程,只有三种类型的 [-∞,p[i]][p[i],q[i]][q[i],∞] 三种转移。分别对应了三条对角线。我们做3次对角线前缀和就行了。
三种转移

【下面来讨论一下对角线前缀和怎么快速写出来】
思路
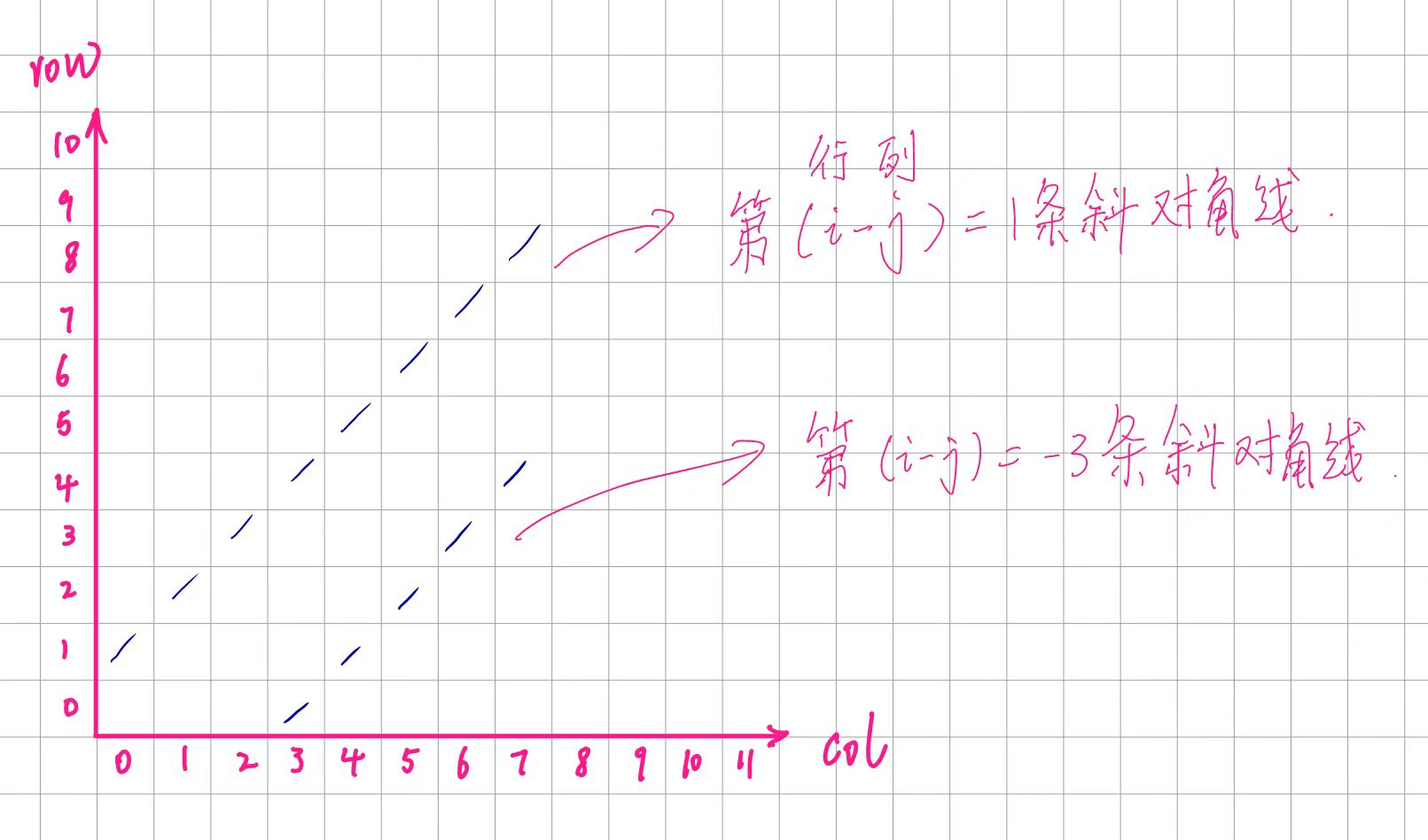
对于正对角线,编号为:(i+j) - 快速前缀和的时候,只需要固定x,那么y就等于ID-X了 ,ID是正对角线的编号
对于斜对角线,编号为:(i-j)
三、发掘特殊性质解决、优化DP/一些优化DP的套路
1. D. Flipping Range 【题解】
解析
看到此题的整个过程:
(1)第一步可能会想到:如果x、y都存在B中,那么等价于x-y也在B中,然后根据裴蜀定理,所有操作等价于gcd(B)。好,这个想法说明你数论还行,但是是不对的,具体看反例:A=[-1 2 2 -1];B=[4,2]。
我们需要发掘其余的性质,但是从gcd这里切入的确就是正解。
(2)上面给出了一个反例:,说明两次操作可能存在包含关系,但是有一个性质,记c[i]为第i个数被操作的次数的奇偶性,奇数次为1、偶数次为0;同时记p为gcd(B)。就是不管怎么操作,都存在c[0]^c[p]^c[2*p]=c[1]^c[p+1]=...=c[p-1]^c[2*p-1]。对p的每个余数做一次DP,然后在异或和为1、异或和为0两者中选择最大答案。
2.G. Subsequences Galore【状压 + 高维前缀和/SOSDP/FWT计算DP】【高维前缀和做法】
解析
不难想到一个容斥,定义H(state)为state中为1的bit的字符串共有的subsequences数量,这个可以通过对每一个字母取min,然后累乘求得,对于每一个state,都要求它的子集和,那么复杂度就是\(O(3^n)\),TLE无法计算。
写出式子来看:\(F[state_x]=\sum_{state_y∈state_x}(-1)^{bitcnt[state_y]}H[state_y]\),那么这个DP就是一个容斥的过程,我们把(-1)这一项放入H函数里面,变成:\(F[state_x]=\sum_{state_y∈state_x}H[state_y]\)。这一步可以使用SOSDP/高维前缀和/FWT维护。【额,菜鸡只会高维前缀和,考虑之后再补充其它两个的做法】。
高维前缀和就是第一层循环枚举第i维,第二层循环枚举其它n-1维,第三层循环对第i维做前缀和(由于二进制状压只有0、1,所以第三维是O(1)的,总复杂度就是\(n*2^n\))。细节就是最后求答案的时候不需要取模、使用dfs计算H数组
3.最长公共递增子序列【模板LIS+LCS】
题意:给两个序列a、b,让你求LCIS。这道题还是典中典的。
同时由于信息都压缩在 F[i]数组里面,滚动一下可以获得更优的空间复杂度。
查看代码
最长公共递增子序列O(n^2)模板——ZOJ2432解题报告- -
ZOJ2432——最长公共递增子序列 WA*2 AC*4
// 时间复杂度 O(n^2), 空间复杂度 O(n^2)
/*
l1为a的大小, l2为b的大小
结果在ans中
f记录路径,DP记录长度
用a对b扫描,逐步最优化
*/
#include<string.h>
#include<stdio.h>
#include<iostream.h>
#define MAXN 500
typedef int elem_t;
int GCIS(int l1, elem_t a[], int l2, elem_t b[], elem_t ans[])
{
int f[MAXN+1][MAXN+1];
int DP[MAXN+1];
int i,j,k,max;
memset(f,0,sizeof(f));
memset(DP,0,sizeof(DP));
for (i=1;i<=l1;i++)
{
k=0;
memcpy(f[i],f[i-1],sizeof(f[0]));
for (j=1;j<=l2;j++)
{
if (b[j-1]<a[i-1] && DP[j]>DP[k]) k=j;
if (b[j-1]==a[i-1] && DP[k]+1>DP[j])
DP[j]=DP[k]+1,f[i][j]=i*(l2+1)+k;
}
}
for(max=0,i=1;i<=l2;i++)
if (DP[i]>DP[max]) max=i;
for(i=l1*l2+l1+max,j=DP[max];j;i=f[i/(l2+1)][i%(l2+1)],j--)
ans[j-1]=b[i%(l2+1)-1];
return DP[max];
}
这题象是LIS和LCS的结合。
能想到的最简单的方法就是对a的每一项和b的每一项进行匹配,当找到一个匹配的
时候,就往回找比它小的一个最长公共子列,如a[i]==b[j],就搜a[0,i-1]*b[0,j
-1]这个矩形里面比a[i]小的最长公共递增子列。简化的代码如下:
for(i=1;i<=l1;i++)
for(j=1;j<=l2;j++)
if (a[i-1]==b[j-1])
{
max=0;
for(i1=1;i1<i;i1++)
for(j1=1;j1<j;j1++)
if (a[i1-1]==b[j1-1] && a[i1-1]<a[i-1] && f[i1][j1]>max) max=f[i1][j1];
f[i][j]=max+1;
}
这样做的效率是O(n^4),明显是不行的。
重新看一下上面的方法,一个最大的问题就是数组的空间没有得到重复的利用。当
a[i]!=b[j]的时候,相应的空间就闲置了。如果能够利用闲置的空间来传递一些信
息,那效率就会有所提高。前面都是把a和b放在对等的地位的,现在考虑用a对b扫
描,然后再对得到的结果找LIS。 !!!!!!讲的很好
for(i=1;i<=l1;i++)
for(j=1;j<=l2;j++)
{
f[i][j]=f[i-1][j]; // 这里可以传递
if (a[i-1]==b[j-1])
{
max=0;
for(k=1;k<j;k++)
if (b[k-1]<b[j-1] && f[i][max]<f[i][k]) max=k;
/* 这里如果f[i][k]>0,因为b[k]<b[j],所以不可能是a[i-1]和b[k]匹配,所以只
可能是a[0,i-2]和其匹配,故符合公共递增子列的要求 */
if (f[i][max]+1>f[i][j]) f[i][j]=f[i][max]+1;
}
}
这里的复杂度是O(n^3),但还是不行。
考虑到匹配的时候a[i-1]==b[j-1],可以进一步简化推出LIS的过程。
for(i=1;i<=l1;i++)
for(j=1;j<=l2;j++)
{
f[i][j]=f[i-1][j];
k=0; //这里k的意义和上一个的k是一样的,注意k<=j
if (a[i-1]>b[j-1] && f[i][k]>f[i][j]) k=j;
if (a[i-1]==b[j-1] && f[i][j]<f[i][k]+1) f[i][j]=f[i][k]+1;
}
这段代码的复杂度为O(n^2),加上路径记录以后就能AC 2432了。
4.2021哈尔滨C题-colorful tree【启发式合并优化DP】
解析
有一个 \(O(n*m)\)的DP:
定义f[x][c]为x节点在已经染成c颜色的前提下,还需要染多少次颜色
定义f[x][0]为x节点没有预先染色的最少步数,根据定义可以知道:\(f[x][0]=min^n_{i=1}(f[x][i])\)
转移如下:\(f[x][c] = \sum_{v} min(f[v][c], f[v][0])\)
复杂度太大,过不去。
但是看到DP的第二维是一些点集,点集外部的是我们不需要的信息。
所以考虑使用启发式合并优化掉第二维,使用全局懒标记维护加法,实现起来比较繁琐。
(这一题最大的错觉是:可以把每个儿子两两之间合并,然后再赋值给x。这样是不对的吧?因为转移方程是枚举了所有的儿子之后再计算f[x][0])
不懂,挺妙的感觉。
启发式合并的大概思路:
模拟\(O(n^2)\)的DP,使用启发式模拟sum的过程,而不是两两合并的。
选取一个最大的儿子fx.(就像树上启发式合并一样),然后把其它儿子fy加到fx里面。
1. 如果fx和fy都具有颜色c:那么直接加就行了,但是需要注意,最大的儿子的f[fx][c]他不一定是小于f[fx][0]的,所以要取个min,代码有注释(int mna = ...这一段)
2. 如果fx具有颜色c,但是fy还没有:使用懒标记维护加法
3. 如果fy具有颜色c,但是fx还没有:那么之前合并的所有儿子都需要拿出f[i][0]次(这里我用sum累加起来就行了)
烦死了,懒标记就是难搞,老是出现思维逻辑绕不过去而导致的错误。
调了一天终于搞明白的代码:AC代码
还有一份一开始两两合并但是wa5的代码:WA代码
5. D2. Zero-One (Hard Version)【在贪心之后,DP最优子结构成立,可以优化成\(O(n^2)\)的区间DP】【\(O(n)\)做法】
首先D1的easy版本提醒你,当x>=y时,你应该怎么办:
- 当cnt=2时,且p[0]+1=p[1]: \(ans=min(x, 2 * y)\)
- 否则,\(ans=cnt/2*y\),因为一定可以两两匹配成功。 构造出来就行了:[1,n/2+1]、[2,n/2+2]...[n/2,n]这样匹配一定不会出现相邻情况。
然后我们考虑y>x的情况:
- 此时多了一种: min(len * x, y) 的可能,并且len一定是相邻的两个点同时消去,不然不是最优。
- 所以我们考虑: \(dp[l][r]=min(dp[l][r-2]+W_1, dp[l+2][r]+W_2, dp[l+1][r-1]+y)\)
- 成立原因:\(l和r\)不会同时匹配为\([l,ml]、[mr,r]\),因为这种情况略于\([l,r]、[ml,mr]\)匹配。前者代价一定是2*y(因为ml和l不相邻,mr和r不相邻,否则就是前两种情况之一了),后者代价是y+min(y, dis(ml, mr) * x)。所以从边界开始DP是合理的。
6.G - Row Column Sums 2【简化DP状态】
这道题就很难往DP方面想,想到DP之后,我还是不会优化状态数。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号