ACM散题习题库 2【持续更新】

习题101~200：

需要查询题目的请按 Ctrl-F。

（1）先用丑数筛筛出丑数【ll要换成__int128_t】

丑数筛一定要注意去重，不然可能一个数会出现2次以上。

ll uNum[maxn];
inline void initUgly(int n){
    priority_queue<ll,vector<ll>,greater<ll>>q;
    q.push(1);
    ll top = 0 , las = 1;
    while(top <= n){
        q.push(las*2);
        q.push(las*3);
        q.push(las*5);
        las = q.top(); //获取队列里最小的数作为第i个答案
        while(!q.empty() && las == q.top())q.pop();
        uNum[++top] = las;
    }
}

View Code

（2）再利用矩阵快速幂求解数列的第n项。

其实见到 f(x) = a*f(x-1) + b*f(x-2) 等类似的数列递推公式，都可以利用矩阵进行求解。

102：十进制快速幂 \ 欧拉降幂【牛客】

103：流水线调度【UVA690】

不是很懂题意，但是有一个很妙的灵感。

upd：题目中的程序不能够暂停，一旦开始，就只能不停走下去直到n个片段完成。

由于每个任务都必须是连续完成的，所有任务都是相同的，所以两两之间偏移量也是全部一样的。

（1）我们预处理出两个程序之间可行的偏移量。

（2）使用bitmask做标记，若一个bit = 1，就说明在这个时间点，程序需要使用这个单元。我们每一次考虑从第0位开始加入一个新的程序，那么最多也只会加到第n位，你可能会说，20*10，一共200个时间点，你这样做不就溢出了吗？

是的，的确是溢出了，但是这并不影响答案的正确性。因为溢出的位不会影响到0~n这些bit。

所以直接dfs即可。

104：树上机器人规划【BFS+状压+暴力枚举】

高质量的暴力来源于信心与实力，ok？

105：n个正方形覆盖问题【带点trick的二分】

很容易想到二分，关键在于怎么判断N个L*L的正方形是否能覆盖，这里选择一个一个正方形去覆盖，而最优的状态一定是作为四个顶点之一，所以这个答案书有四个分枝，复杂度O(4^N-1 * n * log(1e18))，N为正方形个数，因为N=3，所以也很快。

const int inf_int = 0x3f3f3f3f;
const ll  inf_ll  = 0x3f3f3f3f3f3f;
const ll maxn = 2e4+11, maxe = 1e4+11,mod = 1e9+7;

int n,used[maxn],tot;
PLL p[maxn];
ll L,R,mid;

inline void getBound(ll&lx,ll&ly,ll&rx,ll&ry){
    lx=ly=inf_int,rx=ry=-inf_int;
    for(int i = 1;i <= n;i++)if(!used[i]){
        lx = min(lx,p[i].fi); rx = max(rx,p[i].fi);// lx  rx
        ly = min(ly,p[i].se); ry = max(ry,p[i].se);// ly  ry
    }
}

inline int OK(){
    ll lx,ly,rx,ry;
    getBound(lx,ly,rx,ry);
    if(rx-lx>mid)return false;
    if(ry-ly>mid)return false;
    return true;
}

inline void fun(ll lx,ll ly,ll rx,ll ry,int tp){
    for(int i = 1;i <= n;i++){
        if(lx <= p[i].fi && ly <= p[i].se && rx >= p[i].fi && ry >= p[i].se)
            used[i] += tp;
    }
}

inline int check(int k){
    if(k==2)return OK();
    ll lx,ly,rx,ry;
    getBound(lx,ly,rx,ry);
    // 1 左下角
    fun(lx,ly,lx+mid,ly+mid,1);
    if(check(k+1))return true;
    fun(lx,ly,lx+mid,ly+mid,-1);
    // 2 右下角
    fun(rx-mid,ly,rx,ly+mid,1);
    if(check(k+1))return true;
    fun(rx-mid,ly,rx,ly+mid,-1);
    // 3 右上角
    fun(rx-mid,ry-mid,rx,ry,1);
    if(check(k+1))return true;
    fun(rx-mid,ry-mid,rx,ry,-1);
    // 4 左上角
    fun(lx,ry-mid,lx+mid,ry,1);
    if(check(k+1))return true;
    fun(lx,ry-mid,lx+mid,ry,-1);
    return false;
}

inline void solve()
{
    read(n);
    for(int i = 1,a,b;i <= n;i++){
        read(a,b);
        p[i] = mp(a,b);
    }
    L = 0,R = inf_ll,mid;
    while(L < R){
        mid = (L+R)>>1;
        me(used,0);
        if(check(0))R=mid;
        else L=mid+1;
    }
    printf("%d\n",L);
}

View Code

106：两亲性分子【计算几何+双指针+极坐标】

由于数据量为1000，可以O(n)枚举旋转轴，然后旋转记录答案，但是这个旋转的过程十分麻烦，看到一些大佬使用了这些技巧。

（1）由于黑白分别在轴的两侧，那么可以坐标轴对称一下，使得黑白在同一侧，那么分别求两侧的数量的问题转化为从L到R的扇形内部究竟有多少个黑点和白点

（2）由于每次枚举的点都不一样，所以考虑重新建系，然后极角排序，不要嫌麻烦而不重新建系

（3）双指针的过程也是一个麻烦的过程，关键在于枚举L，然后R指向180度的地方，这里使用叉乘判断是否在180以内，

注意（L!=R），这样就避免了出现了所有点在同一侧时导致的死循环问题。

107：Hash function【完美哈希】

（1）解法一：

首先了解到答案的范围是： [ n , mx - mn + 1] .

如果一个值m能作为base，那么 ai%m 的值不冲突。

如果 aj 和 ai 冲突了，那么就是 aj - ai = k*m ，即存在一个差值，并且m是这个差值的因子。

所以我们需要枚举两个元素之间的差值，但是又不需要完全枚举，因为如果当前的值是 ans ，那么小于 ans 的那些差值不需要去管。

催生出一个暴力而巧妙地解法，每一次都选一个数 ai ，然后二分出比他大 ans 的数 aj ，继续枚举 j~n ，取差值进行分解，对于小于 ans 的因子直接抹去，所以考虑枚举倍数k，然后 (aj-ai)/k < ans （不能取等号）时，直接退出循环。【再加上vis[ aj - ai ]判个重接可以过了】

（2）解法二：FFT。

108： J Journey among Railway Stations 【线段树维护】

维护一个节点，每个节点具有如下属性：

区间 [ l , r ] 中，在路上一共花费的时长 time
区间 [ l , r ] 中，从 L 之后出发可以保证经过每个station
区间 [ l , r ] 中，从 R 之前出发可以保证经过每个station
区间 [ l , r ] 中，从 l 出发，到 r ，是否可以经过每个station的标记 flag

109：Stack【构造合法序列 + 拓扑关系 + 单调栈】

先考虑一个简单的问题，如果把 1~n 的 bi 全都给出，那么将如何求解？

对于每个位置 i ，如果 1~i-1 已经形成了一个 b_i-1长的单调递增序列，那么第 i 的位置，形成的单调序列长度不可能超过

b_i-1+ 1 ，所以这是一个条件： b_i-1+ 1 >= bi ，如果不成立，直接输出-1即可。

那么给出全部 bi 之后，应该怎么求解呢？因为第 i-1 的位置已经给出长度了，而且我们也知道第 i 个位置的单调序列长度，所以，根据 bi 与 b_i-1的差值，可以求出第 i 个位置，栈弹出了多少个元素，所以直接向前找，找到 a_t< a_i的位置，这个时候，a_i就成为栈顶新的元素。

根据这里可以得出关系式：如果 a_t< a_i , 且 t 是离 i 最近的点，那么 t 会有一条指向 i 的边，这个时候直接建立拓扑关系。

然后根据上面建立的拓扑关系，倒序遍历边的集合即可。

为什么要倒序遍历呢？考虑 at < a_i-1 > ai ，那么 t 就会有一条指向 i-1 的边和指向 i 的边，但是因为我们是贪心地赋值【即从小到大赋值】，所以应该倒序遍历（边的数组），那么保证后面的点是比前面的点小的！

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f;
const ll maxn = 1e6 + 11, maxe = 4e5 + 11, mod = 1e9 + 7;
const lld eps = 1e-9;

int n, K, b[maxn], ans[maxn], top;
vector<vector<int>> e;

inline void topo(int x) {
  ans[x] = top++; // 倒序遍历
  for (int i = e[x].size() - 1; ~i; i--) topo(e[x][i]);
}

inline void solve() {
  read(n, K);
  e.assign(n + 1, vector<int>());
  for (int i = 1, t1, t2; i <= K; i++) {
    read(t1, t2), b[t1] = t2;
  }
  for (int i = 1; i <= n; i++) {
    if (!b[i])
      b[i] = b[i - 1] + 1;
    else if (b[i] > b[i - 1] + 1) {
      puts("-1");
      return;
    }
  }
  stack<int> s;
  s.push(0);
  for (int i = 1; i <= n; i++) {
    //de(b[i]);
    while (s.size() && b[s.top()] >= b[i]) s.pop();
    e[s.top()].emp(i), s.push(i);
  }
  topo(0);
  for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
  pln;
}

View Code

110 ： Girlfriend 【转换不等式得到两个实心球的方程，求两个实心球的体积交】

111：HDU - 6955_xor_sum 【01-trie】

一道比较模板的题目，当使用异或前缀和优化问题之后，我们枚举 r ，计算区间左端点 L，就变成选两个最近的数异或值大于k了，而两个数的异或值大于k我们可以使用trie维护。

（1）trie可以从一个集合中获取与x异或值最大的数【即x与{a1,a2,a3..}中选一个值异或得到的最大值】，也可以获取与x异或的值 大于某个值的数的个数【即x与{a1,a2,a3..}那些数异或之后大于、等于 k 】，①获取最大值需要一直走位互补的路径，如果不存在，才走同位的路径， ②而求大于某个值的个数，只需要统计有多少当 k 的第 i 位为 0 时，但是存在位互补的位置的个数即可。

（2）由于这道题要获取的是大于k的值中，离 r 最近的数，所以我们使用 pos 数组维护每个节点的值的下标index，这样我们枚举到这些值时，就可以max{ pos1 , pos2 ... }从而获得离 r 最近的数。

另外数组不要开小了

//#pragma GCC optimize(3,"inline","Ofast")
#include <bits/stdc++.h>
#define lowbit(x) (x & (-x))  //-为按位取反再加1
#define re register
#define mseg ((l + r) >> 1)
#define ls (ro << 1)
#define rs ((ro << 1) | 1)
#define ll long long
#define lld long double
#define uint unsigned int
#define ull unsigned long long
#define fi first
#define se second
#define pln puts("")
#define dbg(a...) fprintf(stderr, a)
#define deline cout << "-----------------------------------------" << endl
#define de(a) cout << #a << " = " << a << endl
#define de2(a, b) de(a), de(b), deline
#define de3(a, b, c) de(a), de(b), de(c), deline
#define de4(a, b, c, d) de(a), de(b), de(c), de(d), deline
#define emp(a) push_back(a)
#define iter(c) __typeof((c).begin())
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define arrdd array<double, 3>
#define me(x, y) memset((x), (y), sizeof(x))
#define mp make_pair
using namespace std;
/////快读
template <typename T>
inline void read(T &res) {  //
  ll x = 0, f = 1;
  char ch = getchar();
  while (ch != EOF && (ch < '0' || ch > '9')) {
    if (ch == '-') f = -1;
    ch = getchar();
  }
  while (ch != EOF && ch >= '0' && ch <= '9') {
    x = (x << 1) + (x << 3) + (ch ^ 48);
    ch = getchar();
  }
  res = x * f;
}
template <typename T, typename... Args>
inline void read(T &t, Args &...a) {
  read(t), read(a...);
}

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f;
const ll maxn = 1e5 + 11, maxe = 5e5 + 11, mod = 1e9 + 7;
const lld eps = 1e-9;

//初始节点为1
// 由于最大只会出现30次方，所以32倍搓搓有余
int tr[2][maxn << 5], n, k, f, top;
int pos[maxn << 5], ansL, ansR;

inline void insert(ll x, int p) {
  int ro = 1;
  for (ll i = 30; ~i; i--) {
    int t = ((1ll << i) & x) > 0;
    if (!tr[t][ro])
      ro = tr[t][ro] = ++top, tr[0][top] = tr[1][top] = 0, pos[top] = -1;
    else
      ro = tr[t][ro];
    pos[ro] = max(pos[ro], p);
  }
}

// 不仅要获取pre[i]^pre[j] >= k，而且还要求最短，这个是最麻烦的
inline int query(ll x, ll k) {
  int ro = 1, res = -1;
  for (ll i = 30; ~i; i--) {
    int t = (1ll << i) & k, w = ((1ll << i) & x) > 0;
    if (!t) {  // 如果k的第i位是0，那么使得这一位是1，就可以大于它。
      if (tr[w ^ 1][ro]) res = max(res, pos[tr[w ^ 1][ro]]);
      ro = tr[w][ro];
    } else {  // 如果k的第i位是1，那么只能沿x的反方向走,才能使得这一位是1
      ro = tr[w ^ 1][ro];
    }
    if (!ro) break;  // 直接退出
  }
  if (ro) res = max(res, pos[ro]);  // 存在等于的情况
  return res;
}

inline void solve() {
  ansL = -1, ansR = -1, top = 1;  // 1已经是根节点，所以top从1开始
  tr[0][1] = tr[1][1] = 0, pos[1] = -1;  // 初始化,排除上次测试的节点
  insert(0, 0);
  read(n, k), f = 0;
  for (ll i = 1, t; i <= n; i++) {
    read(t), f ^= t;
    int res = query(f, k);
    insert(f, i);
    if (res >= 0 &&
        (ansL < 0 || (ansR - ansL > i - res - 1 ||
                      (ansR - ansL == i - res - 1 && ansL > res + 1))))
      ansL = res + 1, ansR = i;
  }
  if (ansL != -1)
    printf("%d %d\n", ansL, ansR);
  else
    puts("-1");
}

int main() {
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  scanf("%d", &TEST);
  while (TEST--) solve();
}

/*

*/

View Code

112：I love counting 【莫队+trie维护】

理论上 n*sqrt(n)*logn ≈ 4e8 左右的复杂度，这不可能TLE呀，但是就是T了，是不是因为hdoj太慢了。。

int tr[maxn * 22][2], posCnt[maxn * 22];
queue<int> id;
inline int getID() {
  int ID = id.front();
  id.pop();
  return ID;
}

inline void initID() {
  for (re int i = 2; i <= maxn * 17; i++) id.push(i);
}

inline void insert(int x) {
  int ro = 1;
  for (re int i = 17; ~i; i--) {
    int w = (x >> i) & 1;
    if (!tr[ro][w]) tr[ro][w] = getID();
    ro = tr[ro][w];
    posCnt[ro]++;
  }
}

inline void remove(int x) {
  re int ro = 1;
  for (re int i = 17; ~i; i--) {
    int w = (x >> i) & 1, tmp = ro;
    posCnt[tr[ro][w]]--;
    ro = tr[ro][w];
    if (!posCnt[tr[tmp][w]]) id.push(tr[tmp][w]), tr[tmp][w] = 0;
  }
}

Trie的增删操作

用数据测过了。。。是对的，但是就是被卡在两秒，而std是1.2s左右

113: K - I love max and multiply 【二进制枚举子集】

这道题显然求出Ck数组就可以解决问题了，但是C怎么求？

①：其中 i & j >= k 是一个重大的突破点，这个式子说明 k 既是 i 的一个子集，又是 j 的一个子集，先来考虑简化的问题：令 k = i & j ，则有两种方法，一种是根据 k 来枚举i，j，另一种是根据 i ，j 来推出 k （逆向思维）

由于 i 和 j 是相互独立的，我们考虑通过分别枚举 i、j ，并且转移最大值。【枚举 i 中存在的bi】

②：这道题目十分可恶，竟然有负数存在，所以我们既要维护最小值，又要维护最大值，最后取4个值之中的最大乘积即可

114:C-Minimum grid_2021牛客暑期多校训练营3 (nowcoder.com) 【二分图最大匹配】

为了最小化权值，要么把尽可能多的格子填0，要么就把一个填了正整数的格子多重利用。

题解中把题目提出条件的最大值称为【限定值】

由于题目必定有解，所以所有行、列限定值中的最大值一定可以行列使用同一个，如果某一行、列填入了限定值，那么之后就不能填更大的数。

为了保证答案计算的一定是可行解，我们考虑把限定值排序，从大到小填进去，这样可以保证大的先被满足，小的不受影响。

而大的填法也是有技巧的，就是对于第 i 行的限定值为 a[ i ] ，我们一定要找一个限定值为 a[ i ] 的列，才能填进去【同时这个格子可以填数字】，这就要求我们把限定值相等的行列抽离出来，视为一个局部矩阵，而一个可以填数的格子就可以视为（行与列之间的边），然后跑一遍最大匹配，从而找出这个正整数被多重利用了多少次，然后 a[ i ] *（ cnt-maxPair ）就是填好这个局部矩阵的成本。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f;
const ll maxn = 1e6 + 11, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-4;

int n, m, k, com[maxn], vis[maxn], cnt[maxn];
int timeTop, valTop, a[maxn], b[maxn];
ll ans;
vector<vector<int>> e, s;

inline int DFS(int x) {
  if (vis[x] == timeTop) return false;
  vis[x] = timeTop;
  for (int &v : e[x]) {
    if (b[v] != a[x]) continue;
    if (!com[v] || DFS(com[v])) {
      com[v] = x;
      return true;
    }
  }
  return false;
}

inline void solve() {
  read(n, m, k);
  ans = 0;
  e.assign(n + 2, vector<int>());
  s.assign(k + 2, vector<int>());
  for (int t, i = 1; i <= n; i++) read(a[i]), s[a[i]].emp(i), cnt[a[i]]++;
  for (int t, i = 1; i <= n; i++) read(b[i]), cnt[b[i]]++;
  for (int x, y, i = 1; i <= m; i++) read(x, y), e[x].emp(y);
  for (int cur = k; ~cur; cur--) {
    int tmp = 0;
    for (int &x : s[cur]) {
      timeTop++;
      if (vis[x] != timeTop && DFS(x)) tmp++;
    }
    ans += 1LL * (cnt[cur] - tmp) * cur;
  }
  printf("%lld\n", ans);
}

View Code

115 ： black and white【矩阵转换为最小生成树 + 使用桶加速kruscal最小生成树】

由于每一行每一列都需要一个格子，即至少n+m-1个格子才能涂黑全部，所以可以想到行与列建树。

但是如果直接拿格子的权值【就是边权】进行排序，会自带一个logn的复杂度，这样会TLE。

然后看到题目对边权有了一个限制，也就是说，可以使用桶来从小到大装起来，然后从小到大遍历，这样就不用排序了。

【std用的是prim，朴素的prim复杂度是O(n^2)，由于这个图是完全图，所以完全可以使用朴素的prim，反而更快，而优先队列优化的prim复杂度是O(m*logn) 比朴素排序的kruscal快一点，但是由于logn的复杂度，不及朴素的prim，然而使用桶排，可以使得kruscal复杂度降到O(m) 】

116 : futa go 游戏【多变量的01背包】

首先对游戏从者做一次01背包，然后对装备做一次01背包，最后枚举两个背包的体积，以及选的从者个数和装备个数，这样记录答案即可。【可直接看pigeonG源码】

117: I love exam【多变量的01背包 + DP求最优解】

先对每个科目DP一次，然后再综合DP一次即可，注意下细节【我因为关了同步流wa了N久，人类未解之谜】

/// #pragma GCC optimize(3, "inline", "Ofast")
#include <bits/stdc++.h>
#define lowbit(x) (x & (-x))  //-为按位取反再加1
#define re register
#define mseg ((l + r) >> 1)
#define ls (ro << 1)
#define rs ((ro << 1) | 1)
#define ll long long
#define lld long double
#define uint unsigned int
#define ull unsigned long long
#define fi first
#define se second
#define pln puts("")
#define dbg(a...) fprintf(stderr, a)
#define deline cout << "-----------------------------------------" << endl
#define de(a) cout << #a << " = " << a << endl
#define de2(a, b) de(a), de(b), deline
#define de3(a, b, c) de(a), de(b), de(c), deline
#define de4(a, b, c, d) de(a), de(b), de(c), de(d), deline
#define emp(a) push_back(a)
#define iter(c) __typeof((c).begin())
#define ios_fast ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define arrdd array<double, 3>
#define me(x, y) memset((x), (y), sizeof(x))
#define mp make_pair
using namespace std;
/////快读
template <typename T>
inline void read(T &res) {  //
  ll x = 0, f = 1;
  char ch = getchar();
  while (ch != EOF && (ch < '0' || ch > '9')) {
    if (ch == '-') f = -1;
    ch = getchar();
  }
  while (ch != EOF && ch >= '0' && ch <= '9') {
    x = (x << 1) + (x << 3) + (ch ^ 48);
    ch = getchar();
  }
  res = x * f;
}
template <typename T, typename... Args>
inline void read(T &t, Args &...a) {
  read(t), read(a...);
}

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f;
const ll maxn = 311, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-4;

int n, m, d, p, f[55][555][5];
map<string, int> mpID;
string str;
vector<vector<PII>> s;
vector<vector<int>> dp;

inline void solve() {
  // 输入与初始化
  cin >> n, me(f, -1), mpID.clear();
  for (int i = 1; i <= n; i++) cin >> str, mpID[str] = i;
  cin >> m;
  s.assign(n + 2, vector<PII>());
  for (int i = 1, x, y; i <= m; i++) {
    cin >> str >> x >> y;
    s[mpID[str]].emp(mp(x, y));
  }
  cin >> d >> p;
  dp.assign(n + 2, vector<int>(d + 2, -1));
  // 开始计算每一个科目的01背包
  for (int i = 1; i <= n; i++) {
    dp[i][0] = 0;
    for (PII &it : s[i]) {
      for (int D = d; D >= it.se; D--) {
        if (dp[i][D - it.se] != -1)
          dp[i][D] = min(100, max(dp[i][D], dp[i][D - it.se] + it.fi));
      }
    }
  }
  // 开始综合全部科目，取最优
  f[0][0][0] = 0;
  for (int i = 1; i <= n; i++) {
    for (int D1 = d; ~D1; D1--) {  // D1 >= 0
      for (int D2 = d; D2 >= D1; D2--) {
        for (int j = 0; j <= p; j++) {
          if (dp[i][D1] >= 60) {  // 大于60，没有挂科！
            if (f[i - 1][D2 - D1][j] != -1)
              f[i][D2][j] = max(f[i][D2][j], f[i - 1][D2 - D1][j] + dp[i][D1]);
          } else if (dp[i][D1] >= 0) {  // 至少有一门挂科
            if (f[i - 1][D2 - D1][j] != -1)
              f[i][D2][j + 1] =
                  max(f[i][D2][j + 1], f[i - 1][D2 - D1][j] + dp[i][D1]);
          }
        }
      }
    }
  }
  //统计答案
  int ans = -1;
  for (int i = 1; i <= d; i++) {
    for (int j = 0; j <= p; j++) {
      ans = max(ans, f[n][i][j]);
    }
  }
  cout << ans << endl;
}

int main() {
  //freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  scanf("%d", &TEST);
  while (TEST--) solve();
}

/*

1
2
a b
10
a 10 1
a 10 1
a 10 1
a 10 1
a 10 1
b 10 1
b 10 1
b 10 1
b 10 1
b 10 1
10 2

*/

View Code

118： I love Tree 【树链剖分】

很容易看出是树链剖分，关键在怎么使用线段树维护。

线段树维护部分：

由于<h,t>这条树链形成的效果是：每个节点的权值增加： (x - h)^2 ，转换到logn个连续的区间 [ l , r ] 上就是 (x-l)^2 ，所以考虑维护 x^2 , h , h^2 三棵线段树（以及懒标记），最后计算sum权值即可【sum = x^2 - 2*x*h + h^2】。

实现部分：

由于两次DFS之后，节点从树上变成logn个连续的区间，所以主要难度在于update函数，因为udpate是分方向的【1 1 9 和 1 9 1 】带来的效果是不一样的，所以不能直接再套用普通的模板，我们这里选用求出 lca ，设更新的树链为<x,y>，那么我们先更新 x 到 lca ，并且记录这条<x,lca>的长度，以便后续update，最后再减去lca重复的计算即可。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f;
const ll maxn = 2e5 + 11, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-4;

ll n, q, tr[maxn << 2], tagx2[maxn << 2], tagxh[maxn << 2], tagh2[maxn << 2];
int son[maxn], sz[maxn], dfn[maxn], top[maxn], rk[maxn], dep[maxn];
int ls[maxn], rs[maxn], fa[maxn], cnt, f[maxn][20];
vector<vector<int>> e;

inline void preDFS(int x, int pre) {
  sz[x] = 1, fa[x] = pre, dep[x] = dep[pre] + 1;  // 深度是为了寻找lca
  for (int &v : e[x])
    if (v != pre) {
      preDFS(v, x);
      sz[x] += sz[v];
      if (sz[son[x]] < sz[v]) son[x] = v;
    }
}

// 获取 1 + 2^2 + 3^2 + ...
inline ll getX2(ll x) { return (x) * (x + 1) / 2 * (2 * x + 1) / 3; }
inline ll getX(ll x) { return (x) * (x + 1) / 2; }
inline void push_up(int ro) { tr[ro] = tr[ls[ro]] + tr[rs[ro]]; }
inline void push_down(int ro, ll l, ll r) {
  if (tagx2[ro] != 0) {
    tagx2[ls[ro]] += tagx2[ro], tagx2[rs[ro]] += tagx2[ro];
    tr[ls[ro]] += tagx2[ro] * (getX2(mseg) - getX2(l - 1));
    tr[rs[ro]] += tagx2[ro] * (getX2(r) - getX2(mseg));
  }
  if (tagxh[ro] != 0) {
    tagxh[ls[ro]] += tagxh[ro], tagxh[rs[ro]] += tagxh[ro];
    tr[ls[ro]] -= 2ll * tagxh[ro] * (getX(mseg) - getX(l - 1));
    tr[rs[ro]] -= 2ll * tagxh[ro] * (getX(r) - getX(mseg));
  }
  if (tagh2[ro] != 0) {
    tagh2[ls[ro]] += tagh2[ro], tagh2[rs[ro]] += tagh2[ro];
    tr[ls[ro]] += tagh2[ro], tr[rs[ro]] += tagh2[ro];
  }
  tagh2[ro] = tagxh[ro] = tagx2[ro] = 0;
}

inline void build(int ro, int l, int r) {
  if (l == r) {
    return;
  }
  ls[ro] = ++cnt, rs[ro] = ++cnt;
  build(ls[ro], l, mseg), build(rs[ro], mseg + 1, r);
  push_up(ro);
}

inline void getDFN(int x, int pre, int f) {
  dfn[x] = ++cnt, rk[cnt] = x;  // 记录dfn以及排第cnt的点是什么
  top[x] = f ? x : top[pre];
  if (!son[x]) return;
  getDFN(son[x], x, 0);
  for (int &v : e[x])
    if (v != pre && v != son[x]) {
      getDFN(v, x, 1);
    }
}

inline void update(int ro, int l, int r, ll h, ll x, ll y, ll tp) {
  if (y < x) return;
  if (x <= l && r <= y) {
    tr[ro] += tp * (getX2(r) - getX2(l - 1) - 2 * h * (getX(r) - getX(l - 1)) +
                    h * h);
    tagxh[ro] += tp * h, tagh2[ro] += tp * h * h, tagx2[ro] += tp;
    return;
  }
  push_down(ro, l, r);
  if (x <= mseg) update(ls[ro], l, mseg, h, x, y, tp);
  if (mseg < y) update(rs[ro], mseg + 1, r, h, x, y, tp);
  push_up(ro);
}

inline ll query(int ro, int l, int r, int x) {
  if (r < l) return 0;
  if (l == r) return tr[ro];
  push_down(ro, l, r);
  if (x <= mseg) return query(ls[ro], l, mseg, x);
  if (x > mseg) return query(rs[ro], mseg + 1, r, x);
  return 0;
}

inline void initLCA() {
  for (int i = 1; i <= n; i++) f[i][0] = fa[i];
  for (int i = 1; i <= 17; i++)
    for (int j = 1; j <= n; j++)
      if (f[j][i - 1]) f[j][i] = f[f[j][i - 1]][i - 1];
}

inline int getLCA(int x, int y) {
  if (dep[x] < dep[y]) swap(x, y);
  for (int i = 18; ~i; i--)  // 移到同一高度
    if (dep[x] >= (1ll << i) + dep[y]) x = f[x][i];
  if (x == y) return x;
  for (int i = 18; ~i; i--)  // 一起向上走
    if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
  return f[x][0];
}

inline void solve() {
  //输入与预处理
  read(n);
  e.assign(n + 2, vector<int>());
  for (int i = 1, x, y; i <= n - 1; i++) read(x, y), e[x].emp(y), e[y].emp(x);
  cnt = 0, preDFS(1, 0), getDFN(1, 0, 1);
  cnt = 1, build(1, 1, n);
  //初始化lca数组
  initLCA();
  //询问
  read(q);
  while (q--) {
    int op, x, y, h, len = 1;
    read(op);
    if (op == 1) {
      read(x, y);  // 根据树剖进行update
      if (x == y) {
        update(1, 1, n, 1, dfn[x], dfn[y], 1);
        continue;
      }
      int lca = getLCA(x, y), tag = 0;
      // de(lca);
      // 先处理 x到lca
      if (lca != x) {
        tag++;
        while (top[lca] != top[x]) {
          update(1, 1, n, dfn[x] + len, dfn[top[x]], dfn[x], 1);
          len += dfn[x] - dfn[top[x]] + 1;  // 累计添加的长度
          x = fa[top[x]];
        }
        update(1, 1, n, dfn[x] + len, dfn[lca], dfn[x], 1);
        len += dfn[x] - dfn[lca];
      }
      // 再处理lca到y的部分
      if (lca != y) {
        tag++;
        while (top[y] != top[lca]) {
          h = dep[lca] - dep[top[y]] - len + dfn[top[y]];
          update(1, 1, n, h, dfn[top[y]], dfn[y], 1);
          y = fa[top[y]];
        }
        h = dfn[lca] - len;
        update(1, 1, n, h, dfn[lca], dfn[y], 1);
      }
      if (tag == 2) update(1, 1, n, dfn[lca] - len, dfn[lca], dfn[lca], -1);
    } else {
      read(x), printf("%lld\n", query(1, 1, n, dfn[x]));
    }
  }
}

View Code

119：I love data structure【线段树维护矩阵tag】

这道题是很经典的线段树题目，而且2，3操作可以视为矩阵操作，所以可以使用矩阵乘法懒标记加速。【卡常卡了很久才进3s】

使用矩阵乘法，就想起普通的乘法+加法的线段树，矩阵乘法照样会影响加法的懒标记，所以在push_down函数里面，先进行矩阵乘法，再进行加法【细节点请看updateHelper函数】，最后再注意一下输出会出现负数的情况即可。

关于为什么矩阵乘法这么使用，可以用手算一下，看出 a_pre和 a_{cur 、} b_pre和 b_cur的关系，其实就是和这个矩阵懒标记有关。

然后加法的标记就很朴素了。

#pragma GCC optimize(3, "inline", "Ofast")
#include <bits/stdc++.h>
#define lowbit(x) (x & (-x))  //-为按位取反再加1
#define re register
#define mseg ((l + r) >> 1)
#define ls (ro << 1)
#define rs ((ro << 1) | 1)
#define ll long long
#define lld long double
#define uint unsigned int
#define ull unsigned long long
#define fi first
#define se second
#define pln puts("")
#define dbg(a...) fprintf(stderr, a)
#define deline cout << "-----------------------------------------" << endl
#define de(a) cout << #a << " = " << a << endl
#define de2(a, b) de(a), de(b), deline
#define de3(a, b, c) de(a), de(b), de(c), deline
#define de4(a, b, c, d) de(a), de(b), de(c), de(d), deline
#define emp(a) push_back(a)
#define iter(c) __typeof((c).begin())
#define ios_fast ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define arrdd array<double, 3>
#define me(x, y) memset((x), (y), sizeof(x))
#define mp make_pair
using namespace std;
/////快读
template <typename T>
inline void read(T &res) {  //
  ll x = 0, f = 1;
  char ch = getchar();
  while (ch != EOF && (ch < '0' || ch > '9')) {
    if (ch == '-') f = -1;
    ch = getchar();
  }
  while (ch != EOF && ch >= '0' && ch <= '9') {
    x = (x << 1) + (x << 3) + (ch ^ 48);
    ch = getchar();
  }
  res = x * f;
}
template <typename T, typename... Args>
inline void read(T &t, Args &...a) {
  read(t), read(a...);
}

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f;
const ll maxn = 2e5 + 11, maxe = 5e5 + 11, mod = 1000000007;
const lld eps = 1e-4;

struct Matrix {
  ll a[2][2];
  Matrix() { init(); };
  void clear() { a[0][0] = a[1][1] = a[1][0] = a[0][1] = 0; }
  void init() { a[0][0] = a[1][1] = 1, a[1][0] = a[0][1] = 0; }
  Matrix operator*(const Matrix &rhs) const {
    Matrix r;
    r.clear();
    for (int i = 0; i < 2; ++i)
      for (int j = 0; j < 2; ++j)
        for (int k = 0; k < 2; ++k)
          (r.a[i][j] += a[i][k] * rhs.a[k][j] % mod) %= mod;
    return r;
  }
  bool operator==(const Matrix &rhs) const {
    for (int i = 0; i < 2; ++i)
      for (int j = 0; j < 2; ++j)
        if (a[i][j] != rhs.a[i][j]) return false;
    return true;
  }
};

int n, m, a[maxn], b[maxn];
ll tra[maxn << 2], trb[maxn << 2], tra2[maxn << 2];
ll trab[maxn << 2], trb2[maxn << 2], atag[2][maxn << 2];
Matrix mtag[maxn << 2], rev, mul, E;

inline void push_up(const int &ro) {
  tra[ro] = (tra[ls] + tra[rs]) % mod, trb[ro] = (trb[ls] + trb[rs]) % mod;
  tra2[ro] = (tra2[rs] + tra2[ls]) % mod,
  trb2[ro] = (trb2[ls] + trb2[rs]) % mod;
  trab[ro] = (trab[ls] + trab[rs]) % mod;
}

inline void updateHelper(const int &ro, const Matrix &mt) {
  // 更新a，b
  re ll tmpA = (mt.a[0][0] * tra[ro]) % mod + (mt.a[1][0] * trb[ro]) % mod;
  re ll tmpB = (mt.a[0][1] * tra[ro]) % mod + (mt.a[1][1] * trb[ro]) % mod;
  // 加法tag也要更新 [ 最重要的地方！！！！！！！！！ ]
  re ll tagA =
      (mt.a[0][0] * atag[0][ro]) % mod + (mt.a[1][0] * atag[1][ro]) % mod;
  re ll tagB =
      (mt.a[0][1] * atag[0][ro]) % mod + (mt.a[1][1] * atag[1][ro]) % mod;
  // 更新 a2，b2，ab
  re ll tmpA2 = (mt.a[0][0] * mt.a[0][0] % mod * tra2[ro] % mod) % mod +
                (2 * mt.a[1][0] * mt.a[0][0] % mod * trab[ro] % mod) % mod +
                (mt.a[1][0] * mt.a[1][0] % mod * trb2[ro] % mod) % mod;
  re ll tmpB2 = (mt.a[0][1] * mt.a[0][1] % mod * tra2[ro] % mod) % mod +
                (2 * mt.a[1][1] * mt.a[0][1] % mod * trab[ro] % mod) % mod +
                (mt.a[1][1] * mt.a[1][1] % mod * trb2[ro] % mod) % mod;
  re ll tmpAB =
      ((mt.a[0][0] * mt.a[0][1] % mod * tra2[ro] % mod) % mod +
       ((mt.a[1][0] * mt.a[0][1] % mod + mt.a[0][0] * mt.a[1][1] % mod) *
        trab[ro] % mod) +
       (mt.a[1][0] * mt.a[1][1] % mod * trb2[ro] % mod) % mod);
  // 更新mtag
  mtag[ro] = mtag[ro] * mt;
  atag[0][ro] = tagA % mod,
  atag[1][ro] = tagB % mod;  // 加法标记 也要更新
  //赋值
  tra[ro] = tmpA % mod, trb[ro] = tmpB % mod, trab[ro] = tmpAB % mod;
  tra2[ro] = tmpA2 % mod, trb2[ro] = tmpB2 % mod;
}

inline void addHelper(int ro, const int &tag, const ll &len, const ll &val) {
  if (!tag) {  // 0 表示对 A 操作
    re ll tmpA = (tra[ro] + len * val % mod) % mod;
    re ll tmpA2 = ((tra2[ro] + (2 * tra[ro] % mod * val % mod)) % mod +
                   (len * val % mod * val % mod));
    re ll tmpAB = (trab[ro] + val * trb[ro] % mod) % mod;
    trab[ro] = tmpAB % mod, tra[ro] = tmpA % mod, tra2[ro] = tmpA2 % mod;
  } else {  // 1 表示对 B 操作
    re ll tmpB = (trb[ro] + len * val % mod) % mod;
    re ll tmpB2 = (trb2[ro] + 2 * trb[ro] * val % mod) +
                  (len * val % mod * val % mod) % mod;
    re ll tmpAB = trab[ro] + val * tra[ro] % mod;
    trab[ro] = tmpAB % mod, trb[ro] = tmpB % mod, trb2[ro] = tmpB2 % mod;
  }
  // 更新tag
  atag[tag][ro] = (atag[tag][ro] + val) % mod;
}

inline void push_down(int ro, int l, int r) {
  if (!(mtag[ro] == E)) {
    updateHelper(ls, mtag[ro]), updateHelper(rs, mtag[ro]);
    mtag[ro].init();
  }
  if (atag[0][ro]) {
    addHelper(ls, 0, mseg - l + 1, atag[0][ro]),
        addHelper(rs, 0, r - mseg, atag[0][ro]);
    atag[0][ro] = 0;
  }
  if (atag[1][ro]) {
    addHelper(ls, 1, mseg - l + 1, atag[1][ro]),
        addHelper(rs, 1, r - mseg, atag[1][ro]);
    atag[1][ro] = 0;
  }
}

inline void build(int ro, int l, int r) {
  if (l == r) {
    mtag[ro].init(), atag[0][ro] = atag[1][ro] = 0;
    tra[ro] = a[l] % mod, trb[ro] = b[l] % mod,
    trab[ro] = (1LL * a[l] * b[l]) % mod;
    tra2[ro] = (1LL * a[l] * a[l]) % mod;
    trb2[ro] = (1LL * b[l] * b[l]) % mod;
    return;
  }
  build(ls, l, mseg), build(rs, mseg + 1, r), push_up(ro);
}

inline void updateMatrix(int ro, int l, int r, int s, int e, const Matrix &mt) {
  if (s <= l && r <= e) {
    updateHelper(ro, mt);
    return;
  }
  push_down(ro, l, r);
  if (s <= mseg) updateMatrix(ls, l, mseg, s, e, mt);
  if (mseg < e) updateMatrix(rs, mseg + 1, r, s, e, mt);
  push_up(ro);
}

inline void addValue(int ro, int l, int r, int s, int e, const int &tag,
                     const ll &val) {
  if (s <= l && r <= e) {
    addHelper(ro, tag, r - l + 1, val);
    return;
  }
  push_down(ro, l, r);
  if (s <= mseg) addValue(ls, l, mseg, s, e, tag, val);
  if (mseg < e) addValue(rs, mseg + 1, r, s, e, tag, val);
  push_up(ro);
}

inline ll query(int ro, int l, int r, int s, int e) {
  if (s <= l && r <= e) return trab[ro] % mod;
  push_down(ro, l, r);
  ll ans = 0;
  if (mseg >= s) ans = (ans + query(ls, l, mseg, s, e)) % mod;
  if (mseg < e) ans = (ans + query(rs, mseg + 1, r, s, e)) % mod;
  return ans;
}

inline void solve() {
  //输入
  read(n);
  for (int i = 1; i <= n; i++) read(a[i], b[i]);
  //预处理rev和mul
  rev.a[0][0] = rev.a[1][1] = 0, rev.a[0][1] = rev.a[1][0] = 1;
  mul.a[0][0] = mul.a[0][1] = 3, mul.a[1][0] = 2, mul.a[1][1] = -2;
  //建树
  build(1, 1, n);
  //询问
  read(m);
  while (m--) {
    ll op, tag, l, r, v, x, y;
    read(op);
    if (op == 1) {
      read(tag, l, r, x), addValue(1, 1, n, l, r, tag, x);
    } else if (op == 2) {
      read(l, r), updateMatrix(1, 1, n, l, r, mul);
    } else if (op == 3) {
      read(l, r), updateMatrix(1, 1, n, l, r, rev);
    } else {
      read(l, r), printf("%lld\n", (query(1, 1, n, l, r) + mod) % mod);
    }
  }
}

int main() {
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  // cin >> TEST;
  while (TEST--) solve();
}

/*

 */

View Code

120：无根树拆点【换根DP+组合数学】

呜呜呜，这个题就算不换根的组合数学也很难吧！！

关键思想在于：定义 \( f_{x} \) 为以x为根的子树拆点的总数，难点在于怎么合并。

首先把拆点转化为一个序列，也就是有多少种合法的序列，合并的过程其实就是把不同序列合并而已，使用排列数即可，然后同一棵子树上的序列不进行排列。

假设已经计算出来 \( f_{v} \)，那么 \( f_{x} = C^{sz_{v}}_{current-sz_{x}-1} * f_{v} \)

牛客题解【十分详细】换根DP的思想在于：把答案移动到其它节点是，答案会出现怎么样的变化，这样，我们只需要计算出一个节点的答案，其它节点的答案都可以通过第一个节点转移出来。

题解中说到，这个问题等价于 求拓扑排序的个数【 拓扑排序，在有向无环图中，当且仅当某个节点的所有父节点都被遍历完（入度变成0），这个节点才会放进队列】，这个我是没有理解的，因为一个在树上，一个在有向图中。

关于组合数学部分，考虑 f[x] 为删除以 x 为根的子树，那么我们可以从 x 的子节点进行合并，相当于把几个排序固定的序列进行合并，【直接把同一颗子树的节点视为同一种颜色的球】，所以根据此类问题（如： 4个红球，3个白球的排列数 = C（7，3） = 7！/（3！ * 4！）。）可以计算出来。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f;
const ll maxn = 2e5 + 11, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-4;

ll n, m, sz[maxn], f[maxn], A[maxn], invA[maxn];
vector<vector<int>> e;

#define inv(x) (qpow(x, mod - 2, mod) % mod)
inline ll qpow(ll x, ll y, ll p) {
  ll res = 1;
  while (y) {
    if (y & 1) res = (res * x) % p;
    x = (x * x) % p, y >>= 1;
  }
  return res;
}

inline void init() {
  invA[1] = A[0] = A[1] = invA[0] = 1;
  for (ll i = 2; i < maxn; i++) {
    A[i] = (A[i - 1] * i) % mod;
    invA[i] = inv(A[i]);
  }
}

// C(x,y)
inline ll C(ll x, ll y) { return A[x] * invA[y] % mod * invA[x - y] % mod; }

inline int DFS(int x, int fa) {
  f[x] = sz[x] = 1;
  for (int &v : e[x])
    if (v != fa) {
      sz[x] += DFS(v, x);
      f[x] = (f[x] * f[v] % mod * C(sz[x] - 1, sz[v]) % mod) % mod;
    }
  return sz[x];
}

inline void DP(int x, int fa) {
  if (fa) {
    // 首先从上到下遍历，并且转移答案【所以父节点的答案已经完全计算】
    // 考虑去掉该节点对父节点答案的影响，除去f[x]以及除去排列组合C（n-1,sz[x]）   
    // 因为父节点的答案是完全的，所以除的时候取n作为底，n-1是因为x作为根，那就一定放在最后，可以不考虑进去排列
    // 最后计算答案，因为以x为根节点，所以最后一次合并之后sz==n，所以乘上C(N-1,n-sz[x])
    // n-sz[x] 为父节点一侧的节点数量
    ll tmp = f[fa] * inv(f[x]) % mod * inv(C(n - 1, sz[x])) % mod;
    f[x] = (f[x] * tmp % mod * C(n - 1, n - sz[x]) % mod + mod) % mod;
  }
  for (int &v : e[x])
    if (v != fa) DP(v, x);
}

inline void solve() {
  read(n);
  e.assign(n + 1, vector<int>());
  for (int i = 1, x, y; i < n; i++) read(x, y), e[x].emp(y), e[y].emp(x);
  DFS(1, 0);
  //de(f[1]);
  DP(1, 0);
  ll ans = 0;
  for (int i = 1; i <= n; i++) ans = (ans + f[i]) % mod;
  printf("%lld\n", ans);
}

View Code

121: 无根树简单路径涂色【树形DP+换根DP】

122：Road Discount 【】

123: Increasing Subsequence 【贡献分治 + 权值单调栈】

题设a为给出的排列，定义 f [ a[ i ] ] 为a[ i ] 为末尾的数量，可以看出，a[ i ] 可以接到a[ j ]前面，当且仅当 [ i , j ] 区间中，不存在一个数 x ， a[ i ] < x < a[ j ] 。这样定义的话，可以想到一个朴素的DP，O(n^2)的复杂度。

由于只有左边的数是对右边有贡献的，所以我们考虑分治，对于一个区间 [ L , R ] , 我们先计算出 [ L , mid ] 区间内的数对 [ mid+1 , R] 区间内的数的贡献，然后再计算 [ mid + 1 ， R ] 自身的贡献。

所以关键在于怎么维护求贡献的过程。

先谈谈需求，对于右边的一个数 a[ i ] ，在[ mid + 1, i ] 之间找到一个小于 a[ i ]的最大值【仅次小于a[i]的值，我们记为mn】，那么这样我们就可以对左边 [ L , mid ] 区间进行约束，我们只需要找到 a[ Li ] ... a[ Lj ] 这个递减序列，而且值域在 { mn , a[ i ] }之间，求一下和就可以转移了。

而对于我们的需求，是这样的问题：

（1）给出一个序列ai... ，对于一个 i ，我们要找到 i 之前的，且小于a[ i ]的最大值。

（2）如何在左区间找到这样的一个递减序列。

而std给出的权值单调栈的做法，【因为它利用权值排序，使得有效区间永远是中间部分，而两边无效的被pop掉】，解决了这样的问题。【妙啊】

【DP一开始要初始化数组，我利用单调栈让那些一定是序列开头的数字，初始化为 1 】

int n, m, a[maxn];
ll f[maxn];

inline void DP(int l, int r) {
  if (l == r) return;  // 自己对自己是不会有贡献的
  int m = (l + r) >> 1;
  DP(l, m);
  vector<ll> sum(1, 0);
  vector<int> pos(r - l + 1), lst, rst;
  iota(pos.begin(), pos.end(), l);
  sort(pos.begin(), pos.end(), [&](int i, int j) { return a[i] < a[j]; });
  for (int &i : pos) {
    if (i <= m) {
      while (lst.size() && lst.back() < i) sum.pop_back(), lst.pop_back();
      lst.emp(i), sum.emp((sum.back() + f[a[i]]) % mod);
    } else {
      while (rst.size() && rst.back() > i) rst.pop_back();
      if (lst.empty()) continue;
      int id = rst.empty() ? 0 : partition_point(lst.begin(), lst.end(), [&](int x) {
        return a[x] < a[rst.back()];
      }) - lst.begin();
      f[a[i]] = (f[a[i]] + (sum.back() - sum[id] + mod)) % mod , rst.emp(i);
    }
  }
  DP(m + 1, r);
}

inline void solve() {
  read(n);
  for (int i = 1; i <= n; i++) read(a[i]), f[i] = 0;
  f[n + 1] = 0, a[n + 1] = n + 1;
  vector<int> st;
  for (int i = 1; i <= n; i++) {
    while (st.size() && st.back() > a[i]) st.pop_back();
    if (st.empty()) f[a[i]] = 1;
    st.emp(a[i]);
  }
  DP(1, n + 1);
  printf("%lld\n", f[n + 1]);
}

View Code

124 : DMST 有向最小生成树【左偏树维护DMST 】

125: King of range 【单调队列】

对于任意一个 L = i （i <= n），我们找出一个 R，使得 [ L , R ]这个区间的极差大于k，那么对答案的贡献就是（n+1-R），所以问题的关键在于计算 Ri 数组。

我们要把握住问题的关键，问题不是要我们求与 ai 相差 k 的数，而是关注在每一个区间上面，这样就会有一个十分重要的性质：

对于 1~n 中的任意一个 i ， Ri 数组一定单调不减【这跟在R右移的过程中，极差的单调不减性质有关】，所以我们找到一个 Ri 之后，就可以直接将 Li 右移一个位置，然后 Ri 一定不会回退。【有点像双指针】

但是复杂度要求十分严格，我们需要动态地维护 [ Li ， Ri ] 区间内的最大、最小值，从而O(1)判断区间极差是否满足大于k。

由于极差的单调不减，我们考虑使用单调队列维护【最大值与最小值（方法是维护一个最大值的递减序列，维护一个最小值的递增序列，保证最新而且最大 / 小的值能保留下来）】，但是为了维护的是【最小的Ri】，所以我们要时刻从队首 pop 出离 Li 最远的元素，然后直到区间极差不大于k，那么最后留下的 last 值，就是离 Li 最近的 Ri 。

然后根据 Ri 累计答案即可

【std维护的是最大的 Li，方式调转，但是解题的思路一致】

int n, m, k, a[maxn];
ll ans;
int qmx[maxn], qmn[maxn], L1, L2, R1, R2, last;

inline void solve() {
  read(n, m);
  for (int i = 1; i <= n; i++) read(a[i]);
  while (m--) {
    read(k);
    ans = L1 = R1 = R2 = L2 = 0, last = n + 1;
    for (int i = n; i; --i) {
      while (L1 < R1 && a[qmn[R1 - 1]] > a[i]) R1--;
      qmn[R1++] = i;
      while (L2 < R2 && a[qmx[R2 - 1]] < a[i]) R2--;
      qmx[R2++] = i;
      while (L1 < R1 && L2 < R2 && a[qmx[L2]] - a[qmn[L1]] > k) {
        if (qmn[L1] > qmx[L2]) last = qmn[L1++];
        else  last = qmx[L2++];
      }
      ans += n + 1 - last;
    }
    printf("%lld\n", ans);
  }
}

View Code

126：boxes【概率+思维】

考虑直接求，对于每一个hints，即给出黑球个数，0~n ，黑球个数的概率是： C_nⁱ * (0.5ⁿ) ，然后对于每个黑球个数，我们还要计算出在这个条件之下，需要开箱子的个数，计算公式是： i ~ n-i+1 为可能开箱子的个数，对于每个 i （记x为黑球个数），因为要保证最后取的是黑：C_i^x-1 * preSum[i]+ C_i+1^x-1 *preSum[i+1] + ..... + C_n-i^x-1 *preSum[n-i]+ ( C_n-i+1^x-1 + 1)*preSum[n-i+1] , 最后加一是因为会有出现全部剩下黑球的情况。这样计算复杂度是 O（n方）的，直接爆炸。

换一个思维，我们考虑每个箱子形成的是一个随机的 01 序列，我们可以确定答案，当且仅当我们开完 i 个箱子之后，i+1~n这个区间内的颜色都是一致的。

逆向思维：我们不考虑每个箱子开的概率是多少，反之，这个概率等于（1 - 不会被打开的概率）。

因为 i~n 全0、全1时，i不需要被打开。

所以问题转换为，i~n这个为全0，全1时的概率是多少。

计算方法： i~n 一共有 n-i+1个数字，使得他们相同的概率是 (1 / 2^n-i+1) ，但是相同又有 0 或者1，所以乘上2， p = (1 / 2^n-i)，

所以答案就是： ans = ∑ wi*(1 / 2^n-i)。

127: Book shop 【树链剖分】

128：独钓寒江雪【DP+hash判断树是否同构】

129：Yazid新生舞会【思维 + n阶前缀和】

题目描述：求多少个子区间符合题目条件，题目条件是：子区间内众数数量多于区间长度一半【题解】

（1）单独考虑每个数对答案的贡献，转移到数学式子上就是 2*Sj - j < 2*Si - i

（2）写下每个数的 2*Si - i 数列，寻找到每段递减的规律，所以每一段统一考虑即可

（3）但是求和的时候有需要对区间求前缀和，所以考虑二维前缀和

综上，可以使用线段树区间修改+二维前缀和求解

但是，为了更加快，使用树状数组单点修改+三维前缀和求贡献。【注意细节，由于（1）中的式子是严格不等号的，所以树状数组要-1】

ll a[maxn], b[maxn], c[maxn], n, m, w, lim, sf, ans;
vector<vector<int>> s;

inline void add(ll i, int sig) {
  for (ll tmp = i; i <= lim; i += lowbit(i))
    a[i] += sig, b[i] += sig * tmp, c[i] += sig * tmp * tmp;
}

inline ll sum(ll x) {
  ll f1 = 0, f2 = 0, f3 = 0, tx = x;
  while (x > 0) {
    f1 += (tx * tx + 3 * tx + 2) * a[x];
    f2 += b[x] * (2 * tx + 3);
    f3 += c[x];
    x -= lowbit(x);
  }
  return (f1 - f2 + f3) / 2;
}

inline void solve() {
  read(n, m), lim = 2 * n + 1, sf = n + 1, ans = 0;
  s.assign(n + 2, vector<int>()), me(a, 0), me(b, 0), me(c, 0);
  for (int i = 1; i <= n; i++) read(w), s[w].emp(i);
  for (int i = 0; i < n; i++) {
    if (s[i].empty()) continue;
    s[i].emp(n + 1);
    add(sf + 1, -1), add(sf - s[i][0] + 1, 1);
    for (int j = 0; j < s[i].size() - 1; j++) {
      int x = sf - s[i][j + 1] + 2 * j + 3, y = sf - s[i][j] + 2 * j + 2;
      ans += sum(y - 1) - sum(x - 2);   
      // 别忘了多减一个1，因为题目是 < 严格小于号，但是树状数组会求等号
      add(y + 1, -1), add(x, 1);
    }
    for (int j = 0; j < s[i].size() - 1; j++) {
      int x = sf - s[i][j + 1] + 2 * j + 3, y = sf - s[i][j] + 2 * j + 2;
      add(y + 1, 1), add(x, -1);
    }
    add(sf + 1, 1), add(sf - s[i][0] + 1, -1);
  }
  printf("%lld\n", ans);
}

View Code

130：Defend your country【思维 + 割点 + 点双连通分量】

（1）求出所有的割点，使用dfs求出割点去除之后，所有联通块的奇偶性，如果全是偶数，那么就和最小值对比，更新合法最小值。【注意啊，无向图维护的sz数组在割点可以使用，其意义为：割点所连的双联通分量的大小，如果不是割点，则无意义（此时遍历的图的部分是一颗树的样子）】

（2）如果不是割点，那么直接更新最小值即可。

int n, m, dfn[maxn], low[maxn];
int dfncnt, cut[maxn], sz[maxn];
ll ans, a[maxn], mn;
vector<vector<int>> e;

inline void tarjan(int x, int fa) {
  dfn[x] = low[x] = ++dfncnt, sz[x] = 1, cut[x] = 0;
  for (int &v : e[x]) {
    if (v == fa) continue;
    if (!dfn[v]) {
      tarjan(v, x), sz[x] += sz[v];
      low[x] = min(low[x], low[v]);
      if (low[v] >= dfn[x]) {
        if ((fa || e[x].size() > 1) && !cut[x]) cut[x] = 1;
        if (cut[x] == 1 && (sz[v] & 1)) cut[x] = 2;
      }
    } else {
      low[x] = min(low[x], dfn[v]);
    }
  }
}

inline void solve() {
  read(n, m), ans = mn = dfncnt = 0;
  e.assign(n + 2, vector<int>());
  for (int i = 1; i <= n; i++) {
    read(a[i]), dfn[i] = 0;
    ans += a[i], mn = max(mn, a[i]);
  }
  for (int i = 1, x, y; i <= m; i++) read(x, y), e[x].emp(y), e[y].emp(x);
  if (n % 2 == 0) {
    printf("%lld\n", ans);
    return;
  }
  for (int i = 1; i <= n; i++)
    if (!dfn[i]) tarjan(i, 0);
  for (int i = 1; i <= n; i++)
    if (cut[i] < 2) mn = min(mn, a[i]);
  printf("%lld\n", ans - 2 * mn);
}

View Code

131: 书架【DP+数据结构】

定义dp[i]为 1~i 所需要的最小宽度，然后得出转移公式：

\( dp[i] = min\!_{j,i-1}( max_{k=(j+1,i)}(h_{k}) + dp[j-1] ) \)

所以难题就出在这个转移过程。

（1）考虑使用线段树，设 L 为使得 \( sum[i] - sum[L-1] <= m \)的最右位置，那么我们只需要询问 \( [L-1，i-1] \) 区间内最优的答案，这个完全可以使用线段树维护最小值，然后考虑更新h，如果我们每一次都直接把 \( h_{i} \) 直接区间update，会TLE的，根据h的影响范围更新就好，如果定义 pre_i为大于 \( h_{i} \) 的最后位置，那么这个影响范围就是 \( [pre_{i} , i] \) ，然后直接维护答案就好。【为了在线段树上表示出 \( dp_{0} \) 我把区间整体向右移动1位，有时候转移方程会查询到 \( dp_{0} \) 所以必须考虑到第0位的情况】

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 1e5 + 3, maxe = 5e5 + 11, mod = 1e6;
const lld eps = 1e-8;

ll a[maxn], s[maxn], tr[maxn << 2], ans, sum[maxn];
ll mh[maxn << 2], dp[maxn << 2], th[maxn << 2];
int n, m, L, top, p[maxn];

inline void push_down(int ro) {
  if (th[ro]) {
    th[rs] = max(th[rs], th[ro]), th[ls] = max(th[ls], th[ro]);
    mh[rs] = max(mh[rs], th[ro]), mh[ls] = max(mh[ls], th[ro]);
    tr[rs] = mh[rs] + dp[rs], tr[ls] = mh[ls] + dp[ls];
  }
}

inline void updateDP(int ro, int l, int r, int x, ll v) {
  if (l > r || r <= 0) return;
  if (l == r) return (tr[ro] = mh[ro] + (dp[ro] = v)), void();
  push_down(ro);
  x <= mseg ? updateDP(ls, l, mseg, x, v) : updateDP(rs, mseg + 1, r, x, v);
  tr[ro] = min(tr[ls], tr[rs]);
}

inline void updateH(int ro, int l, int r, int s, int e, ll v) {
  if (l > r || r <= 0) return;
  if (l == r) {
    mh[ro] = max(mh[ro], v), th[ro] = max(th[ro], v), tr[ro] = mh[ro] + dp[ro];
    return;
  }
  push_down(ro);
  if (s <= mseg) updateH(ls, l, mseg, s, e, v);
  if (mseg < e) updateH(rs, mseg + 1, r, s, e, v);
  tr[ro] = min(tr[ls], tr[rs]);
}

inline ll query(int ro, int l, int r, int s, int e) {
  if (r <= 0 || l > r) return 0;
  if (s <= l && r <= e) return tr[ro];
  push_down(ro);
  ll ans = inf_ll;
  if (s <= mseg) ans = min(ans, query(ls, l, mseg, s, e));
  if (mseg < e) ans = min(ans, query(rs, mseg + 1, r, s, e));
  return ans;
}

inline void solve() {
  read(n, m), me(dp, inf_ll), me(mh, 0);
  for (int i = 2; i <= n + 1; i++) {
    read(a[i]), sum[i] = sum[i - 1] + a[i];
    while (top && a[s[top - 1]] <= a[i]) top--;
    if (top)
      p[i] = s[top - 1];
    else
      p[i] = 2;
    s[top++] = i;
  }
  updateDP(1, 1, n + 1, 1, 0), L = 1;
  for (int i = 2; i <= n + 1; i++) {
    while (sum[i] - sum[L - 1] > m) L++;
    updateH(1, 1, n + 1, p[i] - 1, i - 1, a[i]);
    ans = query(1, 1, n + 1, L - 1, i - 1);
    updateDP(1, 1, n + 1, i, ans);
  }
  printf("%lld\n", ans);
}

View Code

132：xay loves trees 【后序映射到连续区间 + 树状数组+后序用于判断祖先节点与子孙节点的遍历关系】

题目描述：给你两棵树，要求你从1~n中选一些节点出来做成集合，使得这些节点中任选两个点u，v。（在第一棵树上）都有一个点是另一个点的祖先，（第二棵树上）u和v互相不是对方祖先。

转化问题：任意两个节点都存在一个点是祖先，那么这种关系很显然就是一条树链，所以这个集合必须是第一棵树上的某一条链。第二个条件呢显然就是这个集合中的任意两个点不在同一条链上。

考虑到是否在同一条链上的问题，这个问题十分抽象，除了暴力很难快速解决，所以考虑转化到连续的序列上。

有请出我们的后序遍历的性质： u节点和u节点的子树在区间上是连续的，并且在区间 \( [ dfn[u]-sz[u]+1, dfn[u] ] \) 上！

我们考虑dfs第一棵树，枚举 1~n 个节点，枚举到u时，定义 h_u为 \( h_{u} \) 到 u 的树链上是合法集合。【即hu到u的所有节点在第二棵树上不可能在同一条链上】

那么怎么判断呢？

情况1：u作为别人的子孙节点

　　我们给 [ h_u~fa_u] 的子树（第二棵树）的所有节点 +1，如果 u 的权值大于 0 ，说明u在前面那些节点的子树里，显然不符合条件　2 。

情况2：u作为别人的祖先节点

　　我们给 [ h_u~fa_u] 的子树（第二棵树）的所有节点 +1，然后查询u的子树中是否存在一个节点的权值大于0，如果有大于0的，说明 [ h_u~fa_u] 的树链中，存在一个点在 u 的子树内，不符合条件

所以当且仅当 [ h_u~fa_u] 的子树都+1，但是u的子树仍然为0的情况下，u的合法集合才能延伸到 h_u

最后用树状数组 + 二阶前缀和就可以解决问题了

奇怪的是，这题暴力add，暴力del都可以通过，然而添加了一个小贪心竟然wa了，贪心如下：

如果当前刷到的树链是 \( [ l , r ] \) ，答案是ans ，如果 \( ans > r-l+1 \) 且 u的子树不为0，那么就算计算出u节点的合法树链也不会更新答案，所以直接使得 l++,r++ 就算了。【不知道wa了哪里，如果是对的话，复杂度可以优化到\( O(nlogn) \)】

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 3e5 + 3, maxe = 5e5 + 11, mod = 1e6;
const lld eps = 1e-8;
 
int n, m, f1[maxn], f2[maxn], ans, sz[maxn];
int dfn[maxn], st[maxn], top, totdfn;
vector<vector<int>> e, fe;
 
inline void add(int x, int v) {
  for (int i = x; i > 0 && i <= n; i += lowbit(i)) {
    f1[i] += v, f2[i] += (x - 1) * v;
  }
}
 
inline int sum(int x) {
  ll res = 0;
  for (int i = x; i > 0; i -= lowbit(i)) res += x * f1[i] - f2[i];
  return res;
}
 
inline void pre_dfs(int x, int fa) {
  sz[x] = 1;
  for (int &v : fe[x])
    if (v != fa) pre_dfs(v, x), sz[x] += sz[v];
  dfn[x] = ++totdfn;
}
 
inline void las_dfs(int x, int fa, int l, int r) {
  st[r] = x;
  int tl = dfn[x] - sz[x], tr = dfn[x], preL = l;
  while (sum(tr) - sum(tl)) {
    add(dfn[st[preL]] + 1, 1), add(dfn[st[preL]] - sz[st[preL]] + 1, -1);
    preL++;
  }
  ans = max(r - preL + 1, ans);
  add(tl + 1, 1), add(tr + 1, -1);
  for (int &v : e[x])
    if (v != fa) las_dfs(v, x, preL, r + 1);
  add(tl + 1, -1), add(tr + 1, 1);
  while (preL > l) {
    preL--;
    add(dfn[st[preL]] + 1, -1), add(dfn[st[preL]] - sz[st[preL]] + 1, 1);
  }
}
 
inline void solve() {
  read(n), ans = 1, totdfn = top = 0;
  e.assign(n + 2, vector<int>());
  fe.assign(n + 2, vector<int>());
  // for (int i = 0; i <= n; i++) f1[i] = f2[i] = 0;
  for (int i = 1, x, y; i < n; i++) read(x, y), e[x].emp(y), e[y].emp(x);
  for (int i = 1, x, y; i < n; i++) read(x, y), fe[x].emp(y), fe[y].emp(x);
  pre_dfs(1, 0);
  las_dfs(1, 0, 1, 1);
  printf("%d\n", ans);
}

View Code

133: OR 【二进制性质： a+b == a|b + a&b】

关于这样是如何保证 \( 0 <= a_{i} <= C_{i} 以及 C_{i} < B_{i} \) 的

先说第一种：\( 0 <= a_{i} <= C_{i} \) → \( C_{i} - B_{i} == a_{i}\) & \(a_{i-1} \)

①显然我们枚举0~32位bit，并没有考虑最高位，所以全是正数。

② \( a_{i} \) 不会超过某一个范围，这与 \( B_{i} , C_{i}-B_{i} \) 有关，比如说我们考虑32位是1，显然这个时候 \( B_{1} ， C_{1} - B_{1} \) 在这一位都是0，但是我们设置第一位是1，不符合，可以直接 \( return 0; \) 的！！！

再说第二种： \( C_{i} < B_{i} \)

我们知道 \( a+b >= a|b \) 的，那么就要求数据 \( C_{i} >= B_{i} \) ，所以如果出现上诉情况，直接puts(0)是对的，但是为甚恶魔不特判也是可以的呢？

假设 \( C_{i} - B_{i} == -1 \) ，（-1的任意一位都是1）那么我们枚举到这一位的时候，有 \( B_{i} == 0 ,C_{i} - B_{i} == 1 \) 这明显是矛盾的，不管我们的 v 是1或者是0，都会直接在 OK函数里 \( return 0 \) .

ll n, m, b[maxn], c[maxn], ans;

inline int OK(ll x, int v) {
  for (int i = 1; i < n; i++) {
    if (((b[i] & x) == 0 && v) || ((c[i] & x) && !v)) return 0;
    // if ((c[i] & x) && (b[i] & x) == 0) return 0; // 可加可不加
    if (v){
      if((c[i]&x))v = 1;
      else v = 0;
    }
    else {
      if((b[i]&x))v = 1;
      else v = 0;
    }
  }
  return 1;
}

inline void solve() {
  read(n), ans = 1;
  for (int i = 1; i < n; i++) read(b[i]);
  for (int i = 1; i < n; i++) {
    read(c[i]), c[i] -= b[i];
    // if (c[i] < 0) { // 可加可不加
    //   puts("0");
    //   return;
    // }
  }
  for (int i = 0; i <= 32; i++) 
    ans *= (OK(1ll << i, 1) + OK(1ll << i, 0));
  printf("%lld\n", ans);
}

View Code

134 : a simple problem with integers hdu【根据mod维护树状数组】

此题要求实现对\( [ l , r ] \) 区间内，对满足 \( ( i - l ) mod k == 0 \) 的数加上数字 x ，然后还要支持单点查询。

由于此题的特殊性，我们不打算直接将数组a插入到树状数组里面，而是打算利用树状数组维护权值的变化！

由于此题进行的区间操作是不连续的，而是带一定规律的，所以我们必须根据规律维护权值变化，因此不能单纯把数组a插入到树状数组里面，同时考虑根据这个规律维护权值的变化。

怎么维护呢？不难发现，我们只需要建10*10个树状数组，那么 \( sum(i, k) \)就表示在模数为\( k \)，余数为 \( j \) 时前缀 \( 1 到 i \)的权值变化前缀和！

10*10个树状数组中，每个数组维护 \( k，j \) 条件下的值，等到查询时，直接暴力枚举模数k即可，而i是询问给定的，所以复杂度是 \( O(10*logn) \)，整体还是很快的。

后记：此题维护权值变化并不是通过以防的区间赋值来实现，而是像差分数组一样利用树状数组，便实现当查询单个数权值变化的功能！

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 5e4 + 3, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-8;

int n, m, tr[maxn][11][11], a[maxn];

inline void add(int x, int m, int k, int v) {
  while (x <= n) {
    tr[x][k][m] += v;
    x += lowbit(x);
  }
}

inline ll sum(int x) {
  ll res = 0, id = x;
  while (x > 0) {
    for (int i = 1; i <= 10; i++) res += tr[x][i][id % i];
    x -= lowbit(x);
  }
  return res;
}

inline void solve() {
  me(tr, 0);
  for (int i = 1; i <= n; i++) read(a[i]);
  read(m);
  while (m--) {
    int op, l, r, k, x;
    read(op);
    if (op == 1) {
      read(l, r, k, x);
      add(l, l % k, k, x);
      // add(l + ((r - l) / k) * k + k, l % k, k, -x); 
      // 这个表明要消除对 r之后（i-l）%k==0数的影响
      add(r + 1, l % k, k, -x); // 但是实际上这个也是对的！！！
    } else {
      read(x);
      printf("%lld\n", a[x] + sum(x));
    }
  }
}

int main() {
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  // read(TEST);
  while (~scanf("%d", &n)) solve();
}

View Code

135:B-发糖啦!!_牛客2021年七夕节比赛【暴力枚举所有约数】

虽然这个题 \( TEST<=1e4 且 n <= 1e9 \)，但是先欧拉筛筛一遍素数是 \( O(\sqrt{n}) \)的，然后筛取所有质因子也是 \( O(\sqrt{n}) \)的，那么这样的话，已经是5e8左右的复杂度了，但在牛客神机面前不算什么问题，然后重点在于如何不重不漏地枚举出所有的约数。

//#pragma GCC optimize(3, "inline", "-Ofast")
#include <bits/stdc++.h>

#include <ext/pb_ds/priority_queue.hpp>
#define lowbit(x) (x & (-x))  //-为按位取反再加1
#define mseg ((l + r) >> 1)
#define ls (ro << 1)
#define rs ((ro << 1) | 1)
#define ll long long
#define lld long double
#define uint unsigned int
#define ull unsigned long long
#define fi first
#define se second
#define pln puts("")
#define ios_fast ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define deline cout << "-----------------------------------------" << endl
#define de(a) cout << #a << " = " << a << endl
#define de2(a, b) de(a), de(b), deline
#define de3(a, b, c) de(a), de(b), de(c), deline
#define de4(a, b, c, d) de(a), de(b), de(c), de(d), deline
#define emp(a) push_back(a)
#define iter(c) __typeof((c).begin())
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define me(x, y) memset((x), (y), sizeof(x))
#define mp make_pair
using namespace std;
/////快读
template <typename T>
inline void read(T &res) {  //
  T x = 0, f = 1;
  char ch = getchar();
  while (ch != EOF && (ch < '0' || ch > '9')) {
    if (ch == '-') f = -1;
    ch = getchar();
  }
  while (ch != EOF && ch >= '0' && ch <= '9') {
    x = (x << 1) + (x << 3) + (ch ^ 48);
    ch = getchar();
  }
  res = x * f;
}
template <typename T, typename... Args>
inline void read(T &t, Args &...a) {
  read(t), read(a...);
}

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e5 + 3, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-8;

ll n, m, tot, ans, len, tn, timer;
PII p[maxn];
vector<ll> pr, ba;
int vis[maxn], cnt;

inline void initPrime() {
  for (int i = 2; i < maxn; i++) {
    if (!vis[i]) pr.emp(i);
    for (ll &j : pr) {
      if (maxn <= 1ll * i * j) break;
      vis[i * j] = 1;
      if (i % j == 0) break;
    }
  }
}

inline void getBase(int x, ll cur) {
  // timer++;
  if (x > tot) {
    if (cur > 1) ba.emp(cur);
    return;
  }
  for (int i = 0; i <= p[x].fi; i++) getBase(x + 1, cur), cur *= p[x].se;
}

void solve() {
  read(n), tn = n, tot = 0, ans = n, len = 1, timer = 0;
  ba.clear();
  for (ll &i : pr) {
    if (tn < 1ll * i * i) break;
    if (n % i == 0) {
      p[++tot] = mp(0, i);
      while (n % i == 0) n /= i, p[tot].fi++;
    }
  }
  if (n > 1) p[++tot] = mp(1, n);
  getBase(1, 1);
  // de2(timer,ba.size());
  for (ll &res : ba) {
    m = tn, cnt = 0;
    while (m % res == 0) cnt++, m /= res;
    if (m >= res) continue;
    if (cnt > len)
      ans = res, len = cnt;
    else if (cnt == len && res < ans)
      ans = res;
  }
  printf("%lld\n", ans);
}

int main() {
  initPrime();
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  read(TEST);
  while (TEST--) solve();
}

View Code

136:UVA10140 Prime Distance 【埃氏筛】

埃氏筛虽然不及欧拉筛快，但是可迁移性十分高，许多暴力可以使用埃氏筛的思路来优化，特别是有关于因子、乘法等等的问题。

又好比这一题：【2021暑假牛客多校： xay love count】

关于这题埃氏筛，我们先预处理出 \( O(\sqrt{1e9}) \) 的质数，然后拿这些质数在 \( [ l , r ] \) 区间做埃氏筛，这样子可以在 \( sq = \sqrt{n} ， O(sq*log(sq)) \) 的时间内算出来，特判一下区间内质数是否0个或者1个即可。

137：Nearest Beautiful Number【CF DIV3】

由于要求最小，我们考虑枚举 \( 0~i \) 保留多少位，然后剩下的问题就是：

从 \( num_{i+1至n} \)构造一个数，使得这个数大于等于原来的 \( s_{i+1至n} \) ，然后就是贪心DFS即可，如果前面已经有一个位num[x]大于s[x]，那么后面从0枚举，否则从 \( s[x]-‘0’ \)枚举，总的复杂度在 \( O(n^{2}) \) 左右，但是由于 \( n<10 \)，所以可以直接算出来，十分快

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 1e6 + 3, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-12;

string s, ans;
int cnt[20][maxn], has[20], k;

inline void init() {
  me(cnt, 0);
  for (int i = 0; i < s.size(); i++) {
    cnt[s[i] - '0'][i]++;
    for (int j = 0; j < 11; j++) cnt[j][i + 1] += cnt[j][i];
  }
}

inline int get(int x) {
  if (x < 0) return 0;
  int res = 0;
  for (int i = 0; i < 11; i++) res += (cnt[i][x] > 0);
  return res;
}

inline int DFS(int x, int e, int tag, int lef) {
  if (lef < 0) return false;
  if (x == e) return ans >= s;
  int be = tag ? 0 : (s[x] - '0');
  for (int i = be; i <= 9; i++) {
    ans[x] = '0' + i;
    int t = (has[i] == 0);
    if (t) has[i]++;
    if (DFS(x + 1, e, tag | (ans[x] > s[x]), lef - t)) return true;
    if (t) has[i]--;
  }
  return false;
}

inline void solve() {
  cin >> s >> k, ans = s;
  init();
  for (int i = s.size(); ~i; i--) {
    if (get(i - 1) > k) continue;  // 注意，是i-1
    // ans = s; // 不需要
    for (int j = 0; j < 11; j++) has[j] = i ? cnt[j][i - 1] : 0;
    if (DFS(i, s.size(), 0, k - get(i - 1))) break;
  }
  cout << ans << endl;
}

View Code

138：Polycarp and String Transformation【cf div3】

又是这类删除某一字母的题目。设x为字符串字母的种数，那么这个串将会叠加x次，第一个删除的只会叠加1次，第二个叠加2次，第三个3次，以此类推。

那么这个字母按顺序出现的次数应该分别是1的倍数，2的倍数，3的倍数... 以此类推。

然后我们又发现，只需要倒序遍历一次，再reverse一下，就是字母删除的顺序。

所以我们只需要枚举1~n个位置，看看是否满足两个条件即可。

（1）所有字母出现的次数与自己删除的顺序相匹配

（2）同时出现的顺序不能掉乱【这个比较难写，所以直接暴力判断即可】

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 1e6 + 3, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-12;
 
string str, ans, ord;
int vis[129], tot[129];
 
inline int check() {
  me(vis, 0);
  string tmp;
  for (char& c : ord) {
    for (int i = 0; i < ans.size(); i++)
      if (!vis[ans[i]]) tmp.push_back(ans[i]);
    vis[c]++;
  }
  return tmp == str;
}
 
inline void solve() {
  cin >> str, me(tot, 0);
  ord.clear(), ans.clear();
  for (int i = str.size() - 1; ~i; i--) {
    if (!tot[str[i]]) ord.push_back(str[i]);
    tot[str[i]]++;
  }
  reverse(ord.begin(), ord.end());
  map<char, int> cnt;
  for (int i = 0; i < ord.size(); i++) {
    cnt[ord[i]] = tot[ord[i]] / (i + 1);
  }
  for (int i = 0; i < str.size(); i++) {
    ans.push_back(str[i]);
    cnt[str[i]]--;
    if (!cnt[str[i]]) cnt.erase(str[i]);
    if (cnt.empty() && check()) { // check是为了判断顺序
      cout << ans << " " << ord << endl;
      return;
    }
  }
  cout << -1 << endl;
}

View Code

同时还有这一道题：Black Box

题意：设x为一个二进制串，每次左移一位成为x₁，那么 \( y = x_{0} + x_{1} +...+x_{n-1} \)。现在给出y，让你求 x。

分析样例：1011 = 0101 + 1010 + 0100 + 1000

竖着看：\( 1 = 0 + 1 + 0 + 1 + carry_{2} \)

\( 0 = 1 + 0 + 1 + 0 + carry_{1} \)

\( 1 = 0 + 1 + 0 + 0 + carry_{0} \)

\( 1 = 1 + 0 + 0 + 0 + no-carry \)

就这么看，我们发现 \( y_{i} = x_{0} + x_{1} + ... + x{i} + carry_{i-1} \) ，所以直接累计1的个数同时维护一个进位即可。

int n;
char s[maxn], ans[maxn];

inline void solve() {
  read(n), scanf("%s", s + 1);
  int cnt = 0, carry = 0;
  for (int i = 1; i <= n; i++) {
    if (((cnt + carry) & 1) != (s[i] - '0')) {
      cnt++;
      ans[i] = '1';
    } else {
      ans[i] = '0';
    }
    carry = (carry + cnt) / 2;
  }
  ans[n + 1] = '\0';
  puts(ans + 1);
}

View Code

139：Dynamic Diameter 【线段树维护树的直径+支持边权修改】

呜呜呜，不得不说，洛谷第一篇题解真的牛：传送门

如果直接维护D数组，真的很难下手，所以考虑分别固定一下lca的位置，然后分治求最优解，真的巧妙

定义mx、mn为区间最值

定义lmx为当lca在左儿子区间时，所维护的： \( max( dis_{l} - 2*dis_{k} ) 其中 k > l \)

定义rmx为当lca在右儿子区间时，所维护的： \( max( dis_{r} - 2*dis_{k} ) 其中 k < r \)

定义D为L,R区间的节点形成的直径的最大值。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e5 + 3, maxe = 4e5 + 11, mod = 998244353;
const lld eps = 1e-12;

// 链式前向星
struct EDGE {
  int u, v;
  ll w;
  int nxt;
} e[maxe];
int totEDGE, head[maxn];

inline void addEdge(int x, int y, ll w) {
  e[++totEDGE] = {x, y, w, head[x]}, head[x] = totEDGE;
  e[++totEDGE] = {y, x, w, head[y]}, head[y] = totEDGE;
}

// 线段树变量
ll n, m, w, ans, dis[maxn], a[maxn * 2], mx[maxn << 2], mn[maxn << 2];
ll top, lmx[maxn << 2], rmx[maxn << 2], D[maxn << 2], lb[maxn], rb[maxn];
ll tag[maxn << 2];

inline void DFS(int x, int f) {
  a[++top] = x, lb[x] = top;
  for (int i = head[x]; i; i = e[i].nxt)
    if (e[i].v != f) {
      dis[e[i].v] = dis[x] + e[i].w;
      DFS(e[i].v, x);
      a[++top] = x;
    }
  rb[x] = top;
}

inline void modify(int ro, ll v) {
  mx[ro] += v, mn[ro] += v;  // d = disl+disr-2*disk，抵消了modify
  lmx[ro] -= v, rmx[ro] -= v, tag[ro] += v;
}

inline void push_up(int ro) {
  mx[ro] = max(mx[ls], mx[rs]), mn[ro] = min(mn[ls], mn[rs]);
  lmx[ro] = max({lmx[ls], lmx[rs], mx[ls] - 2 * mn[rs]});
  rmx[ro] = max({rmx[ls], rmx[rs], mx[rs] - 2 * mn[ls]});
  D[ro] = max({D[ls], D[rs], lmx[ls] + mx[rs], mx[ls] + rmx[rs]});
  return;
}

inline void push_down(int ro) {
  if (tag[ro]) modify(ls, tag[ro]), modify(rs, tag[ro]), tag[ro] = 0;
}

inline void build(int ro, int l, int r) {
  if (l == r) return modify(ro, dis[a[l]]), D[ro] = 0, void();
  build(ls, l, mseg), build(rs, mseg + 1, r);
  push_up(ro);
}

inline void update(int ro, int l, int r, int s, int e, ll v) {
  if (s <= l && r <= e) return modify(ro, v), void();
  push_down(ro);
  if (s <= mseg) update(ls, l, mseg, s, e, v);
  if (mseg < e) update(rs, mseg + 1, r, s, e, v);
  push_up(ro);
}

inline void solve() {
  read(n, m, w), me(head, 0), totEDGE = 0;
  for (ll i = 1, x, y, c; i < n; i++) read(x, y, c), addEdge(x, y, c);
  top = 0, DFS(1, 0);
  build(1, 1, top), ans = 0;
  while (m--) {
    ll id, v, a, b;
    read(id, v);
    id = (id + ans) % (n - 1);
    id++;
    v = (v + ans) % w;
    a = e[2 * id].u, b = e[2 * id].v;
    if (dis[a] < dis[b]) swap(a, b);
    update(1, 1, top, lb[a], rb[a], v - e[2 * id].w);
    e[2 * id - 1].w = e[2 * id].w = v;
    printf("%lld\n", ans = D[1]);
  }
}

View Code

140：力的平衡点【力的分解、模拟退火】

我们无法一下子求出答案，但是我们能一步一步逼近答案。

思路：首先我们随机一个初始点作为平衡点，如果他不平衡，那么力的向量就不能抵消，我们最后算出n个向量相加得到合力向量，然后我们使得这个点往合力的方向移动step的距离，注意，x移动的是cos*step，y移动的是sin*step。

随后，当step小于精度要求时，我们就求出了答案。

最后说一下，初始化step为1e5，算1000次左右，精度就降到1e-9了，所以总的复杂度不会超过 \( O(n^{2}) \) 。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e5 + 3, maxe = 4e5 + 11, mod = 998244353;
const lld eps = 1e-12, rate = 0.90; // rate = 0.95

int n, m, x[maxn], y[maxn], w[maxn];
double step, ansx, ansy;

#define sqr(x) (x) * (x)

inline void solve() {
  read(n), step = 1e5;
  for (int i = 1; i <= n; i++) read(x[i], y[i], w[i]);
  ansx = x[1], ansy = y[1];
  while (step >= eps) {
    double dis = 0, X = 0, Y = 0, tmp = 0;
    for (int i = 1; i <= n; i++) {
      tmp = sqrt(sqr(x[i] - ansx) + sqr(y[i] - ansy));
      if (tmp < eps) continue;  // 防止除0错误
      X += (x[i] - ansx) / tmp * w[i];
      Y += (y[i] - ansy) / tmp * w[i];
    }
    tmp = sqrt(X * X + Y * Y);
    if (tmp > eps) {
      ansx += step * X / tmp;
      ansy += step * Y / tmp;
    }
    step *= rate;
  }
  printf("%.3lf %.3lf\n", ansx, ansy);
}

View Code

141：F - Sports Betting【图论+概率论+集合】

题目要求赢家的期望。根据对赢家的定义，我们可以发现，赢家就是对应有向图里的强连通分量，即两者必然存在一条路径u->v,v->u。所以我们只需要枚举所有的强连通分量即可.

若令\( G(x,v) 代表x集合的边全部指向v集合的概率 \) ，令\( P \)为\( 强连通分量c \)的概率，则 \( P(c) * G(c,all \oplus c) \) 为该图存在的概率，然后令c为任意一个强连通分量，all为全集，有：

\( ans = \sum_{c \epsilon all} count(c) * P(c) * G(c,all \oplus c) \)

而 \( G(c,all \oplus c) \) 我们可以直接 \( O(n^2) \）计算，我们只需要保证c是强连通分量，然后c的边全部指向外边，而外边的边我们不需要管，因为无论正反向结果一样。

所以问题的关键就在怎么计算 \( P(c) \)。

我们考虑一个大的强连通分量是怎么构成的，好像十分困难，题解给出了一个反向的求解：

\( P(c) = 1 - P(c不是强连通分量) \)

那么c什么时候不是强连通分量呢？我们考虑枚举c的子集v，c不是强连通分量，当且仅当 v所有点都有边指向c的补集的，c的补集没有边指向v。所以我们枚举子集，然后直接得：

\( P(c) = 1 - \sum p(v) * G(v, c \oplus v) \)

最后暴力枚举累计答案。【预处理出in[i][j] = inv(a[i] + a[j])优化掉一个log】

ll n, m, a[20], all, p[maxn], in[20][20];

#define inv(x) (qpow(x, mod - 2) % mod)
inline ll qpow(ll x, ll y) {
  ll res = 1;
  while (y) {
    if (y & 1) res = (res * x) % mod;
    x = (x * x) % mod, y >>= 1;
  }
  return res;
}

inline ll G(int x, int v) {
  ll ret = 1;
  for (int i = 0; i < n; i++) {
    if ((1 << i) & x) {
      for (int j = 0; j < n; j++)
        if ((1 << j) & v) {
          ret = (ret * a[i] % mod * in[i][j]) % mod;
        }
    }
  }
  return ret;
}

inline ll DFS(int x) {
  if (p[x] != -1) return p[x];
  ll sigma = 0;
  for (int s = (x - 1) & x; s; s = (s - 1) & x)
    sigma = (sigma + DFS(s) * G(s, s ^ x)) % mod;
  return p[x] = ((1 - sigma) % mod + mod) % mod;
}

inline int count(int x) {
  int cnt = 0;
  while (x) x -= lowbit(x), cnt++;
  return cnt;
}

inline void solve() {
  read(n), all = (1 << n) - 1;
  for (int i = 0; i < n; i++) read(a[i]);
  for (int i = 0; i < n; i++)
    for (int j = 0; j < n; j++) in[i][j] = inv(a[i] + a[j]) % mod;
  me(p, -1), p[0] = 0, p[all] = DFS(all);
  ll ans = 0;
  for (int i = 1; i <= all; i++) {
    ans = (ans + count(i) * p[i] % mod * G(i, all ^ i) % mod) % mod;
  }
  printf("%lld\n", ans);
}

View Code

142：E. Equilibrium【判断区间内括号合法性+括号的最大深度】

给定a，b数组，每次操作选一个偶数长度的序列\( pos{ p_{1} , p_{2} \cdot , p_{k} } \) ，奇数位即 \( a_{p_{1}} ++ \) ，反之，b数组相应位置b++。

如果我们令 \( d_{i} = b_{i} - a_{i} \) ，那么就相当于奇数位让\( d_{p_{i}} -- \) ，偶数则++。

显然可以转化成括号序列，即\( d_{i} \)为正数则有 \( d_{i} \)个左括号，反之为右括号，那么此题就变成判断区间内括号合法性，然后输出括号最大深度（这个结论才是最妙的）

（1）合法性：只需要判断 \( [ l , r ] 区间内的最小值大于sum[l-1]，同时 sum[r] == sum[l-1] \)即可

（2）输出最大深度，求出\( [ l , r ] 区间内最大值 - sum[l-1]就是最大深度 \)

使用ST表查询最值可实现O（1）询问。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 1e5 + 3, maxe = 5e5 + 11, mod = 1e6;
const lld eps = 1e-4;
 
ll n, m, mn[maxn][22], mx[maxn][22], sum[maxn];
int a[maxn], b, lg2[maxn];
 
inline void initST() {
  me(mn, inf_ll), me(mx, -inf_ll), lg2[0] = lg2[1] = 0;
  for (int i = 2; i <= n; i++) lg2[i] = (lg2[i / 2] + 1);
  for (int i = 1; i <= n; i++) mx[i][0] = mn[i][0] = sum[i];
  for (int j = 1; j <= lg2[n]; j++) {
    for (int i = 1; i + (1 << j) - 1 <= n; i++) {
      mx[i][j] = max(mx[i][j - 1], mx[i + (1ll << (j - 1))][j - 1]);
      mn[i][j] = min(mn[i][j - 1], mn[i + (1ll << (j - 1))][j - 1]);
    }
  }
}
 
inline ll getMin(int l, int r) {
  int k = lg2[r - l + 1];
  return min(mn[l][k], mn[r - (1 << k) + 1][k]);
}
 
inline ll getMax(int l, int r) {
  int k = lg2[r - l + 1];
  return max(mx[l][k], mx[r - (1 << k) + 1][k]);
}
 
inline void solve() {
  read(n, m);
  for (int i = 1; i <= n; i++) read(a[i]);
  for (int i = 1; i <= n; i++) read(b), sum[i] = sum[i - 1] + b - a[i];
  initST();
  while (m--) {
    int l, r;
    read(l, r);
    if (getMin(l, r) < sum[l - 1] || sum[r] != sum[l - 1])
      puts("-1");
    else
      printf("%lld\n", getMax(l, r) - sum[l - 1]);
  }
}

View Code

143：最大独立集 / 最大团【模板】

namespace MaxClique {  // 最大团,如果需要求独立集需要reverse边
int N, g[maxn][maxn], cnt[maxn];  // cnt记录了第i个点往后的最大独立集
vector<int> ans, tmp;
inline int DFS(int x) {
  for (int i = x + 1, j; i <= N; i++) {
    if (cnt[i] + tmp.size() <= ans.size()) return false;
    if (g[x][i]) {
      for (j = 0; j < tmp.size(); j++)
        if (!g[i][tmp[j]]) break;
      if (j == tmp.size()) {
        tmp.emp(i);
        if (DFS(i)) return true;
        tmp.pop_back();
      }
    }
  }
  // 只能在这里返回，等到再也无法拓展独立集时就可以返回了
  if (tmp.size() > ans.size()) return ans = tmp, true;
  return false;
}
inline int getMaxClique() {
  me(cnt, 0), ans.clear();
  for (int i = N; i; i--) {
    tmp = vector<int>(1, i);
    DFS(i);
    cnt[i] = ans.size();
  }
  sort(ans.begin(), ans.end());
  return ans.size();
}
inline void initMaxClique(int n, int v) {  // v=0初始化最大团，v=1初始化独立集
  N = n;
  for (int i = 1; i <= n; i++)
    for (int j = 1; j <= n; j++) g[i][j] = v && (i != j);
}
};  // namespace MaxClique
using namespace MaxClique; // 模板n<=100只需10ms过

View Code

144：DInic求多重匹配【图论+逆向思维、枚举少量边来跑最大匹配（拓展问题基环树）】

该十字路口右转不影响其它方向，可以简化成为一个12条边、八个点的图。

我们考虑到只有四种情况是合法的：

也就是说，我们在这段时间内可以双倍利用该段时间，使得两个路口的车辆-1，这样想的话，答案就是：
\( ans = \sum_{八个路口i}a_{i} - maxMatch \)

但是这个图不是二分图，无法使用一般图多重匹配。

而且多出来的只有两条边，所以我们可以n方枚举这两条边的流量，然后跑最大匹配即可。【如图】

namespace maxFlow_dinic {
int N;
int dep[maxn], cur[maxn], S, T, head[maxn], top, VIS;
struct edge {
  int to, next;
  ll cap;
} e[maxn << 3];

inline void initDinic(int n, int s, int t) {  // 传入节点数量
  me(head, -1);
  top = 0, N = n, S = s, T = t;
}

inline void addEdge(int x, int y, ll cap) {
  e[top] = {y, head[x], cap}, head[x] = top++;
  e[top] = {x, head[y], 0}, head[y] = top++;
}

inline bool bfs() {
  for (int i = 1; i <= N; i++) dep[i] = 0, cur[i] = head[i];
  dep[S] = 1;
  queue<int> q;
  q.push(S);
  while (!q.empty()) {
    int x = q.front();
    q.pop();
    for (int i = head[x]; ~i; i = e[i].next) {
      int v = e[i].to;
      //注意dep数组的条件，是大于dep[x]+1就需要更新
      if (!dep[v] && e[i].cap > 0) {
        dep[v] = dep[x] + 1;
        q.push(v);
      }
    }
  }
  return dep[T] > 0;
}

inline ll dfs(int x, ll low) {
  if (!low) return 0;
  if (x == T) return VIS = true, low;
  ll used = 0, tmp = 0;
  for (int &i = cur[x]; ~i; i = e[i].next) {  //当前弧优化
    int v = e[i].to;
    if (dep[v] == dep[x] + 1 && e[i].cap > 0) {
      // min(low-used,e[i].cap);//流量的下界不能取错，保证不超额才行
      tmp = dfs(v, min(low - used, e[i].cap));
      if (tmp > 0) {
        used += tmp;
        e[i].cap -= tmp;
        e[i ^ 1].cap += tmp;
        if (used >= low) break;  // 此次DFS的流量已达上限，直接返回
      }
    }
  }
  if (!used) dep[x] = 0;
  return used;
}

ll Dinic() {
  ll maxFlow = 0;
  while (VIS = bfs()) {  // 赋值VIS
    while (VIS) {
      VIS = false;
      maxFlow += dfs(S, inf_ll);
    }
  }
  return maxFlow;
}
};  // namespace maxFlow_dinic
using namespace maxFlow_dinic;

vector<int> r = {0, 4, 5, 10, 15};
vector<int> t = {0, 2, 3, 7, 8, 9, 12, 13, 14};
int a[20];
inline int ID(int i, int j) { return (i - 1) * 4 + j; }

inline void solve() {
  for (int i = 1; i <= 4; i++) {
    for (int j = 1; j <= 4; j++) {
      read(a[ID(i, j)]);
    }
  }
  ll ans = 0, sum = 0;
  for (int i = 1; i <= 8; i++) sum += a[t[i]];
  for (int i = 0; i <= min(a[t[1]], a[t[8]]); i++) {
    for (int j = 0; j <= min(a[t[4]], a[t[6]]); j++) {
      initDinic(10, 9, 10);
      // 1
      addEdge(9, 1, a[t[1]] - i);
      addEdge(9, 3, a[t[3]]);
      addEdge(9, 5, a[t[5]]);
      addEdge(9, 8, a[t[8]] - i);
      // 2
      addEdge(1, 2, inf_int);
      addEdge(1, 6, inf_int);
      addEdge(5, 2, inf_int);
      addEdge(5, 6, inf_int);
      addEdge(5, 7, inf_int);
      addEdge(3, 2, inf_int);
      addEdge(3, 7, inf_int);
      addEdge(3, 4, inf_int);
      addEdge(8, 4, inf_int);
      addEdge(8, 7, inf_int);
      // 3
      addEdge(2, 10, a[t[2]]);
      addEdge(6, 10, a[t[6]] - j);
      addEdge(4, 10, a[t[4]] - j);
      addEdge(7, 10, a[t[7]]);
      ans = max(ans, i + j + Dinic());
    }
  }
  // de2(sum, ans);
  ans = sum - ans;
  for (int i = 1; i <= 4; i++) ans = max(ans, (ll)a[r[i]]);
  printf("%lld\n", ans);
}

View Code

145：White bird 【数学解方程 + 极限条件】

这道题如何枚举抛物线是一个难点，解方程也是一个难点。

（1）考虑已经合法，可以打到（x，y）的一条抛物线，同时这条抛物线上下都有许多矩形。此时我们改变抛物线的发射角度，调大或者调小。

①调小：这个时候我们原来合法的抛物线可能触碰到矩阵的左下角以及左上角

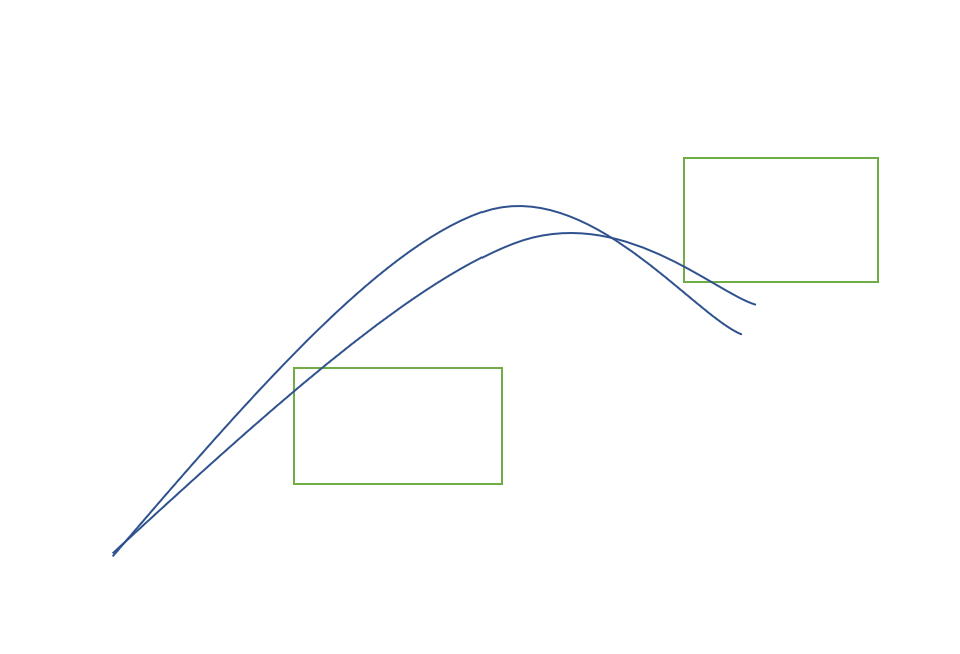
②调大：这个时候有可能碰到右下角以及右上角。

所以在极限条件下，我们枚举四个顶点，然后保证抛物线不会碰到其它线段即可。

然后就是解方程，我们得到（0，0）以及（\(x_{i}，y_{i} \)），解方程也不简单，但是实际上就是两个方程先平方，再相加消去三角函数求出 \( t^{2} \) ，因为 t 是正数，直接开方后求出两个解，然后小的t对应的是抛物线的左侧，大的t对应右侧，两个都试一试来求答案即可。【细节见代码】

struct Point {
  double x, y;
};

struct Line {
  double l, r, k;  // 对于竖边记录x，和上下y，横边则是y和左右x
} l1[maxn], l2[maxn];

vector<Point> p;
int n, V, ex, ey, t1, t2;
double g = 9.8;

inline double calc_y(double x, double vx, double vy) {
  return vy * (x / vx) - 0.5 * g * (x / vx) * (x / vx);
}

// 对方程两边平方，先求出T，再求出VX,VY
void getV(double x, double y, double &vx0, double &vy0, double &vx1, double &vy1) {
  double a = g * g / 4, b = (g * y - V * V), c = y * y + x * x;
  double d = b * b - 4 * a * c, t0, t1;
  if (d < 0 && d > -eps) d = 0;
  if (d < -eps) {
    vx0 = vx1 = vy0 = vy1 = -1;
    return;
  }
  double s = sqrt(d), t20 = (-b + s) / 2 / a, t21 = (-b - s) / 2 / a;
  // 其实因为T是时间，所以方程保证t20 > 0,t21 > 0
  if (t20 < eps) {
    vx0 = vy0 = -1;  // exit(-1)
  } else {
    t0 = sqrt(t20);
    vx0 = x / t0;
    vy0 = (y + 0.5 * g * t0 * t0) / t0;
  }
  if (t21 < eps) {
    vx1 = vy1 = -1;  // exit(-1)
  } else {
    t1 = sqrt(t21);
    vx1 = x / t1;
    vy1 = (y + 0.5 * g * t1 * t1) / t1;
  }
}

inline int OK(double x, double y) {
  double vx[2], vy[2];
  getV(x, y, vx[0], vy[0], vx[1], vy[1]);
  for (int i = 0, ans; i < 2; i++) {
    ans = true;
    if (vx[i] <= 0 || vy[i] <= 0) continue;  // 等号不能漏掉
    if (calc_y(ex, vx[i], vy[i]) < ey - eps) continue;
    for (int k = 1; k <= t1; k++) {  // 考虑横着的边
      double ly = calc_y(l1[k].l, vx[i], vy[i]);
      double ry = calc_y(l1[k].r, vx[i], vy[i]);
      if ((ly > l1[k].k) ^ (ry > l1[k].k)) ans = false;
    }
    for (int k = 1; k <= t2; k++) {  // 考虑竖着的边
      double ty = calc_y(l2[k].k, vx[i], vy[i]);
      if (l2[k].l < ty && l2[k].r > ty) ans = false;
    }
    if (ans) return true;
  }
  return false;
}

inline void solve() {
  read(n, V, ex, ey), t2 = t1 = 0;
  p.emp(Point({1.0 * ex, 1.0 * ey}));
  for (int i = 1; i <= n; i++) {
    double l, b, r, t;
    scanf("%lf%lf%lf%lf", &l, &b, &r, &t);
    if (l > ex) continue;  // 大于ex直接不需要
    r = min(r, 1.0 * ex);
    l1[++t1] = {l, r, b}, l1[++t1] = {l, r, t};  // 水平
    l2[++t2] = {b, t, l}, l2[++t2] = {b, t, r};  // 竖着
    p.emp(Point({l, t})), p.emp(Point({r, t}));
    p.emp(Point({l, b})), p.emp(Point({r, b}));
  }
  int ans = false;
  for (auto &tp : p) {
    ans |= OK(tp.x, tp.y);
    if (ans) break;
  }
  puts(ans ? "Yes" : "No");
}

View Code

146：F. Top-Notch Insertions 【组合 + 思维题 + 数据结构】

题目描述：给定一个序列，有m次操作，每次操作把第\( x_{i} \)个数插入到\( y_{i} \)处，保证x递增，而且插入的位置保证 \( a_{y_{i}} < a_{y_{i}+1} \)，即插入位置的后一位一定严格大于它，这样操作完成之后，序列是单调不减的。

我们模拟以下这个过程，例如样例三：

\( a_1,a_2,a_3,a_4,a_5\) 变成 \( a_4 , a_3, a_5 ,a_1,a_2 \)，我们发现，当下标不满足i<j时【比如\(a_4的下标大于a_3\)】，就会出现严格大于的现象。【记 c 为这个严格大于的次数】

利用组合数的思维来想，就是从n个数里面选n个，同时至少要有 c 种数出现，注意，这里不是重复组合，所求出的答案： \(ans = C^n_{2*n-c-1} \)。【这是edu的证明】

最后利用splay维护一下即可，我们维护的内容是：对于每一个坐标i，它前面一个数的坐标是否大于它。

比如说上述样例3，当\(a_3，a_4\) 插进去之后，\(a_1\)已经到第3位了，这个时候我们维护的集合里就有2，3两个数，因为这两个位置对答案有贡献，\( a_5\) 插入到 \(a_3\)之后，由于第3位已经在集合里了，所以这次对答案没影响，只需要对3加一，集合变成（2，4）即可。

最后splay有点细节，详细看代码

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 4e5 + 11, maxe = 4e5 + 11, mod = 998244353;
const lld eps = 1e-10;
 
// 功能 1：插入一个数
// 功能 2：为某一范围的数+1
// 功能 3：查询是否存在这个数
 
struct Splay {
  int tot, son[maxn][2], val[maxn], fa[maxn], root, tag[maxn];
  inline int newNode(int v) {
    ++tot, fa[tot] = tag[tot] = son[tot][0] = son[tot][1] = 0, val[tot] = v;
    return tot;
  }
  inline void init() {  // 初始化，添加左右哨兵
    tot = 0, root = newNode(-inf_int);
    son[root][1] = newNode(inf_int), fa[2] = root;
  }
  inline int chk(int x) { return son[fa[x]][1] == x; }
  inline void rotate(int x) {
    int y = fa[x], z = fa[y], k = chk(x), f = son[x][!k];
    if (z) son[z][chk(y)] = x;
    if (y) son[y][k] = f, fa[y] = x, son[x][!k] = y;
    if (f) fa[f] = y;
    fa[x] = z;
  }
  inline void add(int x, int v) {
    if (x) val[x] += v, tag[x] += v;
  }
  inline void push_down(int x) {
    if (tag[x]) add(son[x][0], tag[x]), add(son[x][1], tag[x]), tag[x] = 0;
  }
  inline void push_root(int x) {
    if (fa[x]) push_root(fa[x]);
    push_down(x);
  }
  inline void splay(int x, int par = 0) {
    push_root(x);
    while (x && fa[x] != par) {
      int y = fa[x], z = fa[y];
      if (z != par) rotate(chk(x) == chk(y) ? y : x);
      rotate(x);
    }
    if (!par && x) root = x;
  }
  inline void insert(int x) {
    int cur = root, par = 0;
    while (cur)  // 插入的数字不可能相同
      push_down(cur), par = cur, cur = son[cur][x > val[cur]];
    cur = newNode(x);
    if (par) fa[cur] = par, son[par][x > val[par]] = cur;
    splay(cur);
  }
  inline int count(int x) {
    int cur = root;
    while (cur && val[cur] != x) push_down(cur), cur = son[cur][x > val[cur]];
    return val[cur] == x;
  }
  // 为大于等于l的数+1
  inline void update(int l) {
    int cur = root, ro = val[root] < l ? root : -1; // 细节在这里，要判断第一个数是不是合法的
    while (cur && son[cur][l > val[cur]]) {
      push_down(cur), cur = son[cur][l > val[cur]];
      if (val[cur] < l) ro = cur; // 同时沿着路径记录！最大！的合法值
    }
    // if (ro == -1) ro = 1;
    splay(ro), splay(2, ro), add(son[2][0], 1), splay(son[2][0]);
  }
} splay;
 
namespace ACNumber {
ll fac[maxn], inv[maxn];
inline void initAC() {
  fac[0] = 1, inv[0] = 1, inv[1] = 1;
  for (int i = 2; i < maxn; i++)
    inv[i] = 1LL * (mod - mod / i) * (inv[mod % i]) % mod;
  for (int i = 1; i < maxn; i++) fac[i] = (fac[i - 1] * i) % mod;
  for (int i = 2; i < maxn; i++) inv[i] = (inv[i - 1] * inv[i]) % mod;
}
inline ll C(ll n, ll m) {
  if (m > n || n < 0 || m < 0) return 0;
  return fac[n] * inv[m] % mod * inv[n - m] % mod;
}
inline ll A(ll n, ll m) {
  if (m > n || n < 0 || m < 0) return 0;
  return fac[n] * inv[m] % mod;
}
};  // namespace ACNumber
using namespace ACNumber;
 
int n, m, ans;
 
inline void solve() {
  read(n, m), splay.init(), ans = 0;
  for (int i = 1, x, y; i <= m; i++) {
    read(x, y);
    if (!splay.count(y)) ans++, splay.insert(y);
    splay.update(y);
  }
  printf("%lld\n", C(2ll * n - ans - 1, n - ans - 1) % mod);
}

View Code

147：直径计数【n^3DP】

题目：给出n个点，求n个节点组成的所有可能的树的直径之和。

相类似的题目：无根树计数 (nowcoder.com)【此题要求的是无标号】

树的计数问题好难啊！！！

（1）无标号树的计数原理（组合计数，背包问题，隔板法，树的重心） - Flash_Hu - 博客园 (cnblogs.com)

（2）群论 - zhoukangyang - 博客园 (cnblogs.com)

（3）烷基计数（例题）：

\( O(n^3) \) DP ：定义f[i] 为 i 个节点的树有多少种，则:

\( = (i=j 或 i=k 或 j=k) C^{2}_{f_i+1} * f_k \)

\( f_n = (i!=j!=k) f_i * f_j * f_k \)

\( = (i==j==k) C^{3}_{f_i+2} \)

考虑 \( O(n^2) \) DP，我们定义 \( f_{i ，j} \)为有 i 个节点的树，而且根节点有 j 个儿子时的种类数。

这样做的好处是，我们可以累计贡献。

const ll inv2 = (mod + 1) / 2;
const ll inv6 = 166666668;  // (mod + 1) / 6

ll n, f[maxn][4];

inline ll C(ll x, int op) {
  if (op == 1) return x % mod;
  if (op == 2) return ((x + 1) * x % mod * inv2 % mod) % mod;
  return ((x + 2) * (x + 1) % mod * x % mod * inv6 % mod) % mod;
}

inline ll F(int x) { return (f[x][0] + f[x][1] + f[x][2] + f[x][3]) % mod; }

inline void solve() {
  read(n);
  f[1][0] = 1;
  for (int i = 1; i < n; i++) {
    for (int j = n; j > i; j--) {  // 一定要倒序DP，确保fn更新时，f[n-i*t]是未被i更新的
      for (int k = 1; k <= 3; k++) {
        for (int t = 1; t <= k && j - t * i > k - t; t++) {
          f[j][k] = (f[j][k] + C(F(i), t) * f[j - i * t][k - t] % mod) % mod;
        }
      }
    }
  }
  printf("%d\n", F(n));
}

View Code

148：K-段连续最大和【线段树 + 费用流思想】

每次取一个连续最大和，然后乘上-1，持续k次，具体证明使用了费用流（我也不懂，直接当模板了）。

维护最大最小连续和，然后乘上-1的时候swap这个SUM对象（包括s，l，r三个变量），然后每次求完k次累加就是答案。

最后记录一下rev的区间，结束之后清空一下就行。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 1e5 + 11, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-10;

struct SUM {
  int s, l, r;
  SUM operator+(const SUM &b) const { return {s + b.s, l, b.r}; }
  friend void swap(SUM &a, SUM &b) {
    swap(a.s, b.s), swap(a.l, b.l), swap(a.r, b.r);
  }
  friend SUM getMax(const SUM &a, const SUM &b) { return a.s > b.s ? a : b; }
  friend SUM getMin(const SUM &a, const SUM &b) { return a.s < b.s ? a : b; }
};

SUM cmx[maxn << 2], pmx[maxn << 2], smx[maxn << 2], am[maxn << 2];
SUM cmn[maxn << 2], pmn[maxn << 2], smn[maxn << 2];

struct Node {
  SUM cmx, pmx, smx, am;
};

int n, m, a[maxn], tag[maxn << 2];

inline void rev_val(int ro) {
  cmx[ro].s *= -1, cmn[ro].s *= -1;
  pmx[ro].s *= -1, pmn[ro].s *= -1;
  smx[ro].s *= -1, smn[ro].s *= -1;
  swap(cmx[ro], cmn[ro]), swap(pmx[ro], pmn[ro]);
  swap(smx[ro], smn[ro]), am[ro].s *= -1;
}

inline void push_up(int ro) {
  pmx[ro] = getMax(pmx[ls], am[ls] + pmx[rs]);
  smx[ro] = getMax(smx[rs], smx[ls] + am[rs]);
  cmx[ro] = getMax(getMax(cmx[ls], cmx[rs]), smx[ls] + pmx[rs]);
  pmn[ro] = getMin(pmn[ls], am[ls] + pmn[rs]);
  smn[ro] = getMin(smn[rs], smn[ls] + am[rs]);
  cmn[ro] = getMin(getMin(cmn[ls], cmn[rs]), smn[ls] + pmn[rs]);
  am[ro] = am[ls] + am[rs];
}

inline void push_down(int ro) {
  if (tag[ro]) {
    tag[ls] += (tag[ro] & 1), tag[rs] += (tag[ro] & 1);
    if (tag[ro] & 1) rev_val(ls), rev_val(rs);
    push_up(ro);
    tag[ro] = 0;
  }
}

inline void build(int ro, int l, int r) {
  tag[ro] = 0;
  if (l == r) {
    cmn[ro] = pmn[ro] = smn[ro] = am[ro] = cmx[ro] = pmx[ro] =
        smx[ro] = {a[l], l, r};
    return;
  }
  build(ls, l, mseg), build(rs, mseg + 1, r);
  push_up(ro);
}

inline void update(int ro, int l, int r, int x, int v) {
  if (l == r) {
    cmn[ro] = pmn[ro] = smn[ro] = am[ro] = cmx[ro] = pmx[ro] =
        smx[ro] = {v, l, r};
    return;
  }
  push_down(ro);
  x <= mseg ? update(ls, l, mseg, x, v) : update(rs, mseg + 1, r, x, v);
  push_up(ro);
}

inline void rev(int ro, int l, int r, int s, int e) {
  if (s <= l && r <= e) {
    tag[ro]++, rev_val(ro);
    return;
  }
  push_down(ro);
  if (s <= mseg) rev(ls, l, mseg, s, e);
  if (mseg < e) rev(rs, mseg + 1, r, s, e);
  push_up(ro);
}

inline Node merge(const Node &a, const Node &b) {
  return {getMax(getMax(a.cmx, b.cmx), a.smx + b.pmx),
          getMax(a.pmx, a.am + b.pmx), getMax(b.smx, a.smx + b.am),
          a.am + b.am};
}

inline Node query(int ro, int l, int r, int s, int e) {
  if (s <= l && r <= e) return {cmx[ro], pmx[ro], smx[ro], am[ro]};
  push_down(ro);
  if (s <= mseg && mseg < e)
    return merge(query(ls, l, mseg, s, e), query(rs, mseg + 1, r, s, e));
  if (s <= mseg) return query(ls, l, mseg, s, e);
  return query(rs, mseg + 1, r, s, e);
}

inline void solve() {
  read(n);
  for (int i = 1; i <= n; i++) read(a[i]);
  build(1, 1, n);
  read(m);
  while (m--) {
    int op, l, r, x;
    read(op, l, r);
    if (op == 0) {
      update(1, 1, n, l, r);
    } else {
      read(x);
      ll sum = 0;
      vector<PII> vec;
      while (x--) {
        Node res = query(1, 1, n, l, r);
        if (res.cmx.s <= 0) break;  // 小于等于0就可以退出
        rev(1, 1, n, res.cmx.l, res.cmx.r);
        sum += res.cmx.s;
        vec.emp(mp(res.cmx.l, res.cmx.r));
      }
      for (PII it : vec) rev(1, 1, n, it.fi, it.se);  // clear
      printf("%lld\n", sum);
    }
  }
}

View Code

149：同或 + 异或性质【贪心】

同或： \( 0(000) 同或 2(010) -> 5(101) = 0 ^ 2 ^ 7 \)

可以看出，同或可以转化成两次异或，而异或是具备交换律和结合律的，所以这道题就是先将n个数异或在一起，然后枚举\( 0 - n \)次异或 \( 2^k \) 即可。

int n, m;
__int128_t k, ans, cur, tmp;

inline void write(__int128_t a) {
  if (a >= 10) write(a / 10);
  putchar('0' + (a % 10));
}

inline void solve() {
  read(n, m), k = 1, k <<= m, k--;
  for (int i = 1; i <= n; i++) read(tmp), cur ^= tmp;
  for (int i = 0; i <= n; i++) ans = ans > cur ? ans : cur, cur ^= k;
  write(ans), pln;
}

View Code

150：树上两点的LCA+最大边权【kruskle裸题 / tarjan+带权并查集】

（1）直接kruskle + tarjan求lca，或者直接剖分求lca、倍增lca也行

（2）tarjan + 带权并查集！

考虑带权并查集的一个特点可以使用路径压缩：使用父节点来更新这个点的max权值，然后更新过之后就不会再更新了，而且我们知道原来的父节点已经被上面的节点更新，所以直接用fa更新自己。总的更新次数在O（n）。

最后注意一下tarjan：

①vis应该在中间被赋值为1

②我们查询到lca时，应该把询问交给lca，才能保证两个节点都是被更新的！！！

inline int Find(int x) {
  if (x == fa[x]) return x;
  int nxt = Find(fa[x]);
  mx[x] = max(mx[x], mx[fa[x]]);
  return fa[x] = nxt;
}
 
inline void initDSU() {
  for (int i = 1; i <= n; i++) vis[i] = 0, mx[i] = 0, fa[i] = i;
}
 
inline void tarjan(int x, int f) {
  for (auto [v, w] : e[x]) {
    if (f != v) {
      tarjan(v, x);
      fa[v] = x;
      mx[v] = max(1ll*mx[x], w);
    }
  }
  vis[x] = 1;
  for (int v : qry[x]) {
    if (vis[v]) {
      int lca = Find(v);
      b[lca].emp(mp(x, v));
    }
  }
  for (auto [l, r] : b[x]) {
    if(Find(l)!=Find(r))exit(-1);
    ans ^= max(mx[l], mx[r]);
  }
}

View Code

151 : 小体积、大价值背包【决策单调性优化DP】

你

152：Mentors【二叉树计数】

首先考虑一个子问题：去除题目的条件，不要求R为叶子节点，那么会有多少棵树满足要求？

定义 \( f_{i,j} 为考虑前i个节点，i个节点组成了j棵二叉树的个数 \)，那么我们现在考虑加入第 \( i \) 个节点，转移有三种：

初始 \( f_{i,j} = 0 \)。

①直接令 i 为孤儿（新建一棵只有一个节点的树），所以 \( f_{i,j} += f_{i-1j-1} \)

②把一棵树挂在 i 的任意一个儿子，树数量不变，（不需要乘个2，因为只有一个儿子就没有左右了）所以 \( f_{i,j} += j * f_{i-1,j} \) 。【乘 j 是因为要从 j 中选 1 棵】

③把两棵树挂在 i 的两个儿子，树的数量减少1棵（题目不考虑左右），所以 \( f_{i,j} += C^2_{j+1} * f_{i-1,j+1} \)

这样 \( f_{n,1} 就是答案 \)。

题目要求 R 为叶子节点，根据上面的转移来看，②③转移都会让 R 有儿子，所以我们限制一下转移就行。

但是题解好像说的是什么摆荡序列？抖动序列？【地精部落】。。

int n, R, P, f[2][maxn];
 
inline void solve() {
  read(R, n, P);
  int c = 1;
  f[0][1] = 1;
  for (int i = 2; i <= n; i++, c ^= 1) {
    for (int j = 1; j <= n; j++) {
      f[c][j] = f[c ^ 1][j - 1] % P;
      if (i == R) continue; // 限制后面的转移
      f[c][j] = (f[c][j] + 1ll * j * f[c ^ 1][j] % P) % P;
      f[c][j] = (f[c][j] + 1ll * (j + 1) * j / 2 % P * f[c ^ 1][j + 1] % P) % P;
    }
  }
  printf("%d\n", f[c ^ 1][1]);
}

View Code

153：Emails 【思维题？还是签到题？图的直径？还是去逼近图的直径？】

读题发现，就是给你一个图，第 i 天距离为 \( d^i \) 的两个节点会连上一条边，一开始第 0 天，距离为1的节点都有一条边。

那么在第几天这个图变成完全图？输出days或者days+1都可以。

一开始没有看出这个提示，完全不知道days+1是为什么。。。看了题解才发现，原来就是一个[读题]题。

首先不考虑题目给出的误差±1，那么答案很显然就是求出图上最远的两个点的距离D，然后输出 \( log_2(D) \)。

但是求图的直径的算法（还没看到有高效的）我不会，看了题解视频，出题人也说是 \( O(n*m) \) 的，显然不对。

然后考虑一些Tricks，设 node 为图最中心的节点，也就是说它到任意一个节点的最短路最小，设 \( D_{node} \) 为它最长的简单路长度。

Trick： \( D_{node} ≤ Diameter_{graph} ≤ 2 * D_{node} \)

转换为 \( Diameter_{graph} ≤ 2 * D_{node} ≤ 2 * Diameter_{graph} \)

再log2运算： \( log_2(Diamter_{graph}) ≤ log_2(D_{node}) + 1 ≤ log_2(Diameter_{graph}) + 1 \)

所以找任意一个节点，BFS求出最长的路径，直接输出 \( log_2(D) \)就行

154：B：Bricks 【思维 + DP】

题解

这个DP的状态转移并不是很直观，很难理解。

寄，想了半天都还是不理解。

ll g[maxn], n, m, s[maxn];

inline void solve() {
  read(n, m), g[0] = 1, n++;  // n++是最后一位是空巷子
  for (int x, i = 1; i <= m; i++) read(x), s[x]++;
  for (int i = 1; i <= n; i++) s[i] += s[i - 1];
  for (int i = 1; i <= n; i++)
    if (s[i] == s[i - 1] && (i - 1 - s[i] >= 0))
      g[i - s[i]] = (g[i - s[i]] + g[i - s[i] - 1]) % mod;
  printf("%lld\n", g[n - s[n] - 1]);
}

View Code

155：J：Cunning friends 【思维 + 博弈论】

156：Tree Projection【拓扑序 + dfs序 +构造】

一种解释：【树】2020ICPC小米网赛1G-Tree Projection – G@rage (luobotou.org)

首先，题目给出的两个序列对应的是同一棵树，但是并不同根，所以我们不能同时根据两个序列来考虑父子关系。

条件一：如果仅仅是给出一个，那么我们对于第i个节点，随机选取1~i-1作为父节点都是可以的，但是要求i节点与1~i-1之间不能超过两条边，否则就会成环了（因为不管是在拓扑排序还是dfs序，在前面的节点一定比后面的节点先遍历），所以每个节点only和1~i-1中的一个节点相连。

比如：

a = 1 2 4 3

b = 4 3 2 1 ，如果选了3-4，2-3，那么先遍历2，再遍历3，再遍历4，显然是不符合拓扑排序的，如果要符合，就会形成一个环

条件二：这个条件是针对dfs序来说的。

对于dfs序，一个节点如果是叶子节点，那么后续的节点就不会与它有边，但是如果没有边的这个条件对拓扑排序不成立，那么这样就不合法。

比如说：

a = 3 1 2 4

b = 1 2 3 4，显然根据拓扑序得到：1-3之间必须存在一条边，所以2必须是叶子节点，而且在拓扑排序中2-4这条边不应存在！

题解结论的证明：

反正一种贪心的思路，对于dfs序，从1~i-1里选一个作为父节点，那么肯定选择最前的作为父节点才最优（如果都后于自己，那么这种现象理解为该节点是树内部的节点，至少存在两个分支）。

（好难理解啊。。。由于这样构造一定有解，所以YES）

int n, p[maxn], a, b;

inline void solve() {
  read(n);
  for (int i = 1; i <= n; i++) read(a), p[a] = i;
  int cur;
  read(cur);
  puts("YES");
  for (int i = 2; i <= n; i++) {
    read(a);
    printf("%d %d\n", a, cur);
    if (p[cur] > p[a]) cur = a;
  }
}

View Code

157：E：Looping playlist 【环DP + 思维】

题目大概意思就是：

每首歌都有且只有一个主调，而且一个主调有七个音节{0, 2, 4, 5, 7, 9 , 11 and 12 half-steps,}，这些音节出现的顺序不需要相邻，比如说样例一：所有的音节都是出自Do开始的主调（即题目给出的表格的第一行）。【理解为一首歌是一个序列的一个子区间，这个区间内的所有数都必须存在于一个相同的集合中，题目的表格给出了12个这样的集合。】

这个题难点在于：它是一个环，如何控制长度小于等于n，以及如何维护最少歌曲数（即区间数）。

158：Meeting Bahosain【数论 + 方程组是否存在解】

首先来一手差分是很明显的，问题转化为b数组能否凑出a的差分数组各个值。

由ax+by=gcd(a,b)一定有解，设g为b1,b2...bn的最小公倍数，只要a[i]-a[j]是g的整倍数，一定有解。【十分好用的结论】

159： Card Game【概率论 + 思维】

160：Longest path problem【最小化最长路 ---- 最小化直径】

树的直径的一道好题

这个题目推出了结论：子树的直径的端点仍然在原树直径的端点处，所以选择从root向下枚举直径的中点！这样可以保证答案正确，且容易写。

还有逻辑很重要，0代表左边的子树信息，1代表右边的子树信息。

// #pragma GCC optimize(3, "inline", "Ofast")
#include <bits/stdc++.h>
#define lowbit(x) (x & (-x))  //-为按位取反再加1
#define re register
#define mseg ((l + r) >> 1)
#define ls (ro << 1)
#define rs ((ro << 1) | 1)
#define ll long long
#define lld long double
#define uint unsigned int
#define ull unsigned long long
#define fi first
#define se second
#define pln puts("")
#define dbg(a...) fprintf(stderr, a)
#define deline cout << "-----------------------------------------" << endl
#define de(a) cout << #a << " = " << a << endl
#define de2(a, b) de(a), de(b), deline
#define de3(a, b, c) de(a), de(b), de(c), deline
#define de4(a, b, c, d) de(a), de(b), de(c), de(d), deline
#define emp(a) push_back(a)
#define iter(c) __typeof((c).begin())
#define ios_fast ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define me(x, y) memset((x), (y), sizeof(x))
#define mp make_pair
using namespace std;
/////快读
template <typename T>
inline void read(T &res) {  //
  T x = 0, f = 1;
  char ch = getchar();
  while (ch != EOF && (ch < '0' || ch > '9')) {
    if (ch == '-') f = -1;
    ch = getchar();
  }
  while (ch != EOF && ch >= '0' && ch <= '9') {
    x = (x << 1) + (x << 3) + (ch ^ 48);
    ch = getchar();
  }
  res = x * f;
}
template <typename T, typename... Args>
inline void read(T &t, Args &...a) {
  read(t), read(a...);
}

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 3e5 + 11, maxe = 300 * 300 + 3, mod = 1e9 + 7;
const lld eps = 1e-10;

struct EDGE { 
  int to, nxt, w, id;
} e[maxn << 2];

struct Node {
  // d 为这个节点到一个端点的距离
  // eid 记录直径的边
  ll d, eid;
} tr[2][maxn];

ll n, m, ans[maxn], m1[2][maxn], m2[2][maxn], dp[2][maxn], top, dia;
int head[maxn];

/**
 * 这道题做题关键：
 * 我们发现移掉之后使得答案更小的边一定只出现在直径上，而且直径数量多于1就不需要DP了
 * 只考虑存在1条直径的情况，我们需要枚举直径上的每一条边，然后删掉他，这个时候我们就需要
 * 维护出左右两个子树的直径以及直径的中点，至于为什么是中点呢？
 * 因为直径的中点到树上任意一点的距离最大值最小：min({ max(dis[u][v]) })
 * 
 * 子问题一：如何维护左右两棵子树的直径。
 * 给出性质：
 * （1）子树的直径的一个端点 是 原树直径的一个端点，所以子树直径有一段是属于原树直径的，而且
 *    子树直径的中点一定在原树的直径上
 * （2）根据结论1，我们可以想到：已经知道各个节点 到 直径端点root的距离，那么该子树的直径就是
 *    最大的dis[x][root]。
 * 为什么呢？因为一定会有一段在原直径上，端点重合，所以只需要求出到root的dis即可
 * 这样我们就维护好 【 两个端点所在子树 】 的直径了
 * 这里的两个端点所在指： dp[0][x] 代表从x切开，子树root1的直径还剩多少
 * 那么相对的： dp[1][x] 代表从x切开，子树root2的直径还剩多少
 * 
 * 子问题二：如何维护直径的中点
 * 具体维护出那个点我还没细想，但是可以限制一下范围
 *    m1所标志的点代表 dis[x][root1] * 2 <= diameter
 *    m2所标志的点代表 dis[x][root2] * 2 > diameter 大概是这样的
 * 然后我们根据单调性可以双指针跑一遍
 * 
 * 最后再一次维护答案即可
 */

inline void addedge(int x, int y, int w, int id) {
  e[top] = {y, head[x], w, id}, head[x] = top++;
  e[top] = {x, head[y], w, id}, head[y] = top++;
}

inline PLL dfs(int x, int f, int t, ll cursum) { // dfs求出到根的距离
  tr[t][x] = {cursum, -1};
  PLL ret = mp(x, cursum);
  for (int i = head[x]; ~i; i = e[i].nxt) {
    int v = e[i].to;
    if (v == f) continue;
    PLL p = dfs(v, x, t, cursum + e[i].w);
    if (ret.se < p.se) ret = p, tr[t][x].eid = i;
  }
  return ret;
}

inline void DP(int x, int f, int t) {
  dp[t][x] = tr[t][x].d;  // 对root1做DP，应该维护的是dep_{x -> root2}的大小
  for (int i = head[x], v; ~i; i = e[i].nxt) {
    v = e[i].to;
    if (v == f) continue;
    DP(v, x, t);
    dp[t][x] = max(dp[t][v], dp[t][x]);
  }
}

inline void initMid(int root, int t) {
  int cur = root, mi = root, nxt, i, j, id, lasid = 0;
  ll cur_dia = 0;
  while (~tr[t][cur].eid) {
    i = tr[t][cur].eid;
    id = e[i].id;
    j = tr[t][mi].eid, nxt = j >= -1 ? e[j].to : 0;
    cur_dia = dp[t][cur];
    m1[t][id] = lasid ? m1[t][lasid] : cur;
    while (nxt && tr[t][mi].d * 2 < cur_dia) {
      m1[t][id] = mi, mi = nxt, j = tr[t][mi].eid;
      nxt = j > -1 ? e[j].to : 0;
    }
    m2[t][id] = mi;
    cur = e[i].to, lasid = id;
  }
}

inline void work(int root, int t) {
  int cur = root, i, nxt, id;
  while (~tr[t][cur].eid) {
    i = tr[t][cur].eid;
    nxt = e[i].to, id = e[i].id;
    int ml1 = m1[t][id];
    int ml2 = m2[t][id];
    int mr1 = m1[!t][id];
    int mr2 = m2[!t][id];
    ll L = max(tr[t][ml1].d, dp[t][cur] - tr[t][ml1].d);
    L = min(L, max(tr[t][ml2].d, dp[t][cur] - tr[t][ml2].d));
    ll R = max(tr[!t][mr1].d, dp[!t][nxt] - tr[!t][mr1].d);
    R = min(R, max(tr[!t][mr2].d, dp[!t][nxt] - tr[!t][mr2].d));
    ll tmp = max({dp[t][cur], dp[!t][nxt], L + R + e[i].w});
    ans[id] = tmp;
    cur = nxt;
  }
}

inline void solve() {
  read(n), me(head, -1);
  for (int i = 1, x, y, w; i < n; i++) read(x, y, w), addedge(x, y, w, i);
  int root1 = dfs(1, 0, 0, 0).fi, root2;
  PLL tmp = dfs(root1, 0, 0, 0);
  root2 = tmp.fi, dia = tmp.se;
  tmp = dfs(root2, 0, 1, 0);
  for (int i = 1; i < n; i++) ans[i] = dia;
  if (root1 == tmp.fi) {               // 必须要求只有一条直径
    DP(root1, 0, 1), DP(root2, 0, 0);  // 注意DP的顺序，求得数组调转了
    initMid(root1, 0), initMid(root2, 1);
    work(root1, 0);  //, work(root2, 1);
  }
  for (int i = 1; i < n; i++) printf("%lld\n", ans[i]);
}

int main() {
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  // read(TEST);
  while (TEST--) solve();
}

/*

 */

View Code

161：F. Points Movement 【线段树DP + 线段处理 + 思维】

这道题难点在于如何分配线段。

那不妨先考虑 DP[i][j] 表示第 i 个点向右跑到第 j 条线段的最小答案，那么很容易想到对于 dp[i][j] 就是从 \( dp[i-1][k] + F(k , j, i) \) 转移而来的，其中 F(k, j, i) 表示第 i 个点从 k 跑到 j 的最小答案, 这个很容易算。

所以直接上线段树维护 dp 数组，其中第 i 棵线段树表示 dp[i] 的所有信息，然后考虑滚动数组般滚动一下线段树数组就可以优化内存了。

我们需要维护两个值：(定义 a 为从 i + 1个节点跑到 j + 1条线段右端点的距离)

（1） dp[i][j] + 2 * a

（2） dp[i][j] + a

转移的时候呢，我们直接枚举第 i 个节点右边的 j 条线段，这样做是 \( O(n) \) 的，然后每一条线段考虑一下从（1）转移还是从（2）的最小值转移即可。

实现起来细节比较多，还要考虑到第 i 个点只左移，只右移的情况。

思路半清半楚写好能过真的感动死我了。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e5 + 11, maxe = 300 * 300 + 3, mod = 1e9 + 7;
const lld eps = 1e-10;
 
struct Segment_Tree {
  ll mn1[maxn << 2], mn2[maxn << 2];
  void push_up(int ro) {
    mn1[ro] = min(mn1[ls], mn1[rs]);
    mn2[ro] = min(mn2[ls], mn2[rs]);
  }
  void build(int ro, int l, int r, const ll f[], const ll b[]) {
    if (l == r) {
      mn1[ro] = f[l] + b[l];
      mn2[ro] = f[l] + 2 * b[l];
      return;
    }
    build(ls, l, mseg, f, b), build(rs, mseg + 1, r, f, b);
    push_up(ro);
  }
  ll query(int ro, int l, int r, int s, int e, int tp) {
    if (r < l || l > e || r < s || s > e) return inf_ll;
    if (s <= l && r <= e) return tp == 1 ? mn1[ro] : mn2[ro];
    return min(query(ls, l, mseg, s, e, tp), query(rs, mseg + 1, r, s, e, tp));
  }
} tr[2];
 
ll f[2][maxn], b[2][maxn];
int n, m, k, p[maxn], top;
PII s[maxn];
 
inline ll G(ll a, ll b) { return min(2 * a + b, 2 * b + a); }
 
inline void solve() {
  read(n, m), k = 0, top = 0;
  for (int i = 1; i <= n; i++)
    read(p[i]), f[0][i] = f[1][i] = b[0][i] = b[1][i] = 0;
  sort(p + 1, p + 1 + n);
  p[n + 1] = inf_int;
  for (int i = 1, x, y; i <= m; i++) {
    read(x, y);
    // 去掉覆盖的
    int L = lower_bound(p + 1, p + 2 + n, x) - p;
    int R = upper_bound(p + 1, p + 2 + n, y) - p;
    if (L == R) s[++k] = mp(x, y);
  }
  // 去掉包含的
  sort(s + 1, s + 1 + k, [&](PII a, PII b) {
    return (a.se < b.se) || (a.se == b.se && a.fi > b.fi);
  });
  for (int i = 1; i <= k; i++)
    if (!top || s[top].fi < s[i].fi) s[++top] = s[i];
  s[top + 1] = mp(inf_int, inf_int);
  // 计算出第一个合法的状态
  ll begin_status = p[1] > s[1].se ? p[1] - s[1].se : 0;
  int ptr = 1, cnt = 1;
  while (ptr <= top && s[ptr].fi < p[1]) ptr++;
  f[0][1] = begin_status, b[0][1] = p[2] - min(p[2], s[ptr].se);
  // de2(f[0][1], b[0][1]);
  while (ptr <= top && s[ptr].se < p[2]) {
    f[0][++cnt] = G(begin_status, s[ptr].fi - p[1]);
    b[0][cnt] = p[2] - min(p[2], s[ptr + 1].se);
    // de3(ptr, f[0][cnt], b[0][cnt]);
    ptr++;
  }
  // 计算后面n个节点
  int pre = 0, cur = 1, lasn = cnt, curn, L, R = ptr - 1;
  tr[pre].build(1, 1, cnt, f[0], b[0]);
  for (int i = 2; i <= n; i++, swap(pre, cur), swap(lasn, curn)) {
    curn = 0, L = R + 1;
    f[cur][++curn] = tr[pre].query(1, 1, lasn, 1, lasn, 1);  // 只选左边
    b[cur][curn] = p[i + 1] - min(p[i + 1], s[L].se);
    // de2(f[cur][1], b[cur][1]);
    while (R + 1 <= top && s[R + 1].se < p[i + 1]) R++;
    for (int j = L, k = lasn; j <= R; j++) {
      ll len = s[j].fi - p[i];
      while (k > 1 && b[pre][k - 1] < len) k--;
      ll tmp1 = tr[pre].query(1, 1, lasn, 1, lasn, 2);
      ll tmp2 = tr[pre].query(1, 1, lasn, 1, lasn, 1);
      f[cur][++curn] = min(tmp1 + len, tmp2 + 2 * len);
      b[cur][curn] = p[i + 1] - min(p[i + 1], s[j + 1].se);
      // de3(k, f[cur][curn], b[cur][curn]);
      // de2(tmp1, tmp2);
    }
    if (i < n) tr[cur].build(1, 1, curn, f[cur], b[cur]);
  }
  printf("%lld\n", f[pre][lasn]);
}

View Code

162：随机字符串生成器【概率论统计思想 + 精度较大的模拟】

看到这个问题，就想起之前的百度之星，之前的解决方法是先自己写一个数据生成器，然后统计一下数据的特征，然后根据特征求解问题。【一般的特征就是：出现次数，不动的数量等等，不同题目不同特征】

问题一：第二类字符串怎么生成？

这是一个带权随机，我们平时rand并没有做到带权，那应该怎么办呢？【不会写，寄了。。】

void gen2(){
    vector<LL>w(26,1);
    rep(i,1,L){
        LL sum=0;
        while(*min_element(w.begin(),w.end())>1)rep(i,0,25)w[i]>>=1;
        rep(i,0,25)sum+=w[i];
        LL tmp=rng()%sum+1;
        sum=0;
        int pos=-1;
        rep(j,0,25){
            sum+=w[j];
            if(sum>=tmp){
                pos=j;
                break;
            }
        }
        assert(pos!=-1);
        s[i]=pos+'a';
        rep(j,0,25)if(j!=pos)w[j]<<=1,assert(w[j]<=1e18);
    }
}

View Code

问题二：考虑直接分析，这两种数据应该有怎样的差异呢？

第一种不带权随机，每次出现的字母都是完全随机的，虽然理论上统计出来是一个均匀的分布，但是还是存在方差较大的可能。

第二种带权随机，每个字母出现后，出现的权值概率变小，所以下一个字母倾向于其它字母，这样随机出来的分布更加均匀，所以方差比上一种小很多

当然很多人用集合的极差也过了这道题，因为第二种比较均匀，所以出现最多的比出现最少的mx-mn<50左右。

问题三：如果我不会分析呢？我考虑直接计算两种字符串的概率，然后概率大的输出。

这样就出现了精度错误。概率的计算有两种运算，一种是乘法，另一种是每个字母的权值 ÷ 2。

乘法我们考虑使用log，这样乘上比较小的数就等于减去一个负数，而且这样保证精度正确。

每个字母的权值除法不能使用log，因为概率是 \( w_i / \sum w \) ，在分母处有加减，不能使用log运算。但是好在的是，由于随机输出，每个字母出现的次数不会多于100次，而每次÷2，最坏情况会增加一位精度，比如1÷2 = 0.5，但是除法做100次的话，精度最高也就 \( 10^{-100} \) ，这对有 \( -1.7e308 - 1.7e308 \) 范围的double来说是可以接受的，所以直接算就可以了。

当出现乘除很多的时候，而且还要比较大小，可以考虑一下log解决精度问题

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 1011, maxe = 300 * 300 + 3, mod = 1e9 + 7;
const lld eps = 1e-10;
 
lld First;
int n;
lld c[100];
char s[maxn];
 
inline lld Second() {
  lld tot = 26e18, ret = 0;
  for (int i = 0; i < 26; i++) c[i] = 1e18;
  for (int i = 1; i <= n; i++) {
    ret += log(c[s[i]-'a'] / tot);
    tot -= c[s[i]-'a'];
    c[s[i]-'a'] *= 0.5;
    tot += c[s[i]-'a'];
  }
  return ret;
}
 
inline void solve() {
  scanf("%s", s + 1);
  n = strlen(s + 1);
  puts(First > Second() ? "FIRST" : "SECOND");
}
 
int main() {
  for (int i = 1; i <= 1000; i++) First += log(1.0 / 26);
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  read(TEST);
  while (TEST--) solve();
}

View Code

163：条件概率|条件下的实际概率【概率论】

\( P(E_{i} |E_{tot}) = P(E_{i} E) / P(E) \)

其中\( P(E) \) 表示 r 个人买物品的概率，\( P(E_{i} E) \) 代表第 i 个人在 r 个人中买了物品的概率，

那么实际概率其实就是条件概率。

计算方式：枚举所有有 r 个1的二进制bitmask，对于第 i 位为1的概率，直接累加。最后所有合法概率加起来就是 \( P(E) \)。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 1011, maxe = 300 * 300 + 3, mod = 1e9 + 7;
const lld eps = 1e-10;

int n, m, kase;
double p0[30], p1[30], p2;

inline double DFS(int x, int cnt, double p) {
  if (x > n) {
    if (cnt == m) return p;
    return 0;
  }
  double t1 = 0, t2 = 0;
  t1 = DFS(x + 1, cnt + 1, p * p0[x]);
  // 计算出在m个人买了的条件下，第i个人买了的概率
  t2 = DFS(x + 1, cnt, p * (1 - p0[x]));
  p1[x] += t1;  // 加上合法概率
  return t1 + t2;
}

inline void solve() {
  for (int i = 1; i <= n; i++) scanf("%lf", &p0[i]), p1[i] = 0;
  p2 = DFS(1, 0, 1);
  printf("Case %d:\n", ++kase);
  for (int i = 1; i <= n; i++) printf("%.8lf\n", p1[i] / p2);
}

int main() {
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  // read(TEST);
  while (~scanf("%d%d", &n, &m) && n) solve();
}

View Code

164：小L与GCD【gcd的转化】

题解

（0）\( x|gcd \) 这种计数可以使用埃式筛进行计算，然后容斥一下，就可以计算出gcd = x的数量

很烦的是cnt数组直接爆60了(upd:nmd，超了20000，这玩个der)，导致num数组十分大，也爆了longlong，我使用题解的方法直接wa55%，longlong改成double直接TLE，寄了。

倒是很奇怪的是，暴力竟然跑得比正解快。

（1）按下标从小枚举字典序

错误的代码？为什么按二叉树的方式搜索不对？

inline void dfs(uint x, uint g, uint curid) {
  if (g == Gcd) ans += curid, k--;
  if (x >= p.size()) return;
  if (k > 0) dfs(x + 1, gcd(g, a[p[x]]), curid * p[x]);
  if (k > 0) dfs(x + 1, g, curid);
}

正确的代码：啊，为什么这个就是对的

inline void dfs(uint x, uint g, uint curid) {
  if (g == Gcd) ans += curid, k--;
  for (int i = x; i < p.size() && k; i++) // 每一次枚举下一位
    dfs(i + 1, gcd(g, a[p[i]]), curid * p[i]);
}

（2）使用迪利克雷因子层面的前缀和来优化埃式筛，使得复杂度降为: \( O(a * log(log(a))) \) 。

代码：（很烦啊这道题，但是枚举gcd是我没学过的？）

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e6 + 11, maxe = 1e7 + 3, mod = 1e9 + 7;
const lld eps = 1e-10;
 
vector<uint> p;
int vis[maxe], pr[maxe], top;
uint n, k, a[maxn], mx, Gcd;
uint s[maxe], ans;
double num[maxe];
ll cnt[maxe];
 
inline uint gcd(uint a, uint b) { return b ? gcd(b, a % b) : a; }
 
inline void initPrime(int mx) {
  for (int i = 2; i <= mx; i++) {
    if (!vis[i]) pr[++top] = i;
    for (int j = 1; j <= top; j++) {
      if (1ll * pr[j] * i > mx) break;
      vis[i * pr[j]] = 1;
      if (i % pr[j] == 0) break;
    }
  }
}
 
inline double qpow(double x, ll y) {
  double res = 1;
  while (y > 0) {
    if (y & 1) res *= x;
    x *= x, y >>= 1;
  }
  return res;
}
 
inline void dfs(uint x, uint g, uint curid) {
  if (g == Gcd) ans += curid, k--;
  for (int i = x; i < p.size() && k; i++)
    dfs(i + 1, gcd(g, a[p[i]]), curid * p[i]);
}
 
inline void solve() {
  read(n, k), mx = 0;
  if (n <= 30 && (1 << n) <= k) {
    puts("-1");
    return;
  }
  for (int i = 1; i <= n; i++) read(a[i]), mx = max(mx, a[i]);
  fill(s + 1, s + 1 + mx, 1);
  initPrime(mx);
  for (int i = 1; i <= n; i++) cnt[a[i]]++, s[a[i]] *= (i + 1);
 
  for (int i = 1; i <= top; i++)
    for (int j = mx / pr[i]; j; j--)
      s[j] *= s[j * pr[i]], cnt[j] += cnt[j * pr[i]];
  for (int i = 1; i <= mx; i++) s[i]--, num[i] = qpow(2, cnt[i]) - 1;
  for (int i = 1; i <= top; i++) {
    for (int j = 1; j <= mx / pr[i]; j++)
      s[j] -= s[j * pr[i]], num[j] -= num[j * pr[i]];
  }
 
  for (int i = mx; i && k; i--) {
    if (k >= num[i]) {
      ans += s[i], k -= num[i];
    } else if (num[i] > k) {
      Gcd = i;
      for (int j = 1; j <= n; j++)
        if (a[j] % i == 0) p.emp(j);
      dfs(0, 0, 1);
      break;
    }
  }
 
  if (k) {
    puts("-1");
  } else {
    printf("%u\n", ans);
  }
}

View Code

165：字典序练习【你真的会字典序吗？】

烦恼来源于2021XCPC网络赛,A题出题人把字典序与数值大小弄混淆了。

又学会了一种遍历树的方式，先跳入到子节点，如果答案不在这棵子树，直接跳到兄弟节点，而不需要一开始就知道所有子节点子树的大小

inline ll kth_number(ll n, ll k) {
  if (k > n) return -1;
  k--;  // 一开始就是1
  ll ans = 1;
  while (k > 0) {
    ll L = ans, R = ans + 1, sum = 0;
    // 计算出[合法]的子树节点数
    while (L <= n) sum += min(n + 1, R) - L, L *= 10, R *= 10; // 重点！
    if (sum > k) {  // 向下跳一层，跳到0号子节点
      ans *= 10, k--;
    } else {  // 向右移动，相当移到右边的兄弟节点
      ans++, k -= sum;
    }
  }
  return ans;
}

166：Paint【区间DP + 有限制的状态转移】

应该不难看出区间DP，定义\( dp[i][j][k] \) 为区间 \( [ i, j ] 的颜色为 k 的最少操作数 \)。

这样暴力转移就是\( O(n^4) \) ，寄了。

我们不难发现（贪心发现），如果 \( [ i , j ] 区间颜色涂成相同 \)，而且要求操作数最少，那么结束之后区间的颜色要么是 \( a[i] \)，要么是\( a[j] \) ，我们从后往前DP，从[i,j]区间枚举k来转移，如果\( a_i == a_k \)，那么我们就可以压缩一下[i,k]区间，使之变成一个点。

方程：\( dp_{i,j} = min( dp_{i+1,k-1} + 1 + dp_{k+1,j} ) \)

这样我们就可以降一维，变成 \( dp[i][j] \)，但是仍然是\( O(n^3) \)的。

然后题目说每个数出现次数不超过20，所以枚举出现的地方即可。\( O(20 * N^2) \)

这道题最重要的思路应该是找到相同颜色的点，然后先让这段区间同颜色（缩成一点），再去其它区间涂成相同颜色了吧

vector<int> a;
vector<vector<int>> dp, p;
int n;

inline void solve() {
  read(n);
  a.assign(n + 1, 0);
  dp.assign(n + 1, vector<int>(n + 1, inf_int));
  p.assign(n + 1, vector<int>());
  for (int i = 1; i <= n; i++) read(a[i]), p[a[i]].emp(i), dp[i][i] = 0;
  for (int i = n; i; i--) {
    for (int j = i + 1; j <= n; j++) {
      dp[i][j] = dp[i + 1][j] + (a[i] != a[i + 1]);  // 当[i,j]内没有颜色a[i]时
      for (const int &k : p[a[i]])
        // 为了保证转移的合法性（+1）,a[i + 1] != a[i] && a[k - 1] != a[i],
        // 可有可无,因为 +1 不会使答案变小
        if (k > i && k <= j && a[i + 1] != a[i] && a[k - 1] != a[i]) {
          int tmp = (i + 1 <= k - 1) ? dp[i + 1][k - 1] : 0;
          dp[i][j] = min(dp[i][j], dp[k][j] + tmp + 1);
          // 转移基于一个事实：
          // 如果dp[i+1][k-1]是最小的，那么这个区间相同的颜色应该是a[i+1]或a[k-1]
        }
    }
  }
  printf("%d\n", dp[1][n]);
}

View Code

这道题也可以证明一个结论：如果给区间涂色，在保证操作数最少的情况下，那么最终区间的颜色只能是a[L]或a[R]。

167：The Strongest Build 【优先队列维护搜索 + 记忆化】

暴力就可以了，但是一定要标记那些点是已经进过队列的！！！

考试的时候忘了记忆化，寄了。太久没写暴力BFS了。

168：Jumping Around 【构造】

题解

（1）c % 3 == 1时最难搞，需要分为 b == 3 / b > 3来构造

先用（3）中的方法2用完3*lim个3，剩下必定为： a-2 ， b ， 1。这个时候对b分类即可。

　　① b = 3时， 0 2 4 1 3 【恰好需要3个2，1个3，不消耗1】

　　 ② b = 4时， 0 2 4 1 3 5 【恰好需要4个2，1个3，不消耗1】

（2）c % 3 == 2时有1种方法使得恰好可以用完所有的3。

方法1：0 3 6 5 2 1 4 7 【消耗两个1，不消耗2】

（3）c % 3 == 0时有2种方法可以恰好用完所有的3。

方法1： 0 3 6 8 5 2 1 4 7 9 【消耗一个1，消耗两个2】

方法2： 0 3 6 7 4 1 2 5 8 【消耗两个1，不消耗2】

但是vj上提交wa了，会不会是因为没有spj呢？

  read(a, b, c);
  n = a + b + c;
  printf("0"), cur = 0;
  if (c % 3 == 1) { // 余1时
    int lim = c / 3;
    for (int i = 1; i <= lim; i++) cur += 3, c--, printf(" %d", cur);
    cur++, a--, printf(" %d", cur);
    for (int i = 1; i <= lim; i++) cur -= 3, c--, printf(" %d", cur);
    cur++, a--, printf(" %d", cur);
    for (int i = 1; i <= lim; i++) cur += 3, c--, printf(" %d", cur);
    if (b == 3) {
      while (a >= 1) cur++, a--, printf(" %d", cur);
      for (int i = 1; i <= 2; i++) cur += 2, b--, printf(" %d", cur);
      cur -= 3, c--, printf(" %d", cur);
      cur += 2, b--, printf(" %d", cur);
    } else if (b > 3) {
      for (int i = 1; i <= 2; i++) cur += 2, b--, printf(" %d", cur);
      cur -= 3, c--, printf(" %d", cur);
      for (int i = 1; i <= 2; i++) cur += 2, b--, printf(" %d", cur);
    }
  } else if (c % 3 == 2) { // 余2时
    int lim = c / 3;
    for (int i = 1; i <= lim + 1; i++) c--, cur += 3, printf(" %d", cur);
    cur--, a--;
    printf(" %d", cur);
    for (int i = 1; i <= lim; i++) c--, cur -= 3, printf(" %d", cur);
    cur--, a--;
    printf(" %d", cur);
    for (int i = 1; i <= lim + 1; i++) c--, cur += 3, printf(" %d", cur);
  } else { 
    int lim = c / 3;
    for (int i = 1; i <= lim; i++) c--, cur += 3, printf(" %d", cur);
    cur += 2, b--;
    printf(" %d", cur);
    for (int i = 1; i <= lim; i++) c--, cur -= 3, printf(" %d", cur);
    cur--, a--;
    printf(" %d", cur);
    for (int i = 1; i <= lim; i++) c--, cur += 3, printf(" %d", cur);
    cur += 2, b--;
    printf(" %d", cur);
  }
  while (a > 1) cur++, a--, printf(" %d", cur);
  int lim = (b + 1) / 2;
  for (int i = 1; i <= lim; i++) b--, cur += 2, printf(" %d", cur);
  if (cur == n) {
    cur--, a--, printf(" %d", cur);
  } else {
    cur++, a--, printf(" %d", cur);
  }
  while (b--) cur -= 2, printf(" %d", cur);
  pln;

View Code

169：videoGame probability【概率DP】

一开始读错题了，后面才发现只允许拿sum个items，然后累加概率之和。。。。这样就直接DP就行了【一开始以为拿sum个，然后求最大概率。。。】

但是如果求的是最大值的话，这样DP一下，最后输出最大值不也可以吗？【难道非要设dp[i][j]为前i个物品，用了j次的最大值？不要那么死板好不好】

int n, s[53], tot;
double p[53], dp[2511][maxn];
inline void solve() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> s[i] >> p[i];
  cin >> tot;
  dp[0][0] = 1;
  int cur = 0;
  // 题目要求【恰好】要到desired number的items
  // 所以也就是说，【累计】你获得sum个items的概率
  // 定义 dp[i][j]为当前获得i个items，用了j次的概率
  // 然后转移的话就是成功与失败两种转移
  // 最后累加概率
  for (int i = 1; i <= n; i++) {
    for (int j = cur + 1; j <= cur + s[i]; j++) {
      for (int k = j; k <= tot; k++) {
        dp[j][k] = dp[j - 1][k - 1] * p[i] + dp[j][k - 1] * (1 - p[i]);
      }
    }
    cur += s[i];
  }
  double ans = 0;
  for (int i = cur; i <= tot; i++) ans += dp[cur][i];
  cout << fixed << setprecision(3) << ans << endl;
}

170：Tour Route【哈密顿回路】

171：Multiples【数学 + 预处理优化】

背景：使用DFS+剪枝来容斥会TLE。

考虑继续减少枚举的集合数量来优化DFS。

考虑把质数集合分为两个：低位{2,3,5,7,11,13} ，高位{17,.....,127}。

如果能将两个集合分开独立计算，就可以实现减少集合枚举的数量。【meet in middle的思想】

但是应该怎么实现呢？这样做的合法性怎么证明？

比如我们枚举质数17的倍数，现在枚举到34，很显然，34=2*17，2这个因子是出现在低位集合的，而17出现在高位集合，所以34被枚举了两次，需要减去。

低位的容斥不会影响到高位，所以直接容斥计算出低位集合的贡献即可。但是高位集合倍数的枚举就不能出现k*p有{2,3,5,7,11,13}中的因子，这样我们就将高位集合和低位集合分开了，并且可以独立计算。

计算方法：

① 为了让枚举的倍数没有{2,3,5,7,11,13}中的因子，我们枚举k*p时【由于\( k*p<=b \)，所以\( b € [1 , b/p] \)】，k就不能有{2,3,5,7,11,13}中的因子，换句话说，k和{2,3,5,7,11,13}中的所有数都互质，实现的方法是\( gcd(k , \prod_{2,3,5,7,11,13}) == 1\)。　　

② 引入欧拉函数可积性的一个小结论: \(if\) \( i * j == 0\) \(then\) \(φ(i * j) == φ(i) * j \)

也就是说，互质的区间是可以右移len长度的【len为区间长度】。比如说：[1,6]中1，5与6互质，那么[1,6]右移6个单位，[7,12]还是有（1+6），（5+6）与6互质。

所以\( [1 , b/p ] \) 中与{2,3,5,7,11,13}互质的数的个数就是： k / len * (coprime[len]) + coprime[k % len] 。

#pragma GCC optimize("Ofast,unroll-loops")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4")
#pragma GCC target("popcnt,abm,mmx,avx")

#include <algorithm>
#include <cassert>
#include <cmath>
#include <functional>
#include <iomanip>
#include <iostream>
#include <map>
#include <numeric>
#include <queue>
#include <set>
#include <string>
#include <utility>
#include <vector>

using namespace std;
typedef long long ll;

const int MAXN = 128;
const int MAX = 513333;

ll maxi = 100000'00000'00000LL;
ll primos[] = {2,  3,  5,  7,   11,  13,  17,  19,  23, 29, 31,
               37, 41, 43, 47,  53,  59,  61,  67,  71, 73, 79,
               83, 89, 97, 101, 103, 107, 109, 113, 127};
ll maxlen = 31;
int cnt;
pair<int, ll> arr[MAXN];
pair<ll, int> grupos[31][MAX];
int sig[31];

void go(int pos, int len, ll prod, int lst, int added) {
  if (!added && lst >= 0) {
    grupos[lst][sig[lst]] = make_pair(prod, len);
    sig[lst]++;
  }
  if (pos == maxlen || prod * primos[pos] > maxi) {
    return;
  }
  go(pos + 1, len, prod, lst, 1);
  go(pos + 1, len + 1, prod * primos[pos], pos, 0);
}

int main() {
  ios_base::sync_with_stdio(0);
  cin.tie(0);
  int t;
  scanf("%d", &t);
  int from = 6;  // 调出来的，在6的时候比较优
  go(from, 0, 1, -1, 0);
  vector<int> small;
  int mxsz = 1;
  for (int i = 0; i < from; i++) {
    small.push_back(primos[i]);
    mxsz *= primos[i];
  }
  vector<int> coprime(mxsz + 1);
  for (int j = 0; j < t; j++) {
    ll res = 0;
    int a;
    ll b;
    scanf("%d%lld", &a, &b);
    int n = 0;
    while (n < small.size() && small[n] <= a) n++;
    for (int msk = 1; msk < (1 << n); msk++) {
      ll prod = 1;
      for (int j = 0; j < n; j++) {
        if (msk & (1 << j)) prod *= small[j];
      }
      int sgn = __builtin_popcount(msk) & 1;
      if (sgn)
        res += b / prod;
      else
        res -= b / prod;
    }
    cerr << res << endl;
    ll maxProd = 1;
    for (int i = 0; i < n; i++) maxProd *= small[i];
    coprime[0] = 0;
    for (ll i = 1; i <= maxProd; i++) {
      coprime[i] = __gcd(i, maxProd) == 1 ? coprime[i - 1] + 1 : coprime[i - 1];
    }
    for (int i = 0; i < 31; i++) {
      int primo = primos[i];
      if (primo > a) break;
      for (int k = 0; k < sig[i]; k++) {
        ll prod = grupos[i][k].first;
        int len = grupos[i][k].second;
        int sgn = (len & 1) ? 1 : -1;
        if (b < prod) continue;
        ll cant = b / prod;
        ll val = (cant / maxProd) * coprime[maxProd] + coprime[cant % maxProd];
        cerr << "val = " << val << " , " << cant << endl;
        res += sgn * val;
      }
    }

    printf("%lld\n", res);
  }
  return 0;
}

View Code

172：哈密顿回路【哈密顿通路 + 枚举起点】

！！！哈密顿通路的复杂度是 On 的，但是只适用于竞赛图，竞赛图就是两个节点之间都有一条边，这条边是有向边。

哈密顿图哈密顿回路哈密顿通路(Hamilton)_肘子的博客-CSDN博客_哈密顿回路

Hamilton 通路和回路的充分条件 - imbiansl’s space (gitee.io)

一个问题：为什么枚举所有的起点，然后从这个起点任选一条哈密顿通路就可以判定有没有环呢？难道不会出现刚刚好所有的终点都不指向起点吗？

任选这个词看起来很不靠谱，但是实际上不是任选的，每个竞赛图对应起点的哈密顿通路有且只有一条，所以1~n的不同起点的哈密顿通路是不同的，而且是唯一的，所以我们就可以枚举不同起点的哈密顿通路来找环了。

关于板子的解释：

每次枚举一个点，一开始把他作为Tail，然后从1枚举到n，试图把所有的点插入到路径里面，如果有边指向head，那么i直接在head插入，如果i不是指向head，而是head指向i，那么我们就要在nxt数组里找到最后一个指向i的点，和第一个i指向的点，然后更新nxt数组即可。

const int maxn = 1e3 + 11;

int n, g[maxn][maxn], nxt[maxn];

inline int Hamilton_Road(int s) {
  int head = s, tail = s;
  for (int i = 0; i <= n; i++) nxt[i] = -1;
  for (int i = 1; i <= n; i++) {
    if (i == s) continue;
    if (g[i][head]) {
      nxt[i] = head, head = i;
    } else {
      int x = head, y = nxt[head];
      while (~y && g[y][i]) x = y, y = nxt[y];
      nxt[x] = i, nxt[i] = y;
      if (y == -1) tail = i;  // 更新哈密顿通路的末尾
    }
  }
  nxt[tail] = head;  // 把哈密顿通路首尾相连，就是哈密顿回路
  return g[tail][head];
}

inline int OK() {
  for (int i = 1; i <= n; i++)
    if (Hamilton_Road(i)) return true;
  return false;
}

inline void solve() {
  for (int i = 1; i <= n; i++)
    for (int j = 1; j <= n; j++) g[i][j] = 0, cin >> g[i][j];
  if (n == 1) {
    cout << 1 << endl;
  } else if (!OK()) {
    cout << "-1" << endl;
  } else {
    int cur = 1;
    while (nxt[cur] != 1) {
      cout << nxt[cur] << " ";
      cur = nxt[cur];
    }
    cout << 1 << endl;
  }
}

int main() {
  int TEST = 1;
  while (cin >> n && n) solve();
}

View Code

172：竞赛图的判别【landau‘s 兰道定理】

兰道定理：link

一条边且度数计算为1的图只需要 ① \( \sum^{k}_{i=1} >= C^{2}_{k} \) ② \( \sum^{n}_{i=1} == C^{2}_{n} \) 就可以判别出是否是竞赛图

但是Football Game这题赢了会有2条边，打平相互连边，输了被连两条边，所以相当于建两个竞赛图，这样我们直接乘2就可以了【这个板子把C赋值为2就可以了】

const int maxn = 1e5 + 11;

int n, m, id[maxn], t[maxn];

inline int Landau() {
  ll sum = 0;
  for (int i = 1; i <= m; i++) {
    int x = id[i];
    sum += t[x];
    if (sum < (1ll * i * (i - 1))) return false;
  }
  return sum == 1ll * (m - 1) * m; // 计算的是2*C(n,2)
}

inline void solve() {
  while (n--) {
    cin >> m;
    iota(id + 1, id + 1 + m, 1);
    for (int i = 1; i <= m; i++) cin >> t[i]; 
    // 先按度数排好序
    sort(id + 1, id + 1 + m, [&](int i, int j) { return t[i] < t[j]; });
    cout << (Landau() ? "T" : "F") << endl;
  }
}

int main() {
  ios_fast;
  int TEST = 1;
  while (cin >> n && n) solve();
}

View Code

173：Spicy Restaurant【图论 - 多源BFS】

考虑到w的值只有1~100，所以暴力做100次BFS，每次都把w=（1~100）的节点入队，求出每个节点最短路径。

然后需要做最小值取min。最后就是O(1)回答询问了。【卡常，注意优化读入】

174：Hourly Coding Problem【二分 + 思维 + DP】

偷窥大佬的代码：LINK

175：阶乘分解【枚举质数 + 倍数】

考虑枚举质数，那么问题转换为单个质数的求解。

即：对于一个质数 p ，1*...*n中有多少个p？

对于 \( p^1 \) 而言，有 \( n / (p^1) \) 个。【枚举指数从1 ~ x 是一个好方法】

对\( p^2 \)而言，有\( n / (p^2) \) 个。以此类推，就可以求出 p 的贡献个数。

176：A simple Stone Game

177：2018牛客多校 Farm 【二维偏序 + 二维差分 + 思维】

upd：印象里一直记着这道题，但是发现好像有些误解，我一开始以为这种做法可以离线下来带时间戳的询问，但是今天回来看这道题，发现这里的query总是查询最后一个时刻的结果。。。【因为碰到了这道题，就直接把两道题的知识点混淆了：计数问题，这一题的话，应该是二维树状数组或者二维线段树吧，毕竟只有单点修改】

一 . 乍一看不会做（x 看题解。【似乎要转化为二维偏序问题还是有点难度的。】

① 考虑把所有不同编号的肥料和花朵都分开。

每一次浇 \( i \) 号肥料，就会在 (x1,y1) - (x2,y2) 这个矩阵内矩阵+1。

这样二维差分就能求出 \( (x,y) \) 这个位置被浇了多少次肥料。【记为 \( cnt_{x,y} \)】

二维差分： (x1,y1) ++ , (x1,y2+1)-- , (x2+1,y1)-- ,(x2+1,y2+1)++

考虑枚举1~n*m所有编号的肥料，然后对所有 i 号肥料做一次二维前缀和。【记为 \( sum_{x,y} \) 】

如果 \( sum_{x,y} == cnt_{x,y} \) 那么就说明（x，y）这个位置浇的肥料编号和花朵编号一致，存活数量+1。

② 每一次都做二维前缀和肯定会TLE，考虑优化。

我们考虑把矩阵的每一行分开考虑，在树状数组上做动态前缀和，然后加上一维时间来滚动，实现二维前缀和（不知道理解的对不对。。）

似乎这就是二维偏序问题，然后就可以算出来存活花朵的答案了，最后答案就是 n*m - ans。

#include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define lowbit(x) (x & (-x))
#define ll long long
#define ull unsigned ll
#define mp make_pair
#define me(a, b) memset(a, b, sizeof(a))
#define emp push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define fi first
#define se second
#define ls (ro << 1)
#define rs (ls | 1)
#define mseg ((l + r) >> 1)

const int maxn = 1e6 + 11, inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, mod = 998244353;

int n, m, k;
vector<vector<int>> sum;

struct Node {
  int x, y, w;
  bool operator<(const Node& rhs) const {
    if (x == rhs.x && y == rhs.y) return abs(w) > abs(rhs.w);
    if (x == rhs.x) return y < rhs.y;
    return x < rhs.x;
  }
};

vector<Node> q[maxn];

int tr[maxn], tg[maxn], Timer;

inline void add(int x, int v) {
  while (x <= m) {
    if (tg[x] != Timer) tg[x] = Timer, tr[x] = 0;
    tr[x] += v, x += lowbit(x);
  }
}

inline int get(int x) {
  int res = 0;
  while (x > 0) {
    if (tg[x] != Timer) tg[x] = Timer, tr[x] = 0;
    res += tr[x], x -= lowbit(x);
  }
  return res;
}

inline void solve() {
  cin >> n >> m >> k;
  sum.assign(n + 3, vector<int>(m + 3, 0));

  for (int a, i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++) cin >> a, q[a].push_back({i, j, 0});

  for (int lx, rx, ly, ry, w, i = 1; i <= k; i++) {
    cin >> lx >> ly >> rx >> ry >> w;
    q[w].push_back({lx, ly, 1});
    q[w].push_back({lx, ry + 1, -1});
    q[w].push_back({rx + 1, ly, -1});
    q[w].push_back({rx + 1, ry + 1, 1});
    sum[lx][ly]++, sum[rx + 1][ly]--, sum[lx][ry + 1]--, sum[rx + 1][ry + 1]++;
  }

  for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
      sum[i][j] += sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1];

  int ans = 0;
  Timer = 0;
  for (int i = 1; i <= n * m; i++) {
    sort(q[i].begin(), q[i].end());
    Timer++;
    for (auto [x, y, w] : q[i]) {
      if (w)
        add(y, w);
      else
        ans += (sum[x][y] == get(y));
    }
  }
  cout << n * m - ans << endl;
}

int main() {
  ios_fast;
  // freopen("test_output.txt","w",stdout);
  // freopen("test_input.txt","r",stdin);
  int TEST = 1;
  // cin >> TEST;
  while (TEST--) solve();
}

/*

*/

View Code

二 . POJ 2352 stars 【二维偏序模板】

三 . 其实树状数组求逆序对本质上也是一种二维偏序的问题哦，因为在一个二维的坐标平面上，逆序对的定义就是：\( i < j \) but \( a_{i} > a_{j} \)。

四 . 另一道练习题： Moving Points 【CF】这道题：要么一开始就是最短距离，要么以后会撞上，然后离散化一下，如果\( i < j \) but \( v_{i} > v_{j} \) 那么就说明会碰撞，其它情况下不会碰撞，最后总距离减去会碰撞的距离就是答案。

178： Discount【基环内向树】

（1）先要看出一共有n条边，这样就形成了一棵【基环内向树】tarjan取环，注意细节

（2）考虑DP，先进行外树的DP，定义:

\( f_{i,0} 为第 i 个物品打折购买/赠送而来的最小花费 \)

\( f_{i,1} 为第 i 个物品原价购买，不打折的最小花费 \) - - 这样就可以更加方便转移状态了

（3）树DP完了之后，就要进行环DP，我们考虑任取一个起点，然后终点如果和起点有联系，那么必然是购买终点赠送起点。这样就是① 以起点开始DP ② 强制购买终点再开始从起点DP【强制就是修改初始状态而已】

我们发现，强制购买终点如果会使得答案更优，可以看成是一次从终点作为开头的DP。那么做两次DP即可。

#include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define lowbit(x) (x & (-x))
#define ll long long
#define ull unsigned ll
#define mp make_pair
#define me(a, b) memset(a, b, sizeof(a))
#define emp push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define fi first
#define se second
#define ls (ro << 1)
#define rs (ls | 1)
#define mseg ((l + r) >> 1)

const int maxn = 2e5 + 11, inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, mod = 998244353;

ll n, p[maxn], d[maxn], f[maxn][2], g[maxn][2], vis[maxn], Timer;
int dfn[maxn], low[maxn], st[maxn], sz, tot, inc[maxn];
vector<vector<int>> e;
vector<int> loop;

inline void tarjan(int x) {
  vis[x] = Timer, st[++sz] = x;
  dfn[x] = low[x] = ++tot;
  for (int& v : e[x]) {
    if (!dfn[v] && !vis[v]) {
      tarjan(v);
      low[x] = min(low[x], low[v]);
    } else if (vis[v] == vis[x]) {
      low[x] = min(low[x], dfn[v]);
    }
  }
  if (dfn[x] == low[x]) {
    int tg = 0;
    while (st[sz] != x) tg = 1, inc[st[sz]] = 1, loop.push_back(st[sz--]);
    if (tg) loop.push_back(x), inc[x] = 1;
    sz--;
  }
}

inline void dfs(int x) {
  f[x][1] = p[x], f[x][0] = p[x] - d[x];
  for (int& v : e[x])
    if (!inc[v] && v != x) {
      dfs(v);
      f[x][0] += f[v][0], f[x][1] += f[v][0];
    }
  for (int& v : e[x])
    if (!inc[v]) f[x][0] = min(f[x][0], f[x][1] - p[x] + f[v][1] - f[v][0]);
}

inline ll DP(int L, int R) {
  g[L - 1][0] = f[loop[L - 1]][0], g[L - 1][1] = f[loop[L - 1]][1];
  for (int i = L, id; i < R; i++) {
    id = loop[i];
    g[i][0] = min(g[i - 1][0] + f[id][0], g[i - 1][1] + f[id][1] - p[id]);
    g[i][1] = g[i - 1][0] + f[id][1];
  }
  return g[R - 1][0];
}

inline void solve() {
  cin >> n, me(inc, 0);
  e.assign(n + 1, vector<int>());
  ll ans = 0;
  for (int i = 1; i <= n; i++) cin >> p[i];
  for (int i = 1; i <= n; i++) cin >> d[i];
  for (int x, i = 1; i <= n; i++) {
    cin >> x;
    if (x == i)
      loop.push_back(x);
    else
      e[x].push_back(i);
  }

  for (int& v : loop)
    if (!vis[v]) tarjan(v), dfs(v), ans += f[v][0];
  loop.clear();

  for (int i = 1; i <= n; i++) {
    if (vis[i]) continue;
    loop.clear(), tot = 0, Timer++, tarjan(i);
    if (loop.empty()) continue;
    for (int& v : loop) dfs(v);
    loop.push_back(loop.front());
    ans += min(DP(1, loop.size() - 1), DP(2, loop.size()));
  }
  cout << ans << endl;
}

int main() {
  ios_fast;
  // freopen("test_output.txt","w",stdout);
  // freopen("test_input.txt","r",stdin);
  int TEST = 1;
  // cin >> TEST;
  while (TEST--) solve();
}

/*

*/

View Code

179：Holes 【二分 + 贪心验证？】

感觉要真的去验证一个len是需要一定思维的。

参考了一个题解： link

考虑二分出mid，去验证mid的可行性【令 len = mid】

我们知道一个洞可以使得 \( 2 * len + 1 \) 个节点的距离都在 \( len \) 之内。【令 \( L = 2 * len + 1\)】

令 \( needlen \) 为贪心完之后，剩余的最长部分， \( maxlen \) 为贪心完之后，能够向外伸长多少。

① 对于链我们可以先贪心地减去 \( L \) 的节点，直到剩余长度 \( lef < L \)。

　　这个时候又有两种情况：

　　（1） \( lef <= len \) ：这种情况下，我们考虑在 root 上放一个洞，就能覆盖剩余部分，所以更新 \( needlen \) 即可

　　（2） \( lef > len && lef < L \) ：这时，我们必须再加一个树洞，因为这里是不会被其它地方覆盖的，同时更新 maxlen。

② 对于环，我们首先考虑贪心，如让剩余部分平均最短。

我们发现能减的长度永远都是 \( k * L \) 。所以平均最短的方式就是让两端剩下：\( ( circle_len % L ) / 2 \)

　　同样，分类讨论一下，更新maxlen和needlen。

int n, m, k, du[maxn], root, vis[maxn];
vector<vector<int>> e;
vector<int> li, ci;
 
inline int OK(int len) {
  int res = 0, maxlen = -1, needlen = 0, L = (2 * len + 1);
  for (int& v : li) {
    if (v <= len) {
      needlen = max(needlen, v);
    } else {
      res += v / L;
      if (v % L > len)
        maxlen = max(maxlen, L - (v % L) - 1), res++;
      else
        needlen = max(needlen, v % L);
    }
  }
  for (int& v : ci) {
    if (v <= len) {
      needlen = max(needlen, (v + 1) / 2);
    } else {
      res += v / L;
      if (((v % L) + 1) / 2 > len)
        maxlen = max(maxlen, L - 1 - ((v % L) + 1) / 2), res++;
      else
        needlen = max(needlen, ((v % L) + 1) / 2);
    }
  }
  if (needlen > maxlen) res++;
  return res <= k;
}
 
inline void work(int rt) {
  me(vis, 0);
  for (int& v : e[rt]) {
    if (vis[v]) continue;
    vis[v] = 1;
    int cur = v, cnt = 0, fa = rt, tg = 1;
    while (e[cur].size() && cur != rt && tg) {
      cnt++, tg = 0;
      for (int& nxt : e[cur])
        if (!vis[nxt] && nxt != fa) {
          if (nxt != rt) vis[nxt] = 1;
          fa = cur, cur = nxt, tg = 1;
          break;
        }
    }
    if (cur == rt)
      ci.push_back(cnt);
    else
      li.push_back(cnt);
  }
}
 
inline void solve() {
  cin >> n >> m >> k;
  e.assign(n + 1, vector<int>());
  for (int i = 1, x, y; i <= m; i++) {
    cin >> x >> y, du[x]++, du[y]++;
    e[x].push_back(y), e[y].push_back(x);
  }
  root = 1;  // 链与环
  for (int i = 1; i <= n; i++)
    if (du[i] > 2) root = i;
  work(root);
  int l = 0, r = n, mid;
  while (l < r) {
    mid = (l + r) >> 1;
    OK(mid) ? r = mid : l = mid + 1;
  }
  cout << r << endl;
}

View Code

180 ： transform 【二分 + 思维】

二分能拿多少点，然后计算最小花费，拿最小花费和T比较。

由于二分不能是整块，会剩下lef在 \( [L, R] \) 左或者右，但不会同时都有。【除非两边到中间的距离相等】

不知道是不是二分细节写错了还是怎么的，一直都是 83%。。。

181：message【维护凸包计算最大斜率 + 公式转换】

奥，最后一个交点是吧，列一下公式，然后发现就是求最大斜率（x 【说得简单，你tm会？】

① \( y = c_i * x + d_i = c_j * x + d_j => x = -1 * (d_i - d_j) / (c_i - c_j) \)

　　然后就是 \( i , j \) 两个点的斜率了。

　　维护一个向上的突起结构【其实是凸包，未封闭而已】，然后在这个凸包上三分。

② 三分的细节要写好

inline int Search(int a[], int l, int r) { 
  // 三分应该使用闭区间？【左闭右开的方法还没验证过 】
  int lm, rm;
  while (l <= r) {  // 闭区间使用=号即可
    lm = l + (r - l) / 3;  // (r-l)/3不是(r-l+1)/3，以后如果有冲突建议加深理解
    rm = r - (r - l) / 3;
    int lans = a[lm], rans = a[rm];
    if(lans <= rans) r = rm - 1; // 注意这个等号 = ！！！
    else l = lm + 1; 
  }
  return a[l]; // 为什么返回 l 而不是 r ？
}

说明：为什么等号 = 要放在\( r \)边界的更新处？为什么最后返回的是 L ？

　　考虑我们三分到最后，出现了 lm == rm 的情况，这个时候我们该怎么办？由于我们使用的是闭区间，那么必然让其中一个向内靠拢，要么 \(r = rm-1\) ,要么 \(l = lm+1\) ，考虑到最后返回的是 \( l \) ，我们这里让 r 产生变化，最后 l 才是正确的。

const int maxn = 2e5 + 11, inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, mod = 998244353;
const double eps = 1e-6;

double ans[maxn];
int n, m, top;

struct Point {
  double x, y;
  int id;
  Point operator-(const Point& b) { return {x - b.x, y - b.y, 0}; }
} p[maxn], s[maxn];

inline double cross(const Point& a, const Point& b) {
  return b.y * a.x - a.y * b.x;
}

inline bool cmp(const Point& a, const Point& b) {
  return (a.x == b.x && a.y < b.y) || (a.x < b.x);
}

inline double calc(const Point& a, const Point& b) {
  if (fabs(a.x - b.x) < eps) return -inf_ll;
  return -1 * (a.y - b.y) / (a.x - b.x);
}

inline void work() {
  top = 0;
  for (int i = 1; i <= n + m; i++) {
    if (p[i].id) {
      int l = 1, r = top + 1, lm, rm;
      while (l < r) {
        lm = l + (r - l) / 3;
        rm = r - (r - l) / 3;
        // cerr << l << " , " << r << endl;
        double la = calc(p[i], s[lm]), ra = calc(p[i], s[rm]);
        ans[p[i].id] = max({ans[p[i].id], la, ra});
        if (ra < la)
          r = rm - 1;
        else
          l = lm + 1;
      }
    } else {
      while (top > 1 && cross(s[top] - s[top - 1], p[i] - s[top - 1]) > 0)
        top--;
      s[++top] = p[i];
    }
  }
}

inline void solve() {
  cin >> n;
  for (int i = 1; i <= n; i++) {
    cin >> p[i].x >> p[i].y;
    p[i].id = 0;
  }
  cin >> m;
  for (int i = n + 1; i <= n + m; i++) {
    cin >> p[i].x >> p[i].y;
    p[i].id = i - n, ans[i - n] = -inf_ll;
  }

  sort(p + 1, p + 1 + n + m, cmp), work();
  for (int i = 1; i <= n + m; i++) p[i].x *= -1, p[i].y *= -1;
  sort(p + 1, p + 1 + n + m, cmp), work();

  for (int i = 1; i <= m; i++) {
    if (ans[i] <= 0)
      cout << "No cross" << endl;
    else
      cout << fixed << setprecision(10) << ans[i] << endl;
  }
}

View Code

182：D. Hemose in ICPC ?【利用欧拉序的连通性维护边的信息 + 二分】

① 跑一遍dfs获取欧拉序，这个欧拉序是遍历序，不是括号序。【然后你发现，欧拉序两两相邻的节点之间就是一条边！】

【然后1 - 2 - 1每条边都出现了两次，这也就是为什么欧拉序的长度是2*n-1，因为n-1条边出现了两次，2*n-2个空隙】

② 二分的细节：由于欧拉序相邻节点有一条边，所以我们二分出mid的时候，应该搜索的是\( [ l, mid ] 和 [mid, r] \) 而不是\( [mid+1, r] \)，因为mid和mid+1之际爱你还有一条边不能被忽视！

最后二分区间长度为2时，就可以得到答案了。

183：防线【树状数组维护前缀最小值 + 前后缀预处理 + 思维】

紫书上的题，使用树状数组维护【前缀最小值】常数小呀！内存少啊！

184：不无聊的序列【分治 + 思维 + 从两边往中间搜索】

考虑为什么复杂度是\( O(n * logn) \)的。

#include <bits/stdc++.h>
using namespace std;
#define ios_fast ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define lowbit(x) (x & (-x))
#define ll long long
#define ull unsigned ll
#define lld long double
#define mp make_pair
#define me(a, b) memset(a, b, sizeof(a))
#define emp push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define fi first
#define se second
// #define ls (ro << 1)
// #define rs (ls | 1)
#define mseg ((l + r) >> 1)

const int maxn = 2e5 + 11, inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, mod = 1e9 + 9;

map<ll, int> pos;
ll n, a[maxn], L[maxn], R[maxn];

inline int work(int l, int r) {
  if (l >= r) return true;
  int tmpl = l, tmpr = r, p = 0;
  while (tmpl <= tmpr && !p) {
    if (L[tmpl] < l && R[tmpl] > r)
      p = tmpl;
    else if (L[tmpr] < l && R[tmpr] > r)
      p = tmpr;
    tmpl++, tmpr--;
  }
  if (!p) return false;
  return work(l, p - 1) && work(p + 1, r);
}

inline void solve() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> a[i], R[i] = n + 1, L[i] = 0;
  pos.clear();
  for (int i = 1; i <= n; i++) L[i] = pos[a[i]], pos[a[i]] = i;
  pos.clear();
  for (int i = n; i > 0; i--)
    R[i] = pos.count(a[i]) ? pos[a[i]] : n + 1, pos[a[i]] = i;
  cout << (work(1, n) ? "non-boring" : "boring") << endl;
}

int main() {
  ios_fast;
  // freopen("test_output.txt", "w", stdout);
  // freopen("test_input.txt", "r", stdin);
  int TEST = 1;
  cin >> TEST;
  while (TEST--) solve();
}

/*
*/

View Code

185：K. Parabolic sorting【思维 + 树状数组维护交换过程】

不难吧这道题，首先求出一个数向左/向右交换次数是可以用树状数组求出来的，而且对答案的贡献也是独立的。

所以我们只需要考虑每个数向左还是向右即可，即\( ans += min(lef[i],rig[i]) \)

186：J. Something that resembles Waring's problem 【数学 + 思维 + 构造】

题目要求将一个正整数分解成为立方和：

\( N = a^3_1 + a^3_2 + a^3_3 + a^3_4 + a^3_5 \)

这种类型的题目之前已经做过了，2021ICPC网络赛的power sum就是类似的构造。

我们应该通过立方和之间的加减，消掉3次方项和2次方项，然后构造出1次方项。

然后通过神秘的力量才能够想出的：

\( (x - 1)^3 + (x + 1)^3 - x^3 - x^3 = 6 * x \)，这样我们通过四项就能够表示出6的所有倍数，我们可以让剩下的第五项表示那个余数。

然后对于输入的\( N \) ，我们有： \( N = 6 * x + t^3 \)。

所以应该构造一个，然后多出的或者少了的部分用x来消除掉或者补上： \( t^3 \% 6 == N \% 6 \)。

然后我们枚举1~10，发现1~5恰好就有 \( i^3 % 6 = i \)的神奇特性，这还怎么说，直接写代码去了。

呃，所以\( N = 6 * ( N//6 - (N\%6)^3 // 6 ) + (N\%6)^3 \) 其中\( // \) 指的是整除，减号是因为要抵消掉。

注意使用python写的代码，改写括号的地方还是要写的。

n = int(input())
x = (n//6) - (((n%6)**3)//6)
t = n%6
print("5\n{0} {1} {2} {3} {4}".format(x-1, x+1, -x, -x, t))

187-188：A word game 、Men's showdown【博弈论+SG函数裸题】

关于SG函数的讲解：LINK

好像是SG函数的转移可以通过mex来求值。

也就是当前状态为 \( u \) ，\( u \) 的下一个状态可能有： \( v_1 , v_2 , v_3 ...\) ，那么\( SG(u) = mex\{mex(v_1),mex(v_2),mex(v_3),......\} \) 。

也就是在后继状态的mex集合中求一个新的mex，这个值就是u的SG值。

例题一：很明显的nim博弈，但是只能拿1，2，all个石子。也就是说有三种状态，那么我们直接预处理出所有的SG函数即可。

例题二：也是一个明显的nim博弈，每次只能拿1，5，13个石子，那么直接预处理即可。

sg函数的预处理一定要记忆化呀！

sg = [-1 for _ in range(100)]


def get_sg(x):
    global sg
    if not x:
        sg[x] = 0
        return sg[x]
    if sg[x] != -1:
        return sg[x]
    st = set()
    st.add(0)
    if x >= 1:
        st.add(get_sg(x-1))
    if x >= 2:
        st.add(get_sg(x-2))
    for i in range(x + 1):
        if i not in st:
            sg[x] = i
            break
    return sg[x]


for i in range(41):
    get_sg(i)
s, a, flag = input(), [0 for _ in range(26)], 0
for ch in s:
    a[ord(ch) - ord('A')] += 1
for i in a:
    flag ^= sg[i]
print("Alice" if flag else "Bob")

例题一

sg = [-1 for _ in range(100001)]


def get_sg(x):
    global sg
    if not x:
        sg[x] = 0
        return sg[x]
    if sg[x] != -1:
        return sg[x]
    if x >= 5:
        sg[x] &= get_sg(x-5)
    if x >= 1:
        sg[x] &= get_sg(x-1)
    if x >= 13:
        sg[x] &= get_sg(x-13)
    sg[x] = not sg[x]
    return sg[x]

def get_sg2(x):
    global sg
    if sg[x] != -1:
        return sg[x]
    if not x:
        sg[x] = 0
        return sg[x]
    st = set()
    if x >= 1:
        st.add(get_sg2(x-1))
    if x >= 5:
        st.add(get_sg2(x-5))
    if x >= 13:
        st.add(get_sg2(x-13))
    for i in range(x):
        if i not in st:
            sg[x] = i
            break
    return sg[x]


print("2" if get_sg2(int(input())) else "1")

V例题二

189-191：奇怪的股市、Spying Game、Accounting Numeral System【数学归纳法证明 + 思维】

例题一：紫书上的题目。

例题二：题意：假设存在一个有向图一共有n个节点，起点为m（入度为0）。假设\( D_i \) 为\( m \) 到 \( i \) 的所有路径数量，请你构造一种方式，是的形成的图符合\( D \)数组的数量。【注意可能有多个节点的\(D\) 为0，可以视他为孤立点，不需要连边。】

例题三：训练题。

显然，一二题运用的都是同一个结论，如果已经知道 \( a_1 + .. + a_n \) 能组成 \( X \) ，那么贪心地选就能构造出一个解。

但是例题三好像有点难证。

192：Ideal Farm【构造 + 数学 + 贪心】

题目大意：有\( s \) 个动物，\( n \) 个猪圈（假设猪圈从1~n连成一个序列），如果对于任意一种分法，都能满足①每个猪圈都有动物②存在一个区间[l,r]，区间的猪圈动物之和为k，就输出Yes，反之输出No。

1）把问题转化：有一个长度为\( n \) 的数组 \( a \) ，给出 \( \sum a_i = S \) ，现在问你这个数组是否一定存在一个子区间和为 \( k\)。

直接想很难做，所以考虑转化。转化成为前缀和k的同余系，我们发现，如果我们从1~S之间，选了n个数【默认\(sum_0 = 0\) 】，这n个数作为前缀和两两只差都不等于k，那么说明我们成功构造出一组反例说明这个数组可以不存在子区间和为k。所以输出No即可。

我们发现，我们只需要尽最大的努力去构造这样的反例，就能直接输出No，（由于我们的构造方法是足够有效的，甚至可以当作等价命题）对于无法构造的，我们只能输出Yes了。

2）考虑如何构造，也就是让尽可能多的数出现，而且两两之差不为k：

看一个例子：其中S = 13，k = 3 【使用竖线分组，0是本来存在的，不属于任何一组】

0 | 1 2 3 4 5 6 | 7 8 9 10 11 12 | 13 【有一个0是因为\( sum_0 = 0 \) 】

尽可能地选，让\( for \space every \space i,j \space sum_i - sum_j != k \) 。【注意，6 7 8 虽然是连续k个数，但是8-6不等于k】

可以看出，就是把 S 先分成 \( S//(2*k) \) [// 指整除] 份，完整的分组有\(S//(2*k)*k\)个，然后剩下的余数部分，只能选前 k - 1个。

然后就愉快通过此题了。【重在构造反例，其实构造反例也可以充当一个充要条件】

upd: 这道题甚至跟贪心有点关系？

翻了一下cf题解和其它题解，总的思路就是贪心地选数，使得前缀和两两之间的差值不等于k，然后就是从小到大选嘛，所以直接贪心地选就是了。

【还有就是，为什么CF题解里是2*n+1个数，然后值域为[1,s+k]，其实这和2*n+2个数，值域和[0,s+k]一样的吖，我是sb纠结半天。】

然后最近又翻到离散数学课本上的一道相似的例题：【显然例题更简单】

在30天的一个月里，某球队一天至少打一场比赛，30天下来至多打45场。证明一定有连续若干天内，这个队打了14场比赛。

证明：套路取前缀和数组，\( s_0 = 0, s_1,s_2 ... s_{30}, s_0 + 14,s_1 + 14,s_2+14 .... s_{30}+14\) 。

这里有62个数嘛，然后每个数的取值范围是[0, 45 + 14] -> [0, 59]。

62个数放在60个数的桶里面一定会有重叠的吧。

// AC code
  cin >> s >> n >> k;
  if (s == k) {
    cout << "YES" << endl;
  } else if (k > s) {
    cout << "NO" << endl;
  } else {
    ll num = (s / (2 * k)) * k + min(k - 1, s % (2 * k));
    if (num < n) {
      cout << "YES" << endl;
    } else {
      cout << "NO" << endl;
    }
  }

View Code

193：专题 . 鸽巢原理/抽屉定理【思维 + 构造】

例题一：Find a Multiple【POJ】

考察的是前缀和抽屉原理，由于0~n的前缀和共有n+1个，在模除n的情况下，只会出现n个数，n+1个前缀和放在n个同余系里，那必然会出现重复的情况，所以我们使用一个pos标记一下上一个出现的位置即可。

例题二：F. Double Knapsack【CF 构造 + 思维 + 抽屉原理】

好难啊！！！【此题来源于一个古老的俄罗斯数学：LINK】

1）我们首先不考虑一个问题：为什么集合能变成序列【这个问题不需要考虑，是因为我们的构造算法可以通过序列解决此问题】

2）如果只是考虑两个数组，a，b中分别找一段连续序列之和相等，那么就有等式：

\( sumA_i - sumA_j = sumB_u - sumB_v \)

\( => \space sumA_i - sumB_u = sumA_j - sumB_v \)

我们发现：i，j，u，v分别是4个变量，我们应该怎么选他们呢？

答案就是：对于i我们选一个最大的u，使得\( sumA_i >= sumB_u \) ，别忘了等号。对于j同理。

由于题目规定：\( a_i <= n , b_j <= n \) 所以，我们这样构造，得出有 \( 0 ≤ sumA_i - sumB_u < n \)。

既然值域是0~n-1的，又有n+1个前缀和，那至少有两个重合，所以必定有答案。

3）注意一下代码的结构，我们应该怎么输出呢？

由于我们已经说过是连续序列了，所以直接从 \( j -> i , v -> u \) 输出即可。

const int maxn = 1e6 + 11, inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, mod = 1e9 + 7;

ll n, a[maxn], b[maxn], sa[maxn], sb[maxn];
using PLLL = tuple<ll, ll, ll>;
PLLL p[maxn];

inline int work(ll sa[], ll sb[], int tg) {
  int ptr = 0;
  for (int i = 0; i <= n; i++) {
    while (ptr < n && sb[ptr + 1] <= sa[i]) ptr++;
    p[i] = make_tuple(sa[i] - sb[ptr], i, ptr);
  }
  
  sort(p, p + 1 + n);

  for (int i = 0; i < n; i++) {
    if (get<0>(p[i]) == get<0>(p[i + 1])) {
      PII L = mp(get<1>(p[i]), get<2>(p[i]));
      PII R = mp(get<1>(p[i + 1]), get<2>(p[i + 1]));
      if (tg) swap(L.fi, L.se), swap(R.fi, R.se);
      cout << R.fi - L.fi << endl;
      for (int t = L.fi + 1; t <= R.fi; t++) cout << t << " ";
      cout << endl << R.se - L.se << endl;
      for (int t = L.se + 1; t <= R.se; t++) cout << t << " ";
      cout << endl;
      return true;
    }
  }
  return false;
}

inline void solve() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> a[i];
  for (int i = 1; i <= n; i++) cin >> b[i];

  for (int i = 1; i <= n; i++)
    sa[i] = sa[i - 1] + a[i], sb[i] = sb[i - 1] + b[i];

  if (sa[n] >= sb[n]) {
    if (!work(sa, sb, 0)) cout << -1 << endl;
  } else {
    if (!work(sb, sa, 1)) cout << -1 << endl;
  }
}

View Code

194：Bring Your Own Bombs 【思维 + 离散化 + 简单概率论】

如果可能的话，当然是沿着炸弹横向遍历一遍，纵向遍历一遍，更新经过格子的爆炸概率，最后把所有格子爆炸的概率相加就是结果。

但是本题数据很大，不允许这样做。于是我们可以离散化。再对于每一个区域，找到横向（纵向）区域内的爆炸概率和。【这一部分可以使用线段树维护】

比如找到横向的爆炸概率和为p1,纵向为p2。那么这个区域内爆炸的期望数为：p1*(ry[i]-ly[i]+1) + p2*(rx[i]-lx[i]+1) - p1*p2

细节：

（1）使用vector 和 lower_bound，返回的index应该+1

（2）注意区分x和y，横向爆炸和纵向爆炸

const int maxn = 5e5 + 11, inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f3f, mod = 1e9 + 7;

ll n, m, lx[maxn], rx[maxn], ly[maxn], ry[maxn];
ll dx[maxn], dy[maxn];
double px[maxn], py[maxn], tr[2][maxn << 2];
vector<ll> hx, hy;

inline int IDx(ll x) { return lower_bound(all(hx), x) - hx.begin() + 1; }

inline int IDy(ll y) { return lower_bound(all(hy), y) - hy.begin() + 1; }

inline void update(int ro, int l, int r, int x, double v, int tp) {
  if (l == r) {
    tr[tp][ro] = tr[tp][ro] + v - tr[tp][ro] * v;
    return;
  }
  x <= mseg ? update(ls, l, mseg, x, v, tp) : update(rs, mseg + 1, r, x, v, tp);
  tr[tp][ro] = tr[tp][ls] + tr[tp][rs];
}

inline double query(int ro, int l, int r, int s, int e, int tp) {
  if (s <= l && r <= e) return tr[tp][ro];
  double ans = 0;
  if (s <= mseg) ans += query(ls, l, mseg, s, e, tp);
  if (mseg < e) ans += query(rs, mseg + 1, r, s, e, tp);
  return ans;
}

inline void solve() {
  cin >> n >> m;
  for (int i = 1; i <= n; i++) cin >> lx[i] >> ly[i] >> rx[i] >> ry[i];
  for (int i = 1; i <= m; i++) cin >> dx[i] >> dy[i] >> px[i] >> py[i];
  for (int i = 1; i <= n; i++) {
    hx.push_back(lx[i]), hx.push_back(rx[i]);
    hy.push_back(ly[i]), hy.push_back(ry[i]);
  }
  for (int i = 1; i <= m; i++) {
    hx.push_back(dx[i]), hy.push_back(dy[i]);
  }

  sort(all(hx)), hx.erase(unique(all(hx)), hx.end());
  sort(all(hy)), hy.erase(unique(all(hy)), hy.end());

  for (int i = 1; i <= m; i++) {
    px[i] /= 100.0, py[i] /= 100.0;
    update(1, 1, hx.size(), IDx(dx[i]), py[i], 0);
    update(1, 1, hy.size(), IDy(dy[i]), px[i], 1);
  }

  double ans = 0;
  for (int i = 1; i <= n; i++) {
    double t1 = query(1, 1, hx.size(), IDx(lx[i]), IDx(rx[i]), 0);
    double t2 = query(1, 1, hy.size(), IDy(ly[i]), IDy(ry[i]), 1);
    ans += (t1 * (ry[i] - ly[i] + 1) + t2 * (rx[i] - lx[i] + 1) - t1 * t2);
  }
  cout << fixed << setprecision(10) << ans << endl;
}

View Code

195-198：简单题提高信心吧

195：P7223 [RC-04] 01 背包【数学】

考虑每个数对答案的贡献，可以分为选和不选，那么对答案的贡献分别为：\( p^{a_i} 、1 \)

所以ans = \( \prod (qpow(p,a_i) + 1) \)

196：最大约数和【暴力求约数和 + 01背包】

此题数据范围太小啦！所以直接求出权值与体积，然后01背包即可。

197：荷马史诗【k进制下的huffman编码】

类似于：合并果子

此题应该是k叉huffman树的模板。

要注意的点就是：如果n不满足(n-1)%(k-1)，那么应该继续添加次数为0的节点，用来充填这棵树，把其他节点挤到更高的地方。

　　因为每次都是将k个节点合并为1个（减少k-1个），一共要将n个节点合并为1个，如果（n-1）%（k-1）！=0 则最后一次合并时不足k个。也就表明了最靠近根节点的位置反而没有被排满，因此我们需要加入k-1-（n-1）%（k-1）个空节点使每次合并都够k个节点（也就是利用空节点将其余的节点挤到更优的位置上）。

【你会发现，huffman树在一次操作之后仍然满足这个条件：（n-1）%（k-1） == 0，所以只需要一开始满足即可】

198：花匠【DP 、贪心】

定义：

f[i][0] 第i个节点为低谷的最长序列

f[i][1] 第i个点为高峰的最长序列

（1）如果 a[i] > a[i-1] 那么 a[i] 作为高峰就可以多加一个数

　　如果强行让 a[i] 作为低谷，这种状态并不合法，所以应该删掉 a[i] ，直接从 a[i-1] 继承

　　即 f[i][0] = f[i-1][0]，这样后续 a[i+1] > a[i] 时也可以继承到 a[i-1] 的状态

（2）如果 a[i] < a[i-1] 那么 a[i] 应该作为低谷。

　　反之也不合法，直接继承 i - 1 的状态。

贪心的话，好像直接模拟走高峰和低谷，在折点ans++就可以了

最后再开一个知识点的坑：差分约束系统习题

199：糖果【建图 + 拓扑排序 DP 求最长路差分约束系统】

根据≥、＞建图，或者根据≤，＜建图，反正就是求相对最大值，最后把等边拿出来特判一下就好了。

200：黑暗爆炸排队布局

熟悉的 Farmer John ，熟悉的奶牛，熟悉的味道

posted @ 2021-09-17 17:25 PigeonG 阅读(448) 评论(0) 收藏举报

刷新页面返回顶部

PigeonG

keep fighting!

ACM散题习题库 2【持续更新】

习题101~200：