吴恩达机器学习（1）单变量线性回归

• 模型

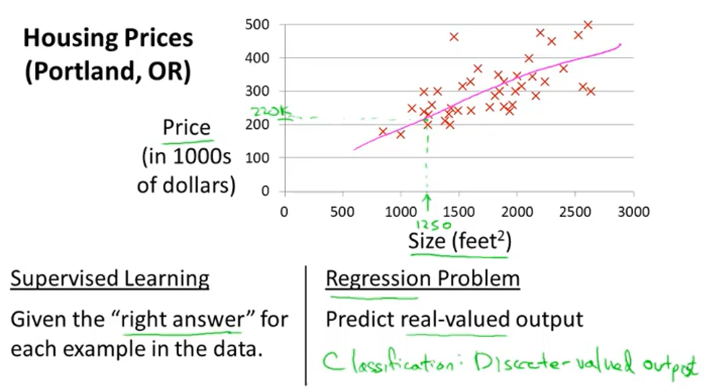
      以波特兰市住房价格为例子来引出一个单变量的线性回归问题。给出在不同面积下的住房价格数据集，通过找出其中的相近函数来预测不同面积下的住房价格。如下图所示：

      这个是一个监督学习问题，因为我们知晓了房子的面积以及相应面积下的住房价格；这也是一个回归的问题，我们需要预测一个实际的输出——房子的价格。另一个监督学习问题叫做分类问题，一般用来预测离散值输出。

      

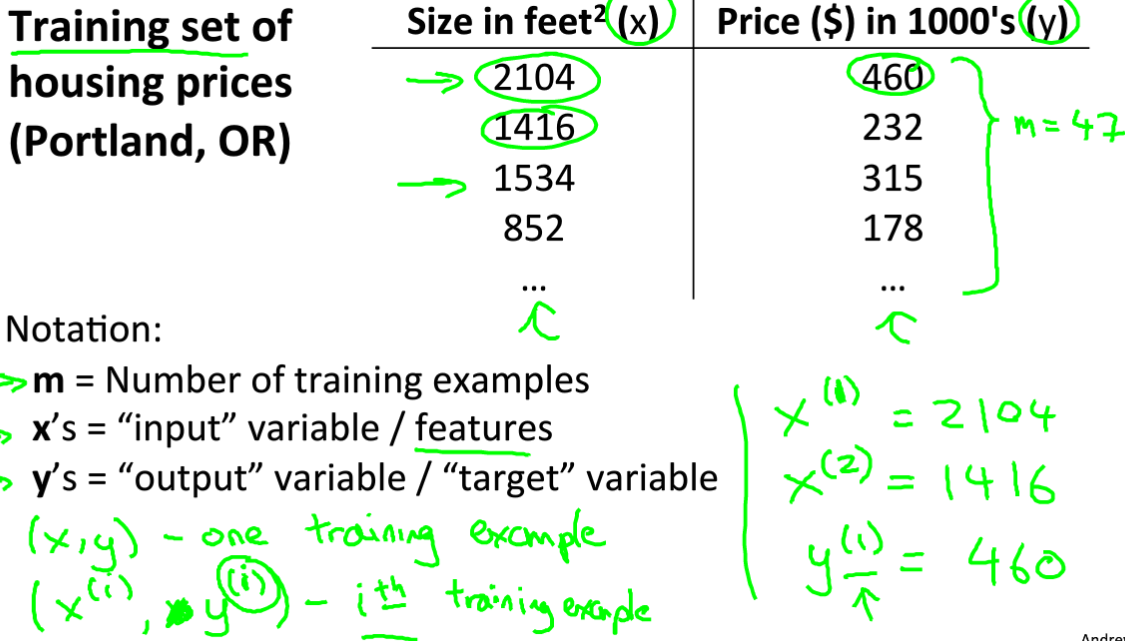
这是不同面积下房价数据集，在下面的模型中，m是训练数据集的容量，x表示输入，y表示输出，i表示第几个数据。

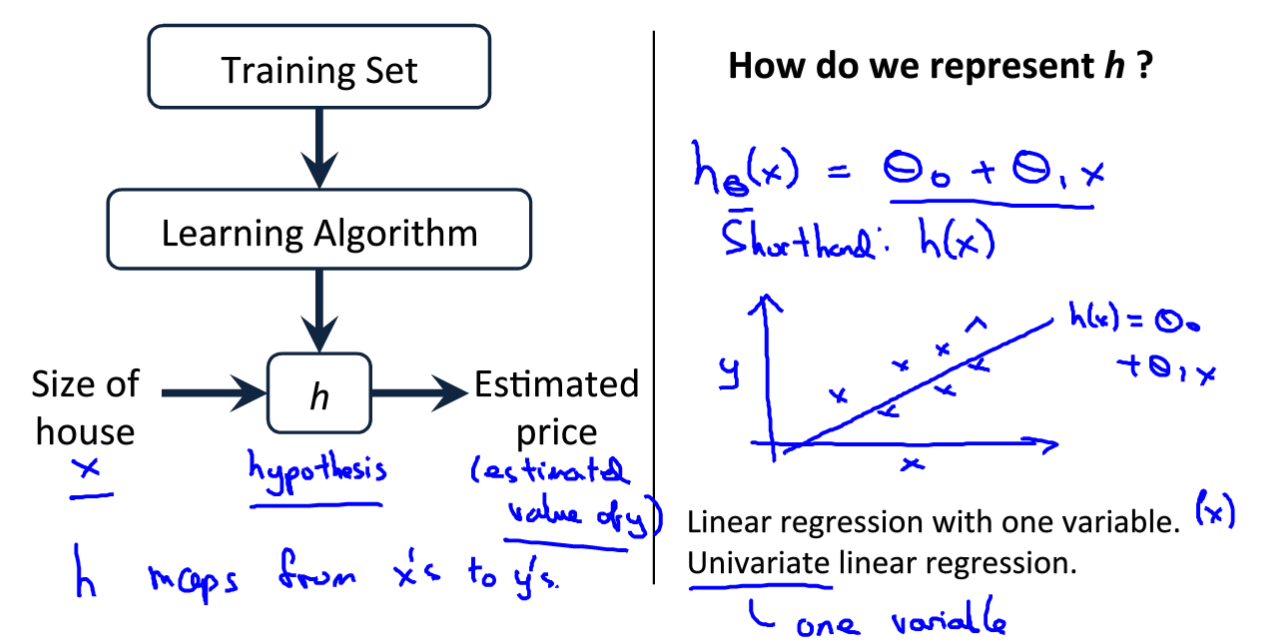
我们要完成的就是通过假设一个面积与房价的线性函数，通过上面的数据集进行拟合，最终达到输入一个任意大小的面积就能预测房价的目的。大致的框架如下如所示：

在下图中，h就是我们需要假设的线性函数，右图中的θ0，θ1是待定数值，需要通过数据集训练得到。

 

• 代价函数

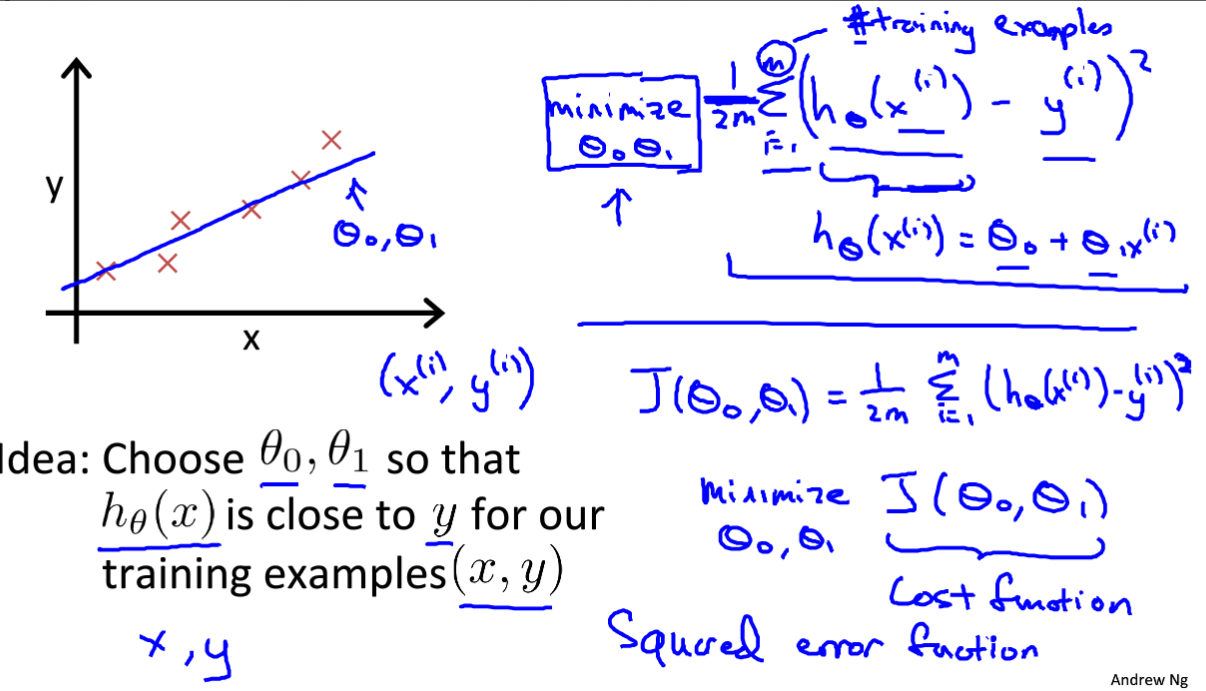
    在前到讲到了，我们假设函数h（x）= θ0 + θ1x，其中θ0，θ1是这个模型需要变化的参数，同使用m个数据集进行训练，找到模型参数，使拟合的函数能满足房价回归的结果。

那么怎样才怎判断这个拟合函数的正确度呢？这里引入代价函数，这个代价函数的意思是通过我们假设h（x）求解的房价与原本的房价的方差的1/2m，我们的目的就是找到θ0，θ1的值使整个代价函数最小。

这个代价函数也叫平方误差函数。

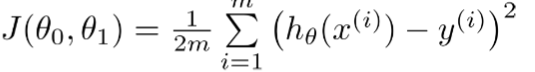
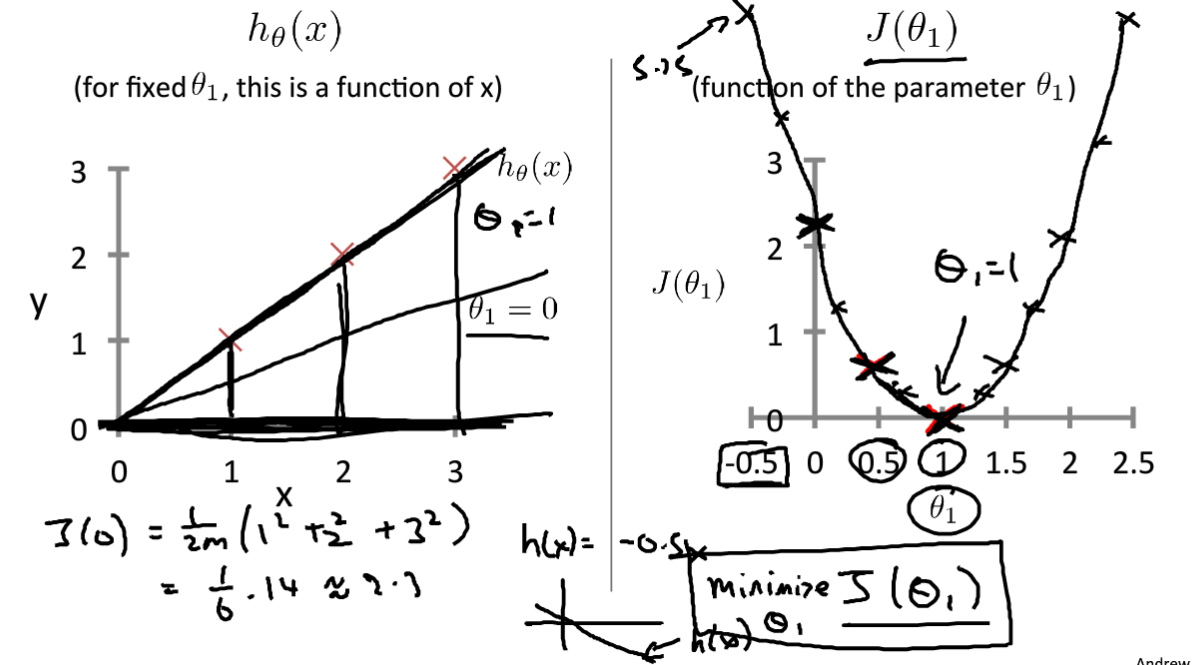
为了更好的理解这个过程，我们设定θ0 = 0，所以h(x) = θ1x。我们可以根据不同的θ1，来计算代价函数的值，如下图所示：

左图是根据不同的θ1确定的拟合函数计算输出值，右图是不同θ1下的代价函数计算值，最后可以得到大致的代价函数解析图，可以看到在θ1=1时候整个代价函数取值最小，这也是最后的解。

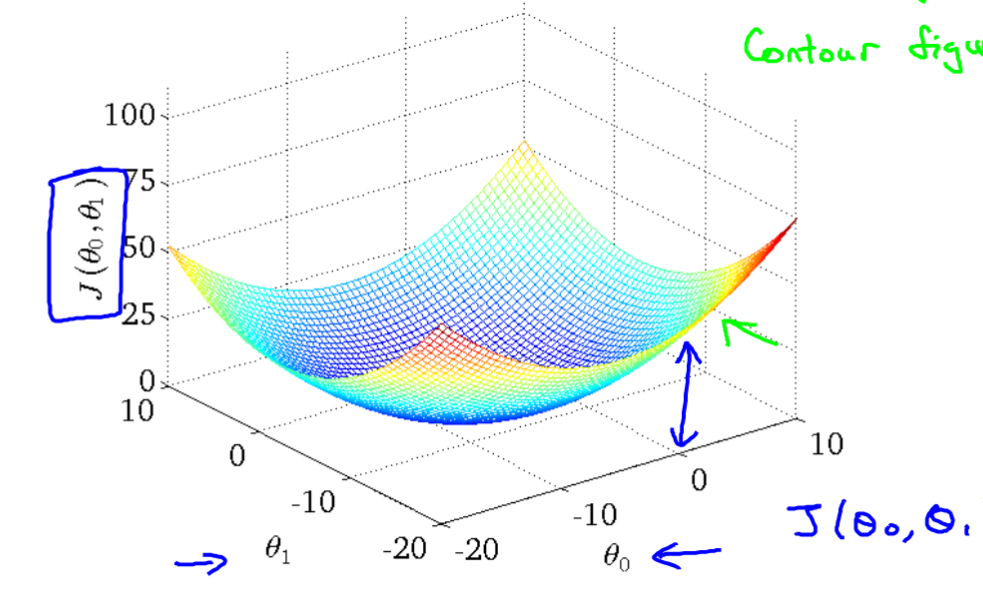
那么我们假设θ0不等于0，假设函数还是h（x）= θ0 + θ1x，根据理论，可以得到此时的代价函数的分布图：可以发现是一个三维的图。

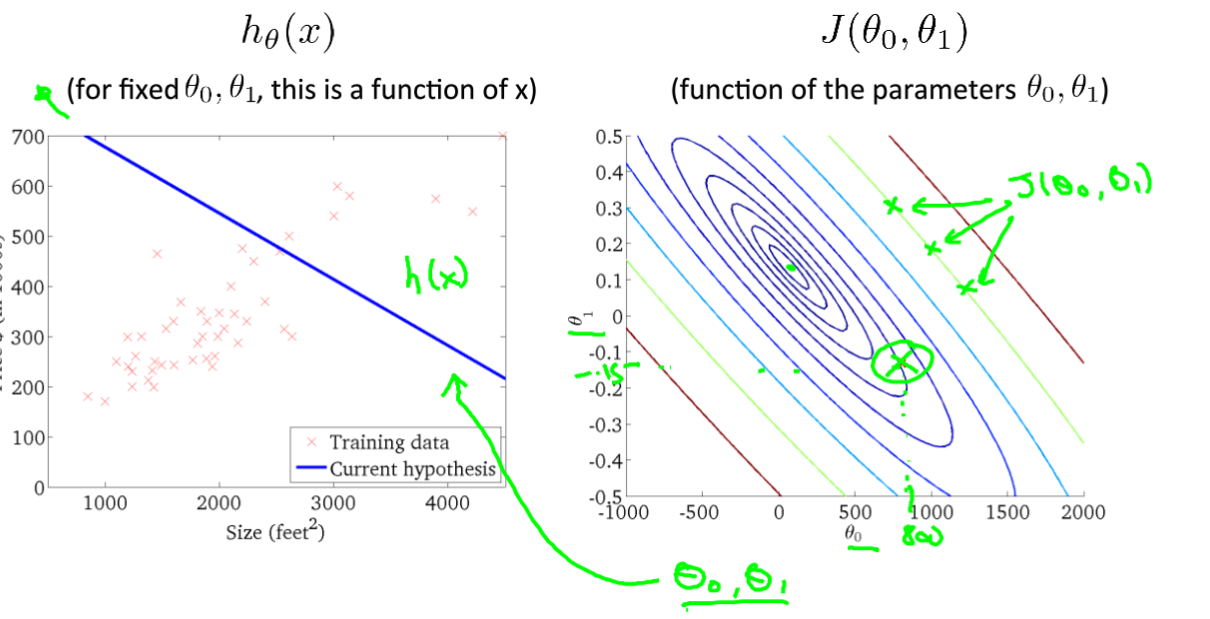
我们可以采用等高线的形式来观察，同一个椭圆的代价函数值是相同的；我们可以看到同心椭圆的中心就是代价函数的最优点，左侧是拟合的一个函数，右侧是相应的代价函数输出点位置。左侧的预测函数并没有很好的拟合数据集，所以右侧相应的

代价函数值就离最优点较远。

• 梯度下降法

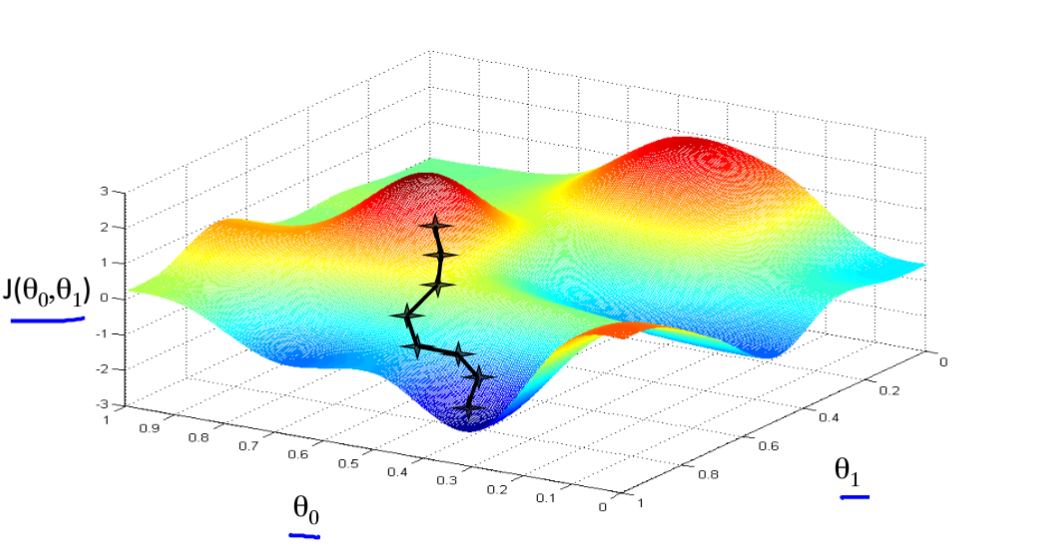
前面已经建立的拟合函数和代价函数，我们的目的就是找到使代价函数最小或者局部最小的θ0，θ1值。我们怎么才能达到这个目的呢， 我们这里使用梯度下降的方法来达到这个目的，这个方法被广泛应用到机器学习领域之中。梯度下降原理很简单，就是不停的改变θ0，θ1的值，让代价函数得到最小值或者局部最小值。首先我们来看看梯度下降是如何工作的：先初步定义θ0，θ1的值，如下图所示的最上面的点，从该点出发，找下降的方向一步一步下降，知道无法下降为止，此时的θ0，θ1值就是代价函数的最小值或者是局部最小值。

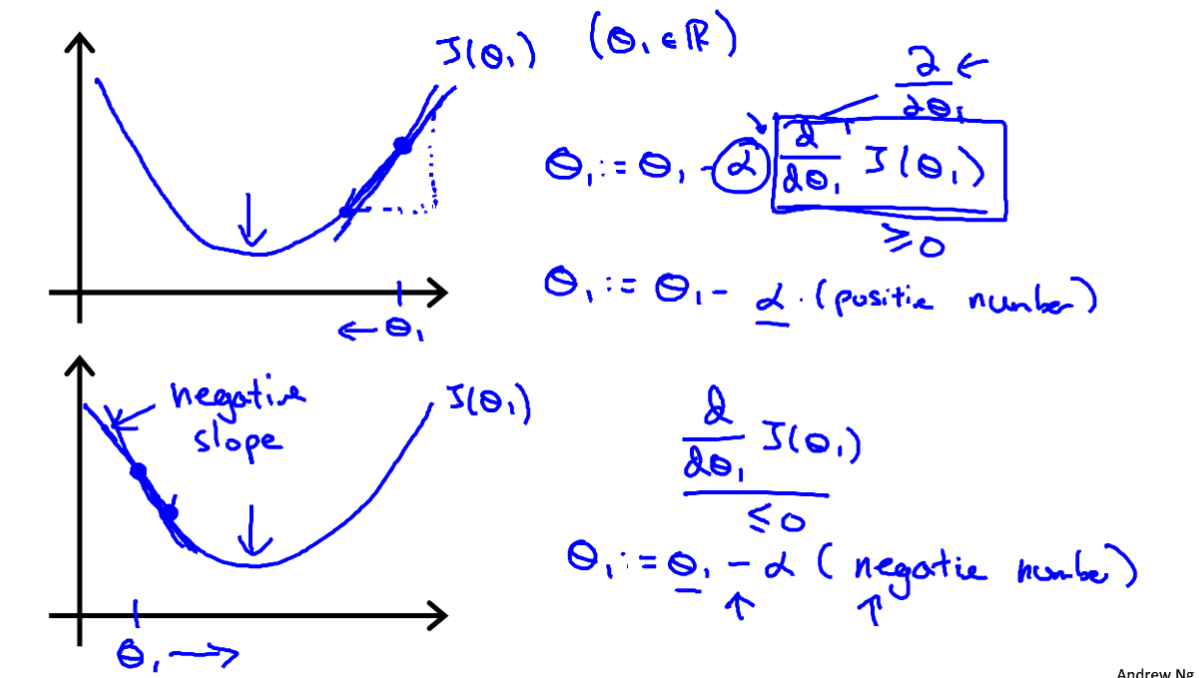
数学表达式：

梯度下降法就是把参数减去学习率与该参数的偏导数乘积，注意的是所有参数需要同时改变上图所示的右下图就是错误的例子。为了更好的理解可以选择只留下一个参数进行梯度下降展示：

 

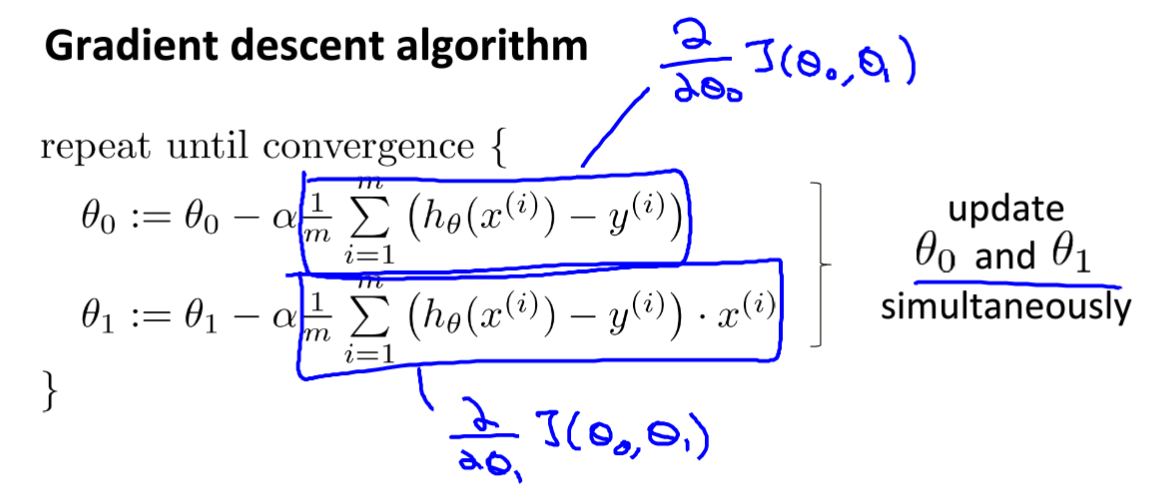
• 学习率

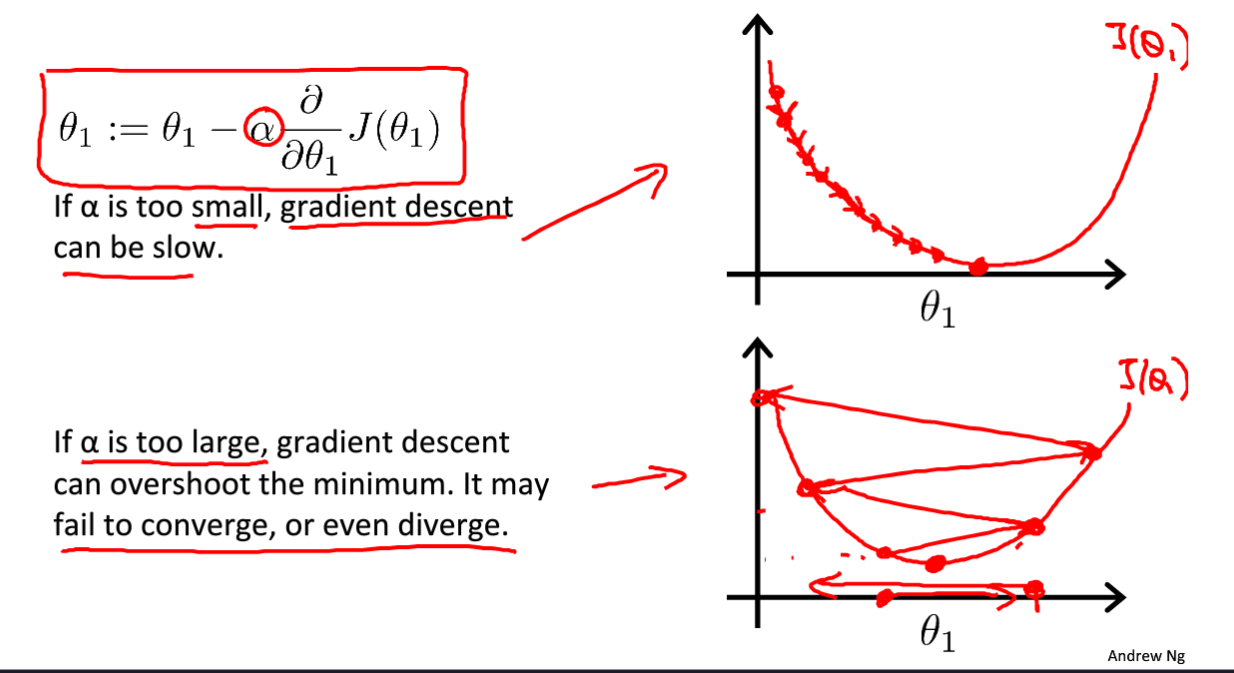
观察上面的公式我们可以发现，整个梯度下降过程的快慢实际上取决于学习率的大小，学习率大，梯度下降的快，但可能会错过最优的结果；学习率小，梯度下降慢，但精确。

所以需要根据实际的情况选择合适的学习率。