【笔记】函数和方程(2)

二分法求根

例1 编写二分法求根程序，求方程x^3+1.1x^2+0.9x-1.4=0实根的近似值，使误差不超过10^(-3)。

解：（1）求根的初始隔离区间。

在MATLAB工作区输入：

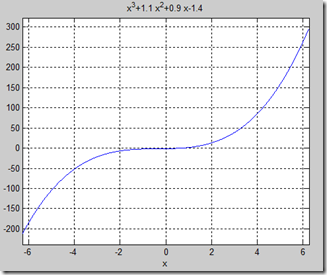
>> ezplot('x^3+1.1*x^2+0.9*x-1.4')
>> grid on

可以看出，根在区间(-2,2)中，进一步画出该部分图形：

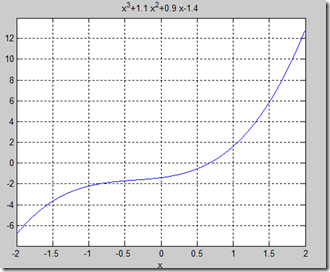
>> ezplot('x^3+1.1*x^2+0.9*x-1.4',[-2,2]),grid on

可以看出根在0,1之间。

（2）编写M文件：

% erfenfa.m
f=input('函数f(x)=');
qujian=input('区间=');
err=input('误差=');
a=qujian(1);
b=qujian(2);
yc=1;
while ((b-a)>err)&(yc~=0);
    c=(a+b)/2;
    x=a;
    ya=eval(f);
    x=b;
    yb=eval(f);
    x=c;
    yc=eval(f);
    if ya*yc<0
        b=c;
    else
        a=x;
    end
    x0=c
end

调用结果

>> erfenfa.m
函数f(x)='x^3+1.1*x^2+0.9*x-1.4'
区间=[0,1]
误差=0.001
x0 =
    0.5000

x0 =
    0.7500

x0 =
    0.6250

x0 =
    0.6875

x0 =
    0.6563

x0 =
    0.6719

x0 =
    0.6641

x0 =
    0.6680

x0 =
    0.6699

x0 =
    0.6709

由此得到方程的近似根为0.6709

牛顿迭代法求根

例2 编写牛顿迭代法求根程序，求方程x^3+1.1x^2+0.9x-1.4=0的实根的近似值，并计算迭代次数为6的近似根。

解：由例1知[0,1]是根的一个隔离区间，在[0,1]上

                          f(x)=x^3+1.1x^2+0.9x-1.4

                          f’(x)=3x^2+2.2x+0.9,   f’’(x)=6x+2.2

f’(x)及f’’(x)在[0,1]上保持同号，f(1)<0与f’’(1)同号，所以取x0=1为迭代初始值。

编写M文件如下：

f=input('函数:f(x)=');
n=input('请输入迭代次数:n=');
x0=input('请输入迭代初始值：x0=');
f1=diff(f);
format long
for i=1:n
    x=x0;
    fx0=eval(f);
    f1x0=eval(f1);
    x0=x0-fx0/f1x0
end

运行结果如下：

函数:f(x)='x^3+1.1*x^2+0.9*x-1.4'
请输入迭代次数:n=6
请输入迭代初始值：x0=1
x0 =
   0.737704918032787

x0 =
   0.674168811673928

x0 =
   0.670667575594511

x0 =
   0.670657310813841

x0 =
   0.670657310725810

x0 =
   0.670657310725810

由此得到，方程的根的近似值为  0.670657310725810。

例3 用牛顿法求下列方程的正根，要求精度e=10^-6。

x^2-3x+exp(x)=2

解：令f(x)=x^2-3x+exp(x)-2，当x>2,f(x)>0,f’(x)>0及f(x)恒正，所以根在[0,2]。先用图解法找初值，再用牛顿法程序newton.m求解。

>> fun=inline('x^2-3*x+exp(x)-2');
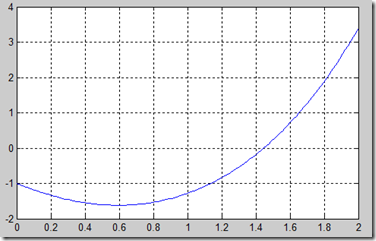
>> fplot(fun,[0,2]);grid on;

可见上述方程有唯一正根在1.5附近，取x0=1.5。

% M函数newton.m
function x=newton(fname,dfname,x0,e)
% 用途：用牛顿迭代法解非线性方程f(0)=0
% 格式：用x=newton(fname,dfname,x0,e)x返回数值解，fname,dfname分别表示
% f(x)及其导函数f'(x)，x0为迭代初值，e为精度要求（默认为1e-4）
if nargin<4,e=1e-4;end %默认精度为1e-4
x=x0;
x0=x+2*e;
% 这样做可以使while成立，且进入while后x0得到赋值
while abs(x0-x)>e
    x0=x;
    x=x0-feval(fname,x0)/feval(dfname,x0);
end

调用方法：

>> fun=inline('x^2-3*x+exp(x)-2')；
>> dfun=inline('2*x-3+exp(x)')；
>> newton(dun,dfun,1.5,1e-6)
>> newton(fun,dfun,1.5,1e-6)
ans =
   1.446238685966427

用MATLAB中的内部函数求根

例4
（1）用roots求方程x^9+x^8+1=0的根；
（2）用solve求上述方程的根；
（3）用fzero求方程x^2+4sinx=25的根；
（4）用fsolve求方程x=exp(-x)在0附近的根。

解：

（1）在MATLAB命令窗口中输入：

>> p=[1 1 0 0 0 0 0 0 0 1];
>> roots(p)

输出：

ans =
  -1.2131         
  -0.9017 + 0.5753i
  -0.9017 - 0.5753i
  -0.2694 + 0.9406i
  -0.2694 - 0.9406i
   0.4168 + 0.8419i
   0.4168 - 0.8419i
   0.8608 + 0.3344i
   0.8608 - 0.3344i

（2）在MATLAB窗口中输入：

>> solve('x^9+x^8+1')
输出：
ans =
 
                                          -1.2131497230596399145540815088108
    0.9405784010231450703309884633898*i - 0.26935193759657466239499735181026
- 0.57531209407289260277720483797049*i - 0.90172773557825296622423876941201
   0.57531209407289260277720483797049*i - 0.90172773557825296622423876941201
   0.84191977308465856032531749536099*i + 0.41683400653657232118306037529804
  - 0.9405784010231450703309884633898*i - 0.26935193759657466239499735181026
   0.33435225889790612035535442609416*i + 0.86082052816807526471321650032963
   0.41683400653657232118306037529804 - 0.84191977308465856032531749536099*i
   0.86082052816807526471321650032963 - 0.33435225889790612035535442609416*i

（3）首先作图，确定根的大致范围：

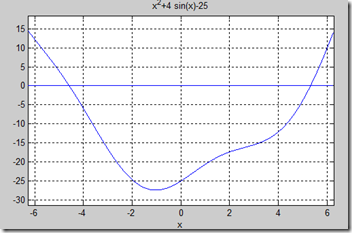
>> clf,ezplot x-x,grid on,hold,ezplot('x^2+4*sin(x)-25')

从图可以看出，两根在-4,5附近，再具体求根。

>> x1=fzero('x^2+4*sin(x)-25',-4)
x1 =
   -4.5861
>> x1=fzero('x^2+4*sin(x)-25',5)
x1 =
    5.3186

（4）在MATLAB命令窗口中输入：

>> fun=inline('x-exp(-x)');
>> x=fsolve(fun,0)
x =
    0.5671