网络流【网络最大流 + 最小网络最大流】
一、网络最大流
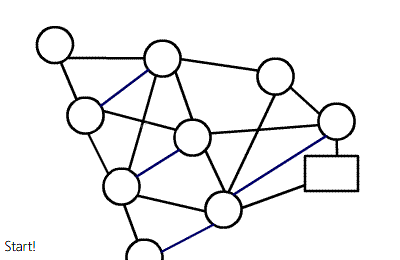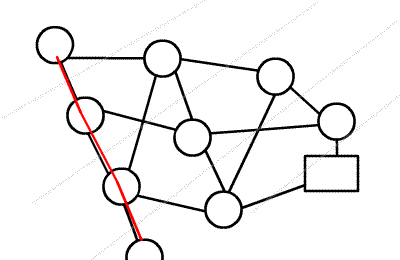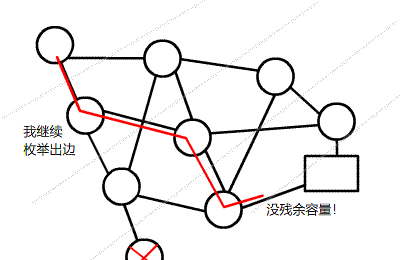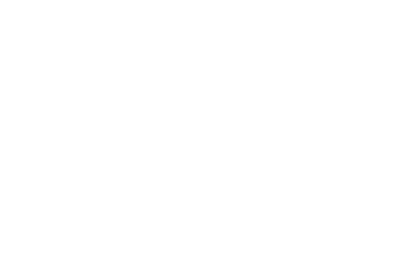
(从学委那里拿的动图。)
Dinic \text{Dinic} Dinic
/*
Dinic
在残留网络和 EK 的基础上,按照源点到该点的距离进行分层,每次寻找增广路径时,
保证每次都是从一层走到下一层。每次可寻找到多条增广路径
*/
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 205
#define maxm 10005
#define rep(i, a, b) for(int i = a; i <= b; ++i)
int n, m, s, t;
int cnt = 1, hd[maxn];
struct node{
int to, nxt, val;
}e[maxm];
int dep[maxn], ans;
int u, v, w;
inline void add(int u, int v, int w)
{
e[++cnt].to = v;
e[cnt].nxt = hd[u], e[cnt].val = w;
hd[u] = cnt;
}
inline bool bfs()
{
queue <int> q;
memset(dep, 0, sizeof dep);
dep[s] = 1, q.push(s);//注意初始源点为第一层
while(!q.empty())
{
int u = q.front();
q.pop();
for(int v, i = hd[u]; i; i = e[i].nxt)
{
if(e[i].val/*该边能走*/ and !dep[v = e[i].to]/*没有访问过*/)
{
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
if(dep[t]/*汇点可以到达,说明此时网络中有增广路径*/) return 1;
return 0;
}
inline int dinic(int u, int in/*从源点到达 u 点的流量*/)
{
if(u == t/*到达汇点*/) return in;
int out = 0;//记录能从 u 点流出的流量
for(int i = hd[u]; i and in/*当前还有流量可以流走*/; i = e[i].nxt)
{
int v = e[i].to;
if(dep[v] == dep[u] + 1/*只能往下一层走*/ and e[i].val/*当前边可以走*/)
{
int res = dinic(v, min(e[i].val, in)/*更新流入量*/);
e[i].val -= res, e[i ^ 1].val += res/*更新当前边流量*/;
in -= res, out += res;
}
}
if(!out/*没有流可以从 u 点流出去*/) dep[u] = 0/*优化,下一次不会再经过此点*/;
return out;
}
signed main()
{
scanf("%lld %lld %lld %lld", &n, &m, &s, &t);
rep(i, 1, m)
{
scanf("%lld %lld %lld", &u, &v, &w);
add(u, v, w), add(v, u, 0);
//残留网络,同时建反边,边权为 0,并以此判断该边能否通过
}
while(bfs()) ans += dinic(s, 1e16);//每次找完当前情况下的增广路径之后,重新分层
printf("%lld\n", ans);
return 0;
}
1、当前弧优化
“
注意在 DFS 中用 c u r [ x ] cur[x] cur[x] 表示当前应该从 x x x 的编号为 c u r [ x ] cur[x] cur[x] 的边开始访问,也就是说从 0 到 c u r [ x ] − 1 cur[x]-1 cur[x]−1 的这些边都不用再访问了,相当于删掉了,达到了满流。
D
F
S
(
x
,
a
)
DFS(x,a)
DFS(x,a) 表示当前在
x
x
x 节点,有流量
a
a
a,到终点
t
t
t 的最大流。当前弧优化在 DFS 里的关键点在 if(a==0) break;。
也就是说对于结点 x x x,如果 x x x 连接的前面一些弧已经能把 a a a 这么多的流量都送到终点,就不需要再去访问后面的一些弧了。当前未满的弧和后面未访问的弧等到下次再访问结点 x x x 的时候再去增广。
”
(附:本文段为CSDN博主「小小小小葱」的原创文章。原文链接)
2、拆点
是一种比较常用的、在解决某些最大流题目时的手段/方法。
就是把一个点拆成两个点(入点和出点),所有指向这个点的边都连向入点,而从这个点连出去的所有边的起点都在这个点的出点。
-
可以在入点和出点之间连单向边,容量设为 1。
若在入点和出点之间连边,就可以限制经过当前点的流量,如按上文所设,就只让一单位的流量经过当前点。
-
当然了,若是题目中看起来是一个整体的量实际上有多个小部分分别有不同的作用,也要拆点,但拆出来的点不一定要在之间连边。
拆点 相关题目:【LG-P2891】[USACO07OPEN]Dining G(题解)( double experience: \text{double experience: } double experience: P1402 酒店之王 | P1231 教辅的组成)
拆点 + 当前弧优化 相关题目:【LG - P2472 [SCOI2007]】蜥蜴(题解)( double experience: \text{double experience: } double experience: P3866 [TJOI2009] 战争游戏(题解))
二、最小割
最大流 = 最小割
将题目转化为求最小割,再将求最小割转化为求最大流。
求最小割方案
针对要求方案或是最小割中割去了哪些边的情况。
假如割完之后分成了两个部分——左部和右部。
那就可以逐一遍历右部点,查看它和左部点的反向连边的权值是否不为 0 ——最初建边的时候 自该右部点到该左部点这条反边 的权值设为了 0,
若是在增广过程中,有流 自该边的左部点流到右部点,即这条边被割去了,那么这条边的反边边权就会加上一个正数,所以以此就可以判断它的正边是否被割去。
例:P2763 试题库问题, P 2763 A C C o d e + N o t e s \mathfrak{P2763\ AC\ Code + Notes} P2763 AC Code+Notes
三、最小费用最大流
SPFA \text{SPFA} SPFA
从某种意义上来说,它和求最短路相似。所以直接用 spfa \text{spfa} spfa 就可以解决了。
代码 + 注释
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
#define int long long
#define rep(i, a, b) for(int i = a; i <= b; ++i)
const int maxn = 5e3 + 5;
const int maxm = 1e5 + 5;
int n, m, s, t;
bool vis[maxn];
int incf[maxn], dis[maxn], pre[maxn], mxfl, mxcs;
int cnt = 1, hd[maxn];
struct node{
int to, nxt, flw, cst;
}e[maxm];
inline void add(int u, int v, int w, int c)
{
e[++cnt].to = v;
e[cnt].nxt = hd[u], e[cnt].flw = w, e[cnt].cst = c;
hd[u] = cnt;
}
inline bool spfa()
{
queue <int> q;
memset(dis, 0x3f, sizeof dis);
memset(vis, 0, sizeof vis);
q.push(s), vis[s] = 1, dis[s] = 0, incf[s] = 2147483647;
while(!q.empty())
{
int u = q.front();
q.pop(), vis[u] = 0;
for(int i = hd[u], v; i; i = e[i].nxt)
{
if(!e[i].flw) continue;//注意不要漏掉
if(dis[v = e[i].to] > dis[u] + e[i].cst)
{
dis[v] = dis[u] + e[i].cst;//记录一路上的费用
incf[v] = min(incf[u], e[i].flw);//最终能流到 v点的流量
pre[v] = i;//记录路径
if(!vis[v]) vis[v] = 1, q.push(v);
}
}
}
if(dis[t] != dis[n + 2]) return true;
return false;
}
inline void mcmf()
{
while(spfa())//多次增广
{
mxfl += incf[t];
mxcs += incf[t] * dis[t];
int x = t, i;
while(x != s)
{
i = pre[x];
e[i].flw -= incf[t], e[i ^ 1].flw += incf[t];
x = e[i ^ 1].to;
}
}
}
signed main()
{
scanf("%lld %lld %lld %lld", &n, &m, &s, &t);
rep(i, 1, m)
{
int u, v, w, c;
scanf("%lld %lld %lld %lld", &u, &v, &w, &c);
add(u, v, w, c), add(v, u, 0, -c);
}
mcmf();
printf("%lld %lld\n", mxfl, mxcs);
return 0;
}
预流推进
这是一个解决最大流、时间最快、代码较长的算法。
算法详情及解法见:P4722 【模板】最大流 加强版 / 预流推进 题解—— by 531
HLPP \text{HLPP} HLPP 思路
按照众多大佬所说的那样, HLPP \text{HLPP} HLPP 就是将水流自源点一步一步地推到其他中转点,最后推向汇点,汇点累计的流量就是该网络的最大流。
注意,在此算法中,我们的目标是图中所有中转点最后存储的流量为 0。
在此过程中,为了防止 TLE \text{TLE} TLE,也就是避免两个点互相不停地将水流推来推去的情况,我们给每一个节点一个高度,像我们在 dinic \text{dinic} dinic 算法中所做的那样,每次保证是从当前层推向下一层。同时,也要保证每次从高度最高的节点向低处节点推流,节省时间(这也是使用优先队列的原因)。
那为什么它会比其他解决最大流问题的算法快呢?
首先,在这里我们只用运行一次 bfs \text{bfs} bfs,在给每一个节点初始了一个高度之后,后面如果它这个点储存的流传不出去了,也只需要针对它单独更改其高度即可。
其次,因为它是一步一步将流向下推,所以不用多次 dfs \text{dfs} dfs 去寻找增广路径。
整体代码:
#include<bits/stdc++.h>
using std::min;
using std::vector;
using std::queue;
using std::priority_queue;
#define maxn 2005
#define maxm 200005
#define inf 2147483647
#define rep(i, a, b) for(register int i = a; i <= b; ++i)
int n, m, s, t;
int cnt = 1, hd[maxn];
struct node{
int to, nxt, f;
}e[maxm << 1];
int p[maxn], h[maxn], gap[maxm];
bool inq[maxn];
queue <int> q;
struct cmp{
inline bool operator () (int a, int b) const//重写仿函数
{
return h[a] < h[b];
}
};
priority_queue <int, vector<int>, cmp> pq;
int u, v, w;
inline int read()
{
int x = 1, s = 0;
char ch = getchar();
while(ch < '0' or ch > '9') {if(ch == '-') x = -1; ch = getchar();}
while(ch >= '0' and ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return x * s;
}
inline void add(int u, int v, int w)
{
e[++cnt] = (node){v, hd[u], w};
hd[u] = cnt;
e[++cnt] = (node){u, hd[v], 0};
hd[v] = cnt;
}
inline bool bfs()
{
rep(i, 1, n) h[i] = inf;
h[t] = 0, q.push(t);
while(!q.empty())
{
int u = q.front();
q.pop();
for(int i = hd[u], v; i; i = e[i].nxt)
if(e[i ^ 1].f and h[v = e[i].to] > h[u] + 1)
h[v] = h[u] + 1, q.push(v);
}
return h[s] == inf ? 0 : 1;
}
inline void push(int nw)
{
for(int i = hd[nw], v; i; i = e[i].nxt)
{
if(!p[nw]) return;
if(h[v = e[i].to] + 1 != h[nw] or !e[i].f) continue;
int d = min(p[nw], e[i].f);
p[nw] -= d, p[v] += d, e[i].f -= d, e[i ^ 1].f += d;
if(v != s and v != t and !inq[v])
pq.push(v), inq[v] = 1;
}
}
inline void updt(int u)
{
h[u] = inf;
for(int i = hd[u], v; i; i = e[i].nxt)
{
if(e[i].f and h[v = e[i].to] + 1 < h[u])
h[u] = h[v] + 1;
}
}
inline int hlpp()
{
if(!bfs()) return 0;
h[s] = n;
for(int i = hd[s], v, d; i; i = e[i].nxt)
{
if(d = e[i].f)
{
p[v = e[i].to] += d, p[s] -= d;
e[i].f -= d, e[i ^ 1].f += d;
if(v != s and v != t and !inq[v]) pq.push(v), inq[v] = 1;
}
}
rep(i, 1, n) if(h[i] != inf) gap[h[i]] += 1;
while(!pq.empty())
{
int u = pq.top();
pq.pop(), inq[u] = 0, push(u);
if(!p[u]) continue;
if(!--gap[h[u]])
{
rep(i, 1, n)
if(i != s and i != t and h[i] > h[u] and h[i] < n + 1)
h[i] = n + 1;
}
updt(u), gap[h[u]] += 1, pq.push(u), inq[u] = 1;
}
return p[t];
}
int main()
{
n = read(), m = read(), s = read(), t = read();
rep(i, 1, m)
u = read(), v = read(), w = read(), add(u, v, w);
printf("%d\n", hlpp());
return 0;
}
1、分层图
一些题目中,在原来单纯网络流的基础上又加了一个状态,这时就得再用分层图了。
一道分层图类型很好的例题。分层后可以使用最短路 spfa \text{spfa} spfa,也可以用最小费用最大流解决。
回到题目。如果没有油量的限制,很明显就是一道费用流。但是在有了油量的限制之后,车到达每一个节点时的状态(即当时剩余的油量)就不同,就不能将它们归为一个点处理。
所以,在油量上限为 k k k 时,我们将图分为 ( k + 1 ) (k+1) (k+1) 层,第 i i i 层的图中的节点 ( x , y ) (x,y) (x,y) 表示汽车在 ( x , y ) (x,y) (x,y) 这个节点时油量为 ( k − i ) (k-i) (k−i)。所以第 0 层代表满油。
有了这个基础理解之后,剩下的建边根据题意即可。
此题 AC \text{AC} AC 代码及注释如下:
注意数组边界大小;此处没有放最小费用流板子,只放了建边过程。
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(int i = a; i <= b; ++i)
#define maxn 110005
#define maxm 1100100
#define inf 2147483647
const int c = 10000;
int n, K, A, B, C;
int cnt = 1, hd[maxn];
struct node{
int to, nxt, flw, cst;
}e[maxm];
int s, t = maxn - 1;
int dis[maxn];
bool vis[maxn];
int incf[maxn];
int pre[maxn];
inline void add(int u, int v, int f, int c)
{
e[++cnt] = (node){v, hd[u], f, c};
hd[u] = cnt;
e[++cnt] = (node){u, hd[v], 0, -c};
hd[v] = cnt;
}
inline int id(int i, int j)
{
return (i - 1) * n + j;
}
int main()
{
scanf("%d %d %d %d %d", &n, &K, &A, &B, &C);
add(s, id(1, 1)/*起始点,此时汽车为满油,所以在第 0 层*/, 1, 0);
rep(i, 0, K) add(id(n, n) + c * i/*每一层的终点。只要到了终点不论在哪一层都可以结束*/, t, 1, 0);
rep(i, 1, n) rep(j, 1, n)
{
int tmp;
scanf("%d", &tmp);
if(tmp)//如果有油箱
rep(k, 1, K) add(id(i, j) + c * k/*每碰到油箱都要强制加油,回到第 0 层*/, id(i, j), 1, A);
rep(k, 0, K - 1)
{
if(tmp/*油箱*/ and k/*因为强制性加油,所以最后都会回到第 0 层,上面都不考虑*/) break;
if(i + 1 <= n) add(id(i, j) + c * k, id(i + 1, j) + (k + 1) * c/*因为每走一步都在减少油量,所以要向上层连边*/, 1, 0);
if(j + 1 <= n) add(id(i, j) + c * k, id(i, j + 1) + (k + 1) * c, 1, 0);
if(i - 1 >= 1) add(id(i, j) + c * k, id(i - 1, j) + (k + 1) * c, 1, B);
if(j - 1 >= 1) add(id(i, j) + c * k, id(i, j - 1) + (k + 1) * c, 1, B);
}
add(id(i, j) + K * c, id(i, j), 1, A + C);//新建一个油箱并加满油回到第 0 层
}
printf("%d\n", mcmf());
return 0;
}
四、最大权闭合子图
1. 概念
-
闭合子图:在原图 G G G 的闭合子图中,每一个节点,它在 G G G 中所能到达的所有节点都包含在这个子图中。
-
最大权闭合子图:即原图 G G G 中点权之和最大的闭合子图。
2. 运用
目标:求一图的最大权闭合子图。
<1>
先建立一超级源点和超级汇点。
对于每个带权值的节点:
- 若节点为正,则与超级源点相连,流量为该点权值;
- 反之,则与超级汇点相连,流量为该点权值相反数。
很明显,在不考虑“每个点在 G G G 中所能到达的所有节点都包含在这个子图中”这个限制条件时,最大权“闭合子图”肯定是所有正权值之和,也就是现在与源点相连的所有边流量之和。
此时,上述的建边方式的原因就清楚明了了:区分开来正负权值的点。
<2>
然后再加上限制,在点和点之间建边。
此时可以隐约发现:我们会使用最小割去求出最大权子图。
割去一些边,使源点与汇点不相连,最后源点所在的那个子图即为原图的最大权闭合子图。
回过头来:这些边的流量是什么?
这些边的流量为 i n f inf inf。因为“每个点在 G G G 中所能到达的所有节点都包含在这个子图中”,所以要保证这些边不会被割去。
<3>
此时可以发现,被割去的边都是与源点或者汇点相连的边。
-
若一负权值节点与汇点相连的边被割去:
说明此时它放在最大权闭合子图中是最优的状态,但最大权闭合子图的权值和要减去该点权值的绝对值。
-
若一正权值节点与汇点相连的边被割去:
说明此时它不放在最大权闭合子图中是最优的状态,但最大权闭合子图的权值和要减去该点权值。
这样一来,最大权闭合子图的权值和就是:正权值之和 - 最小割。
然后最小割转化为最大流去求解即可。
例题:P2805 [NOI2009] 植物大战僵尸 | P3872 [TJOI2010]电影迷(题解)
五、经典例题
【Luogu-P3324 [SDOI2015] / DSY-1993】星际战争(题解)
—— E n d \mathfrak{End} End——




 浙公网安备 33010602011771号
浙公网安备 33010602011771号