ZR2025 dp

CF1606E Arena

竞技场中有 \(n\) 个英雄正在战斗。最初，第 \(i\) 个英雄拥有 \(a_i\) 点生命值。
战斗分为若干回合进行。在每一回合开始时，每个存活的英雄会对其他所有英雄各造成 \(1\) 点伤害。所有英雄的攻击是同时发生的。在一回合结束后，生命值小于 \(1\) 的英雄被视为阵亡。
如果在某一回合结束后，恰好只剩下 \(1\) 个英雄存活，那么他将被宣布为胜者。否则，比赛没有胜者。
你的任务是计算有多少种方式为每个英雄选择初始生命值 \(a_i\)，其中 \(1 \le a_i \le x\)，使得比赛没有胜者。由于方案数可能非常大，请输出对 \(998244353\) 取模后的结果。如果至少有一个英雄的生命值不同，则两种方案被视为不同。例如，\([1, 2, 1]\) 和 \([2, 1, 1]\) 是不同的。
\(2 \le n \le 500; 1 \le x \le 500\)

首先发现一个需要关心的条件是当前人数，因为它决定血减多少，然后显然剩下的就要限制人的血量了，发现设成 \(\leq x\) 是不好的，这样不知道下一轮死几个人，于是设成最大血量恰好为 \(x\)，转移分 \(i,j\) 大小看一下，如果一轮死不光就枚举这一轮死几个即可。

最终状态：\(f_{i,j}\) 表示 \(i\) 个人，最大血量恰好为 \(j\) 的合法局面方案数。

CF1716C Robot in a Hallway

有一 \(2\) 行 \(m\) 列的网格，从上到下编号为 \(1\) 至 \(2\)，从左往右编号为 \(1\) 至 \(m\)。
机器人开始时在网格 \((1,1)\) 内。一秒内，它可以进行如下任意一个动作：

• 走到上、下、左、右任意相邻的网格
• 待在网格内不动

开始时，除了网格 \((1,1)\) 其他格子都是锁着的。每个网格 \((i,j)\) 有一个值 \(a_{i,j}\)，表示该网格解锁的时间。只有经过至少 \(a_{i,j}\) 秒后，机器人才可以进入网格 \((i,j)\)。
机器人要走遍所有网格，且每个网格只能被访问一次（网格 \((1,1)\) 在一开始就被访问过）。访问可以在任意网格内结束。
实现如上操作的最快时间是什么？
$ 2 \le m \le 2 \cdot 10^5 $

观察答案的形态，一定是一段蛇形再拼上一段先走出去再绕回来的路。前面的蛇形直接走算一下就行，后面的 dp 一下就行。

CF1716D Chip Move

在数轴上有一个棋子。初始时，棋子位于点 \(0\)。你可以进行任意次数的移动；每次移动会使棋子的坐标增加某个正整数（称为这次移动的长度）。第一次移动的长度必须能被 \(k\) 整除，第二次移动的长度必须能被 \(k+1\) 整除，第三次移动的长度必须能被 \(k+2\) 整除，依此类推。
例如，如果 \(k=2\)，则移动序列可能如下：\(0 \rightarrow 4 \rightarrow 7 \rightarrow 19 \rightarrow 44\)，因为 \(4-0=4\) 能被 \(2=k\) 整除，\(7-4=3\) 能被 \(3=k+1\) 整除，\(19-7=12\) 能被 \(4=k+2\) 整除，\(44-19=25\) 能被 \(5=k+3\) 整除。
给定两个正整数 \(n\) 和 \(k\)。你的任务是，对于每个 \(x \in [1, n]\)，计算从 \(0\) 出发到达点 \(x\) 的方案数。方案数可能非常大，请对 \(998244353\) 取模输出。若两种方案经过的位置集合不同，则认为它们是不同的方案。
\(1 \le k \le n \le 2 \cdot 10^5\)

显然最多跳 \(\sqrt{n}\) 步，直接 dp 就做完了。

P3574 [POI 2014] FAR-FarmCraft

在一个叫做比特村的小村庄中，有 \(n-1\) 条路连接着这个村庄中的全部 \(n\) 个房子。
每两个房子之间都有一条唯一的通路。这些房子的编号为 \(1\) 至 \(n\)。
\(1\) 号房子属于村庄的管理员比特安萨尔。
为了提升村庄的科技使用水平，\(n\) 台电脑被快递到了比特安萨尔的房子。每个房子都应该有一台电脑，且分发电脑的任务就落在了比特安萨尔的肩上。
比特村的居民一致同意去玩农场物语这个游戏的最新快照版，而且好消息是他们很快就要得到他们最新的高配置电脑了。
比特安萨尔将所有电脑都装在了他的卡车上，而且他准备好完成这个艰巨的任务了。
他的汽油恰好够走每条路两遍。
在每个房子边，比特安萨尔把电脑贴心的配送给居民，且立即前往下一个房子。（配送过程不花费任何时间）
只要每间房子的居民拿到了他们的新电脑，它们就会立即开始安装农场物语。安装农场物语所用的时间根据居民的科技素养而定。幸运的是，每间房子中居民的科技素养都是已知的。
在比特安萨尔配送完所有电脑后，他会回到他自己的 \(1\) 号房子去安装他自己的农场物语。
用卡车开过每条路的时间恰好是 \(1\) 分钟，而居民开电脑箱的时间可以忽略不计。（因为他们太想玩农场物语了）
请你帮助比特安萨尔算出从开始配送到所有居民都玩上了农场物语的最少时间。
\(2 \leq n \leq 5\times 10^5\)

令 \(f_x\) 表示 \(x\) 子树的答案，转移就是要决策走每个儿子子树的顺序，显然走完一个子树出来用的时间是固定的，是 \(2(sz-1)\)，用贪心邻项交换可分析得按 \(f_x-2(sz-1)\) 从大到小走。

CF1748E Yet Another Array Counting Problem

对于长度为 \(n\) 的序列 \(x\)，定义其在子段 \([l;r]\) 的“最左端最大值位置”为最小的满足 \(l\leq i\leq r\) 且 \(x_i=\max_{j=l}^rx_j\) 的整数 \(i\)。
给定整数 \(n,m\) 和长度为 \(n\) 的序列 \(a\)，你需要求出满足下列要求的序列 \(b\) 的数量：

• 序列 \(b\) 长度为 \(n\)，且对任意整数 \(i(1\leq i\leq n)\) 都有 \(1\leq b_i\leq m\) 成立。
• 对任意整数 \(l,r(1\leq l\leq r\leq n)\)，总有 \(a,b\) 在子段 \([l;r]\) 的“最左端最大值位置”相同。

答案对 \(10^9+7\) 取模。
\(n,m(2\leq n,m\leq2\times10^5;\sum n\times m\leq10^6)\)

题目的条件相当于对数组建出来笛卡尔树形态相同，所以就对 \(a\) 建一下，然后在树上 dp 即可，可以发现只用记录下根的权就行，\(f_{i,j}\) 表示 \(i\) 的子树内，\(b_i=j\)，子树内的方案数，转移就枚举左右儿子怎么取，两边乘起来就行。

CF1830D Mex Tree

给定一棵有 \(n\) 个节点的树。对于每个节点，你可以将其染成 \(0\) 或 \(1\)。
一条路径 \((u,v)\) 的价值等于从 \(u\) 到 \(v\) 的最短路径上所有节点的颜色的 MEX \(^\dagger\)。
一次染色的价值等于所有满足 \(1 \leq u \leq v \leq n\) 的路径 \((u,v)\) 的价值之和。
请问该树的任意染色方案中，最大可能的价值是多少？
\(1 \leq n \leq 2 \cdot 10^5\)

首先考虑怎么刻画 MEX，注意到权只有 0,1 两种，意味着 mex 也只有 0,1,2 三种。具体的同色 0 连通块内点对是 1，同色 1 是 0，其它是 2。

发现关系的是连通快大小的信息，用经典 dp：\(f_{i,j,0/1}\) 表示 \(i\) 子树内，\(i\) 所在连通块大小为 \(j\)，所在连通块是 \(0/1\) 同色块，转移用类似背包的方式合并即可。

这样是 \(O(n^2)\) 的。再进一步的，考虑给树按照深度的奇偶性 0,1 交替染色，此时答案比最优解少 \(O(n)\)，所以连通块大小是 \(O(\sqrt{n})\) 的，可以通过。

CF1725J Journey

给定一棵带权树，走一条边的时间是它的边权，你可以从任意点开始游走，每次走到相邻节点，你需要走过所有城市。在过程中你可以瞬移一次，即不话费任何时间移动到任意一个城市继续游走。问需要花费的最小时间。\(n \leq 10^5\)。

首先考虑无法瞬移的情况，答案就是 \(2sumE-d\)，\(d\) 为树的直径长度，\(sumE\) 为所有边权之和。

我们加上瞬移，我们发现瞬移前后经过的点和边都构成树，那么假设前后分别是 \(T_1,T_2\)，那么答案就是要对于所有 \(V(T_1)+V(T_2)=V(T)\) 的 \(T_1,T_2\) 求 \(sumE(T_1)+sumE(T_2)-d(T_1)-d(T_2)\) 的最小值，\(d(T)\) 表示树 \(T\) 的直径。

考虑这两条直径是什么，分下面三种形态：

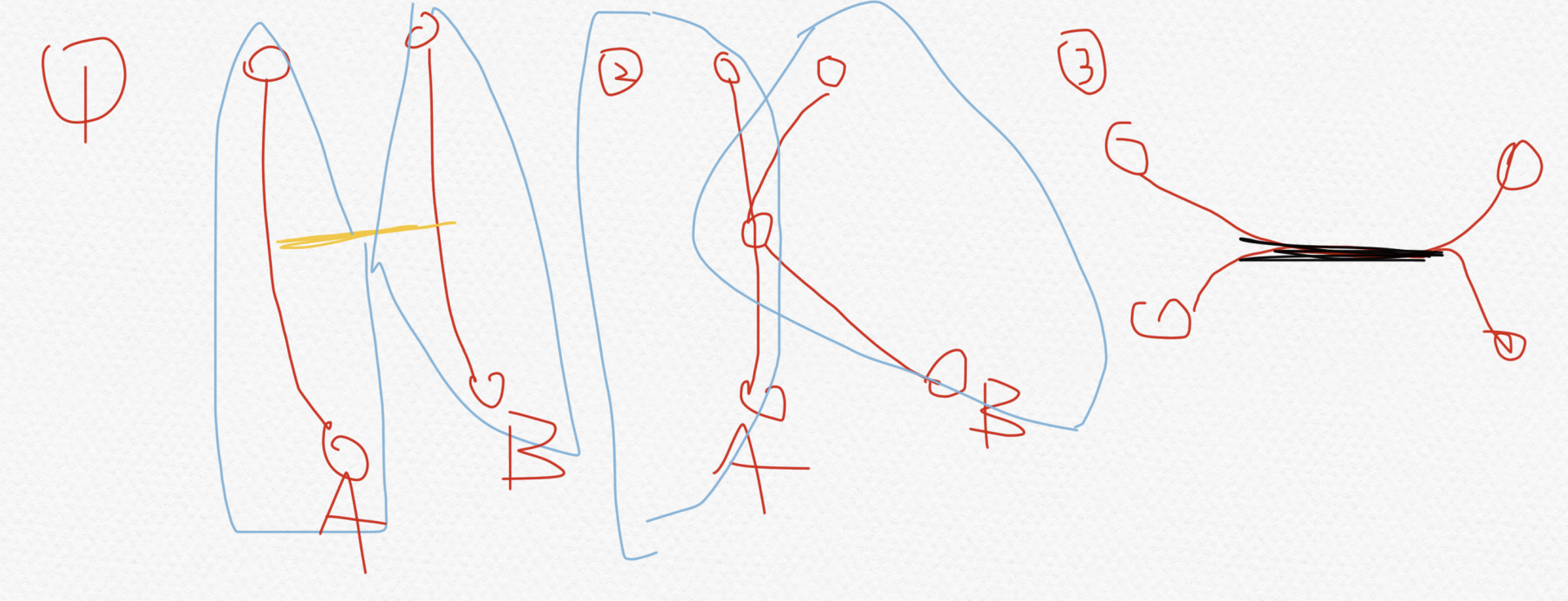
蓝色圈表示树的划分，黄色表示连接两个链的一串边，黑色表示两条链的边交。

第一种是无交，第二种是点交，第三种是边交（这一种显然不优，替换成左边一条，右边一条不劣）。

所以简单讨论一下即可。

直径信息不难用换根处理。