whk 笔记

开的坑，自用，因为我学的比较散，所以进度肯定是不快的。

Leq 解题策略

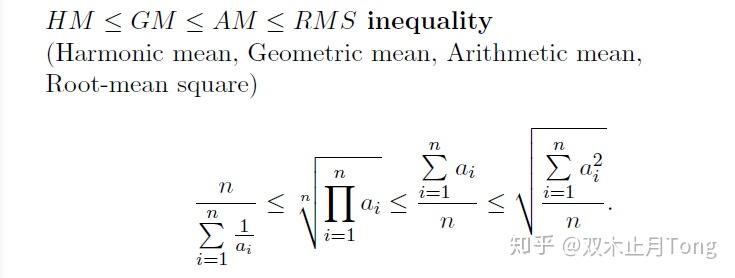
常用的是 \(a_1+a_2+...+a_n \geq n\sqrt[n]{a_1a_2...a_n}\)。

首先 Leq 的题肯定得有一步用到 Leq，从而得到一个不等式关系，这个不等式关系往往直接或间接的帮助我们证明不等式。那么我手玩了一下觉得是有下面的框架的：

定义下面的流程为一个 part:

1. 凑出 Leq 形式
2. 使用 Leq

那么整个解题流程就是由基本代数变形来连接一些 part，这个代数变形包括内部的变形和放缩。

如果题目里面有关于变量的条件，那么我们在变形和凑形式的时候也往往可以尝试使用这些条件。

比如有一个等式条件 \(a+2b=2\)，那么就有一些可能的手法：

• \(a=2-2b\)
• \(\frac{1}{2} \times (a+2b) \times A\)，其中 \(A\) 是需要被配凑的多项式
• ...

有一些题：

已知 \(a,b,c>0,abc=1\)，求证 \(a^2+b^2+c^2 \geq \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)。

三元，直接把条件代没有什么性质，因为不等式是轮换的，然而代的话不仅破坏这个结构，并且也没有任何性质，肯定不能直接代。

根据常见手法第二条，把不等式右边乘 \(abc\)，也就是 \(a^2+b^2+c^2 \geq ab+ac+bc\)，两边乘 \(2\) 得 \(2a^2+2b^2+2c^2 \geq 2(ab+ac+bc)\)，又有 \(a^2+b^2 \geq 2ab,a^2+c^2 \geq 2ac,b^2+c^2 \geq 2bc\)，相加即证。

收获：

如果条件和证明的不等式都很对称，那么往往在解题过程中不管如何变形始终保证对称形式。
\((a+b)+(a+c)+(b+c)=2(a+b+c)\)。
配凑是有目的性的。
倒数之和可以写成 \(\frac{a_2a_3...a_n+a_1a_3...a_n+...+a_1a_2...a_{n-1}}{a_1a_2...a_n}\)。