根据先序遍历和中序遍历生成后序遍历
根据先序遍历和中序遍历生成后序遍历
作者:Grey
原文地址:
问题描述
思路
假设有一棵二叉树
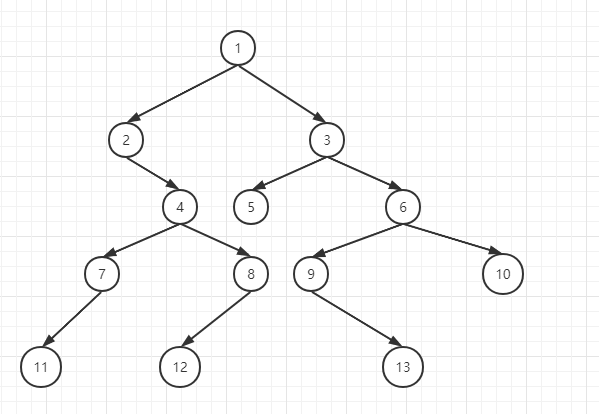
先序遍历的结果是

中序遍历的结果是

由于先序遍历大的调度逻辑是,先头,再左,再右
后序遍历的调度逻辑是:先左,再右,再头。
所以:后序遍历的最后一个节点,一定是先序遍历的头节点。
定义递归函数
// 先序遍历数组pre的[l1...r1]区间
// 中序遍历数组in的[l2...r2]区间
// 生成后序遍历数组pos的[l3...r3]区间
void func(int[] pre, int l1, int r1, int[] in, int l2, int r2, int[] pos, int l3, r3)
依据以上推断,可以得到如下结论
// 后序遍历的最后一个节点,一定是先序遍历的头节点
pos[r3] = pre[l1];
然后,在中序数组中,我们可以定位到这个头节点的位置,即下图中标黄的位置,假设这个位置是index,

这个index将中序数组分成了左右两个部分,由于中序遍历的调度过程是:先左,再头,再右,所以在中序遍历中[l2......index]区间内,是以index位置为头的左树中序遍历结果,[l2......index]区间内元素个数假设为b,那么在先序遍历中,从头往后数b个元素,即:[l1......l1+b]构成了以index位置为头的左树的先序遍历结果。
public static void func(int[] pre, int l1, int r1, int[] in, int l2, int r2, int[] pos, int l3, int r3) {
if (l1 > r1) {
// 避免了无效情况
return;
}
if (l1 == r1) {
// 只有一个数的时候
pos[l3] = pre[l1];
} else {
// 不止一个数的时候
pos[r3] = pre[l1];
// index表示某个头在中序数组中的位置
int index;
// 可以优化
for (index = l2; index <= r2; index++) {
if (in[index] == pre[l1]) {
break;
}
}
int b = index - l2;
func(pre, l1 + 1, l1 + b, in, l2, index - 1, pos, l3, l3 + b - 1);
func(pre, l1 + b + 1, r1, in, index + 1, r2, pos, l3 + b, r3 - 1);
}
}
优化
在递归函数func中,有一个遍历的行为,
for (index = l2; index <= r2; index++) {
if (in[index] == pre[l1]) {
break;
}
}
如果每次递归都要遍历一下,那么效率会降低,所以可以在一开始就设置一个map,存一下中序遍历中每个值所在的位置信息,这样就不需要通过遍历来找位置了,方法如下:
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
inOrder[i] = in.nextInt();
map.put(inOrder[i], i);
}
这样预处理以后,每次index的位置不需要遍历得到,只需要
int index = map.get(pre[l1]);
即可,完整代码见
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] preOrder = new int[n];
int[] inOrder = new int[n];
for (int i = 0; i < n; i++) {
preOrder[i] = in.nextInt();
}
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
inOrder[i] = in.nextInt();
map.put(inOrder[i], i);
}
int[] posOrder = new int[n];
func(preOrder, 0, n - 1, inOrder, 0, n - 1, posOrder, 0, n - 1, map);
for (int i = 0; i < n; i++) {
System.out.print(posOrder[i] + " ");
}
in.close();
}
public static void func(int[] pre, int l1, int r1, int[] in, int l2, int r2, int[] pos, int l3, int r3, Map<Integer, Integer> map) {
if (l1 > r1) {
// 避免了无效情况
return;
}
if (l1 == r1) {
// 只有一个数的时候
pos[l3] = pre[l1];
} else {
// 不止一个数的时候
pos[r3] = pre[l1];
// index表示某个头在中序数组中的位置
int index = map.get(pre[l1]);
int b = index - l2;
func(pre, l1 + 1, l1 + b, in, l2, index - 1, pos, l3, l3 + b - 1, map);
func(pre, l1 + b + 1, r1, in, index + 1, r2, pos, l3 + b, r3 - 1, map);
}
}
}
更多
本文来自博客园,作者:Grey Zeng,转载请注明原文链接:https://www.cnblogs.com/greyzeng/p/16406847.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号