力扣 leetcode 1742. 盒子中小球的最大数量

题目描述

你在一家生产小球的玩具厂工作，有 n 个小球，编号从 lowLimit 开始，到 highLimit 结束（包括 lowLimit 和 highLimit ，即 n == highLimit - lowLimit + 1 ）。另有无限数量的盒子，编号从 1 到 infinity 。

你的工作是将每个小球放入盒子中，其中盒子的编号应当等于小球编号上每位数字的和。例如，编号 321 的小球应当放入编号 3 + 2 + 1 = 6 的盒子，而编号 10 的小球应当放入编号 1 + 0 = 1 的盒子。

给你两个整数 lowLimit 和 highLimit ，返回放有最多小球的盒子中的小球数量。如果有多个盒子都满足放有最多小球，只需返回其中任一盒子的小球数量。

提示：1 <= lowLimit <= highLimit <= 10^5

示例

示例1：

输入： lowLimit = 1, highLimit = 10
输出： 2
解释：
盒子编号：1 2 3 4 5 6 7 8 9 10 11 ...
小球数量：2 1 1 1 1 1 1 1 1 0  0 ...  
编号 1 的盒子放有最多小球，小球数量为 2 。

示例2：

输入：lowLimit = 5, highLimit = 15
输出：2
解释：
盒子编号：1 2 3 4 5 6 7 8 9 10 11 ...
小球数量：1 1 1 1 2 2 1 1 1 0  0  ...
编号 5 和 6 的盒子放有最多小球，每个盒子中的小球数量都是 2 。

示例 3：

输入：lowLimit = 19, highLimit = 28
输出：2
解释：
盒子编号：1 2 3 4 5 6 7 8 9 10 11 12 ...
小球数量：0 1 1 1 1 1 1 1 1 2  0  0  ...
编号 10 的盒子放有最多小球，小球数量为 2 。

解题思路

根据题意，将小球从1开始编号，然后可以发现在1 <= lowLimit <= highLimit <= 10^5时，球的编号是99999时盒子编号最大，为45=9+9+9+9+9。因此，可以用一个长度为45的数组保存每个盒子中小球的个数，然后再根据小球编号计算小球应该放在哪个盒子：

int box_id = 0;
while(num){
    box_id += num % 10;
    num /= 10;
}

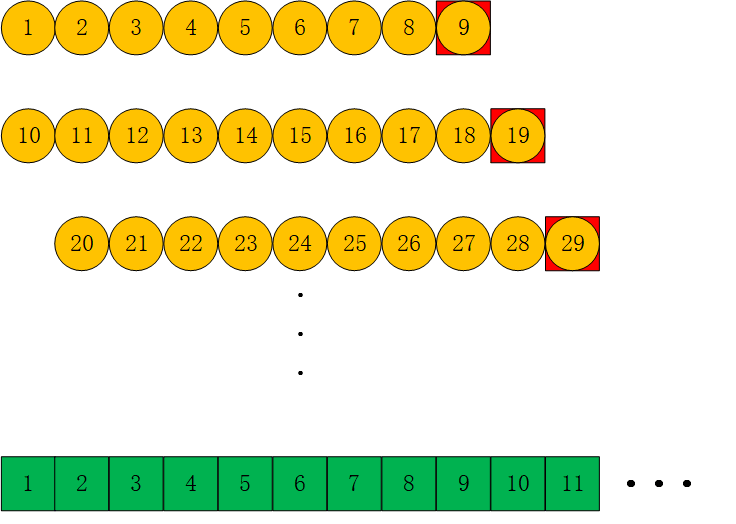
除此之外，小球的所放盒子也存在一定规律。从上图中可以看出，我们就可以只针对末尾是9的小球进行特殊定位计算，而其他小球所在的位置，只需要根据前面小球位置+1即可。例如，当小球编号最后一位为 9 时，下一个小球将放在新的位置，继续开始循环。观察其中规律可以发现，假设小球A编号的尾号为9，则下一个小球B=A+1所在的箱子为：B球所在编号=A球所在编号-（9*A球末尾9的个数）+1。此时，小球所放盒子编号的计算方法为：

for (int i = lowLimit; i < highLimit; i++) {
    for (int j = i; j % 10 == 9; j /= 10){ // 根据前一个数的末位是否为9，来重新定位下一个数的位置
        firstIndex -= 9; // 前移9位
     }
    box[++firstIndex]++;
}

最后，将box中的最大值输出即可。