样条曲线

C0连续，C1连续，C2连续

C0连续，函数连续
C1连续，一阶导连续
C2连续，二阶导连续

多项式插值

n个点可用n-1阶多项式确定一条曲线。

贝塞尔曲线

https://zh.wikipedia.org/zh-cn/貝茲曲線

深入了解贝塞尔曲线

控制点不一定要在曲线上，仅端点(起点和终点)在曲线上。

两个点：线段

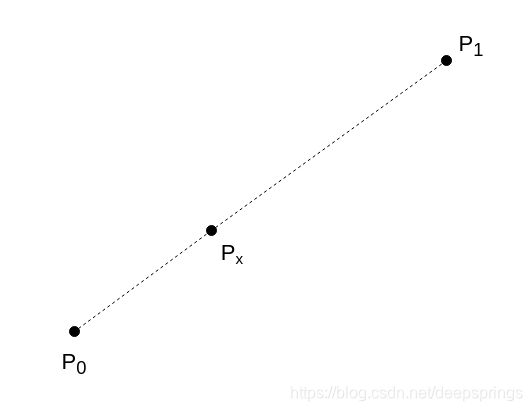
\[\mathrm{P_x=P_0+(P_1-P_0)t=(1-t)P_0+tP_1,\quad t\in[0,1]} \]

三个点：抛物线三切线定理

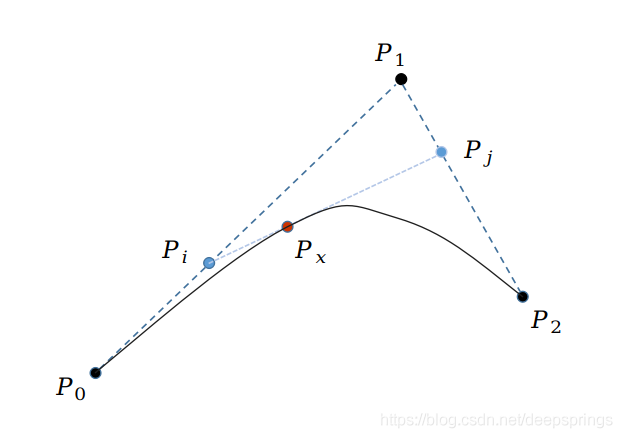
\[\mathrm{P_x~=(1-t)P_i~+tP_j~=(1-t)[(1-t)P_0~+tP_1~]+t[(1-t)P_1~+tP_2~]=(1-t)^2P_0~+2t(1-t)P_1~+t^2P_2} \]

一般化，n个点

n阶贝塞尔曲线：

\[\mathbf{B}(t)=\sum_{i=0}^n\binom ni\mathbf{P}_i(1-t)^{n-i}t^i=\binom n0\mathbf{P}_0(1-t)^nt^0+\binom n1\mathbf{P}_1(1-t)^{n-1}t^1+\cdots+\binom n{n-1}\mathbf{P}_{n-1}(1-t)^1t^{n-1}+\binom nn\mathbf{P}_n(1-t)^0t^n,t\in[0,1] \]

即，

\[\mathbf{B}(t)=\sum_{i=0}^n\mathbf{P}_i\mathbf{b}_{i,n}(t),\quad t\in[0,1] \]

\[\mathbf{b}_{i,n}(t)=\binom nit^i(1-t)^{n-i},\quad i=0,\ldots n \]

\(\mathbf{b}_{i,n}(t)\)又叫做伯恩斯坦基底多项式，\(\mathbf{P}_i\)为控制点。

即t决定权重，n个控制点加权后得到插值点。

B样条曲线

B --> B样条基。

节点：分段的作用。均匀划分就是均匀B样条曲线。

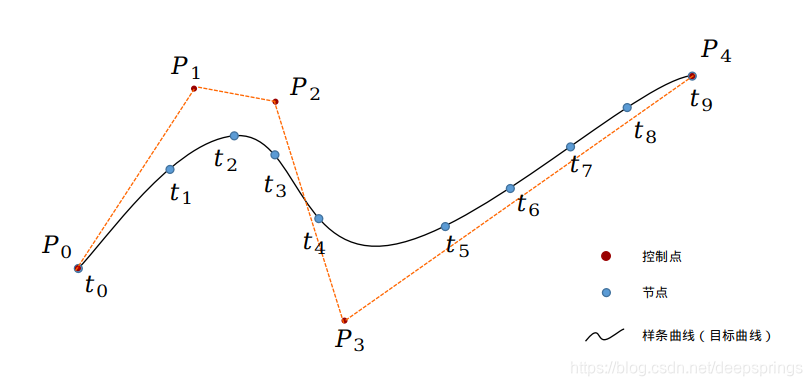
n+1=5个控制点：\(P_i\)，m+1=10个节点：\(t_i\)，k=m-n-1=3次。
公式为，由n次B样条基组成：

\[\mathrm{P(t)}=\sum_{i=0}^{n} B_{i,k}(t) P_i \]

\[ \begin{gathered} \left.\mathrm k=0,\quad\mathrm B_{\mathrm i,0}(\mathrm t)=\left\{\begin{matrix}1,&\text{ t [t i,t i +1]}\\0,&\text{ Otherwise}\end{matrix}\right.\right. \\ \mathrm{k>0,~B_{i,k}\left(t\right)=\frac{t-t_i}{t_{i+k}-t_i}B_{i,k-1}\left(t\right)+\frac{t_{i+k+1}-t}{t_{i+k+1}-t_{i+1}}B_{i+1,k-1}\left(t\right)} \end{gathered} \]