最大流最小割定理

先来理解几个概念

割

在原先能够流通的网络中移除的边集，使得网络无法流通

最小割

所有的割中边权和最小的割即为最小割

可以想象一下，Kido为了自给自足给自己建了超多供水管道（kido能进行光合作用），形成了一个网络，然后容量越大的管道防护设施越好，但是总有人想渴死Kido就想炸掉管道，但是贫乏的恐怖分子既想渴死kido又想节约成本，那么最节约成本的破坏管道的方案即为最小割

 

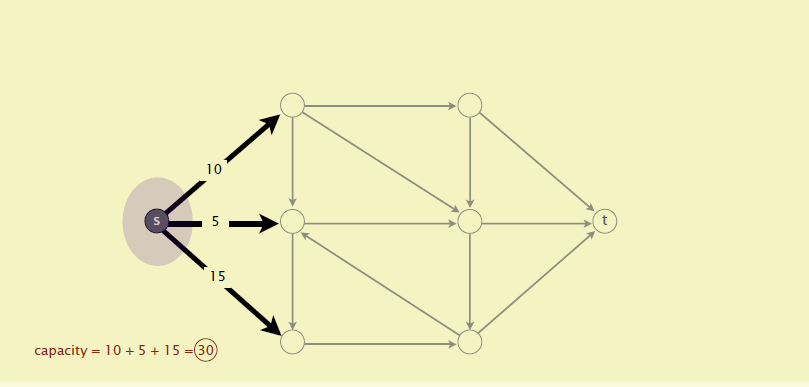
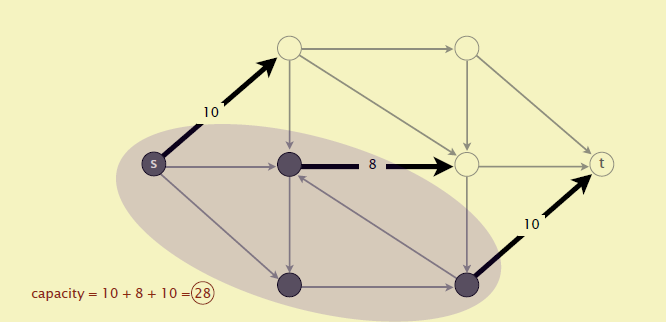
 最大流最小割定理

在任何的网络中，最大流的值等于最小割的容量

具体的证明分三部分

1.任意一个流都小于等于任意一个割
这个很好理解 自来水公司随便给你家通点水，构成一个流
恐怖分子随便砍几刀 砍出一个割
由于容量限制，每一根的被砍的水管子流出的水流量都小于管子的容量
每一根被砍的水管的水本来都要到你家的，现在流到外面 加起来得到的流量还是等于原来的流
管子的容量加起来就是割，所以流小于等于割
由于上面的流和割都是任意构造的，所以任意一个流小于任意一个割

2.构造出一个流等于一个割
当达到最大流时，根据增广路定理
残留网络中s到t已经没有通路了，否则还能继续增广
我们把s能到的的点集设为S,不能到的点集为T
构造出一个割集C[S,T],S到T的边必然满流 否则就能继续增广
这些满流边的流量和就是当前的流即最大流
把这些满流边作为割，就构造出了一个和最大流相等的割

相当于在残量网络中，源点能到达的结点的各个边的容量和为最大流

所以如果我们要求一个最小割的边集，我们只要跑一编最大流，然后在残量网络中找正向边残量为0的边，那么这条边肯定在最小割里面，这样就可以得到一组最小割的边集

3.最大流等于最小割
设相等的流和割分别为Fm和Cm
则因为任意一个流小于等于任意一个割

任意F≤Fm=Cm≤任意C

定理说明完成，证明如下：

对于一个网络流图G=(V,E) G=(V,E)G=(V,E)，其中有源点s和汇点t，那么下面三个条件是等价的：

1.流f是图G的最大流
2.残留网络Gf不存在增广路
3.对于G的某一个割(S,T)，此时f=C(S,T) 
首先证明1 => 2：

我们利用反证法，假设流f是图G的最大流，但是残留网络中还存在有增广路p，其流量为fp。则我们有流f′=f+fp>f 。这与f是最大流产生矛盾。

接着证明2 => 3：

假设残留网络Gf不存在增广路，所以在残留网络Gf中不存在路径从s到达t。我们定义S集合为：当前残留网络中s能够到达的点。同时定义T=V-S。
此时(S,T)构成一个割(S,T)。且对于任意的u∈S,v∈T ，有f(u,v)=c(u,v)。若f(u,v)=c(u,v) 。若c(u,v)f(u,v)<c(u,v)，则有Gf(u,v)>0，s可以到达v，与v属于T矛盾。
因此有f(S,T)=Σf(u,v)=Σc(u,v)=C(S,T)。

最后证明3 => 1：

由于f的上界为最小割，当f到达割的容量时，显然就已经到达最大值，因此f为最大流。

这样就说明了为什么找不到增广路时，所求得的一定是最大流。