DGP - 2. Discrete differential geometry

DGP - 2. Discrete differential geometry

视屏地址：https://www.bilibili.com/video/BV1B54y1B7Uc

目标

为了获取三角网格表面近似的微分特性。

• 局部平均区域；
• 法向量；
• 梯度；
• 拉普拉斯算子；
• 离散曲率；

局部平均区域

人与人之间是存在安全距离的，在一个食堂，面对周围都是不熟悉的人，一般都会选择和别人不相邻的位置进餐。三角网格表面中的一个点，它的局部平均区域是怎么样的呢？

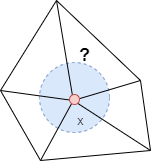
通常有三种表示方法：

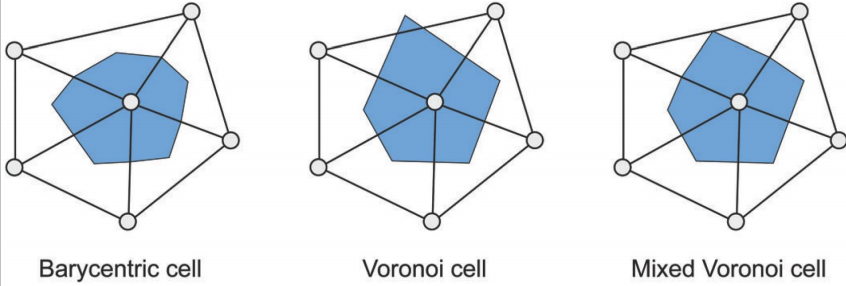
• Barycentric cell：将顶点周围的三角面的重心坐标连接到一起；
• Voronoi cell：泰森多边形，又叫洛诺伊图，顶点周围线段的垂直平分线组成的区域；
• Mixed Voronoi cell：利用对边的中心点对Voronoi cell的修正，防止连接线超出周围三角形区域；

各自的面积计算如下：

Barycentric cell：其面积为周围三角形面积之和的三分之一；

Voronoi cell：三角形外切圆半径计算链接，根据外切圆半径可以计算得到周围区域的面积；

Mixed Voronoi cell：修正的区域面积为三角形面积的一般，非修正区域的面积计算和Voronoi cell一致。

法向量

三角形的法向量是很明确的，通过叉积就能够计算得到。但是一个顶点的法向量是怎么确定呢？通常是通过该顶点的one-ring邻域计算得到的，如下：

\[n(v) = \frac{\sum_{T\in \Omega (v)} \alpha_T \bold{n}(T)}{||\sum_{T\in \Omega(v)}\alpha_T\bold{n}(T)||_2} \]

其中，\(T\)为领域的三角形，\(\bold{n}(T)\)为三角形的法向量，\(\alpha(T)\)为权重，权重的取值通常有：

• 常量，取值为1；
• 三角形面积；
• 三角形与该顶点关联的角度；

三角形内点的梯度

三角形内的点(x)可以用重心坐标，结合三角形的三个点(xi, xj, xk)进行表示：

\[x = \alpha x_i + \beta x_j + \gamma x_k \]

那么x点的梯度就可以写成：

\[\bigtriangledown_x x = x_i \bigtriangledown_x \alpha + x_j \bigtriangledown_x \beta + x_k \bigtriangledown_x \gamma \]

其中，\(\alpha\)的计算，是三角形\(xx_jx_k\)的面积和三角形\(x_ix_jx_k\)的面积比，其中三角形\(xx_jx_k\)的面积的计算为\(xx_j\)向量在以\(x_jx_k\)为底的高的方向上的投影长度（即三角形的高），那么接着就可以通过(1/2底x高）计算三角形面积，具体如下：

\[\alpha = A_i / A_T \\ = \frac{\left( (x-x_j)\cdot \frac{(x_k - x_j)^\bot}{||x_k - x_j||_2} \right)||x_k-x_j||_2}{2A_T} \\ = (x-x_j)\cdot (x_k - x_j)^\bot / 2A_T \]

对x求导得：

\[\bigtriangledown_x \alpha = \frac{(x_k - x_j)^\bot}{2A_T} \]

同理可以求得：\(\bigtriangledown_x \beta, \bigtriangledown_x \gamma\)

其中，\((x_k - x_j)^\bot\)表示向量\(\vec{x_jx_k}\)逆时针旋转90度。

梯度公式如下：

\[\bigtriangledown_x x = \frac{(x_k - x_j)^\bot}{2A_T} + \frac{(x_j - x_i)^\bot}{2A_T} + \frac{(x_i - x_k)^\bot}{2A_T} \]

拉普拉斯算子

关于拉普拉斯比较通俗的解释见：https://zhuanlan.zhihu.com/p/67336297

拉普拉斯算子实际上衡量了空间中的每一个点处，该函数梯度倾向于增加还是减少。

连续曲面上的拉普拉斯算子具有以下性质：NULL；对称性；局部性；线性性；最大值原理；半正定性。

？？？怎么理解，离散拉普拉斯算子包含了集合处理的完整的谱信息？？？

顶点上的离散拉普拉斯算子的公式有：

\[(Lf)_i = \sum_{j\in \Omega(i)}\omega_{ij}(f_j - f_i) \]

满足以下性质：

• NULL：当f为常数的时候，结果为0；
• 对称性：\(\omega_{ij} = \omega_{ji}\), 暗示实对称矩阵，有实特征值和实特征向量；
• 局部性：ij不共边的时候\(\omega_{ij} = 0\) ；
• 线性性：\(\sum_{j}\omega_{ij}(f_i - f_j)=0\) ;
• 正权重：\(\omega_{ij} > 0, i\ne j\)

uniform Laplacian

当权重为1，或为\(1/N_i\)的时候，被称为uniform Laplacian。此时公式为：

\[(Lf)_i = \sum_{j\in \Omega(i)}(f_j - f_i) \ or \\ (Lf)_i = \frac{1}{N_i}\sum_{j\in \Omega(i)}(f_j - f_i) \]

Cotangent Laplacian

散度在面上的积分，可以转换成梯度在线上的积分，（TODO：CHECK）具体如下：

\[\int_{A_i}\Delta f dA = \int_{A_i} div\nabla f dA = \int_{\part A_i} (\nabla f) \cdot \vec{n} ds \]

结合图，可以更好的理解公式中的几个量的概念：

• \(A_i\)顶点i的邻域；
• \(\part A_i\)，邻域\(A_i\)的边界；
• \(\vec{n}\)，边界上向外的法向量；
• \(f\)，mesh上定义的信号；

针对一个三角形的情况，ac乘以它的out法向量加上cb乘上它的out法向量，就是向量ca逆时针旋转90度，加上向量bc逆时针旋转90度，等于向量ba逆时针旋转90度，即：

\[\int_{\part A_i\cap T} \nabla f \cdot \vec{n}ds = \nabla f\cdot (a-b)^\bot = \frac{1}{2}\nabla f \cdot (x_j - x_k)^\bot \]

对于每个三角形而言，xi的梯度都是常数，如下：

\[\nabla f = (f_j - f_i) \frac{(x_i - x_k)^\bot}{2A_T} + (f_k - f_i)\frac{(x_j-x_i)\bot}{2A_T} \]

因此代入后可得：

\[\int_{\part A_i\cap T} \nabla f \cdot \vec{n}ds = (f_j - f_i) \frac{(x_i - x_k)^\bot(x_j - x_k)^\bot}{4A_T} + (f_k - f_i)\frac{(x_j-x_i)^\bot (x_j - x_k)^\bot}{4A_T} \]

又因为：

\[A_T = \frac{1}{2}\sin \gamma_j ||x_j-x_i||||x_j-x_k|| \\ = \frac{1}{2}\sin \gamma_k ||x_i - x_k||||x_j - x_k|| \\ \cos \gamma_j = \frac{(x_j - x_i)\cdot (x_j - x_k)}{||x_j - x_i||||x_j - x_k||} \\ \cos \gamma_k = \frac{(x_i - x_k)\cdot (x_j - x_k)}{||x_i - x_k||||x_j - x_k||} \]

最后可得的：

\[\int_{A_i}\Delta f dA = \frac{1}{2}\sum_{j\in\Omega(i)}(\cot \alpha_{ij} + \cot \beta_{ij})(f_j - f_i) \]

右边项除以面积后，可以得到离散化的Laplace-Beltrami算子，如下：

\[\Delta f(v_i) = \frac{1}{2A_i}\sum_{j\in\Omega(i)}(\cot \alpha_{ij} + \cot \beta_{ij})(f_j - f_i) \]

离散曲率

Laplace-Beltrami算子可以用平均离散曲率表示，如下：

\[\Delta x = -2H\vec{n} \]