Atcoder beginner contest 394(ABCD,补E

atcoder beginner contest 394 (ABCD补E)

A：模拟

B：模拟

C：小模拟

idea:根据样例WWA，发现更新第一个WA为AC时，序列变为WAC，此时又出现一个WA，再次更新为ACC，所以每次找到WA时，往前更新W为AC即可

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 500;
struct node
{
	string s;
}a[N];
void solve()
{
	string s;
	cin>>s;
	int n = s.size();
	s = '%' + s;
	for(int i = 2;i <= n;i++)
	{
		if(s[i] == 'A' && s[i-1] == 'W')
		{
			s[i] = 'C';
			s[i-1] = 'A';
			int u = i-2;
			while(u >= 1 && s[u] == 'W' && u + 1 <=n)
			{
				s[u] = 'A';
				s[u+1] = 'C';
				u--;
			}
		}
	}
	for(int i = 1;i <= n;i++)	cout<<s[i];
	//cout<<s;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	int T = 1;
	//cin>>T;
	while(T--)
	{
		solve();
	}
}

D：栈模拟即可

#include<bits/stdc++.h>
#define N 1005
#define mod 998244353
using namespace std;
typedef long long ll;

void solve()
{
    stack<char>a;
    string s;
    cin>>s;
    a.push(s[0]);
    for(int i = 1; i < s.size();i++)
    {
        if(a.empty())   {a.push(s[i]);continue;}
        if(a.top()=='(' && s[i] == ')') a.pop();
        else if(a.top() == '[' && s[i] == ']')    a.pop();
        else if(a.top() == '<' && s[i] == '>')    a.pop();
        else a.push(s[i]);
    }
    if(a.empty())   cout<<"Yes\n";
    else    cout<<"No\n";
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T = 1;
    while(T--)
      solve();
    return 0;
}

E:

idea:正面考虑有点困难，得找到每两对点（i，j)之间的最短路，同时最短路序列还得是回文序列，根据回文序列的性质，现在假设两个点为i - > j 存在回文序列

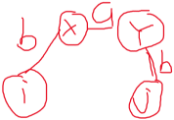
经过路径b-> a -> b 是点对(i，j)之间的最短回文路径，那么可以使用BFS(典）考虑，分别从i j,出发，从i -> X, j -> Y，再考虑X -> Y 之间是否存在路径（且回文），这样的正确性不用担心，一定是最短的（等下证， 只需要预处理好一步能到达的点，），现在把点的数量再增多一点，每对点对之间最长且存在路径为n对，这样队列点的数量是n^2 级别，枚举ij也为n^ 2,总的时间复杂度为n^ 4，对n = 100 可以通过。

idea:首先将(i,i)存入队列，本身为0，再将（i！=j) && aij !='-' （即一步能到达的点）存入队列，是否有点懂了，这样bfs每次从最短路逐步扩展，第一次从i->j 时，所得的一定是最短路，如果不存在，则ans(i,j)不会更新,而ans(i->x) ,ans(j->y)会更新。

#include<bits/stdc++.h>
#define N 105
#define mod 998244353
using namespace std;
typedef long long ll;

int ans[N][N];
char a[N][N];
//int q[N*N][2];
queue<pair<int,int>>q;
void solve()
{
    int n;
    cin>>n;
    memset(ans,-1,sizeof(ans));
    int hd = 1,tl = 1;
    for(int i = 1;i <= n;i++)
    {
        for(int j =1;j <= n;j++)
        {
            cin>>a[i][j];
        }
    }
    for(int i = 1;i <= n;i++)
    {
        ans[i][i] = 0;
        //q[tl][0] = i,q[tl][1] = i;
        //tl++;
        q.push({i,i});
    }
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= n;j++)
        {
            if(a[i][j] !='-' && i != j)
            {
                ans[i][j] = 1;
                //q[tl][0] = i,q[tl][1] = j;
                //tl++;
                q.push({i,j});
            }
        }
    }
    //while(hd < tl)
    while(!q.empty())
    {
        //int u = q[hd][0],v = q[hd][1];
        //hd++;
        auto [u,v] = q.front();
        q.pop();
        for(int i = 1;i <= n;i++)
        {
            if(a[i][u] !='-')
            {
                for(int j = 1;j <= n;j++)
                {
                    if(a[i][u] == a[v][j] && ans[i][j] == -1 && a[i][u]!='-')//注意这里的条件，因为是从i->u,j->v
                 
                    {
                        ans[i][j] = ans[u][v] + 2;//注意更新顺序是外面的路长
                        //q[tl][0] = i,q[tl][1] = j;
                        //tl++;
                        q.push({i,j});
                    }
                }
            }
        }
    }
    for(int i =1 ;i <= n;i++)
    {
        for(int j = 1;j <= n;j++)
        {
            cout<<ans[i][j]<<" ";
        }
        cout<<"\n";
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T = 1;
    while(T--)
      solve();
    return 0;
}