最短路问题
注:我们这里定义 \(mof=0x3f3f3f3f\),\(MOF=0x3f3f3f3f3f3f3f3f\),表示最短路径的无穷大,\(|V|\) 表示图中顶点数,\(|E|\) 表示图中边数。
\(Dijkstra\) 算法
1、原方法时间复杂度是 \(O(|V|^2)\) 的,是直接用 \(queue\) 来遍历每个点,没有任何优化,但是我们可以发现我们每次以最短路最短的那个点先执行遍历,就可以咋子某个时刻发现这个点不会更加优了,所以我们就可以对这个点进行标记了,可以发现选最小的那个点,相当于是利用了一个优先队列进行了 \(log|V|\) 的优化,所以这样时间复杂度就被我们降低至 \(O(|V|log|V|)\),空间复杂度 \(O(|V|)\)。
2、时间复杂度:\(O(|V|log|V|)\),空间复杂度:\(O(|V|)\)。
4、\(dijkstra\) 有个缺点,就是不能处理负权,而处理负权就需要用到我们的 \(spfa\) 算法了,后面会介绍。
5、单源最短路:\(O(|V|log|V|)\),多源最短路:\(O(|V|^2log|V|)\)。
template<typename T>
struct Dijkstra{
struct node{
int v;
T w;
node(int v = 0, T w = 0) : v(v), w(w) {}
};
struct S{
T id, dis;
bool operator< (const S &t) const {
return dis > t.dis;
}
};
int n;
vector<T> dist;
vector<bool> vis;
vector<vector<node>> g;
Dijkstra() {}
Dijkstra(int n_) : dist(n_ + 1, mof), vis(n_ + 1), g(n_ + 1) {
n = n_;
}
inline void init(int n_) {
n = n_;
dist.assign(n_ + 1, mof);
vis.assign(n_ + 1, 0);
g.assign(n_ + 1, node());
}
inline void add(int u, int v, const T &w) {
g[u].push_back({v, w});
}
inline void dijkstra(int beg) {
priority_queue<S> q;
dist[beg] = 0;
q.push({beg, 0});
while (!q.empty()) {
auto [u, disu] = q.top();
q.pop();
if (vis[u]) {
continue;
}
vis[u] = 1;
for (auto [v, w] : g[u]) {
if (w + dist[u] < dist[v]) {
dist[v] = w + dist[u];
q.push({v, dist[v]});
}
}
}
}
};
\(SPFA\) 算法
1、一种时间复杂度介于 \(|V|+|E|\) 到 \(|V||E|\) 的算法,优点在于可以处理负权,缺点就是容易被卡到 \(|V||E|\),如果是没有负权的情况下,我们可以直接选择 \(Dijkstra\) 算法。
2、该算法思想是维护一个队列,用一个 \(vis\) 数组标记目前处在队列中的元素,如果这个元素的最短路被缩短了,则更新最短路,并且如果这个元素不在队列中,我们就可以直接将这个点入队,最后队列为空结束,另外如果这个图里面有环的话,且这个环里面有负边权,就会导致队列中一直有元素,结束不了,所以如果对于有环图得特别判断下是否有环,除非题目告诉你无环。
4、有向图跑 \(spfa\),如图:
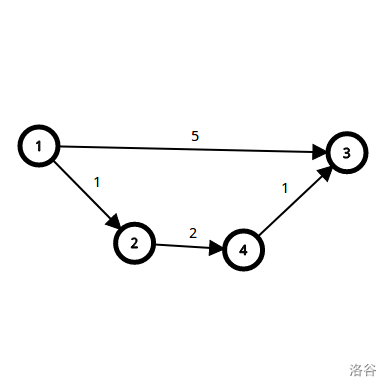
5、一般只用于求单源最短路,多源最短路会用到后面说的 \(Johnson\) 算法,时间复杂度更优。
template<typename T>
struct SPFA{
struct node{
int v;
T w;
node(int v = 0, T w = 0) : v(v), w(w) {}
};
int n;
vector<T> dist;
vector<bool> vis;
vector<vector<node>> g;
SPFA() {}
SPFA(int n_) : dist(n_ + 1, mof), vis(n_ + 1), g(n_ + 1) {
n = n_;
}
inline void init(int n_) {
n = n_;
dist.assign(n_ + 1, mof);
vis.assign(n_ + 1, false);
g.assign(n_ + 1, vector<node>());
}
inline void add(int u, int v, const T &w) {
g[u].push_back({v, w});
}
inline void spfa(int beg) {
queue<int> q;
dist[beg] = 0;
vis[beg] = true;
q.push(beg);
while (!q.empty()) {
int u = q.front();
q.pop();
vis[u] = false;// 出队
for (auto &[v, w] : g[u]) {
if (w + dist[u] < dist[v]) {
dist[v] = w + dist[u];// 更新最小值
if (!vis[v]) {
vis[v] = true;// 入队
q.push(v);
}
}
}
}
}
};
6、另外,\(spfa\) 还可以找是否存在负环:
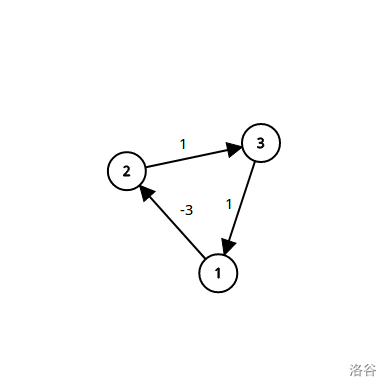
代码如下:
template<typename T>
struct SPFA{
struct node{
int v;
T w;
node(int v = 0, T w = 0) : v(v), w(w) {}
};
int n;
vector<T> dist;
vector<int> cnt;
vector<bool> vis;
vector<vector<node>> g;
SPFA() {}
SPFA(int n_) : dist(n_ + 1, mof), cnt(n_ + 1), vis(n_ + 1), g(n_ + 1) {
n = n_;
}
inline void init(int n_) {
n = n_;
dist.assign(n_ + 1, mof);
vis.assign(n_ + 1, false);
g.assign(n_ + 1, vector<node>());
}
inline void add(int u, int v, const T &w) {
g[u].push_back({v, w});
}
inline bool spfa(int beg) {// 返回false,表明有负环
queue<int> q;
dist[beg] = 0;
vis[beg] = true;
cnt[beg] = 1;
q.push(beg);
while (!q.empty()) {
int u = q.front();
q.pop();
vis[u] = false;// 出队
for (auto &[v, w] : g[u]) {
if (w + dist[u] < dist[v]) {
dist[v] = w + dist[u];// 更新最小值
if (!vis[v]) {
vis[v] = true;// 入队
cnt[v]++;
if (cnt[v] >= n) {
return false;
}
q.push(v);
}
}
}
}
return true;
}
};
\(Floyd\) 算法
1、时间复杂度:\(O(|V|^3)\),空间复杂度:\(O(|V|^2)\)。
2、利用的是动态规划思想处理的,都支持,只是时间复杂度高。
3、模版:洛谷B3647。
4、多源最短路:\(O(|V|^3)\)。
template<typename T>
struct Floyd{
int n;
vector<vector<T>> dist;
Floyd() {}
Floyd(int n_) : dist(n_ + 1, vector<T>(n_ + 1, mof)) {
n = n_;
for (int i = 0; i <= n_; i++) {
dist[i][i] = 0;
}
}
inline void init(int n_) {
n = n_;
dist.assign(n_ + 1, vector<T>(n_ + 1, mof));
for (int i = 0; i <= n_; i++) {
dist[i][i] = 0;
}
}
inline void add(int u, int v, const T &w) {
dist[u][v] = min(dist[u][v], w);
}
inline void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
};
\(Bellman-Ford\) 算法
1、可用于求一个单源图中是否有负环,与 \(dijkstra\) 相比有点在于可以求解负权的最短路,但时间复杂度比 \(dijkstra\) 差。
2、时间复杂度:\(O(|V||E|)\),空间复杂度:\(O(|V|)\)。
3、模版:洛谷P3385。
4、单源最短路:\(O(|V||E|)\)。
template<typename T>
struct Bellman_Ford{
struct node{
int u, v;
T w;
node(int u = 0, int v = 0, T w = 0) : u(u), v(v), w(w) {}
};
int n, tot;
vector<T> dist;
vector<node> g;
vector<int> pre;
Bellman_Ford() {}
Bellman_Ford(int n_) : dist(n_ + 1, mof), pre(n_ + 1) {
n = n_;
tot = 0;
}
inline void add(int u, int v, const T &w) {
tot++;
g.push_back({u, v, w});
}
inline void init(int n_) {
n = n_;
dist.assign(n_ + 1, mof);
pre.assign(n_ + 1, 0);
}
inline bool bellman_ford(int beg) {// 返回false表示有负权环,单源负环
dist.assign(n + 1, mof);
dist[beg] = 0;
bool f = true;
for (int i = 1; i <= n; i++) {
bool ok = true;
for (auto [u, v, w] : g) {
if (dist[u] == mof) {
continue;
}
if (dist[u] + w < dist[v]) {
dist[v] = dist[u] + w;
pre[v] = u;
ok = false;
if (i == n) {
f = false;
}
}
}
if (ok) {
break;
}
}
return f;
}
};
\(Johnson\) 算法
1、用于求带有负权的多源最短路,在求负权的多源最短路中他是最优的,主要利用的是 \(SPFA\) 算法和 \(Dijkstra\) 算法的结合,利用 \(spfa\) 算法使得图中的负权变为非负,从而可以通过 \(Dijkstra\) 算法来实现多源最短路。
2、时间复杂度:\(|V|^2log|V|+|V||E|\)。
3、模版:洛谷P5905。
4、注:如果一条边起点为 \(u\),终点为 \(v\),边权值为 \(w\),那么更新后的 \(w=w+h[u]-h[v]\),但是要记得将最后得到的 \(dist[beg][v]=dist[beg][v]+h[v]-h[u]\),这才是最条路径的最短路值,貌似这个算法不是特别重要。
template<typename T>
struct Johnson{
struct node{
int v;
T w;
};
struct S{
T id, dis;
bool operator< (const S &t) const {
return dis > t.dis;
}
};
int n;
vector<T> h;
vector<int> cnt;
vector<bool> vis;
vector<vector<T>> dist;
vector<vector<node>> g;
Johnson() {}
Johnson(int n_) : h(n_ + 1, MOF), cnt(n_ + 1), vis(n_ + 1), dist(n_ + 1, vector<T>(n_ + 1, MOF)), g(n_ + 1) {
n = n_;
}
inline void init(int n_) {
n = n_;
h.assign(n_ + 1, MOF);
cnt.assign(n_ + 1, 0);
vis.assign(n_ + 1, false);
g.assign(n_ + 1, vector<node>());
dist.assign(n_ + 1, vector<T>(n_ + 1, MOF));
}
inline void add(int u, int v, const T &w) {
g[u].push_back({v, w});
}
inline bool spfa() {
for (int i = 1; i <= n; i++) {// 虚拟源点,主要是为了将边权非负化。
add(0, i, 0);
}
h[0] = 0;
cnt[0]++;
vis[0] = true;
queue<int> q;
q.push(0);
while (!q.empty()) {
int u = q.front();
q.pop();
vis[u] = false;
for (auto [v, w] : g[u]) {
if (h[u] + w < h[v]) {
h[v] = h[u] + w;
if (!vis[v]) {
vis[v] = 1;
cnt[v]++;
q.push(v);
if (cnt[v] >= n) {
return false;
}
}
}
}
}
for (int i = 1; i <= n; i++) {
for (auto &[v, w] : g[i]) {
w += h[i] - h[v];
}
}
return true;
}
inline void dijkstra(int beg) {// 以beg为源点的最短路
vis.assign(n + 1, false);
dist[beg][beg] = 0;
priority_queue<S> q;
q.push({beg, 0});
while (!q.empty()) {
auto [u, w] = q.top();
q.pop();
if (vis[u]) {
continue;
}
vis[u] = true;
for (auto [v, w] : g[u]) {
if (dist[beg][u] + w < dist[beg][v]) {
dist[beg][v] = dist[beg][u] + w;
q.push({v, dist[beg][v]});
}
}
}
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号