主席树
动态开点线段树
1、与普通线段树相比,优点在于对于 \(1e8-1e18\) 以内的权值维护不需要进行离散化,可直接进行动态开点维护,更加方便,但是这样会比原来线段树维护的空间复杂度来得高,空间复杂度更差一些。
2、如图说明动态开点过程:
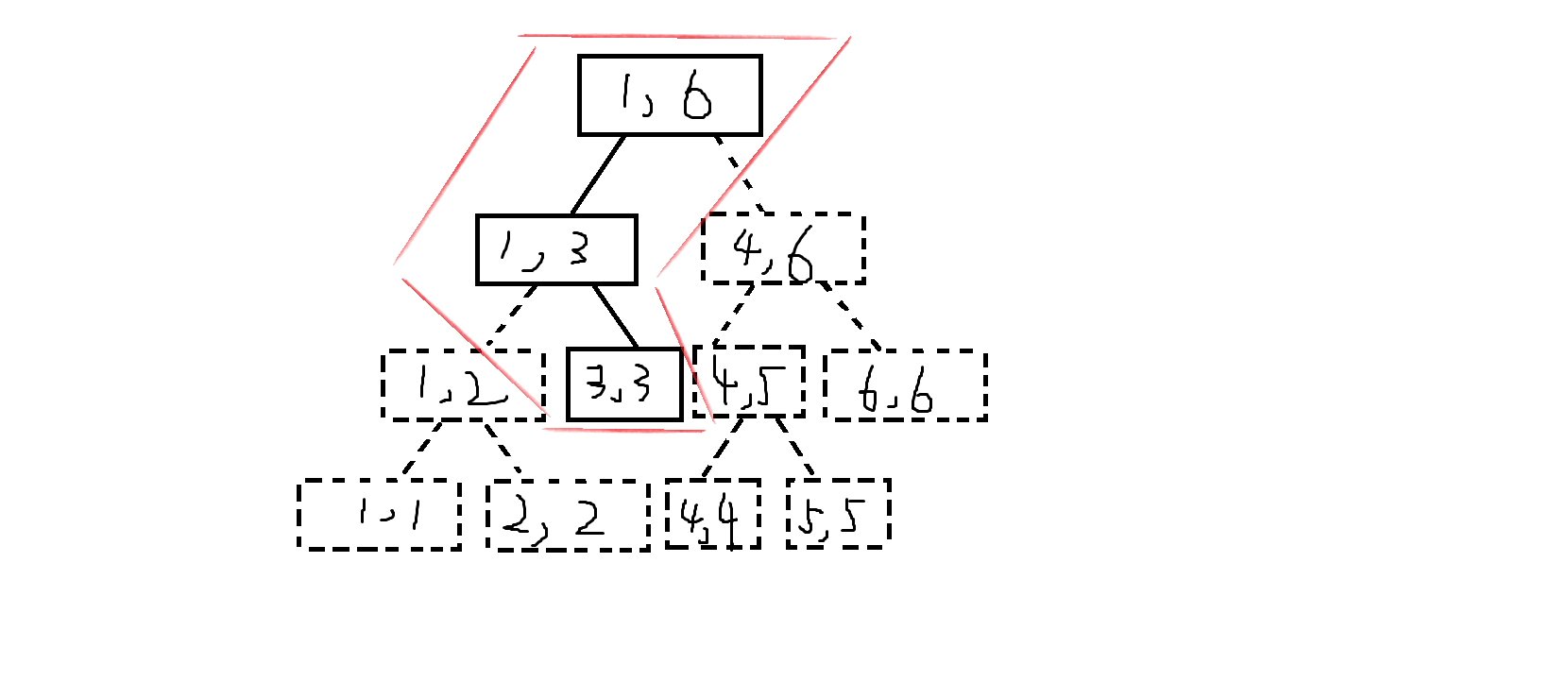
可以发现我们不需要用到区间 \([6,6]\) 的两个子节点,所以这部分相当于动态开点过程中所省略的点(所省略的空间)。
3、动态开点线段树常用于在线操作,因为我们知道对值域离散化,我们也是可以用普通线段树维护的,但是这种需要离线操作,那如果题目强制要求在线操作,那就得使用动态开店线段树了,时间复杂度为 \(O(nlogn)\),空间复杂度为 \((n + q)log(MAX(val))\)(开这么多点就差不多了)。
template<typename T>
struct R_tree{
struct node{
T l, r, siz, sum;
node(T l = 0, T r = 0, T siz = 0, T sum = 0) : l(l), r(r), siz(siz), sum(sum) {
}
#define rt(x) tree[x]
#define ls(x) tree[x].l
#define rs(x) tree[x].r
};
int n, m, tot;
vector<node> tree;
R_tree() {}
R_tree(int n_, int m_, int MAX = 15) : tree((n_ + m_) * MAX + 1) {
n = n_;
m = m_;
tot = 1;
}
inline void init(int n_) {
n = n_;
tot = 1;
tree.assign(n_ << 5, node());
}
inline node hb(int l, int r) {
node k;
k.l = l;
k.r = r;
k.siz = rt(l).siz + rt(r).siz;
k.sum = rt(l).sum + rt(r).sum;
return k;
}
inline node hb(node i, node j) {
node k;
k.siz = i.siz + j.siz;
k.sum = i.sum + j.sum;
return k;
}
inline void push_up(T x) {
rt(x) = hb(ls(x), rs(x));
}
inline void push_mark(T x, T l, T r) {
T mid = l + r >> 1;
if (!ls(x)) {
ls(x) = ++tot;
rt(tot) = node(0, 0, mid - l + 1, 0);
}
if (!rs(x)) {
rs(x) = ++tot;
rt(tot) = node(0, 0, r - mid, 0);
}
}
inline void update(T root, T l, T r, T ql, T qr, const T &opt) {
T mid = l + r >> 1;
if (r < ql || l > qr) {
return;
}
if (l >= ql && r <= qr) {
rt(root).sum += opt;
return;
}
push_mark(root, l, r);
update(ls(root), l, mid, ql, qr, opt);
update(rs(root), mid + 1, r, ql, qr, opt);
push_up(root);
}
inline node query(T root, T l, T r, T ql, T qr) {
T mid = l + r >> 1;
if (r < ql || l > qr) {
return node();
}
if (l >= ql && r <= qr) {
return rt(root);
}
push_mark(root, l, r);
return hb(query(ls(root), l, mid, ql, qr), query(rs(root), mid + 1, r, ql, qr));
}
};
可持久化数组:求解每次修改后的版本下每个位置的权值
1、模版:LUOGU,利用的也是动态开点的思路,因为每修改一次都只会增加 \(logn\) 个点,所以我们可以对每次修改后的数组进行一个版本更替,因为每次修改的点就那一个,所以可以直接重复利用之前的点即可省掉大部分空间。
2、时间复杂度:\(O(nlogn)\),空间复杂度:\(O((n + m)log(MAX))\)。
template<typename T>
struct HJT_tree{
struct node{
T l, r, sum;
node(T l = 0, T r = 0, T sum = 0) : l(l), r(r), sum(sum) {}
#define rt(x) tree[x]
#define ls(x) tree[x].l
#define rs(x) tree[x].r
};
int n, m, tot;
vector<T> a, r_t;
vector<node> tree;
HJT_tree() {}
HJT_tree(int n_, int m_, int MAX = 15) : a(n_ + 1), r_t(m_ + 1), tree((n_ + m_) * MAX + 1) {
n = n_;
m = m_;
tot = 0;
}
inline void init() {
}
inline void build(int &root, int l, int r) {
root = ++tot;
int mid = l + r >> 1;
if (l == r) {
rt(root).sum = a[l];
return;
}
build(ls(root), l, mid);
build(rs(root), mid + 1, r);
}
inline void update(int &now, int before, int l, int r, int pos, const T &v) {
int mid = l + r >> 1;
now = ++tot;
rt(now) = rt(before);
if (l == r) {
rt(now).sum = v;
return;
}
if (pos <= mid) {
update(ls(now), ls(before), l, mid, pos, v);
} else {
update(rs(now), rs(before), mid + 1, r, pos, v);
}
}
inline T query(int root, int l, int r, int pos) {
int mid = l + r >> 1;
if (l == r) {
return rt(root).sum;
}
if (pos <= mid) {
return query(ls(root), l, mid, pos);
} else {
return query(rs(root), mid + 1, r, pos);
}
}
};
可持久化线段树:静态区间第 \(k\) 小
1、这个也是比较经典的题目,和上面的可持久化线段树一是一样的思路,都是动态开点,每次维护新的 \(logn\) 个点,然后里面线段树里面维护的是每个数的前缀数目,所以就可以用 \(rt[r]\) 版本减去 \(rt[l - 1]\) 版本的值就可以得到所有值在区间 \([l,r]\) 内的数目,这部分就可以进行树上二分操作来求得我们所需要找的第 \(k\) 小数。
2、时间复杂度:\(O(nlogn)\),空间复杂度:\(O((n + m)log(MAX))\),模版:LUOGU。
3、另外,我在另外一篇博客还介绍了另一种求解区间第 \(k\) 小的算法,也是和它一样只能处理静态区间第 \(k\) 小的问题,博客地址:划分树。
template<typename T>
struct HJT_tree{
struct node{
T l, r, sum;
node(T l = 0, T r = 0, T sum = 0) : l(l), r(r), sum(sum) {}
#define rt(x) tree[x]
#define ls(x) tree[x].l
#define rs(x) tree[x].r
};
int n, tot;
vector<T> r_t;
vector<node> tree;
HJT_tree() {}
HJT_tree(int n_, int MAX = 15) : r_t(n_ + 1), tree(n_ * MAX + 1) {
n = n_;
tot = 0;
}
inline void init() {
}
inline void update(int &now, int before, int l, int r, int pos, const T &v) {
int mid = l + r >> 1;
now = ++tot;
rt(now) = rt(before);
rt(now).sum += v;
if (l == r) {
return;
}
if (pos <= mid) {
update(ls(now), ls(before), l, mid, pos, v);
} else {
update(rs(now), rs(before), mid + 1, r, pos, v);
}
}
inline T query(int now, int before, int l, int r, int k) {
int mid = l + r >> 1;
if (l == r) {
return l;
}
T sum = rt(ls(now)).sum - rt(ls(before)).sum;
if (sum >= k) {
return query(ls(now), ls(before), l, mid, k);
} else {
return query(rs(now), rs(before), mid + 1, r, k - sum);
}
}
};
区间 \(MEX\)
1、利用主席树的思想我们只需要像求静态区间第 \(k\) 小那样,只需要维护下每个数在新版本下的最新位置(每个版本只会有一个值的位置才会变化,所以时间复杂度是 \(logn\) 级别的),然后再更新下区间的 \(min\),最后就可以直接查询在 \(r_t[r]\) 版本下最后一次位置小于 \(l\) 的最小权值。
2、方法一:就是现在讲的主席树,并且这种方法为在线算法;方法二:离线 + 线段树,为离线算法,和主席树是一样的思想,不过需要离线处理罢了,这里我就不详细解释了,之后我会在这篇博客更新这种写法。
3、方法一:时间复杂度:\(O(nlogn)\),空间复杂度:\(O(nlogn)\)。
4、模版:洛谷P4137。
template<typename T>
struct Mex_tree{
struct node{
int l, r;
T mn;
node(int l = 0, int r = 0, T mn = 0) : l(l), r(r), mn(mn) {}
#define rt(x) tree[x]
#define ls(x) tree[x].l
#define rs(x) tree[x].r
};
int n, tot;
vector<int> r_t;
vector<node> tree;
Mex_tree() {}
Mex_tree(int n_, int MAX = 25) : r_t(n_ + 1), tree(n_ * MAX + 1) {
n = n_;
tot = 0;
}
inline void push_up(int root) {
rt(root).mn = min(rt(ls(root)).mn, rt(rs(root)).mn);
}
inline void ins(int &now, int before, int l, int r, int pos, const T &v) {
int mid = l + r >> 1;
now = ++tot;
rt(now) = rt(before);
if (l == r) {
rt(now).mn = v;
return;
}
if (pos <= mid) {
ins(ls(now), ls(before), l, mid, pos, v);
} else {
ins(rs(now), rs(before), mid + 1, r, pos, v);
}
push_up(now);
}
inline int query(int now, int l, int r, int pos) {
int mid = l + r >> 1;
if (l == r) {
return l;
}
if (rt(ls(now)).mn < pos) {
return query(ls(now), l, mid, pos);
} else {
return query(rs(now), mid + 1, r, pos);
}
}
};
void solve() {
int n, m;
read(n, m);
vector<int> a(n + 2);
Mex_tree<int> tr(n + 1);
for (int i = 1; i <= n; i++) {
read(a[i]);
tr.ins(tr.r_t[i], tr.r_t[i - 1], 0, n + 1, min(n + 1, a[i]), i);
}
for (int i = 1; i <= m; i++) {
int l, r;
read(l, r);
printf("%d\n", tr.query(tr.r_t[r], 0, n + 1, l));
}
}
主席树维护区间种类数
1、方法一:主席树在线维护;方法二:树状数组离线维护。
2、时间复杂度:\(O(nlogn)\),空间复杂度:\(O(nlog(MAX))\)。
3、模版:洛谷1972。
template<typename T>
struct Persistent{
struct node{
int l, r;
T sum;
node(int l = 0, int r = 0, T sum = 0) : l(l), r(r), sum(sum) {}
#define rt(x) tree[x]
#define ls(x) tree[x].l
#define rs(x) tree[x].r
};
int n, tot;
vector<int> r_t;
vector<node> tree;
Persistent() {}
Persistent(int n_, int MAX = 20) : r_t(n_ + 1), tree(n_ * MAX + 1) {
n = n_;
tot = 0;
}
inline void init() {
}
inline void update(int &now, int before, int l, int r, int pos, const T &v) {
int mid = l + r >> 1;
now = ++tot;
rt(now) = rt(before);
rt(now).sum += v;
if (l == r) {
return;
}
if (pos <= mid) {
update(ls(now), ls(before), l, mid, pos, v);
} else {
update(rs(now), rs(before), mid + 1, r, pos, v);
}
}
inline T query(int now, int before, int l, int r, int pos) {
int mid = l + r >> 1;
if (l == r) {
return rt(now).sum - rt(before).sum;
}
if (pos <= mid) {
return query(ls(now), ls(before), l, mid, pos) + rt(rs(now)).sum - rt(rs(before)).sum;
} else {
return query(rs(now), rs(before), mid + 1, r, pos);
}
}
};
void solve() {
int n;
cin >> n;
vector<int> a(n + 1);
vector<int> nxt(n + 1, n + 1);
vector<int> idx(1000001);
for (int i = 1; i <= n; i++) {
cin >> a[i];
nxt[idx[a[i]]] = i;
idx[a[i]] = i;
}
Persistent<int> tr(n, 30);
for (int i = 1; i <= n; i++) {
tr.update(tr.r_t[i], tr.r_t[i - 1], 1, 1000000, nxt[i], 1);
}
int m;
cin >> m;
for (int i = 1, l, r; i <= m; i++) {
cin >> l >> r;
cout << tr.query(tr.r_t[r], tr.r_t[l - 1], 1, 1000000, r + 1) << '\n';
}
}
注:依我做题而言,如果你用的是动态数组 \(vector\),那部分 \(tree\) 数组的那部分 \(log(MAX)\) 尽量开大点,尽量多加个二或以上,如(log(MAX) + 2),毕竟保险为见。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号