笛卡尔树

笛卡尔树：

1、性质：

• 具有键值 \((k, w)\)，且 \(k\) 为下标，\(w\) 满足小根堆性质。
• 具有小根堆性质，任意一个节点的子树节点数值都比其来得大，每个节点与其子树中的所有节点连起来是一段连续区间。

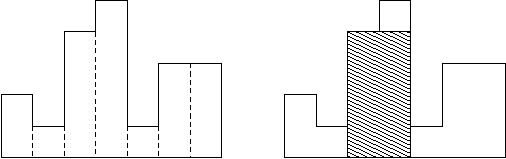
2、用途：可以用它来计算一个数组中子矩阵的最大值。

3、如图：

template<typename T>
struct Dker_tree{
    T ans;
	int n, top, root;
	vector<T> ls, rs, st, a, siz;
	
    Dker_tree() {}
	Dker_tree(int n_) : ls(n_ + 1), rs(n_ + 1), st(n_ + 1), a(n_ + 1), siz(n_ + 1) {
		n = n_;
        root = 1;
        top = 0;
        ans = T{};
        init();
	}
	
	inline void init() {
		top = 0;
		for (int i = 1; i <= n; i++) {
			cin >> a[i];
			int k = top;
			while (k > 0 && a[st[k]] > a[i]) k--;
			if (k) rs[st[k]] = i;
			else root = i;
			if (k < top) {
				ls[i] = st[k + 1];
			}
			st[++k] = i;
			top = k;
		}
	}
	
	inline void dfs1(int root) {
		/*利用中序遍历输出键值, 可用来验证此树是不是笛卡尔树*/
		if (!root) {
			return;
		}
		
		dfs1(ls[root]);
		cout << a[root] << ' ';
		dfs1(rs[root]);
	}
	
	inline T dfs2(int now) {
		if (!now) {
			return T{};
		}
		
		T sz = dfs2(ls[now]);
		sz += dfs2(rs[now]);
		siz[now] = sz + 1;
		ans = max(ans, siz[now] * a[now]);
		return siz[now];
	}
};

void solve() {
	int n;
	cin >> n;
	Dker_tree<i64> t(n);
	t.dfs1(t.root);
}