树状数组和二维树状数组
注:树状数组中 \(lowbit\) 函数代表的是这个数所维护的区间长度。
树状数组(单点查询、区间修改)
1、时间复杂度为 add:\(O(log\ n)\),query:\(O(log\ n)\)。
2、模版:洛谷P3368。
template<typename T>
struct Fenwick{
int n;
vector<T> a;
Fenwick() {}
Fenwick(int n_) {
init(n_);
}
inline void init(int n_) {
n = n_;
a.assign(n + 1, T{});
}
inline int low_bit(int x) {
return x & -x;
}
inline void add(int x, const T &v) {
for (int i = x; i <= n; i += low_bit(i)) {
a[i] += v;
}
}
inline void rangeAdd(int l, int r, const T &v) {
add(l, v);
add(r + 1, -v);
}
inline T query(int x) {
T sum{};
for (int i = x; i >= 1; i -= low_bit(i)) {
sum += a[i];
}
return sum;
}
};
树状数组(区间查询,单点修改)
1、时间复杂度:add \(O(log\ n)\),query \(O(log\ n)\)。
2、模版:洛谷P3374。
template<typename T>
struct Fenwick{
int n;
vector<T> a;
Fenwick() {}
Fenwick(int n_) : a(n_ + 1) {
n = n_;
}
inline int low_bit(int x) {
return x & -x;
}
inline void add(int x, const T &v) {
for (int i = x; i <= n; i += low_bit(i)) {
a[i] += v;
}
}
inline T query(int x) {
T sum{};
for (int i = x; i >= 1; i -= low_bit(i)) {
sum += a[i];
}
return sum;
}
inline T rangeQuery(int L, int R) {
return query(R) - query(L - 1);
}
inline int select(const T &k) {
int x = 0;
T cnt{};
for (int i = 1 << __lg(n); i; i >>= 1) {
if (x + i <= n && cnt + a[i + x] <= k) {
x += i;
cnt += a[x];
}
}
return x;
}
};
树状数组(区间查询,区间修改)
1、时间复杂度为同上(常数多了一倍,因为用了两个树状数组存储两个不同的值)。
2、假设我们对区间 \([l,r]\) 的每个元素都加上 \(x\),然后我们记录数组的前缀和为数组 \(c\),那么就有:
- 对于 \(1\le i\lt l\) 的 \(c'[i] = c[i]\),
- 对于 \(l\le i\le r\) 的 \(c'[i] = c[i] + (i - l + 1)\times x\),
- 对于 \(i\gt r\) 的 \(c'[i] = c[i] + (r - l + 1)\times x\),
3、那么其实对于第二种情况相当于可以拆成 \(c'[i] = c[i] - (l - 1)\times x + i\times x\)。
现在就可以套两个树状数组一分别处理 \(Bit1: - (l - 1)\times x、r\times x\),和 \(Bit2: x、-x\),我们维护的是数组前缀和,所以某段区间的值就是两个树状数组的前缀和 \(r\) 减去前缀和 \(l - 1\) 的总和。
4、模版:loj。
template<typename T>
struct Fenwick{
int n;
vector<T> a;
Fenwick() {}
Fenwick(int n_) {
init(n_);
}
inline void init(int n_) {
n = n_;
a.assign(n + 1, T{});
}
inline int low_bit(int x) { return x & -x; }
inline void add(int x, const T &v) {
for (int i = x; i <= n; i += low_bit(i)) {
a[i] += v;
}
}
inline void rangeAdd(int l, int r, const T &v) {
add(l, v);
add(r + 1, -v);
}
inline T query(int x) {
T sum{};
for (int i = x; i >= 1; i -= low_bit(i)) {
sum += a[i];
}
return sum;
}
};
template<typename T>
struct Fenwick_{
int n;
Fenwick<T> bit1, bit2;
Fenwick_(int n_) : bit1(n_), bit2(n_) {
n = n_;
}
inline void rangeAdd(T l, T r, const T &v) {
bit1.add(l, -(l - 1) * v);
bit1.add(r + 1, r * v);
bit2.add(l, v);
bit2.add(r + 1, -v);
}
inline T query(T x) {// 求的是前缀前缀和(1-x)
T sum{};
sum += bit1.query(x) + bit2.query(x) * x;
return sum;
}
inline T RangeQuery(T l, T r) {
return query(r) - query(l - 1);
}
};
void solve() {
int n, m;
cin >> n >> m;
vector<i64> a(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
Fenwick_<i64> ans(n);
for (i64 i = 1; i <= n; i++) {
ans.rangeAdd(i, i, a[i]);
}
for (int i = 1; i <= m; i++) {
int opt;
cin >> opt;
if (opt == 1) {
i64 l, r, x;
cin >> l >> r >> x;
ans.rangeAdd(l, r, x);
} else {
i64 x, y;
cin >> x >> y;
i64 sum = ans.RangeQuery(x, y);
cout << sum << '\n';
}
}
}
树状数组维护区间 \(max\)(单点修改,区间查询)
1、时间复杂度为 \(O(log^{2}n)\)
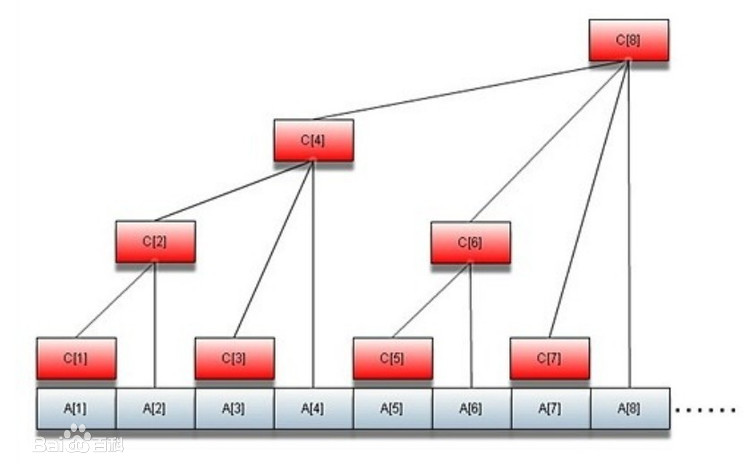
2、首先我们可以发现每次单点修改只会对数组中 \(x,x+low_bit(x)...\) 索引的值产生影响,而我们又不能直接对这些值赋值为 \(v\),但是我们可以发现这些值又只会由大约 \(log\ n\) 个数的 \(max\) 组成,且是有规律的,如 \(c[8] = max({v, c[4], c[6], c[7]})\),所以总时间复杂度为 \(log^{2}n\),如图,可以更加明确的看出来:
template<typename T>
struct Fenwick_Max{
int n;
vector<T> num, a;
/*num指的是原数组修改完后的值,a为树状数组维护的区间max*/
Fenwick_Max() {}
Fenwick_Max(int n_) : num(n_ + 1), a(n_ + 1) {
n = n_;
}
inline void init(int n_) {
n = n_;
num.assign(n_ + 1, 0);
a.assign(n_ + 1, 0);
}
inline int low_bit(int x) {
return x & -x;
}
inline void add(int x, const T &v) {
num[x] = v;
while (x <= n) {
a[x] = v;
for (int i = 1; i < low_bit(x); i += low_bit(i)) {
a[x] = max(a[x], a[x - i]);
}
x += low_bit(x);
}
}
inline T RangeQuery(int l, int r) {
T mx{};
while (l <= r) {
mx = max(mx, num[r]);
r--;
for (; r - l >= low_bit(r); r -= low_bit(r)) {
mx = max(mx, a[r]);
}
}
return mx;
}
};
二维树状数组(单点修改、区间查询)
1、时间复杂度为 \(log\ nlog\ m\)。
2、模版:loj。
template<typename T>
struct Fenwick{
int n;
vector<T> a;
Fenwick() {}
Fenwick(int n_) {
init(n_);
}
inline void init(int n_) {
n = n_;
a.assign(n_ + 1, T{});
}
inline int low_bit(int x) { return x & -x; }
inline void add(int x, const T &v) {
for (int i = x; i <= n; i += low_bit(i)) {
a[i] += v;
}
}
inline void rangeAdd(int l, int r, const T &v) {
add(l, v);
add(r + 1, -v);
}
inline T query(int x) {
T sum{};
for (int i = x; i >= 1; i -= low_bit(i)) {
sum += a[i];
}
return sum;
}
};
template<typename T>
struct Fenwick__{
int n, m;
vector<Fenwick<T>> bit;
Fenwick__() {}
Fenwick__(int n_, int m_) : bit(n_ + 1, Fenwick<T>(m_ + 1)) {
n = n_;
m = m_;
}
inline int low_bit(int x) { return x & -x; }
inline void init(int n_, int m_) {
n = n_;
m = m_;
bit.assign(n_ + 1, Fenwick<T>(m_ + 1));
}
inline void add(int x, int y, const T &v) {
for (int i = x; i <= n; i += low_bit(i)) {
bit[i].add(y, v);
}
}
inline T query(int x, int y) {
T sum{};
for (int i = x; i >= 1; i -= low_bit(i)) {
sum += bit[i].query(y);
}
return sum;
}
inline T rangeQuery(int a, int b, int c, int d) {
return query(c, d) - query(c, b - 1) - query(a - 1, d) + query(a - 1, b - 1);
}
};
二维树状数组(区间修改、区间查询)。
1、模版:洛谷P4514。
???


 浙公网安备 33010602011771号
浙公网安备 33010602011771号