完全背包问题详解

引言

背包问题是动态规划（DP）的一类问题。

背包问题的核心其实就是组合问题，在一个背包中有若干物品，在某种限制条件下，选出最好的组合。

完全背包问题

特点：每件物品有无限个。

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。
第 i 种物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
10

y氏DP分析法：参考自AcWing闫学灿。

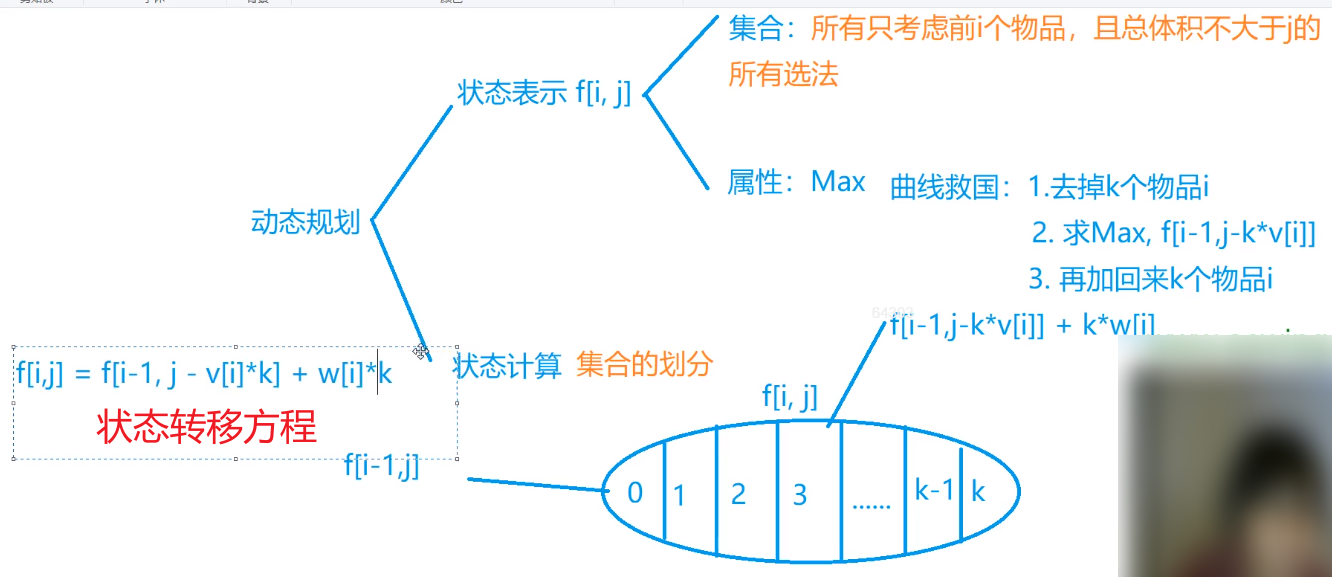
三重循环（朴素）做法：数据加强后TLE，重在理解写法。

// y总题解
// 注意:TLE
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n,m;
int dp[N][N];
int v[N],w[N];
int main(){
    cin >> n >> m;

    for (int i = 1;i <= n;i++) cin >> v[i] >> w[i];

    // i从1开始枚举，j从0开始枚举
    for (int i = 1;i <= n;i++)
        for (int j = 0;j <= m;j++)
            for (int k = 0;k*v[i]<=j;k++)
                dp[i][j] = max(dp[i][j],dp[i-1][j-k*v[i]] + k*w[i]);
    cout << dp[n][m] << endl;
    return 0;
}

---

优化：

时间复杂度：O(n*m)。

减少一重循环。

对比01背包问题的状态转移方程是：f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i])

我们很容易发现，01背包和完全背包的区别就在于第二项的第一维，前者是i-1，而后者是i。

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n,m;
int dp[N][N];
int v[N],w[N];
int main(){
    cin >> n >> m;

    for (int i = 1;i <= n;i++) cin >> v[i] >> w[i];

    for (int i = 1;i <= n;i++)
        for (int j = 0;j <= m;j++){
            dp[i][j] = dp[i-1][j];// 特判第一种情况
            if (j >= v[i]) dp[i][j] = max(dp[i][j],dp[i][j-v[i]]+w[i]);
        }
        
    cout << dp[n][m] << endl;
    return 0;
}

因为和01背包代码很相像，我们很容易想到进一步优化。

这里先介绍降低第一维度的题解，在01背包中没有提到过。

就是将第一个维度直接&1，那么数据就会保存在dp[0][x]和dp[1][x]中。只要用到dp[2][N]这么大的数组就足够了。（这就是一个两层的滚动数组）

我们还可以再优化，边读入边处理。

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n,m;
int dp[2][N];
int v,w;
int main(){
    cin >> n >> m;

    for (int i = 1;i <= n;i++){
        cin >> v >> w;
        for (int j = 0;j <= m;j++){
            dp[i&1][j] = dp[(i-1)&1][j];
            if (j >= v) dp[i&1][j] = max(dp[i&1][j],dp[i&1][j-v] + w);
        }
    }    
    cout << dp[n&1][m] << endl;
    return 0;
}

接下来是类似01背包的更优化的滚动数组。

利用滚动数组优化成一维：

由于完全背包用到的dp[i][j-v[i]]是第i（即本次）次的结果，不像01背包一样用到的是上一次的结果，所以可以直接正向枚举。

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n,m;
int dp[N];
int v[N],w[N];
int main(){
    cin >> n >> m;

    for (int i = 1;i <= n;i++) cin >> v[i] >> w[i];

    for (int i = 1;i <= n;i++)
        for (int j = v[i];j <= m;j++){
            dp[j] = max(dp[j],dp[j-v[i]]+w[i]);
        }
        
    cout << dp[m] << endl;
    return 0;
}