[LeetCode] 319. Bulb Switcher 灯泡开关
There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.
Return the number of bulbs that are on after n rounds.
Example 1:
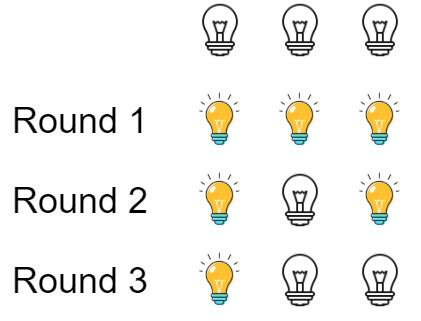
Input: n = 3 Output: 1 Explanation: At first, the three bulbs are [off, off, off]. After the first round, the three bulbs are [on, on, on]. After the second round, the three bulbs are [on, off, on]. After the third round, the three bulbs are [on, off, off]. So you should return 1 because there is only one bulb is on.
Example 2:
Input: n = 0 Output: 0
Example 3:
Input: n = 1 Output: 1
Constraints:
0 <= n <= 109
这道题给了n个灯泡,第一次打开所有的灯泡,第二次每两个更改灯泡的状态,第三次每三个更改灯泡的状态,以此类推,第n次每n个更改灯泡的状态。让我们求n次后,所有亮的灯泡的个数。此题是CareerCup 6.6 Toggle Lockers 切换锁的状态。
那么先枚举个小例子来分析下,比如只有5个灯泡的情况,'X'表示灭,‘√’表示亮,如下所示:
初始状态: X X X X X
第一次: √ √ √ √ √
第二次: √ X √ X √
第三次: √ X X X √
第四次: √ X X √ √
第五次: √ X X √ X
那么最后发现五次遍历后,只有1号和4号灯泡是亮的,而且很巧的是它们都是平方数,是巧合吗,还是其中有什么玄机。仔细想想,对于第n个灯泡,只有当次数是n的因子的之后,才能改变灯泡的状态,即n能被当前次数整除,比如当n为 36 时,它的因数有 (1,36), (2,18), (3,12), (4,9), (6,6), 可以看到前四个括号里成对出现的因数各不相同,括号中前面的数改变了灯泡状态,后面的数又变回去了,等于灯泡的状态没有发生变化,只有最后那个 (6,6),在次数6的时候改变了一次状态,没有对应其它的状态能将其变回去了,所以灯泡就一直是点亮状态的。所以所有平方数都有这么一个相等的因数对,即所有平方数的灯泡都将会是点亮的状态。
那么问题就简化为了求1到n之间完全平方数的个数,可以用 force brute 来比较从1开始的完全平方数和n的大小,参见代码如下:
解法一:
class Solution { public: int bulbSwitch(int n) { int res = 1; while (res * res <= n) ++res; return res - 1; } };
还有一种方法更简单,我们直接对n开方,在 C++ 里的 sqrt 函数的返回值若用 int 变量来接的话可以自动转为一个整型数,这个整型数的平方最接近于n,即为n包含的所有完全平方数的个数,参见代码如下:
解法二:
class Solution { public: int bulbSwitch(int n) { return sqrt(n); } };
讨论:这道题有个 follow up 就是,如果 toggle 的顺序不是 1,2,3,4...,而是 1,3,5,7...,或者是 2,4,6,8... 的话,还怎么做?博主没有想出像解法二那样简便的方法,只是大概想了想,如果各位大神有更好的方法,请一定要在下方留言啊。博主想的是,比如对于 1,3,5,7...,那么就是先把所有的灯点亮,然后关掉 3,6,9,12,15... 等的灯,然后 toggle 的是 5,10,15... 等等,然后再 toggle 的是 7,14,21...,可以发现,纯2的倍数的灯永远不会被改变,比如 2,4,8,16... 这些灯状态不会变,有些灯只会变一次,比如 3,6,9 等,而有些灯会变两次,比如15(3x5),21(3x7),35(5x7)等,有些灯会变三次,比如 105(3x5x7),那么可以观察出规律了,toggle 的次数跟奇数因子的数字有关(注意这里的奇数因子不包括1),只要有奇数个奇因子,那么灯就是灭的,只要有偶数个奇因子,那么灯就是亮的。
Github 同步地址:
https://github.com/grandyang/leetcode/issues/319
类似题目:
Minimum Number of K Consecutive Bit Flips
Bulb Switcher III
参考资料:
https://leetcode.com/problems/bulb-switcher/
https://leetcode.com/problems/bulb-switcher/discuss/77104/Math-solution..
https://leetcode.com/problems/bulb-switcher/discuss/77112/Share-my-o(1)-solution-with-explanation






