golang实现迪杰斯特拉(Dijkstra)算法

思路

Dijkstra算法的基本思想是贪心策略，即每次选择当前未访问的顶点中距离源点最近的顶点（我们假设该点为X点），这样就保证获得了源点（就是需要求解的点）到X点最近的路径，并将其标记为已访问，然后更新该顶点邻接顶点的距离估计值。算法通过不断迭代，逐步扩展到图中所有顶点，直到所有顶点都被访问为止‌

代码的大概步骤描述如下：

1、创建一个列表visit，其下标代表点的编号，用于记录已经找到最短路径的顶点，也就是已经遍历过的点。

2、创建一个列表dis，其下标代表点的编号，其值代表源点到 其下标对应的点的最短路径距离 （或 路径，这个看业务需求去存储），源点所对应的编号值为0，最开始的时候所有点（除了源点）都是无穷大

3、从源点开始发散，找其指向的下游点，记录这些未被访问的下游点中距离最近的点X（或者说权值最小的点，无所谓的这个说法，会随着业务不同变化，意会即可），其实就是dis中最小的

4、然后将visit中对应的X点，标记为已被遍历，然后更新所有X点的所指向的下游点在dis中的值，比如其中一个X的下游点是Y，那么就是dis[Y] = dis[X] + XY，其实就是源点到X的距离，加上XY之间的距离

5、重复3、4，直到所有点被遍历一次

图解

上面这么干说可能不太好想象，不太好理解，看图就会好一些

随便画一个图，我们选择A点为源点，求解A到所有点的最短路径

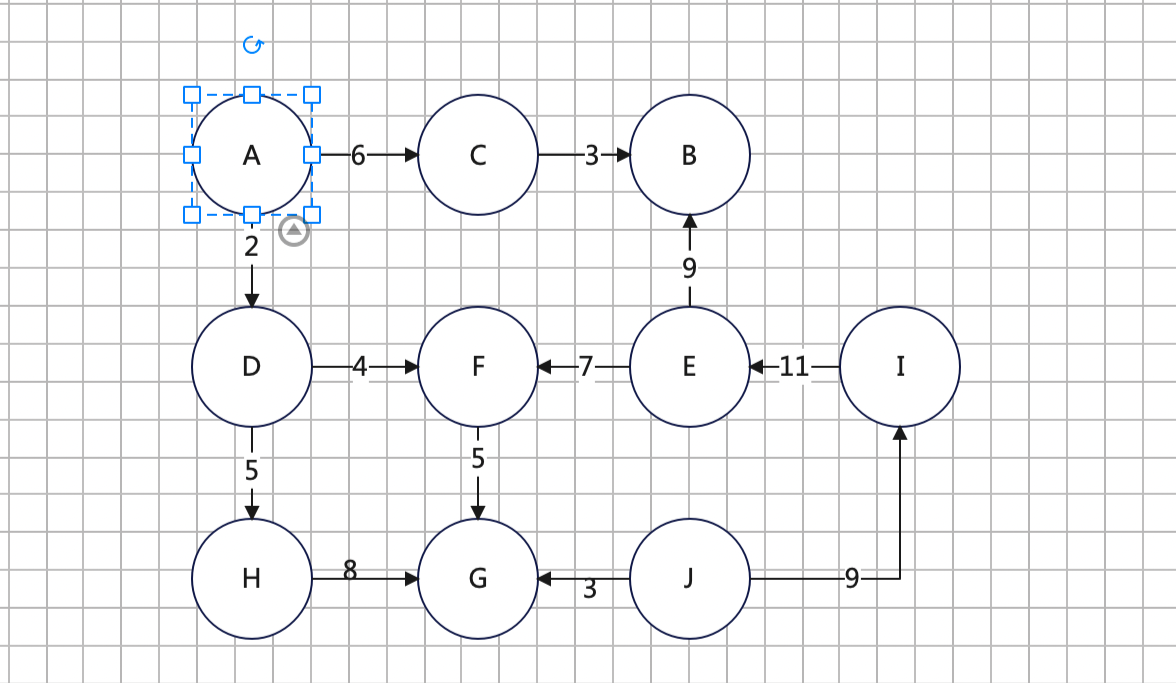
1、我们先挑选出dis中值最小的点，最开始的时候只能是源点，因为源点为0，其他点为无穷大

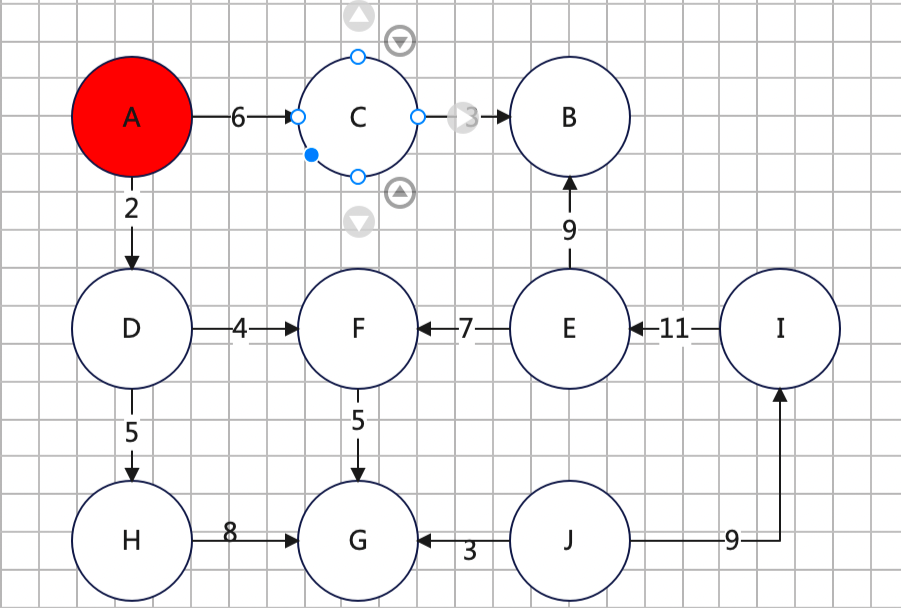
2、然后我们找到A指向的下游D、C

（1）更新C和D在dis中的值2、6，dis[D] = AD dis[C] = AC

（2）又因为AD<AC，那么D点标记为已遍历

这样也就是说A到D的最短路径已经找到了，就是AD

这里其实很容易理解这个算法的思路了，具体就是A的下游点是C、D，AC已经比AD要小，那么就算从C点继续往后，能绕回到B，也不可能比AD要小，所以AD，必然是最短路径了，后面往外扩散也是如此思路

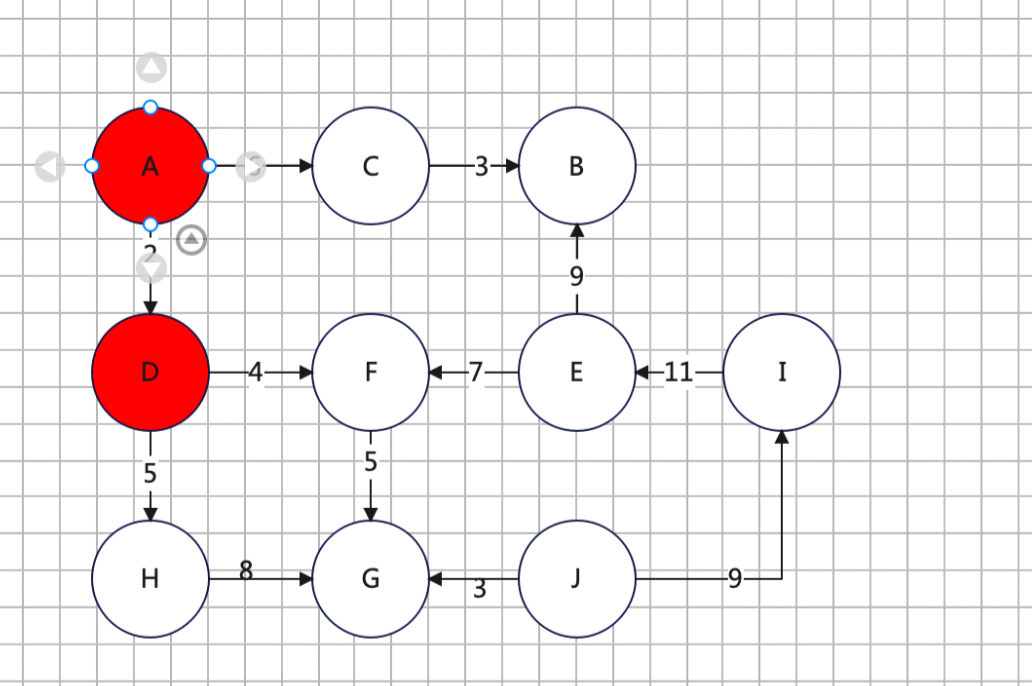
3、D的下游是H、F，更新dis[H]、dis[F]的值

（1）dis[H] = dis[D] + DH = 7

翻译一下就是A到D的最短路径 + DH

dis[F]同理 = 6

（2）又因为AC （dis[C]）= ADF（dis[F]） < ADH（dis[H]）

所以我们选择AC或者ADF都可以，这里代码里你可以写< 也可以 <=，无所谓的，假设你选择ADF，下一轮AC也会作为对比项，早晚C点都要被遍历

我们选择ADF，也就是这一次我们选择F点标记为被遍历的点

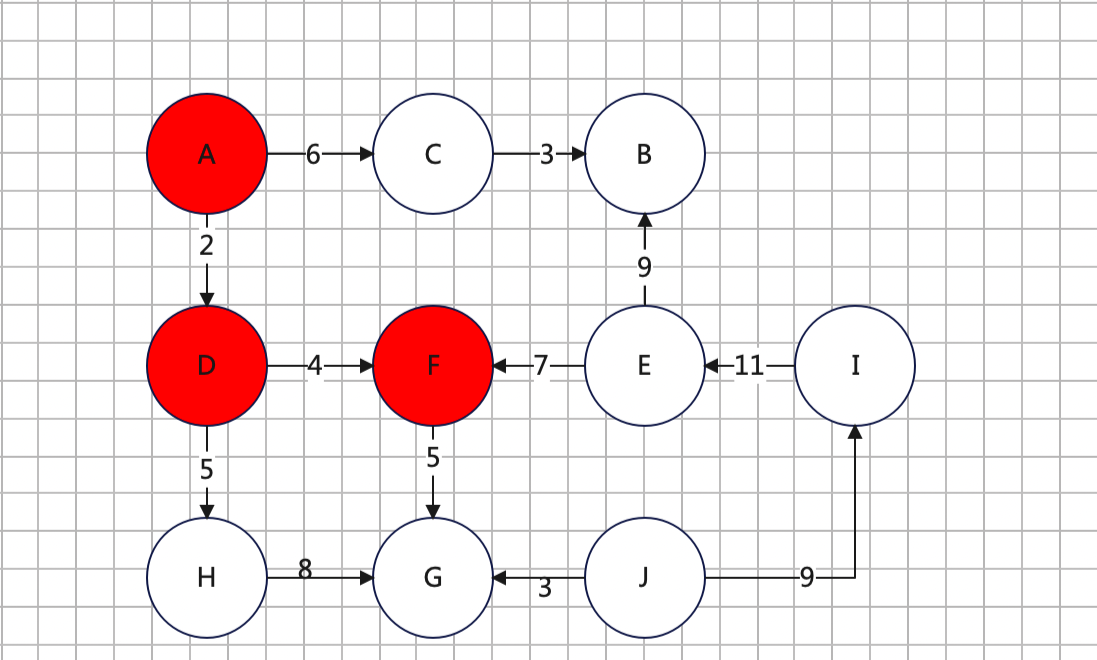
4、找到F的下游，只有G点

（1）更新dis[G]的值 dis[G] = dis[F] + FG = 6 + 5 = 11

（2）又因为AC（dis[C]） < dis[H] < dis[G]

所以这次选择将C点标记为已遍历

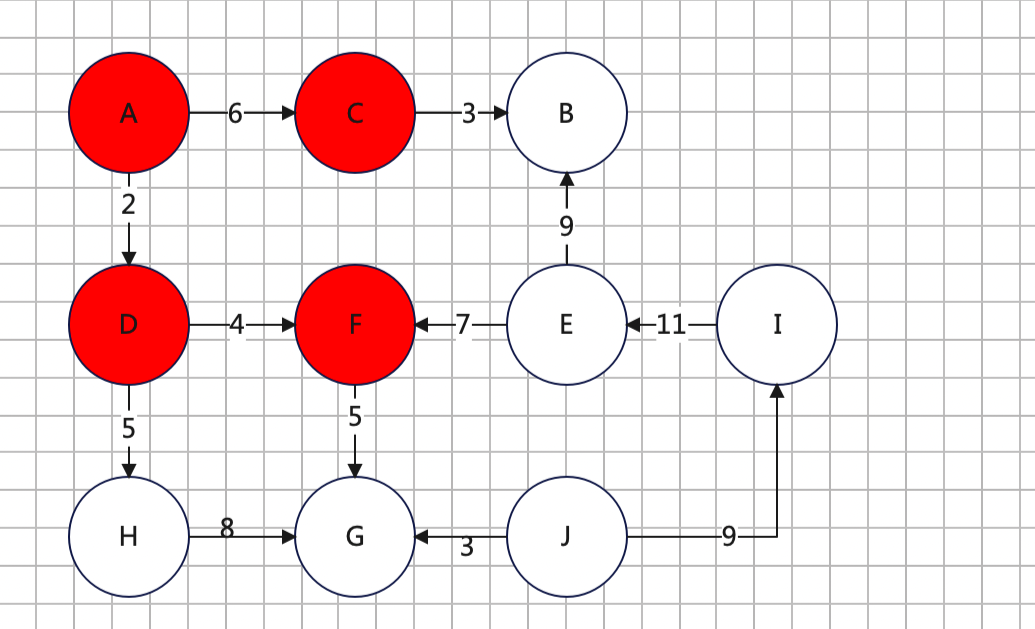
5、找到C点的下游 - B

（1）更新dis[B] = dis[C] + CB

（2）又因为dis[H] < dis[B] < dis[G]

这次选择H标记为已遍历

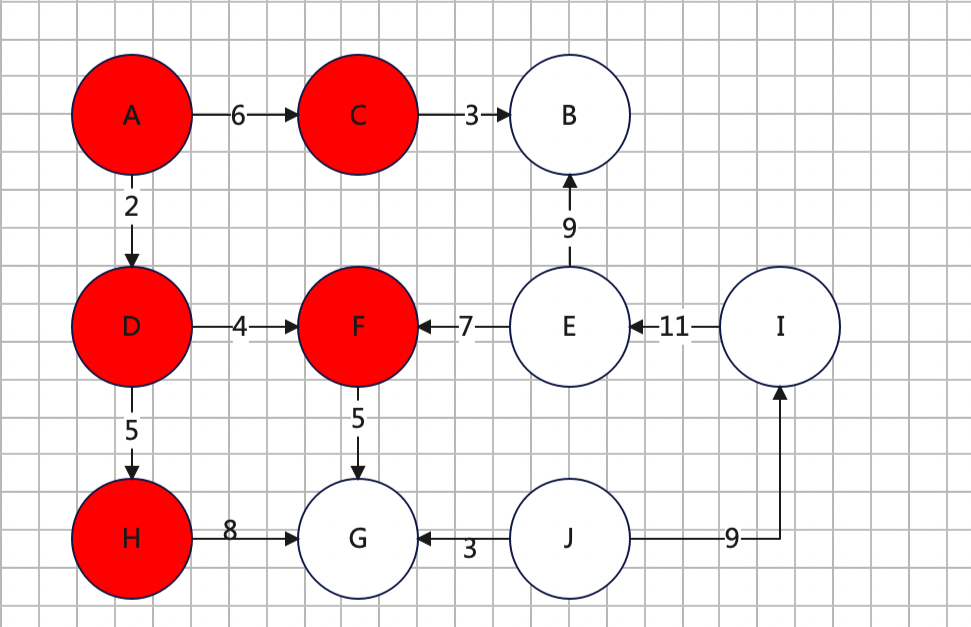
6、找到H点的下游G

（1）dis[G] 原本是 dis[F] + FG = 11，现在又有了dis[G]' = dis[H] + HG = 15，也就是说dis[G] < dis[G]' ，也就是ADHG 这个路径比 ADFG要长，所以原来的dis[G]不变还是11，

（2）又因为dis[B] < dis[G],所以下一个点选择B点标记为已遍历

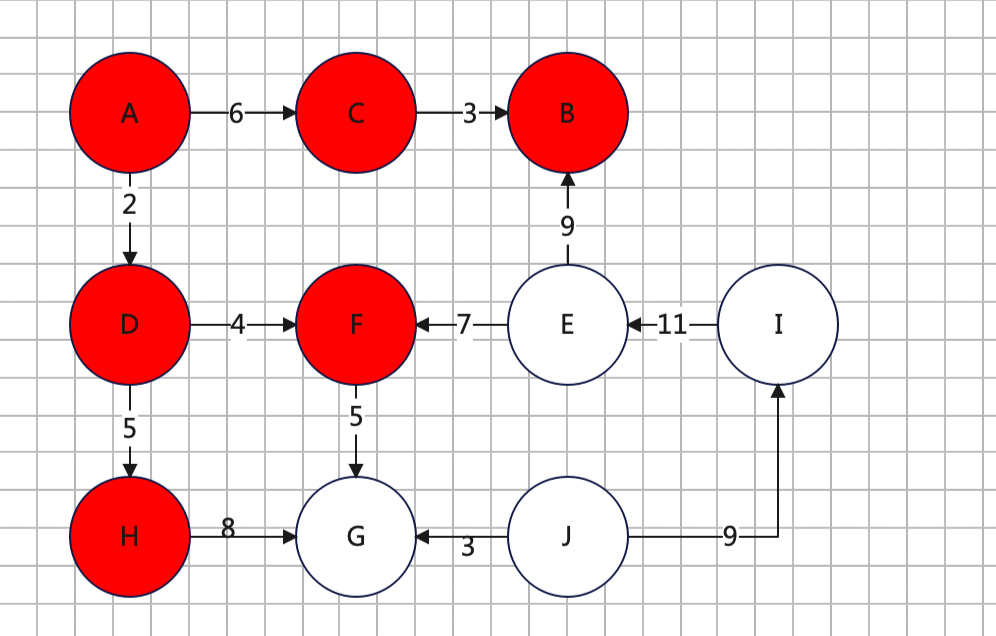
7、B没有下游，所以下一个点只能是遍历G

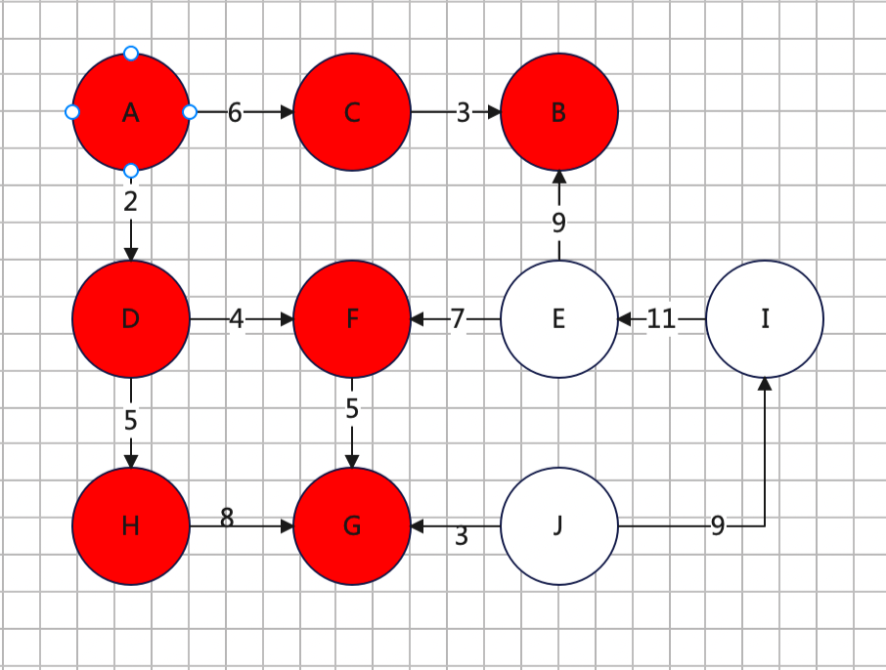
8、后面也就没什么好说的了，就一条通路，J -> I -> E

总结一下结果

点到点	最短路径	最短距离
A -> B	A ->C -> B	9
A -> C	A ->C	6
A -> D	A -> D	2
A -> E	A -> D -> F -> G -> J -> I -> E	34
A -> F	A -> D -> F	6
A -> G	A -> D -> F > G	11
A -> H	A -> D -> H	7
A -> I	A -> D -> F -> G -> J -> I	23
A -> H	A -> D -> F -> G -> J	14

代码

package main

import (
	"fmt"
	"math"
)

type Graph struct {
	dots   []string //	点
	matrix [][]int  //	邻接矩阵
}

func InitGraph(graph *Graph) error {
	graph.dots = []string{"A", "B", "C", "D", "E", "F", "G", "H", "I", "J"}
	dotsNum := len(graph.dots)
	// 建立矩阵，初始值都为0，意为，现在各个点互相不连接
	graph.matrix = make([][]int, dotsNum)
	for i := 0; i <= dotsNum-1; i++ {
		graph.matrix[i] = make([]int, dotsNum)
		for j := 0; j <= dotsNum-1; j++ {
			graph.matrix[i][j] = 0
		}
	}
	// 有向图，我们将行数字代表起点，列数字代表终点
	// A -> J 对应 0 - > 9
	// AC
	graph.matrix[0][2] = 6
	// AD
	graph.matrix[0][3] = 2
	// CB
	graph.matrix[2][1] = 3
	// DF
	graph.matrix[3][5] = 4
	// DH
	graph.matrix[3][7] = 5
	// FG
	graph.matrix[5][6] = 5
	// HG
	graph.matrix[7][6] = 8
	// GJ
	graph.matrix[6][9] = 3
	// JI
	graph.matrix[9][8] = 9
	// IE
	graph.matrix[8][4] = 11
	// EF
	graph.matrix[4][5] = 7
	// EB
	graph.matrix[4][1] = 9

	return nil
}

func ShowGraph(graph *Graph) {
	for i := 0; i <= len(graph.dots)-1; i++ {
		fmt.Println(graph.matrix[i])
	}
}

func Dijkstra(graph *Graph, originDotIndex int) {
	dotsNum := len(graph.dots)
	// 点到其他点的距离
	dis := make([]int, dotsNum)
	// 点到其他点的路径记录
	path := make([]string, dotsNum)
	// 记录点是否被遍历
	visit := make([]bool, dotsNum)

	for dotIndex := range dis {
		// 初距离为无穷大
		dis[dotIndex] = math.MaxInt
	}

	// 源点到源点的距离为0
	dis[originDotIndex] = 0
	// 源点
	path[originDotIndex] = graph.dots[originDotIndex]
	for i := 1; i < dotsNum; i++ {
		// 设置为无穷大，确保minIndex正常
		minDis := math.MaxInt
		minIndex := 0
		// 找出dis中最小的路径长度
		for disIndex := range dis {
			if dis[disIndex] < minDis && !visit[disIndex] {
				minDis = dis[disIndex]
				minIndex = disIndex
			}
		}
		// 标记被遍历
		visit[minIndex] = true

		// 更新dis
		for colIndex := range graph.matrix[minIndex] {
			if graph.matrix[minIndex][colIndex] != 0 && minDis+graph.matrix[minIndex][colIndex] < dis[colIndex] {
				dis[colIndex] = minDis + graph.matrix[minIndex][colIndex]
				path[colIndex] = path[minIndex] + graph.dots[colIndex]
			}
		}
	}
	fmt.Println(dis)
	fmt.Println(path)
	for i := range dis {
		fmt.Printf("点%s到点%s的最短路径为：%s 距离为:%v\n", graph.dots[originDotIndex], graph.dots[i], path[i], dis[i])
	}
}

func main() {
	graph := &Graph{}
	InitGraph(graph)
	Dijkstra(graph, 0)
}

输出：
[0 9 6 2 34 6 11 7 23 14]
[A ACB AC AD ADFGJIE ADF ADFG ADH ADFGJI ADFGJ]
点A到点A的最短路径为：A 距离为:0
点A到点B的最短路径为：ACB 距离为:9
点A到点C的最短路径为：AC 距离为:6
点A到点D的最短路径为：AD 距离为:2
点A到点E的最短路径为：ADFGJIE 距离为:34
点A到点F的最短路径为：ADF 距离为:6
点A到点G的最短路径为：ADFG 距离为:11
点A到点H的最短路径为：ADH 距离为:7
点A到点I的最短路径为：ADFGJI 距离为:23
点A到点J的最短路径为：ADFGJ 距离为:14