[IOI2008/BZOJ1791 岛屿](处理基环树的小技巧&基于bfs树形DP)
题目大意是在一个基环树森林里求每一棵基环树的直径①的和。
其实就是树的直径的基环树升级版。我们先把环找出来,然后从环上的每一个节点x出发,并且不经过环上其他节点,做一次树形DP,求出x的子树中到x最远的路径长d[x]和x的子树的直径dp[x]。
那么基环树的直径只有两种情况:
1.直径不经过环上的节点
对于每一个dp[x]取max就好了。
2.直径经过环上的节点
对于任意环上的两个节点x和y,都可以构成一条路径d[x]+d[y]+dist(x,y),其中dist(x,y)为x和y在环上的距离②。
可以直接n^2枚举找最大的吗?当然不能,N<=1e6耶。
这个时候就要用一点套路。首先把环复制一遍接在原先的环后,然后对dist数组做个前缀和s,那么一条路径就成了(x>y) d[x]+d[y]+s[x]-s[y]=(d[x]+s[x])+(d[y]-s[y]),也就是说对于每个x我们需要找到在x之前的一个y满足(d[y]-s[y])最大,并且x-y<=环长。单调队列优化的套路嘛!
①基环树的直径:即基环树中最长的简单路径,这里简单路径指的是不自交(不重复经过任何点或边)的路径。
②环上的距离:有顺时针和逆时针两种,因为求的是直径,所以取两者中较长的。
这是luogu的AC代码:(温馨提示:代码太丑并且不是重点,您大可直接跳过看后面)
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
typedef long long LL;
struct edge{
int v,w,last;
}e[N<<1];
int tot=1,tail[N];
inline void add(int x,int y,int z){
e[++tot]=(edge){y,z,tail[x]};
tail[x]=tot;
}
inline int read(){
int x=0,w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return w?-x:x;
}
bool incur[N];
int n,dn,cnt,dfn[N],tp,st[N][2],c[N],s[N];
void getcur(int x,int pre){
dfn[x]=++dn;
for(int p=tail[x];p;p=e[p].last)if(p^pre^1){
int &v=e[p].v,&w=e[p].w;
if(dfn[v]){
if(dfn[v]>=dfn[x]) continue;
c[cnt=1]=v,s[cnt]=w,incur[v]=true;
for(int i=tp;st[i][0]^v;--i) c[++cnt]=st[i][0],s[cnt]=st[i][1],incur[st[i][0]]=true;
}
else st[++tp][0]=v,st[tp][1]=w,getcur(v,p);
}
--tp;
}
int hd,rt,tl,q[N<<1];
LL ans,t,d[N],f[N],dp[N],sum[N<<1];
LL dfs(int x,int pre){
LL t=0;d[x]=f[x]=0;
for(int p=tail[x];p;p=e[p].last)if(p^pre^1){
int &v=e[p].v,&w=e[p].w;
if(incur[v]||v==pre) continue;
t=max(t,dfs(v,x)),f[x]=max(f[x],d[x]+d[v]+w),d[x]=max(d[x],d[v]+w);
}
return max(f[x],t);
}
LL F(int id){
return dp[id]-sum[id];
}
int main(){
n=read();
for(int i=1;i<=n;++i){
int x=read(),y=read();
add(x,i,y),add(i,x,y);
}
for(int i=1;i<=n;++i)if(!dfn[i]){
memset(sum,0,sizeof sum);
st[tp=1][0]=i,st[tp][1]=0;
cnt=0;getcur(i,0);
t=0;
for(int j=1;j<=cnt;++j) t=max(t,dfs(c[j],0)),dp[j]=dp[j+cnt]=d[c[j]];
int hd=tl=0;
for(int j=1;j<=cnt*2;++j){
sum[j]+=sum[j-1]+s[(j-1)>cnt?j-1-cnt:j-1];
while((hd^tl)&&j-q[hd]+1>cnt) ++hd;
if(hd^tl) t=max(t,F(q[hd])+dp[j]+sum[j]) ;
while((hd^tl)&&F(j)>F(q[tl-1])) --tl;
q[tl++]=j;
}
ans+=t;
}
cout<<ans<<endl;
return 0;
}
又是找环,又是树形DP,又是单调队列优化的,是不是很恶心?没错,虽然用的算法不算高级,但由于种种原因做此题的人各种RE&WA&MLE&TLE,因此在洛谷上都成黑题了。
并且我要告诉你更恶心的是,由于BZOJ栈的限制,上面这份dfs的代码在BZOJ上还会爆栈......
正是在这种山穷水尽的时候,我发现了一些黑科技。
首先我们要分析题目图的特性,这是一棵无向基环树(暂时不管森林),画出来应该是这个样子(没画边权,下同):
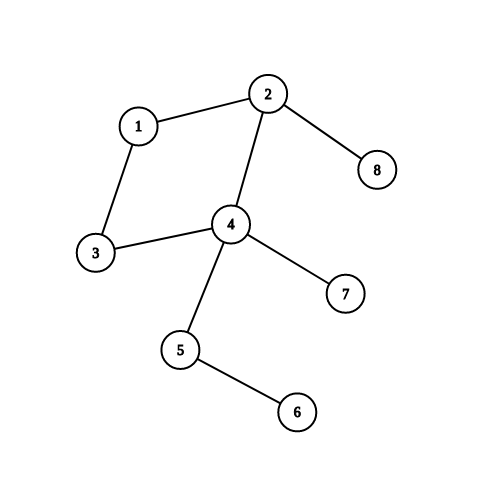
题目的输入方式有点特别,是第i+1行输入一个x和y表示i+1和x有一条长度为y的边。那么我们暂时把它当作有向边,令to[i+1]=x,w[i+1]=y,画出来就是这个样子:
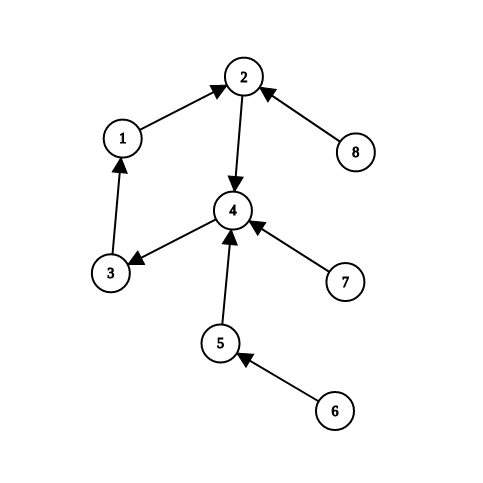
它刚好是一棵内向树③!这是巧合吗?不是的。按照这种输入方式,每个点有且仅有一条出边,连出来就一定是一棵内向树。这样一来,我们就得到了每个节点x的父亲f[x]与它到父亲的边权w[x],当然对于环上的节点是到它相邻节点的,且一定是同一个方向(有点不太好表达,看代码就懂了)。于是我们就可以用按拓扑排序的顺序自底向上地DP了,也就是基于bfs的树形DP。代码:
③内向树:n个点,n条边,每个节点有且仅有一条出边的有向连通图就好像以”基环“为中心,有向内收缩的趋势,故称为”内向树“。
#include<bits/stdc++.h>
using namespace std;
#define rg register
const int N=1e6,M=1e6+1;
typedef long long LL;
inline int read(){
int x=0,w=0;char ch=0;
while(ch<'0'||ch>'9') w|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return w?-x:x;
}
bool v[M];
int n,cnt,dcnt,cur[M<<1],to[M],w[M],in[M];
LL t,ans,s[M<<1],d[M],f[M],dp[M];
struct Deque{//这个。。。手写的双端队列,不用管它
int l,r,q[N];
Deque(){l=r=0;}
void clear(){l=r=0;}
bool empty() {return !(l^r);}
void push_back(int v) {q[r++]=v;r%=N;}
void push_front(int v) {q[l=(l-1+N)%N]=v;}
void pop_front() {++l;l%=N;}
void pop_back() {r=(r-1+N)%N;}
int front() {return q[l];}
int back() {return q[r-1];}
}q;
int main(){
n=read();
for(rg int i=1;i<=n;++i) ++in[to[i]=read()],w[i]=read();
for(rg int i=1;i<=n;++i) if(!in[i]) q.push_back(i);//入度为0的点入队
while(!q.empty()){
int x=q.front(),&fa=to[x],&l=w[x];q.pop_front();
if(!--in[fa]) q.push_back(fa);
//下面3行是DP,也就是更新父节点的信息
f[fa]=max(f[fa],d[fa]+d[x]+l); //f:x的子树中经过x节点的最长路径
d[fa]=max(d[fa],d[x]+l);//d: x的子树中离x最远的节点到x的距离
dp[fa]=max(dp[fa],max(dp[x],f[fa])); //dp:x的子树的直径,也就是对f[x]和dp[y](to[y]=x)取max
}
for(rg int i=1;i<=n;++i)if(in[i]&&!v[i]){//基环树森林,不只一个环,用v标记
cnt=0;t=0;
for(rg int j=i;!v[j];j=to[j]){//这就是上面说的,这样一直沿着to走,一定能绕环一圈
cur[++cnt]=j,v[j]=true;//把环抠下来
t=max(t,dp[j]);//上面讨论的基环树直径的第一种情况
}
dcnt=cnt<<1;
for(int i=cnt+1;i<=dcnt;++i) cur[i]=cur[i-cnt];//复制一遍环
q.clear();//注意清空
for(rg int j=1;j<=dcnt;++j){
s[j]=s[j-1]+w[cur[j-1]];//前缀和
while(!q.empty()&&j-q.front()>=cnt) q.pop_front();//使满足j-q.front()+1<=cnt
if(!q.empty())
t=max(t,d[cur[q.front()]]-s[q.front()]+d[cur[j]]+s[j]);
while(!q.empty()&&d[cur[j]]-s[j]>d[cur[q.back()]]-s[q.back()]) q.pop_back();
q.push_back(j);
}
ans+=t;//累加每一棵基环树的直径
}
printf("%lld\n",ans);
return 0;
}
于是我们仅用这么点简洁的代码就A了一道黑题!这道题告诉我:拿到题先分析题目的特性,不要一来就按照传统方式存图,找环,dfs树形DP......
2019-06-26

 浙公网安备 33010602011771号
浙公网安备 33010602011771号