Generalizable and Efficient Scene Graph Registration【IEEE TRO】
地址:https://arxiv.org/pdf/2504.14440
地址:https://arxiv.org/pdf/2504.14440
主要内容:
这项研究面向多机器人/先验地图的“对齐”问题,把环境抽象成场景图(节点=物体/语义点,边=关系),并设计网络同时编码三类信息:开放集语义、带空间感知的局部拓扑和形状特征,融合成紧凑的节点描述;前端用由粗到细的匹配找对应,后端用鲁棒位姿估计解出两图的变换,全流程保持稀疏分层表示以减少 GPU 占用与通信带宽;训练数据不依赖人工标注,而由视觉基础模型 + 语义建图自动生成;在两智能体 SLAM 基准上,配准成功率显著优于手工特征方案,相比视觉回环网络召回更高且每帧仅约 52 KB通信,代码开源,为低带宽场景下的多机器人地图对齐与共享定位提供了通用基石。

摘要—
I. 引言
在密集室内场景中进行全局配准对于视觉同步定位与建图(SLAM)系统至关重要。
它在多智能体SLAM [1]、多会话SLAM [2], [3] 以及长期SLAM [4] 系统的性能中起着关键作用。
依赖于图像匹配 [5]–[7] 进行回环检测和全局配准具有挑战性,因为图像匹配对视角差异敏感。
此外,在多智能体SLAM中,广播图像数据需要大量的通信带宽。
为了解决基于视觉的回环检测的局限性,语义辅助配准方法被提出 [8]–[10],它提供了更强的视角不变性和更高效的数据表示,从而减少了通信带宽的需求。
近年来,基于学习的语义场景图配准方法[16], [17]已经出现。
这些方法对语义场景图进行编码,并通过解决部分分配问题来确定多层次的对应关系。
它们消除了对语义节点间手工设计相似性度量的需求。
然而,当前的场景图学习方法是在带有真实标注的数据集上训练的,这导致标注数据集中的语义场景图与真实场景中的语义场景图之间存在显著领域差距,尤其是在存在噪声的情况下。
因此,这些基于学习的方法在泛化方面面临挑战,并在真实世界实验中表现出有效性有限。
这种真实世界的语义噪声和传感器噪声促使我们提出一种新的数据生成方法。
我们使用三个视觉基础模型[18]–[20]和一个语义建图模块:FM-Fusion [11]来重建语义场景图。
在真实室内环境中,与使用Mask R-CNN [21]结合早期语义建图方法[22], [23]生成的场景图相比,重建的语义场景图展现出更高的质量。
尽管我们的方法有效地将语义噪声限制在适当水平,但它不能完全消除噪声。
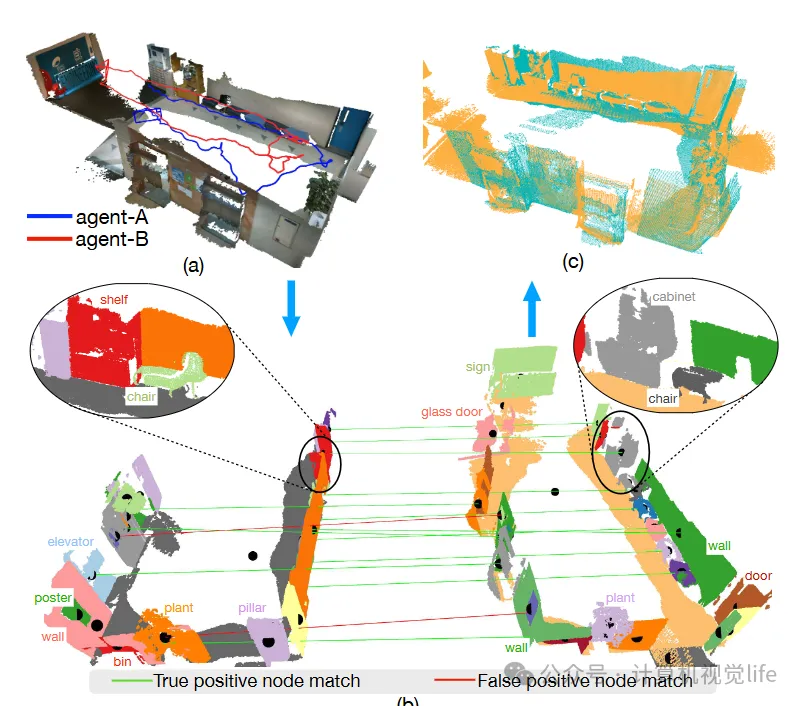
例如,如图1所示,来自两个场景图的放大子体积揭示了由于真实世界重建中的噪声而导致的语义不一致。
与先前依赖真实语义标注生成数据的场景图学习方法[16], [17]相比,我们的方法引入了一个新的实际挑战。
II. 相关工作
A. 图像配准
B. 点云配准
C. 场景图构建
D. 语义数据关联
III. 预备知识
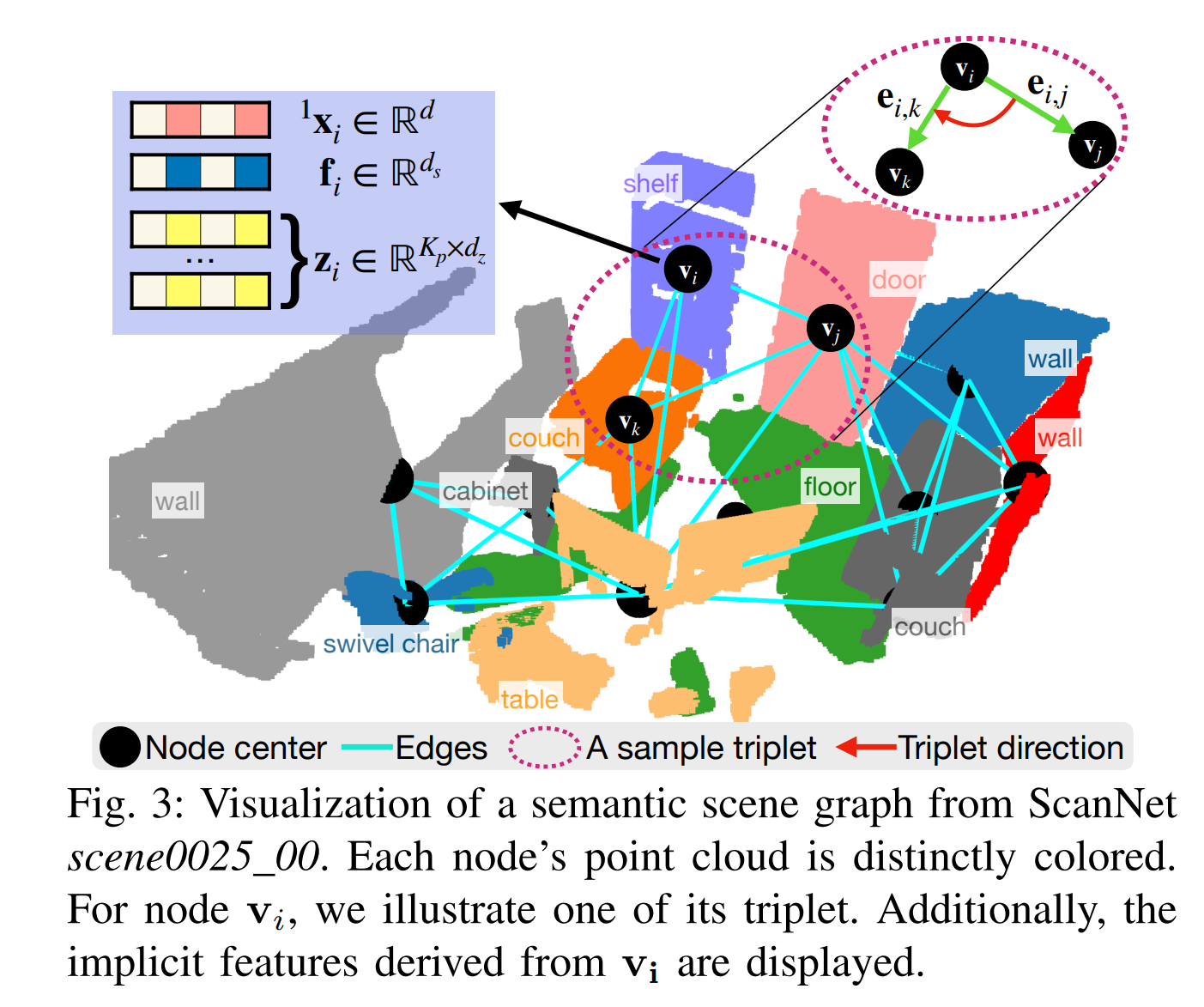
- 显式表示:我们将语义场景图表示为 G = {V, E},其中 V 是节点集,E 是边集。一个语义节点 v_i 具有以下属性:
- s 是其文本格式的开放集语义标签。
- b ∈ R³ 表示其边界框的长、宽、高。
- o ∈ R³ 是其几何中心。
- P 是其点云。
- 隐式表示:它融合了多种模态的信息。
- 语义特征 (f_sem):通过预训练的语言模型(如BERT)从文本标签
s编码得到的高维向量,用于捕获语义信息。 - 拓扑特征 (f_topo):通过图神经网络(GNN)聚合节点自身及其邻域节点的信息(如位置、语义)得到的特征,用于描述节点在场景图中的局部结构关系。
- 形状特征 (f_shape):从节点的点云
P中提取的特征,用于描述物体的几何形态。
- 形状特征:fi∈Rds,其中 ds是形状特征的维度。
- 节点特征:lxi,其中 l是层索引。在形状网络之前,节点特征为 0xi∈Rd或 1xi∈Rd(需根据上下文确认初始层)。与形状特征融合后,最终的节点特征为 2xi∈Rd+ds。
- 点特征:zi∈RKp×dz,其中 Kp是采样点的数量,dz是点特征的维度。
- 符号约定:我们使用小写符号表示单个节点的特征,大写符号表示整个场景图的特征。例如,2xi是一个节点特征,而 2XA是来自场景图 GA的所有节点特征堆叠后的集合。

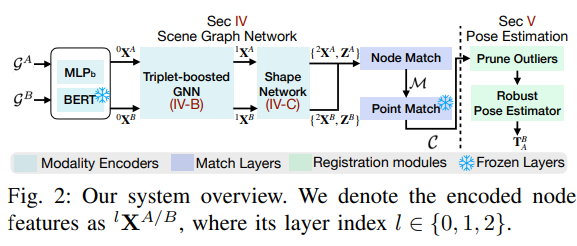
IV. 场景图网络
A. 语义场景图构建
语义场景图使用 FM-Fusion [11] 构建。我们提取其语义实例并构建场景图中的语义节点集 V。
那些过小或观测不足的实例会被排除。
对于一个节点 v,其语义标签 s 来自 FM-Fusion 的预测结果。
该节点可能被 GroundingDINO 多次观测到,FM-Fusion 会融合多次标签测量值来预测最终标签 s。
点云 P 通过 3D 插值从实例级的子图中提取。
此插值过程类似于移动立方体法 [59],但仅对拥有三个相邻体素的点进行插值。
我们从 P 中提取节点中心 o。
随后,使用 O'Rourke 算法 [60] 根据 P 计算最小包围盒。
记录包围盒形状 b ∈ R³,代表其长、宽、高。
我们忽略每个语义节点的方向以避免引入额外噪声。
最终,构建一个语义节点 v = {s, b, o, P}。
我们为其他节点构建相应表示并生成节点集 V。
一旦节点集 V 构建完成,我们计算每对节点之间的距离。
该距离可根据节点中心计算。
如果距离小于阈值 τ_d,则在它们之间连接一条边。
距离阈值 τ_d 由节点的形状大小决定,这意味着较大的节点会连接到更远距离的节点以及更多数量的节点。
我们记录生成的边集 E。
如图 3 所示,我们可视化了一个场景图 G = {V, E} 的示例。

/输入的语义场景图 {G^A, G^B} 之间存在 4 自由度的相对变换,包括 3D 位置和相对偏航角旋转。
横滚角和俯仰角的相对旋转已由视觉-惯性 SLAM [31] 准确估计.
B. 三元组增强的图神经网络(GNN)

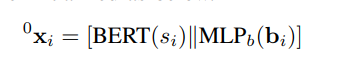
其中 0xi∈Rd,[⋅∥⋅]表示向量拼接。

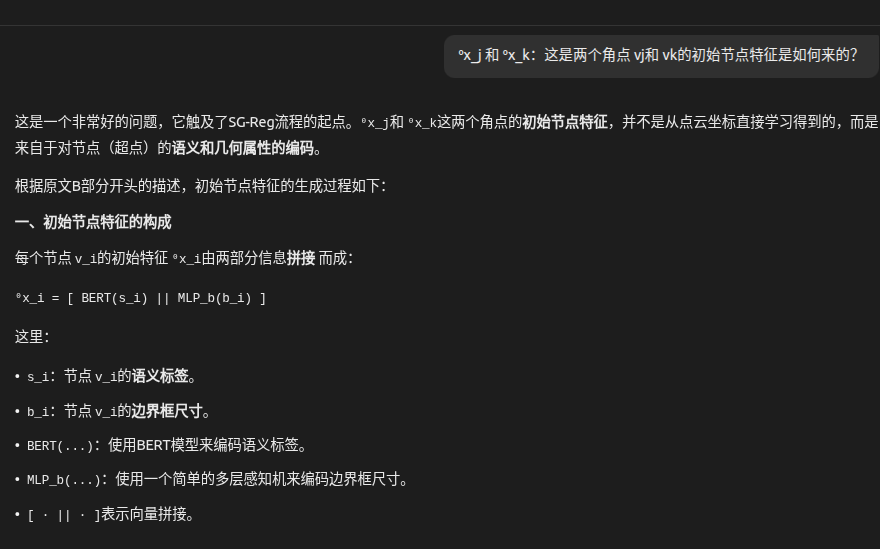



=======================

1. 三元组的定义
如图所示,一个三元组由三个节点构成:
- 锚点:一个语义节点
vi。 - 两个角点:从锚点的邻居节点中随机采样两个节点
{vj, vk}。
2. 关键设计:顺序不变性以实现旋转不变性
这是实现旋转不变性的最精妙设计。为了保证无论点云如何绕Z轴旋转,同一个三元组都能被编码成相同的特征,作者强制规定了一个固定的角点顺序。
- 规则:两个角点
vj和vk按照绕Z轴逆时针方向 的顺序排列。 - 数学实现:通过计算向量叉积的Z分量
(ei,j × ei,k)z来判断顺序。- 如果
(ei,j × ei,k)z ≥ 0,说明从ej到ek是逆时针(或共线),则顺序为(j, k)。 - 如果
(ei,j × ei,k)z < 0,说明是顺时针,则顺序应交换为(k, j)。
- 如果


3. 三元组特征的构成
一个有序三元组 (vi, vj, vk)的特征 t_i^{j,k}由三部分拼接而成:
t_i^{j,k} = [⁰x_j || ⁰x_k || g_i^{j,k}]
- ⁰x_j 和 ⁰x_k:这是两个角点
vj和vk的初始节点特征。这些特征包含了角点的语义和边界框尺寸信息(通过BERT和MLP编码)。这为三元组注入了语义信息。 - g_i^{j,k}:这是三元组的几何嵌入,编码了三角形的几何形状。
g_i^{j,k} = [ψ_L(|e_i,j|) || ψ_L(|e_i,k|) || ψ_A(ê_i,j · ê_i,k)]|e_i,j|,|e_i,k|:两条边的长度(标量)。ê_i,j · ê_i,k:两条边单位向量的点积,等价于夹角θ的余弦值cos(θ)(标量)。ψ_L和ψ_A:正弦化函数。这是一种将标量值映射到高维空间的标准方法,能使神经网络更好地学习连续值之间的规律。这使得特征对边的长度和角度的微小变化不敏感,增强了鲁棒性。


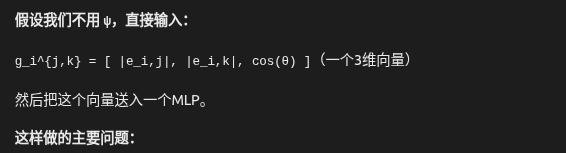





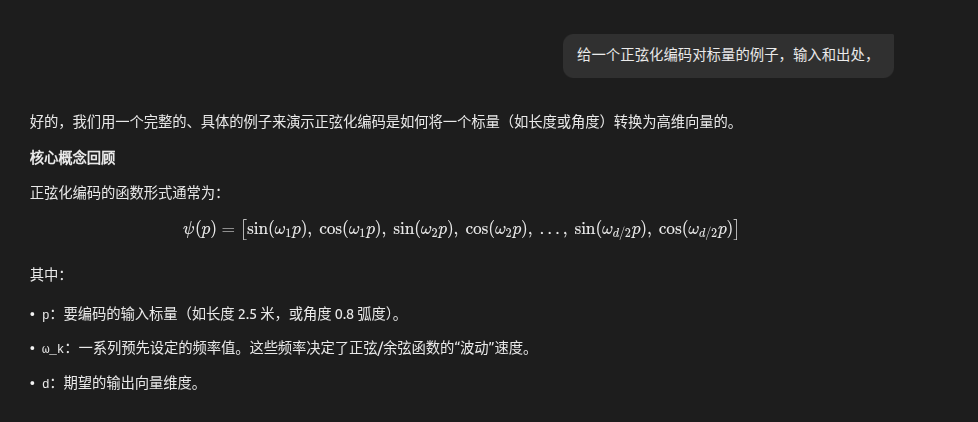



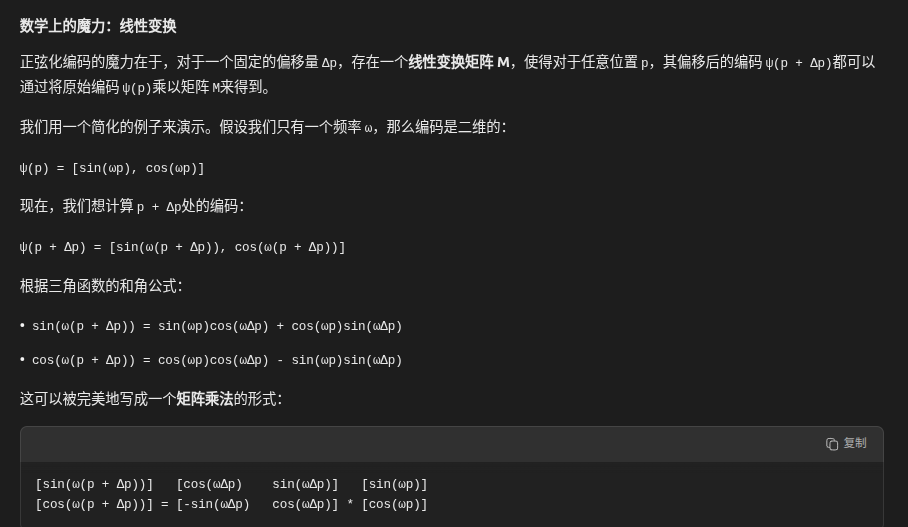



=================================



三、将三元组描述符集成到GNN中
传统的GNN通过聚合邻居节点j的特征来更新锚点i的特征。SG-Reg的创新在于,它不直接聚合单个邻居,而是聚合以锚点为中心的一个个三元组结构。
1. 消息计算
对于锚点 vi,从其所有关联的边中采样一组三元组 (j, k)。聚合的消息 mi计算如下:m_i = Σ_{(j,k)} α_i^{j,k} * (W_V * t_i^{j,k})
W_V:一个可学习的线性投影层,用于将三元组特征t转换为"值"。α_i^{j,k}:注意力权重。这个权重表示三元组(j,k)对于描述锚点vi的重要程度。
2. 注意力权重的计算
注意力权重 α通过标准的注意力机制计算:α_i^{j,k} = softmax_{i} ( (W_Q * t_i^{j,k}) · (W_K * t_i^{j,k})^T )
W_Q,W_K:可学习的线性投影层,用于将三元组特征t分别转换为"查询"和"键"。- 这里的一个关键是,查询和键来自同一个三元组描述符。这意味着,模型是在学习一个三元组自身的内在重要性,以及它对于描述锚点上下文的相关性。
3. 节点特征更新
最后,用聚合自所有相关三元组的消息来更新锚点 vi的特征:¹x_i = ⁰x_i + MLP( [⁰x_i || m_i] )
⁰x_i:锚点vi的初始特征(残差连接)。[⁰x_i || m_i]:将初始特征与聚合的三元组消息拼接。MLP:一个多层感知机,用于融合自身信息和上下文消息。
通过这种方式,每个节点的最终特征 ¹X不再是孤立的,而是注入了其周围局部拓扑结构(以三元组形式)的丰富上下文信息。
四、优势总结(对照原文)
- 优于普通GAT:相比普通的图注意力网络,三元组描述符极大地增强了GNN的空间结构感知能力。模型不再只看相邻节点,而是看相邻节点构成的几何结构。
- 优于带RPE的GNN:最关键的是,它解决了RPE的旋转敏感性问题,确保了学习到的特征对偏航角旋转具有不变性,这对于跨场景的泛化至关重要。
- 符合人类直觉:作者用了一个生动的例子:人类描述办公室布局时会说“一张沙发面朝电视机,并且它的左边有一张桌子”。这正是一个典型的三元组描述(锚点:沙发,角点:电视机和桌子)!SG-Reg的三元组描述符就是在数学上模拟这种人类的空间认知方式。
- 对噪声鲁棒:即使在场景图存在噪声(如节点缺失、错误)的情况下,只要一个节点的特征聚合到了一两个正确的三元组信息,它仍然有很高的概率被正确匹配。因为三元组是一个相对稳定的局部结构。
结论:Triplet-boosted GNN 是SG-Reg的灵魂。它通过一种巧妙且符合直觉的方式,将旋转不变的局部拓扑结构信息注入到节点特征中,从而实现了强大且泛化能力强的场景图匹配。
当前的注意力GNN在其自注意力聚合机制中引入了相对位置编码(RPE)[7]:
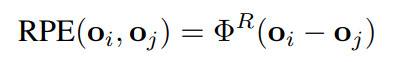
其中 oi/j是节点中心,ΦR是一种旋转编码。RPE已被证明在视觉任务[7][61]和语言任务[24]中能增强学习效果。
然而,RPE在3D几何任务中存在一个关键局限:
它对偏航角旋转不具有不变性。
具体而言,当输入图经历偏航角旋转变换时,RPE无法产生旋转不变的特征,而这在此类场景的鲁棒匹配中至关重要。
为解决这一挑战,我们设计了一种三元组描述符来增强GNN的学习能力。
该三元组描述符被设计为对4自由度全局变换具有不变性。
如图3所示,我们将语义节点 vi∈VA设为三元组的锚点,并随机采样其两个相邻节点 {vj,vk}作为三元组的角点。
三元组特征记为 (t^i_{j,k} \。
在计算 tj,ki时,我们按照视觉SLAM坐标系[31]中沿z轴的逆时针方向保持角点节点 vj, vk的顺序。
数学上,三元组特征定义如下:
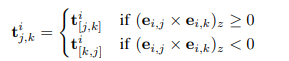
首先定义相对位置向量 ei,j=oj−oi,其中 oi和 oj分别为节点 vi和 vj的几何中心坐标。
然后计算有序三元组特征:
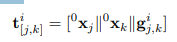
g<sup>i</sup><sub>j,k</sub> 是一个几何嵌入,它通过一个多层感知机(MLP)将三元组特征映射到高维空间:
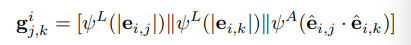
其中,三元组边的长度 ∥ei,j∥,∥ei,k∥∈R,而 e^i,j,e^i,k是归一化后的向量。
项 e^i,j⋅e^i,k表示三元组夹角的余弦值。正弦函数 ψL和 ψA分别用于嵌入边长度和三元组角度。
这些正弦函数在 GeoTransformer [41] 中曾被用于编码几何标量。
在阐述了三元组特征的构建过程后,我们现在说明如何将其集成到 GNN 中。
三元组增强的 GNN 读取初始化的节点特征 0XA并输出为 1XA。
对于所有 i∈A,残差消息传递的更新过程如下:
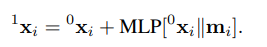
为为计算消息特征 mi,我们首先从其关联的边集 E(i,⋅)中采样一组三元组。随后利用注意力机制 [46] 计算该特征,该机制聚合了所有采样三元组的嵌入。
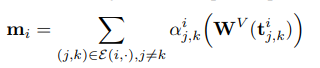
注意力得分 α<sup>i</sup><sub>j,k</sub> 通过对所有查询-键相似度进行softmax计算得到:
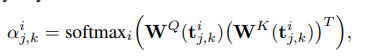


与普通的图注意力网络[25]相比,三元组增强了GNN的空间感知能力。
与结合了RPE[7]的GNN相比,我们的方法确保了特征对偏航旋转保持不变性。
此外,我们的过程更贴近人类直觉。
人类通过具有空间感知的物体拓扑来描述房间布局以识别之。
例如,一个人可能会描述他办公室里的沙发面朝电视机,并且其左侧有一张桌子。
我们的三元组描述符通过空间感知捕捉局部拓扑,模拟了人类直觉。
在SLAM领域,虽然已有类似的三元组描述符[62]–[65]被提出,但它们是以显式方式表示三元组的。
我们认为,在我们所针对的跨域场景中,三元组是一种相对稳定的局部结构。
即使在有噪声的场景图下,如果一个节点特征聚合了一个或两个正确的三元组,它仍然有很大可能找到正确的匹配。
C. 形状网络
好的,我们结合原文详细讲解SG-Reg中形状网络的设计思想、具体架构和工作流程。这部分的核心目标是提取能够描述每个语义节点(超点)自身精细几何形状的特征。
一、核心思想与动机
形状网络的目标是为场景图中的每个节点(对应点云中的一个物体或一个局部区域)生成一个强大的几何特征。这个特征需要描述该节点所代表区域的详细3D形状。
- 为什么需要形状网络?
- 补充拓扑信息:之前的Triplet-boosted GNN主要捕捉的是节点之间的拓扑关系(相对位置)。形状网络则专注于节点内部的几何信息(自身形状)。两者结合,形成了“内在几何”与“外在关系”的互补。
- 提供精细的几何判别能力:两个拓扑关系相似的节点(比如都是“椅子左边有桌子”),如果它们的形状差异巨大(一个是办公椅,一个是沙发椅),仅靠拓扑特征可能无法区分。形状特征提供了关键的局部判别依据。
- 设计上的独特优势(与传统点云配准方法对比):
- 效率高:传统方法(如GeoTransformer)直接在密集的点云特征上计算注意力,内存消耗巨大。SG-Reg先通过形状网络将密集的点特征聚合为稀疏的节点级形状特征,极大降低了后续图匹配的计算复杂度。
- 特征紧凑:最终每个节点只有一个形状特征向量
F_A,可以很方便地与GNN输出的拓扑特征等进行融合,形成统一的、紧凑的节点描述符。 -



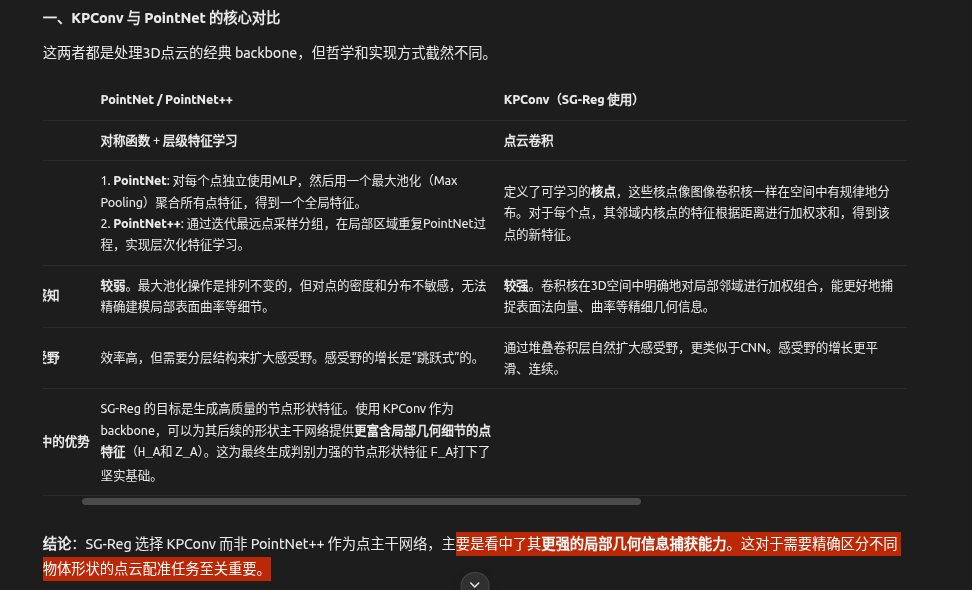

二、SG-Reg 形状编码器 vs. SG-PGM 编码器
这个对比更能体现 SG-Reg 在架构设计上的创新。
SG-PGM 的形状特征提取
SG-PGM 是场景图配准领域的另一篇重要工作。它通常采用一种更直接或传统的方式来获取节点的形状特征:
- 特征来源:通常直接使用现成的、在大型数据集(如ScanNet)上预训练好的点云分割网络(如 PointNet++ 或 SparseConvNet)的特征。
- 提取方式:
- 将整个场景输入网络,获得每个点的特征。
- 对于每个节点(超点)所覆盖的区域,直接对其内部所有点的特征进行平均池化 或 最大池化,从而得到一个固定维度的节点形状特征。
- 特点:
- 简单有效:实现起来非常简单,不需要额外的复杂模块。
- 依赖预训练:节点形状特征的质量严重依赖于预训练模型的好坏和泛化能力。如果目标领域与预训练数据差异很大,性能可能下降。
- 特征可能不够专注:预训练模型是为整个场景的分割或分类设计的,其特征可能没有针对“描述一个独立物体的完整形状”进行优化。
SG-Reg 的形状编码器(形状主干网络)
SG-Reg 专门设计了一个形状主干网络来生成形状特征,这是一个更精细、更专注的设计:
- 特征来源:基于自己定制的点主干网络(KPConv)提取的、多分辨率的点特征。
- 提取方式:
- 节点中心化处理:首先根据节点索引,将属于每个节点的点云和其特征采样并规范化(固定点数量
K_p)。这个操作本质上是将每个节点代表的局部区域独立出来进行处理。 - 专用编码器-解码器:使用一个轻量级的网络(可能基于PointNet或Transformer)来专门学习如何聚合一个节点内部的点特征。这个编码器是为形状描述任务量身定制的。
- 自监督信号:通过解码器重构点特征,为形状编码器的学习提供了强大的密集监督信号,迫使它学习到的形状特征
F_A必须包含足够的信息来还原节点的详细几何形态。
- 节点中心化处理:首先根据节点索引,将属于每个节点的点云和其特征采样并规范化(固定点数量

================================================================
形状网络生成两个层级的几何特征。
它包含一个学习点特征的点云骨干网络,以及一个学习节点级形状特征的形状骨干网络。
给定一对场景图 {G^A, G^B},我们提取它们的全局点云 {X, Y},其中每个点都标注了其所属的父节点索引。
我们将这些点云下采样为四个分辨率 {^lX, ^lY}_l,其中层索引 l = {0, 1, 2, 3}。在下采样过程中,父节点索引保持不变。
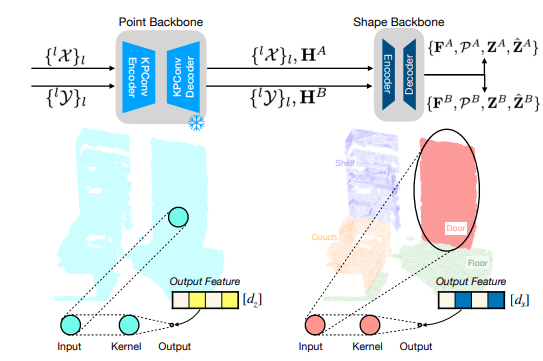
图4:形状网络结构及其点聚合核的可视化。
点云骨干网络使用网格下采样来决定聚合核,这些核小而密集。
形状骨干网络遵循实例分割来创建聚合核,这些核大而稀疏。
在接下来的步骤中,我们以 {^lX}l 的编码为例进行说明,{^lY}l 的处理方式与之相同。
如图4所示,点云骨干网络在多个层级生成点特征。
我们仅将第二精细层级的点特征作为隐藏状态特征 H^A 使用。
我们没有采用最精细层级的点云特征,因为正如先前工作[41]所指出的,这些特征是冗余的。
利用在 ^1X 中维护的节点索引,我们可以直接从 H^A 中采样节点级别的点。
在采样过程中,我们仅为每个节点保留 K_p 个点。
如果某个节点的点数量过少或过多,我们通过随机采样或零填充将数量调整至 K_p。
采样得到的节点级点云和特征分别记为 P^A 和 Z^A。

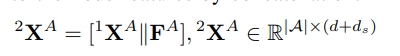
D. 分层图匹配
通过学习得到的节点特征及其点特征,我们可以运行分层图匹配层来搜索对应关系。如表II所示,我们总结了节点分配矩阵 AX和点分配矩阵 AZ。解码后的点分配矩阵 A^Z用于监督形状网络的训练,在推理过程中会被跳过。
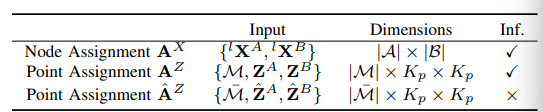
接下来,我们阐述每个层级分配矩阵的构建。
在先前的工作中,SuperGlue [6] 将图匹配问题表述为一个可微分的部分分配问题,并通过 Sinkhorn 算法 [26] 确定最优匹配。
我们在图匹配中采用了类似的技术。在节点匹配层,我们按如下方式计算节点相似度矩阵和节点分配矩阵:


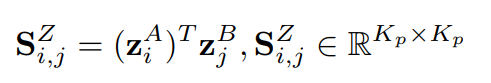

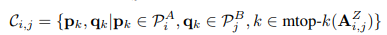

E. 训练
1) 损失函数: 我们按如下方式训练网络:
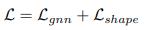
提出 L_gnn 是为了监督三元组-GNN 和节点匹配层,而提出 L_shape 是为了监督形状骨干网络。
具体而言,
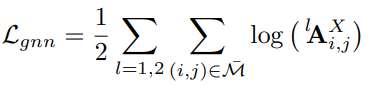

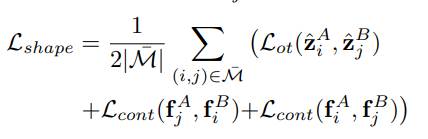
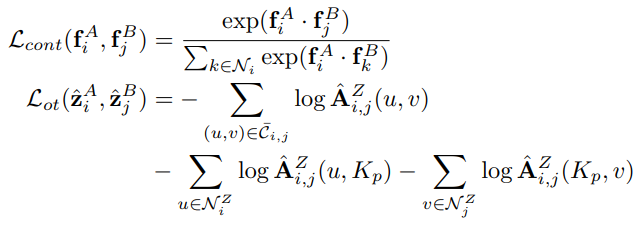

V. 鲁棒位姿估计器

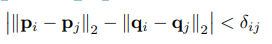



尽管上述框架在应对极低内点率配准时表现出色,但在处理较高内点率和重复对应模式时,其效率和鲁棒性可能会受到影响。
为解决这些局限性,我们引入了两种实用策略,旨在同时提升系统的效率和鲁棒性。
首先,虽然最大团剪枝法[69]在低内点率下展现出卓越的鲁棒性,但其计算成本在实践中随内点率线性增长。
相比之下,GNC在较高内点率下能提供相当的精度且执行更快。
因此,我们的混合方法仅在GNC估计的内点率低于某个特定值(例如0.3)时才激活最大团剪枝。
否则,我们直接采用GNC的预测结果作为候选变换。该策略实现了最优的速度-精度权衡。
其次,重复结构容易产生密集且内部一致的点对应关系,这可能形成一个大的异常值团,从而使基于最大团的内点选择策略[38]失效。
为缓解此问题,我们对对应关系应用非极大值抑制。
对于对应关系 (pi,qi)和 (pj,qj),如果 ∥pi−pj∥22小于预设阈值,我们仅保留得分较高的那个对应关系。
异常值剔除和鲁棒位姿估计器不存在泛化问题。它们保证了在可能具有高异常值率的跨域评估中的配准性能。
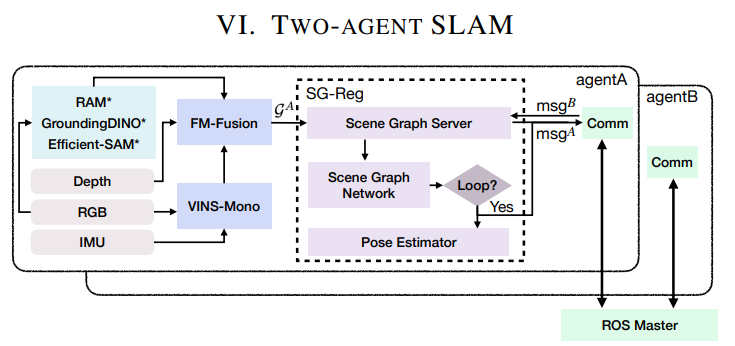
为展示场景图配准如何助力SLAM任务,我们将SG-Reg集成至一个双智能体SLAM系统中,用于检测回环并对场景图进行配准。所实现系统的结构如图5所示。
1) 由粗到精的通信: 我们引入一种由粗到精的通信策略,以实现精度与通信带宽间的最佳平衡。
- 初始阶段,每个智能体以稳定频率(例如1 Hz)广播其粗粒度消息,使SG-Reg能够匹配语义节点。
- 在某个查询帧,如果匹配的节点数达到最小值,该智能体会向远程智能体发送请求消息。
- 作为响应,远程智能体会发布稠密消息,使得请求方智能体能够执行图2所示的完整配准流程。
- 为防止稠密消息发布过于频繁,我们在允许发送请求消息的查询帧之间设定了最小时间间隔。
为展示场景图配准如何助力SLAM任务,我们将SG-Reg集成至一个双智能体SLAM系统中,用于检测回环并对场景图进行配准。所实现系统的结构如图5所示。
1) 由粗到精的通信: 我们引入一种由粗到精的通信策略,以实现精度与通信带宽间的最佳平衡。
- 初始阶段,每个智能体以稳定频率(例如1 Hz)广播其粗粒度消息,使SG-Reg能够匹配语义节点。
- 在某个查询帧,如果匹配的节点数达到最小值,该智能体会向远程智能体发送请求消息。
- 作为响应,远程智能体会发布稠密消息,使得请求方智能体能够执行图2所示的完整配准流程。
- 为防止稠密消息发布过于频繁,我们在允许发送请求消息的查询帧之间设定了最小时间间隔。
下方我们重点说明来自智能体A的广播消息格式:
- 粗粒度消息:
{X^A, O^A} - 稠密消息:
{X^A, O^A, X}
其中,节点特征 XA∈R∣A∣×d,节点中心点 OA∈R∣A∣×3,而堆叠的点云 X如第四章节C节所述。
为提升接收粗粒度消息时的性能,我们在程序中维护了最新的点对应关系 C~。
当收到粗粒度消息时,如果 C~可用,我们会将匹配节点的中心与 C~合并来构建最终对应关系集 C;
否则,仅使用匹配节点的中心构建 C。
每次读取 C后,SG-Reg会在没有初始变换的情况下预测一个全局变换 TBA。
2) SG-Reg部署: 我们使用 LibTorch 实现了SG-Reg中的网络模块,从而能够从C++可执行程序中调用神经网络。
我们将SG-Reg与其他SLAM模块集成。
SG-Reg中的每个网络块被独立部署,允许SLAM系统在融合或不融合形状特征的情况下匹配语义节点。
3) SLAM集成: 如图5所示,我们使用 VINS-Mono [31] 计算视觉-惯性里程计。
RAM-Ground-SAM [18], [19], [70] 处理RGB序列并在实验前保存其预测结果。
FM-Fusion [11] 读取来自RAM-Ground-SAM的预备数据并实时运行。
VII. 实验
我们进行了一系列实验来评估我们的方法。
这些实验揭示了我们的方法具有以下优势,这些优势与我们在第一章中声明的创新点相符:
- 场景图匹配:通过第七章节D部分讨论的三元组增强GNN和形状特征融合,实现了性能提升。
- 泛化能力:我们的方法的配准能力在跨域数据集(第七章节C部分)和真实世界SLAM系统(第七章节E部分)中得到了验证。
- 高效性:编码稀疏场景表示在第七章节C部分中所需GPU资源显著减少,在第七章节E部分中提升了通信效率,并在第七章节F部分中加快了推理速度。
- 自监督训练:我们在第七章节A(4)部分阐述的训练方法,涉及从已配准的RGB-D序列自动生成数据。
- 节点召回率(NR)和节点精确率(NP):
- 用于评估场景图匹配性能。如果节点点云之间的交并比(IoU)高于阈值 τiou=0.3,则视为真正例(TP)节点对,否则为假正例(FP)对。
- 然后,我们可以计算NR和NP,类似于图像匹配任务[6]中的召回率和精确率。
- 配准任务指标:遵循GeoTransformer[41],使用内点率(IR)和配准召回率(RR)来评估精度。
- 根据预测的变换,如果对齐点云之间的均方根误差(RMSE)小于阈值(例如,RMSE < 0.2m),则认为该预测是一次成功的配准。配准召回率是成功配准的比例。
3) 基线方法:
我们将配准性能与 SG-PGM [17] 和 GeoTransformer [41] 进行比较。
在双智能体 SLAM 中,我们的方法与 Hydra [15], [50] 和 HLoc [30] 进行对比。
Hydra 和 HLoc 在基准测试中以离线方式运行。
4) 训练数据: 在 ScanNet-Mapping 数据中,每个 ScanNet 序列被分割成多个子序列。
我们选择一对子序列分别作为源序列和参考序列。
每对场景图都施加了一个随机的 4 自由度变换。
我们在每个子序列上运行 FM-Fusion。
因此,我们可以获得大量用于训练和评估的场景图对。
由于未使用 ScanNet 的真实标注,我们声称我们的方法采用了自监督的场景图训练。
该训练方法可以扩展到其他室内 RGB-D SLAM 数据,并且不需要真实的语义标注。
在 3RScan-GT 数据中,我们直接应用了 SGAligner [16] 的数据生成方法。
5) 实现细节: 我们使用 Adam 优化器训练网络,学习率为 0.01。
训练数据包含 1990 对从 ScanNet-Mapping 和 3RScan-GT 数据集重建的场景图。
形状网络的预训练进行 64 个周期,其余训练进行 80 个周期。
我们在配备 Intel-i7 CPU 和 Nvidia RTX-3090 GPU 的台式计算机上运行训练过程和所有实验。
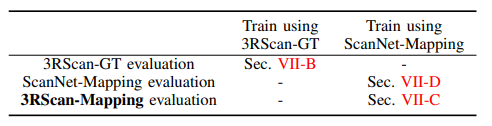
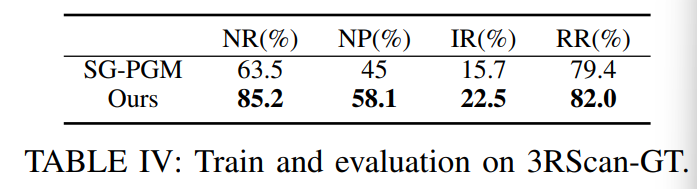
B. 3RScan 基准测试
本节旨在评估不同方法在使用完全精确的训练和验证标注时的精度差异。我们使用官方发布的版本。
我们对训练好的SG-PGM模型进行了两处调整。
首先,我们使用BERT对其语义标签进行编码,这与我们的方法相同。
SG-PGM的原始版本是从其每个语义标签生成语义直方图,并构建语义特征向量。
由于BERT是更强的语义编码器,我们将其应用于SG-PGM以确保公平比较。
其次,SG-PGM会读取边的关联关系标签。
我们将所有关联关系标签都设为"无"。
这是因为3RScan-Mapping中的场景图不提供任何关联关系标签,因此我们在两个版本的训练中均将其设置为"无"。
C. 跨域基准测试
深度学习方法常常受限于其泛化性能。
考虑到我们的方法旨在应用于机器人的长期使用,我们认为有必要评估其跨数据集的性能。
在本节中,我们详细评估了我们的方法以及两种基线方法在一个与训练数据集不同的验证数据集上的泛化能力、准确性和效率。
1) 基线设置:
我们使用官方发布的 GeoTransformer [41] 和 SG-PGM [17] 版本。
我们使用 ScanNet-Mapping 数据对它们进行训练,并在 3RScan-Mapping 数据上进行评估,以测试它们在不同数据域中的泛化能力。
我们对 SG-PGM 的实现进行了与第七章节B部分类似的修改。
我们保持所有 3D 骨干网络的参数(如体素大小和点特征维度)一致。
同时,我们关闭所有方法的 ICP [72] 精修步骤以确保公平比较。
2) 配准精度:
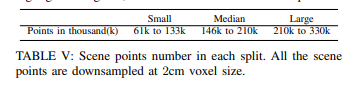
我们将来自 3RScan-Mapping 的 100 对场景分为三组:
76 对小场景对、13 对中等场景对和 11 对大场景对。
分组依据是每对场景中最大的点数。
我们总结了每个分组的场景点数范围,如表 V 所示。
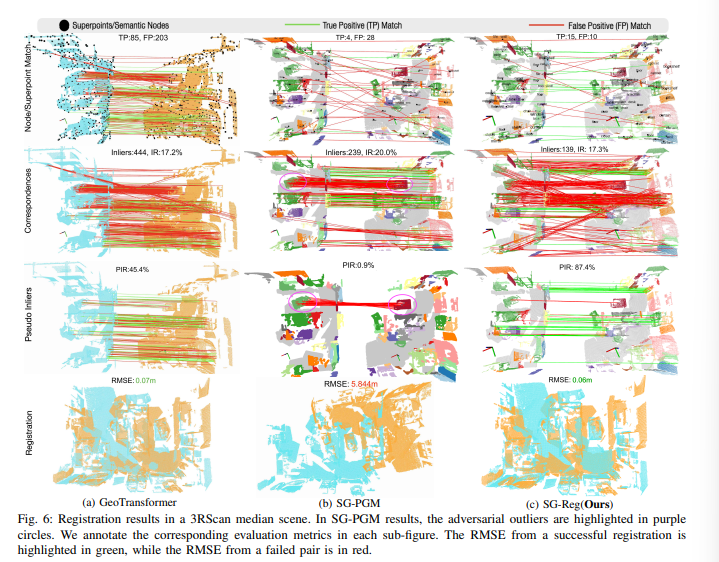
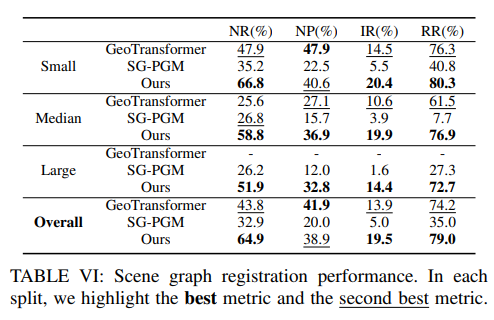
然而,在SG-PGM中,对抗性异常点的存在导致了配准失败。
如图6所示,这些异常点在几何上具有一致性,因此更难被剔除。
尽管进行了异常值剪枝,这些对抗性异常点仍然存在于伪内点中。
虽然对抗性异常点在GeoTransformer和我们的结果中也存在,但SG-PGM尤其容易受到影响,因为其高异常值比率导致无法有效剔除它们。
此外,SG-PGM的异常值剪枝方法依赖于批量加权SVD[44],这可能限制了其消除对抗性异常点的能力。
该方法搜索包含最多伪内点的小批量对应关系。
因此,这个包含对抗性异常点的小批量很可能获得最高的置信度得分,从而导致错误的SVD预测结果。
D. ScanNet 基准测试
一、论文核心思想(用一句话概括)
SG-Reg 的核心思想是:将三维点云配准问题转化为一个场景图匹配问题,通过联合提取并匹配点云中局部区域的几何形状特征和全局拓扑结构特征**,实现高效且泛化能力强的点云配准。二、传统方法的局限与 SG-Reg 的解决方案
- 传统局限:
- 基于点或局部特征的方法(如 FCGF, D3Feat):主要依赖局部几何描述符。在场景重叠度低、噪声大或存在重复结构时,这些局部特征容易产生歧义,导致匹配失败。
- 基于全局描述符的方法:缺乏局部细节,难以进行精确的位姿估计。
- SG-Reg 的解决方案:
- 构建场景图:将输入的点云分割成一组超点(superpoints),每个超点代表一个语义上一致的小区域(如一个桌腿、一个椅子座面)。将这些超点作为图中的节点。
- 建立边关系:如果两个超点区域在空间上是相邻的,就在它们之间建立一条边。这样,整个点云就构成了一个图结构(Scene Graph)。
- 将配准转化为图匹配:点云配准的任务就变成了为两个点云构成的场景图寻找节点之间的对应关系。找到正确的节点匹配后,就可以利用这些匹配的超点来估算点云之间的变换矩阵(旋转和平移)。
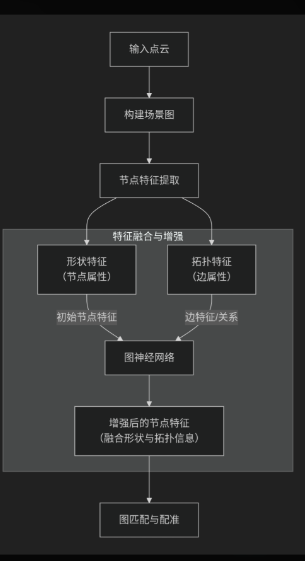
1. 形状特征 - 描述节点自身的几何属性
形状特征旨在描述每个超点(节点)所代表的局部区域的几何形状。它不依赖于其与其他节点的关系,是节点的“内在”属性。- 输入:一个超点
Pi所包含的所有原始点云坐标。 - 提取方法:
- Voxelization & 3D CNN:首先,将超点
Pi对应的不规则点云体素化,转换为一个规则的 3D 体素网格。 - 3D Sparse Convolution:然后,使用一个轻量级的 3D 稀疏卷积神经网络来处理这个体素网格。稀疏卷积能高效处理大部分为空的体素,节省计算资源。
- 特征池化:网络最终输出一个高维的特征向量,这个向量就是该超点的形状特征。这个特征对旋转和平移是敏感的,因为它编码了局部几何在特定坐标系下的信息。
- Voxelization & 3D CNN:首先,将超点
- 作用:形状特征提供了强大的局部区分能力。例如,一个圆柱形的桌腿和一个平坦的桌面,它们的形状特征会有显著差异。
2. 拓扑特征 - 描述节点间的结构关系
-
-
2. 拓扑特征 - 描述节点间的结构关系
拓扑特征是 SG-Reg 的创新核心。它描述了节点在整个图结构中的“位置”和“连接关系”,是节点的“关系”属性。这种特征对刚体变换(旋转、平移)具有不变性。- 核心思想:不关心一个桌腿“绝对”长什么样(形状特征),而关心它“相对于”桌面和其他桌腿的位置和连接关系。即使点云被旋转了,这种相对关系也是不变的。
- 提取方法:
- 边的属性:对于图中连接节点
i和节点j的边,定义其属性(拓扑描述符)为:e_ij = [d_ij, θ_ij, φ_ij]d_ij:两个超点中心之间的欧氏距离。θ_ij,φ_ij:表示从节点i到j的方向向量(类似于球坐标中的角度)。这些值在点云整体旋转和平移后保持不变。
- 利用图神经网络聚合拓扑信息:
- 初始节点特征:每个节点用其形状特征进行初始化。
- 消息传递:图神经网络通过多层消息传递机制,让节点之间交换信息。在每一层,一个节点会聚合其邻居节点的信息。
- 聚合方式:在聚合邻居
j的信息时,会使用它们之间的边特征e_ij作为权重或条件。因此,节点i最终学到的特征,不仅包含了自身的形状信息,还编码了它与周围节点的空间关系(即拓扑结构)。 - 输出:经过几层 GNN 处理后,每个节点都会得到一个增强后的特征。这个特征是一个联合表示,同时融合了节点自身的局部几何形状和其在全局场景中的拓扑上下文。
- 边的属性:对于图中连接节点
四、优势总结:为什么这种方法更优?
- 泛化能力强:
- 拓扑不变性:拓扑特征对旋转平移不变,使得模型在训练集上未见过的场景布局和位姿下也能表现良好。
- 形状+拓扑互补:即使局部形状因为视角、遮挡而变得不完整或相似,全局拓扑结构也能提供强有力的约束来消除歧义。反之亦然。
- 高效:
- 图的规模(节点数量)远小于原始点云的数量级。在图上进行匹配比在成千上万个点之间匹配要快得多。
- 场景图自然地抽象了场景,减少了冗余计算。
- 鲁棒性强:
- 对低重叠率场景特别有效。因为拓扑关系是全局的,即使两个点云只有一小部分重叠,只要这部分的局部结构和它们之间的相对关系是独特的,就能被正确匹配。
-



 浙公网安备 33010602011771号
浙公网安备 33010602011771号