openvslam 三角化

https://blog.csdn.net/weixin_43013761/article/details/124328735

 

 

 

1. 提取ORB特征点

#include <opencv2/opencv.hpp>
#include <opencv2/features2d.hpp>
#include <opencv2/core.hpp>

cv::Ptr<cv::ORB> orb = cv::ORB::create();
std::vector<cv::KeyPoint> keypoints1, keypoints2;
cv::Mat descriptors1, descriptors2;

// 提取特征点
orb->detectAndCompute(image1, cv::noArray(), keypoints1, descriptors1);
orb->detectAndCompute(image2, cv::noArray(), keypoints2, descriptors2);

2. 匹配特征点

cv::BFMatcher matcher(cv::NORM_HAMMING, true);
std::vector<cv::DMatch> matches;
matcher.match(descriptors1, descriptors2, matches);

3. 提取匹配的点　　

std::vector<cv::Point2f> points1, points2;
for (const auto& match : matches) {
    points1.push_back(keypoints1[match.queryIdx].pt);
    points2.push_back(keypoints2[match.trainIdx].pt);
}

　

4. 三角化

假设你有两个相机位姿 T1 和 T2，它们是4x4的变换矩阵。

　

cv::Mat T1 = ...; // 世界到相机1的变换矩阵
cv::Mat T2 = ...; // 世界到相机2的变换矩阵

std::vector<cv::Point3f> points3D;
for (size_t i = 0; i < points1.size(); i++) {
    cv::Mat A(4, 4, CV_64F);
    ... A的具体

    // 使用SVD分解
    cv::Mat u, w, vt;
    cv::SVD::compute(A, w, u, vt);

    // 3D点
    cv::Mat X = vt.row(3).t() / vt.row(3).at<double>(3);
    points3D.emplace_back(X.at<double>(0), X.at<double>(1), X.at<double>(2));
}

　　

opnevslam 对应

Vec3_t triangulator::triangulate(const cv::Point2d& pt_1, const cv::Point2d& pt_2, const Mat34_t& P_1, const Mat34_t& P_2) {
    Mat44_t A;

    A.row(0) = pt_1.x * P_1.row(2) - P_1.row(0);
    A.row(1) = pt_1.y * P_1.row(2) - P_1.row(1);
    A.row(2) = pt_2.x * P_2.row(2) - P_2.row(0);
    A.row(3) = pt_2.y * P_2.row(2) - P_2.row(1);

    const Eigen::JacobiSVD<Mat44_t> svd(A, Eigen::ComputeFullU | Eigen::ComputeFullV);

    const Vec4_t v = svd.matrixV().col(3);
    return v.block<3, 1>(0, 0) / v(3);
}

　　5. 输出3D点

　　

for (const auto& point : points3D) {
    std::cout << "3D Point: " << point << std::endl;
}

　　

 

 

 

 

 

 

 

 利用叉乘的性质

 

 

 

 

 

 

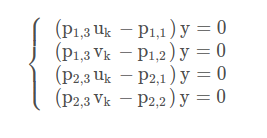
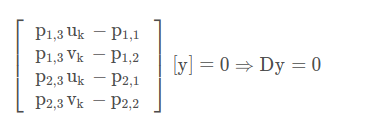
 为什么要这么算？

1加快速度

 

2噪声干扰

 

 

 

 

https://blog.csdn.net/michaelhan3/article/details/89483148

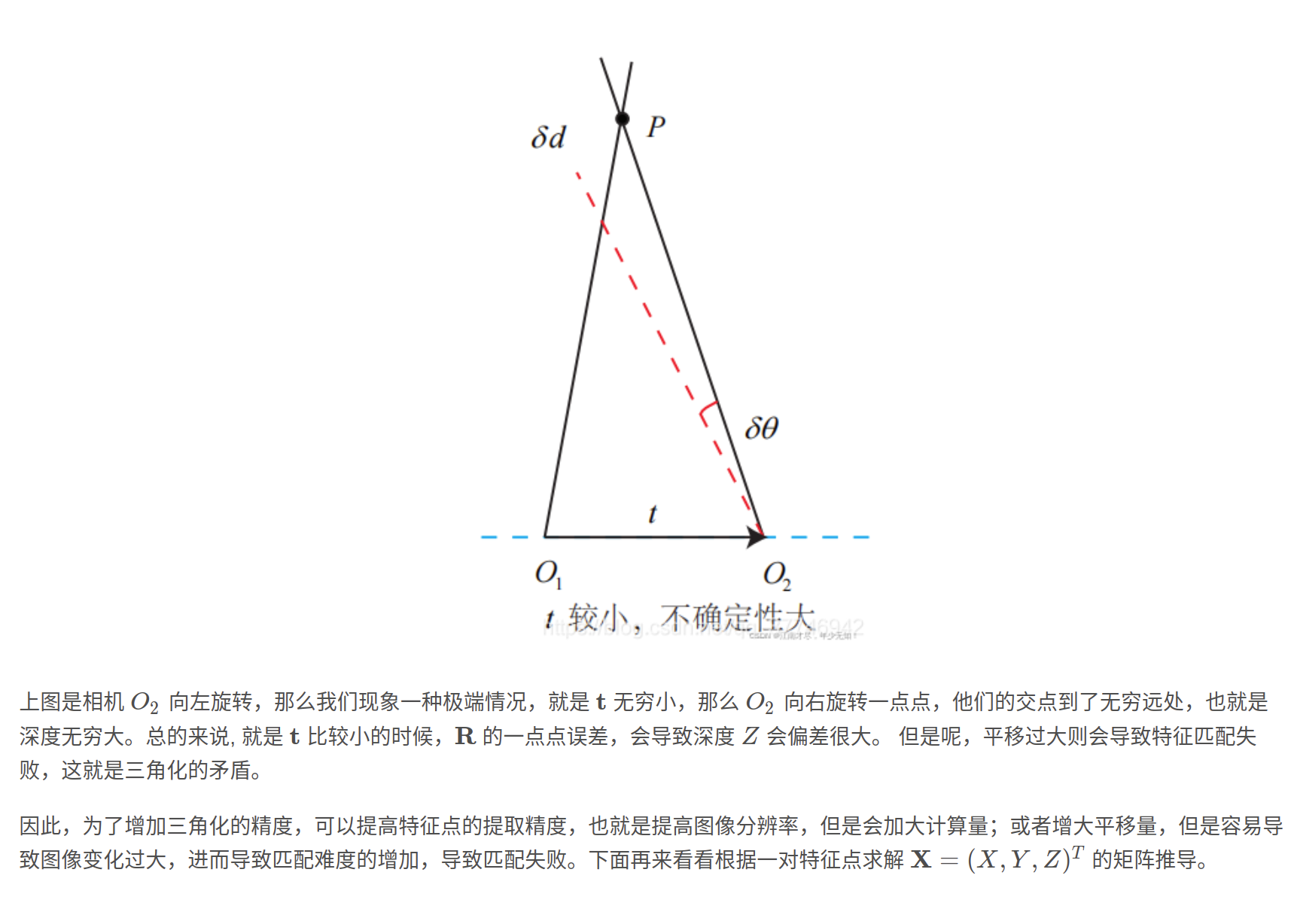
一 ：三角化的提出

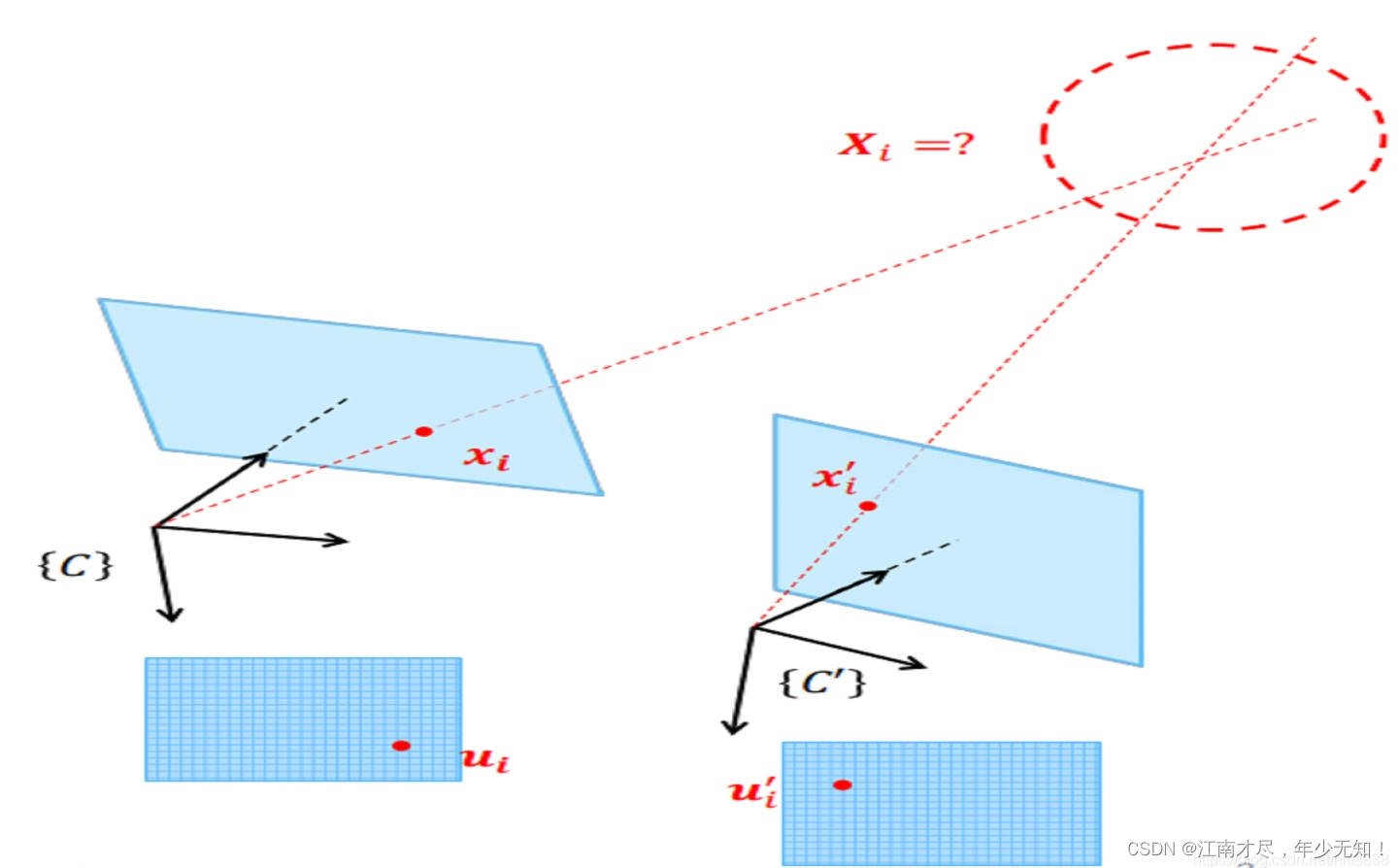
三角化最早由高斯提出，并应用于测量学中。简单来讲就是：在不同的位置观测同一个三维点P(x, y, z)，已知在不同位置处观察到的三维点的二维投影点X1(x1, y1), X2(x2, y2)，利用三角关系，恢复出三维点的深度信息z。

 

一 ：三角化的提出

三角化最早由高斯提出，并应用于测量学中。简单来讲就是：在不同的位置观测同一个三维点P(x, y, z)，已知在不同位置处观察到的三维点的二维投影点X1(x1, y1), X2(x2, y2)，利用三角关系，恢复出三维点的深度信息z。

 

二： 三角化求解

(1) 利用叉乘进行消元进行求解

s1x1 = s2Rx2 + t 公式(1)

左右两边同时乘以x1的反对称矩阵，可得：

s1x1^x1 = 0 = s2x1^Rx2 + x1^t 公式(2)

由上式可解得s2，

将s2代入公式(1)，可求得s1

该方法也是视觉slam十四讲那本书里讲解三角化里提到的方法。

二： 三角化求解

(1) 利用叉乘进行消元进行求解

s1x1 = s2Rx2 + t 公式(1)

左右两边同时乘以x1的反对称矩阵，可得：

s1x1^x1 = 0 = s2x1^Rx2 + x1^t 公式(2)

由上式可解得s2，

将s2代入公式(1)，可求得s1

该方法也是视觉slam十四讲那本书里讲解三角化里提到的方法。

 

(2) 线性三角化法

 

 

 

 

 

 

 openvslam代码

Vec3_t triangulator::triangulate(const cv::Point2d& pt_1, const cv::Point2d& pt_2, const Mat34_t& P_1, const Mat34_t& P_2) 
{
    //H矩阵
    Mat44_t A;
    //H矩阵每一行赋值
    A.row(0) = pt_1.x * P_1.row(2) - P_1.row(0);//u1p1(3)-p1(1)
    A.row(1) = pt_1.y * P_1.row(2) - P_1.row(1);//v1p1(3)-p1(2)
    A.row(2) = pt_2.x * P_2.row(2) - P_2.row(0);//u2p2(3)-p2(1)
    A.row(3) = pt_2.y * P_2.row(2) - P_2.row(1);//v2p2(3)-p2(2)
	//SVD求解，齐次坐标X为H的最小奇异值的奇异向量
    const Eigen::JacobiSVD<Mat44_t> svd(A, Eigen::ComputeFullU | Eigen::ComputeFullV);
	//因为SVD解可能不满足齐次坐标形式（第四个元素为0），所以需要进行归一化处理
    const Vec4_t v = svd.matrixV().col(3);
    return v.block<3, 1>(0, 0) / v(3);//归一化  block：从下标(0,0)开始，取3*1区域
}

　　

VINS-Mono中相关代码

void FeatureManager::triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,
                        Eigen::Vector2d &point0, Eigen::Vector2d &point1, Eigen::Vector3d &point_3d)
{
    Eigen::Matrix4d design_matrix = Eigen::Matrix4d::Zero();
    design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
    design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
    design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
    design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
    Eigen::Vector4d triangulated_point;
    triangulated_point =
              design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
    point_3d(0) = triangulated_point(0) / triangulated_point(3);
    point_3d(1) = triangulated_point(1) / triangulated_point(3);
    point_3d(2) = triangulated_point(2) / triangulated_point(3);
}

　　

ORB-SLAM21中的三角形法的代码如下：

void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{
    cv::Mat A(4,4,CV_32F);
 
    A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
    A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
    A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
    A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);
 
    cv::Mat u,w,vt;
    cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
    x3D = vt.row(3).t();
    x3D = x3D.rowRange(0,3)/x3D.at<float>(3);
}

(3) 解二元一次方程

视觉slam十四讲单目重建深度滤波部分代码。利用Cramer's法则，
按照对极几何中的定义，设x1, x2为两个特征点的归一化坐标，则它们满足：

s1x1 = s2Rx2 + t 公式(1)

=> s1x1 - s2Rx2 = t 公式(2)

对公式(2)左右两侧分别乘以x1T，得：

s1x1Tx1 - s2x1TRx2 = x1T t 公式(3)

对公式(2)左右两侧分别乘以(Rx2)T，得：

s1(Rx2)Tx1 - s2(Rx2)TRx2 = (Rx2)T t 公式(4)

由公式(3)和公式(4)可以联立，然后可以利用Cramer's法则（参见线性代数书）进行求解。

 

 

　　

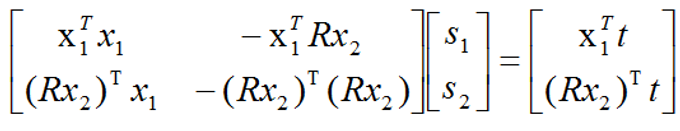
• 在SVO2中的实现如下

• 

   

 

bool depthFromTriangulation(
    const SE3& T_search_ref,
    const Vector3d& f_ref,
    const Vector3d& f_cur,
    double& depth)
{
  Matrix<double,3,2> A; A << T_search_ref.rotation_matrix() * f_ref, f_cur;
  const Matrix2d AtA = A.transpose()*A;
  if(AtA.determinant() < 0.000001)
    return false;
  // d = - (ATA)^(-1) * AT * t
  const Vector2d depth2 = - AtA.inverse()*A.transpose()*T_search_ref.translation();
  depth = fabs(depth2[0]);
  return true;
}