视觉VO（3）三角化 （图像匹配点和位姿RT已知求解深度进而求解三维点云）

 2D-2D可以从两个单目图像中估计一个Rt，t是没有真实尺度的，接下来进一步三角化求解三维坐标和深度，

原理理解

https://www.bilibili.com/video/BV1ie4y1f7XG/?spm_id_from=333.788&vd_source=f88ed35500cb30c7be9bbe418a5998ca

 

 

具体计算计算

https://blog.csdn.net/KYJL888/article/details/107222533

三角测量的目的是用来确定图片中某一个点的深度。为什么会有这样的需求呢？我们在前面的博客中提到了对极几何与单应变换。

在前面其实已经提到过了，在单目VO中，虽然我们可以通过本质矩阵与单应矩阵恢复出相机变换的位姿，但是这两种方法确定的位姿变换是具有尺度不确定性的。在双目vo中，我们会首先使用三角测量恢复出深度信息，再进行位姿估计。

 

 

1原理

其他测距方法

1. 主动方法
   • 结构光: 光已知空间方向的投影光线的集合称为结构光，结构光激光散斑通过投射具有高度伪随机性的激光散斑，会随着不同距离变换不同的图案，对三维空间直接标记，通过观察物体表面的散斑图案就可以判断其深度。
   • ToF: 飞行时间法，通过连续发射光脉冲（一般是不可见光），到被观测物体上，然后接收从物体反射回去的光脉冲，通过探测光脉冲的往返飞行时间来计算被测物体距离。
   • LIDAR: 激光雷达
2. 使用深度学习构建神经网络对图像深度进行预测

单目测距

第一种思路

第一帧为基础

世界为基础

 

 

 

 

 

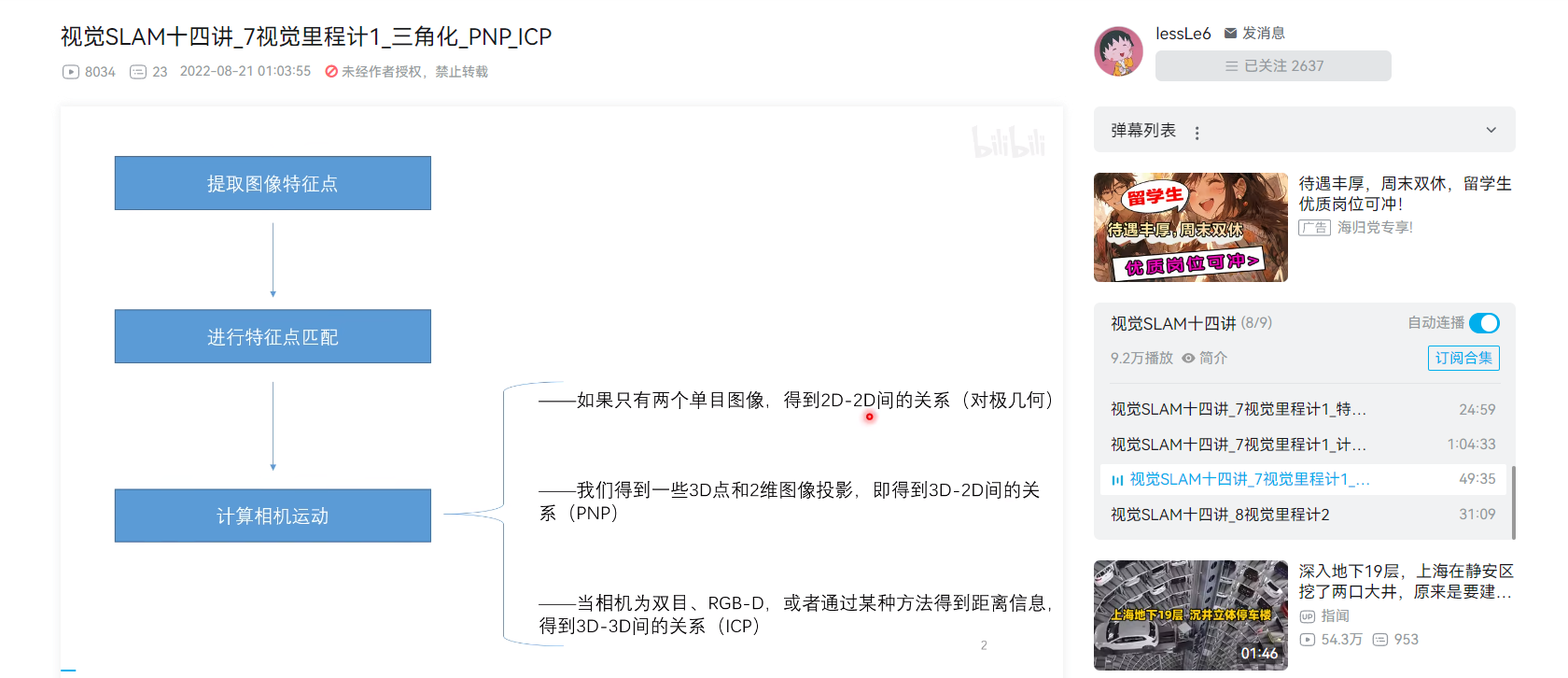
通过对极约束知道了  ，想要求解的是两个特征点的深度  。当然这两个深度是可以分开求的，如，先求  ，那么对上式左乘一个  ，得：

该式左侧为零，右侧可看成  的一个方程，可以根据它直接求得  。有了  ，  也非常容易求出。于是，得到了两帧下的点的深度，确定了它们的空间坐标。由于噪声的存在，估得的  不一定精确使上式为零，所以常见的做法是求最小二乘解而不是零解。

 

代码实现（自己实现）

首先是上述思路的解法

bool depthFromTriangulation(
        const SE3& T_search_ref,
        const Vector3d& f_ref,
        const Vector3d& f_cur,
        double& depth)
{
    Matrix<double,3,2> A;
    A << T_search_ref.rotation_matrix()*f_ref, f_cur;
    const Matrix2d AtA = A.transpose()*A;
    if(AtA.determinant() < 0.000001)
        return false;
    const Vector2d depth2 = - AtA.inverse()*A.transpose()*T_search_ref.translation();
    depth = fabs(depth2[0]);
    return true;
}

　　

第二种思路

 自己实现的代码

　　

// 用三角化计算深度
    SE3 T_R_C = T_C_R.inverse();//T_C_R reference to current transformation matrix
    Vector3d f_ref = px2cam( pt_ref );//参考帧的像素坐标转换到相机坐标系的坐标
    f_ref.normalize();//参考帧上的点在相机坐标系下的归一化的坐标x_1
    Vector3d f_curr = px2cam( pt_curr );//当前帧的像素坐标转换到相机坐标系的坐标
    f_curr.normalize();//当前帧上的点在相机坐标系下的归一化的坐标x_2
    
    // 方程
    // d_ref * f_ref = d_cur * ( R_RC * f_cur ) + t_RC//d_ref=x_1,对应s_1x_1=s_2(R*x_2)+t
    // => [ f_ref^T f_ref, -f_ref^T f_cur ] [d_ref] = [f_ref^T t]//s_1x_1^Tx_1=s_2x_1^Tx_2+x_1^Tt
    //    [ f_cur^T f_ref, -f_cur^T f_cur ] [d_cur] = [f_cur^T t]//s_2x_2^Tx_1=s_2x_2^Tx_2+x_2^Tt
    // 二阶方程用克莱默法则求解并解之
    Vector3d t = T_R_C.translation();//平移向量t
    Vector3d f2 = T_R_C.rotation_matrix() * f_curr; //Rx_2
    Vector2d b = Vector2d ( t.dot ( f_ref ), t.dot ( f2 ) );//tx_1,tRx_2
    double A[4];
    A[0] = f_ref.dot ( f_ref );//x_1*x_1
    A[2] = f_ref.dot ( f2 );//x_1Rx_2
    A[1] = -A[2];//-x_1Rx_2
    A[3] = - f2.dot ( f2 );//-x_1Rx_2*x_1Rx_2
    double d = A[0]*A[3]-A[1]*A[2];//
    Vector2d lambdavec = 
        Vector2d (  A[3] * b ( 0,0 ) - A[1] * b ( 1,0 ),
                    -A[2] * b ( 0,0 ) + A[0] * b ( 1,0 )) /d;
    Vector3d xm = lambdavec ( 0,0 ) * f_ref;
    Vector3d xn = t + lambdavec ( 1,0 ) * f2;
    Vector3d d_esti = ( xm+xn ) / 2.0;  // 三角化算得的深度向量
    double depth_estimation = d_esti.norm();   // 深度值
    
运用克莱姆法则可以很有效地解决以下方程组。

　　

代码实现（使用opencv提供的接口）

void triangulation ( 
    const vector< KeyPoint >& keypoint_1, 
    const vector< KeyPoint >& keypoint_2, 
    const std::vector< DMatch >& matches,
    const Mat& R, const Mat& t, 
    vector< Point3d >& points )
{
    //相机第一个位置处的位姿
    Mat T1 = (Mat_<float> (3,4) <<
        1,0,0,0,
        0,1,0,0,
        0,0,1,0);
    //相机第二个位置处的位姿
    Mat T2 = (Mat_<float> (3,4) <<
        R.at<double>(0,0), R.at<double>(0,1), R.at<double>(0,2), t.at<double>(0,0),
        R.at<double>(1,0), R.at<double>(1,1), R.at<double>(1,2), t.at<double>(1,0),
        R.at<double>(2,0), R.at<double>(2,1), R.at<double>(2,2), t.at<double>(2,0)
    );
    
    // 相机内参
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    vector<Point2f> pts_1, pts_2;
    for ( DMatch m:matches )
    {
        // 将像素坐标转换至相机平面坐标，为什么要这一步，上面推导中有讲
        pts_1.push_back ( pixel2cam( keypoint_1[m.queryIdx].pt, K) );
        pts_2.push_back ( pixel2cam( keypoint_2[m.trainIdx].pt, K) );
    }
    
    Mat pts_4d;
    //opencv提供的三角测量函数
    cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );
    
    // 转换成非齐次坐标
    for ( int i=0; i<pts_4d.cols; i++ )
    {
        Mat x = pts_4d.col(i);
        x /= x.at<float>(3,0); // 归一化
        Point3d p (
            x.at<float>(0,0), 
            x.at<float>(1,0), 
            x.at<float>(2,0) 
        );
        points.push_back( p );
    }
}
 
Point2f pixel2cam ( const Point2d& p, const Mat& K )
{
    return Point2f
    (
        ( p.x - K.at<double>(0,2) ) / K.at<double>(0,0), 
        ( p.y - K.at<double>(1,2) ) / K.at<double>(1,1) 
    );
}

　　最后归一化解释

 x /= x.at<float>(3,0); // 归一化

再齐次坐标下点是1*4[x,y,z,1]的并非1*3【x,y,z】，经过计算x[3]=p[3]未必刚好为1，所以都除以p[3]归一化。

反正齐次坐标整体乘上和除以某个系数都是一样的。

 

 

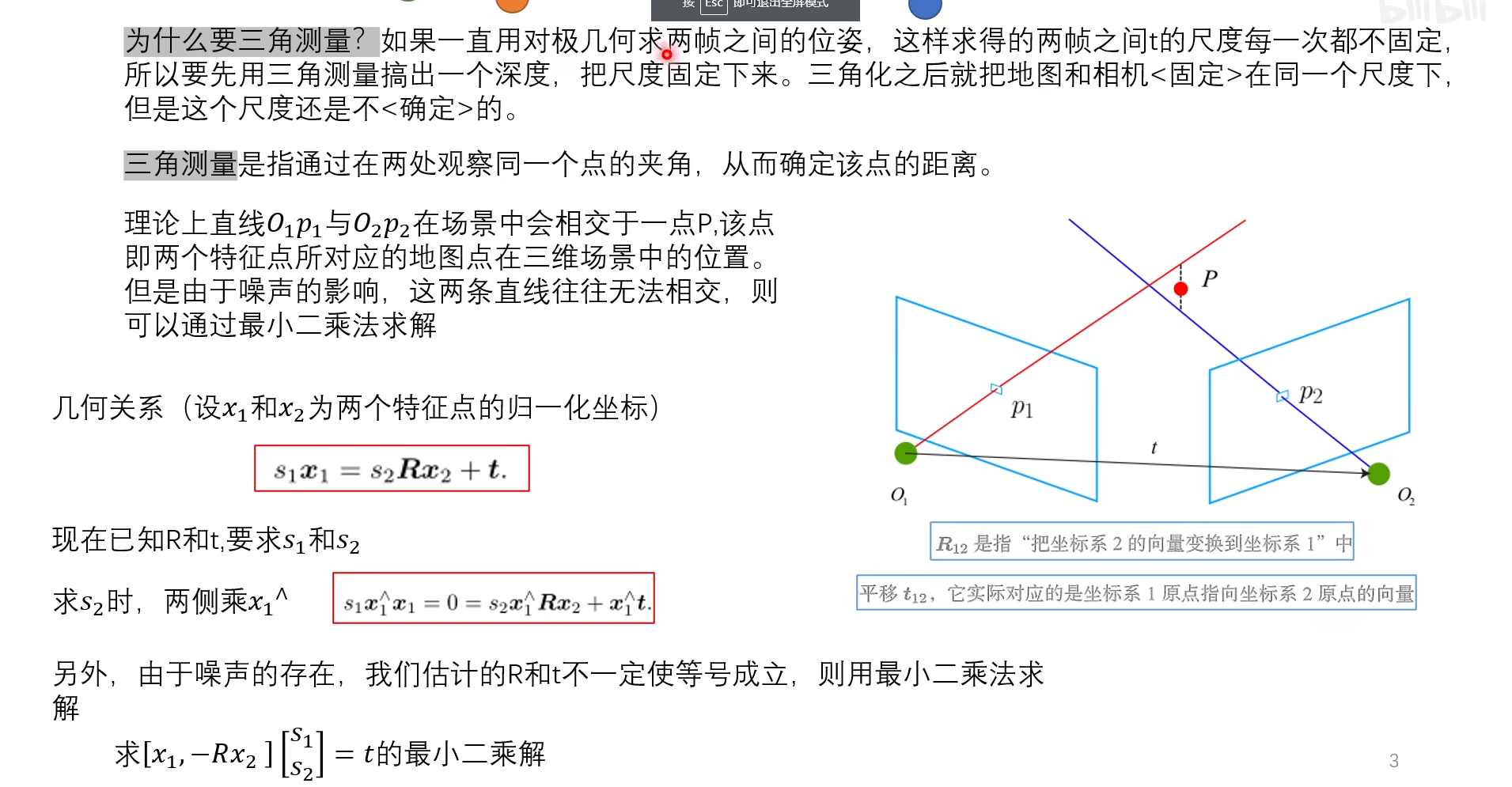
第三种思路（最小二乘法求解深度）

 

 

 由于 xk=[uk vk 1] 所以第三行是1 ，可以用来单独提取深度表达式

然后再带入第一和第二行替换表达，从而为构建等式

 

 

最小二乘求解

 

// vins中初始化sfm时根据一个三维点在两帧中的投影位置确定三维点位置
void GlobalSFM::triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,
						Vector2d &point0, Vector2d &point1, Vector3d &point_3d)
{
	Matrix4d design_matrix = Matrix4d::Zero();
	design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
	design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
	design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
	design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
	Vector4d triangulated_point;
	triangulated_point =
		      design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
	point_3d(0) = triangulated_point(0) / triangulated_point(3);
	point_3d(1) = triangulated_point(1) / triangulated_point(3);
	point_3d(2) = triangulated_point(2) / triangulated_point(3);
}

4 orb -slam形式

Triangulate(kp1,kp2,P1,P2,p3dC1);

 

 https://wym.netlify.app/2019-06-17-orb-slam2-monocular-initialization/

2.6 三角化 3D 点

 

 

 

 

 void Initializer::Triangulate(
    const cv::KeyPoint &kp1,    // 特征点, in reference frame
    const cv::KeyPoint &kp2,    // 特征点, in current frame
    const cv::Mat &P1,          // 投影矩阵P1
    const cv::Mat &P2,          // 投影矩阵P2
    cv::Mat &x3D)               // 三维点
    {
        cv::Mat A(4,4,CV_32F);

        //构造参数矩阵A
        A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
        A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
        A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
        A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);

        //奇异值分解的结果
        cv::Mat u,w,vt;

        //对系数矩阵A进行奇异值分解
        cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
        //根据前面的结论，奇异值分解右矩阵的最后一行其实就是解，原理类似于前面的求最小二乘解，四个未知数四个方程正好正定
        //别忘了我们更习惯用列向量来表示一个点的空间坐标
        x3D = vt.row(3).t();
        //为了符合齐次坐标的形式，使最后一维为1
        x3D = x3D.rowRange(0,3)/x3D.at<float>(3);
    }

　　

误差分析

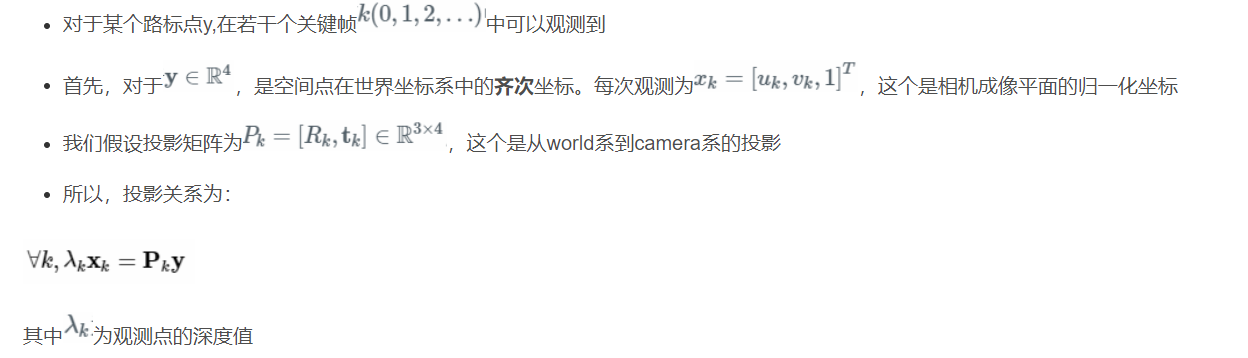
1 基线影响因素

三角平移是由平移得到的，有平移才会有对极几何约束的三角形。因此，纯旋转是无法使用三角测量的，对极约束将永远满足。在平移时，三角测量有不确定性，会引出三角测量的矛盾。

基线越小误差越大

基线越大导致匹配越差，进而导致效果越差。

在保证匹配的前提下，基线越大越好

2计算影响因素

用概率方法更新矫正深度值

从上述讲述中，我们已经知道通过两帧图像的匹配点，可以得到一个等式，可以计算出这一点的深度值，所以，如果有n副图像进行匹配，那我们会得到n-1个等式。

此时我们就可以计算出这一点的n-1个空间位置的测量值。

（有必要全部参与么？一定都是好的么？如何Ransac剔除不好的点）

好的测量值是符合正态分布的，噪声符合均匀分布，此时我们可以通过一些概率的方法对多次测量结果进行融合，得到更鲁棒的结果。

• 在SVO中，使用贝叶斯方法(最大后验概率)进行更新

• 在LSD中，使用卡尔曼滤波进行深度测量值的滤波

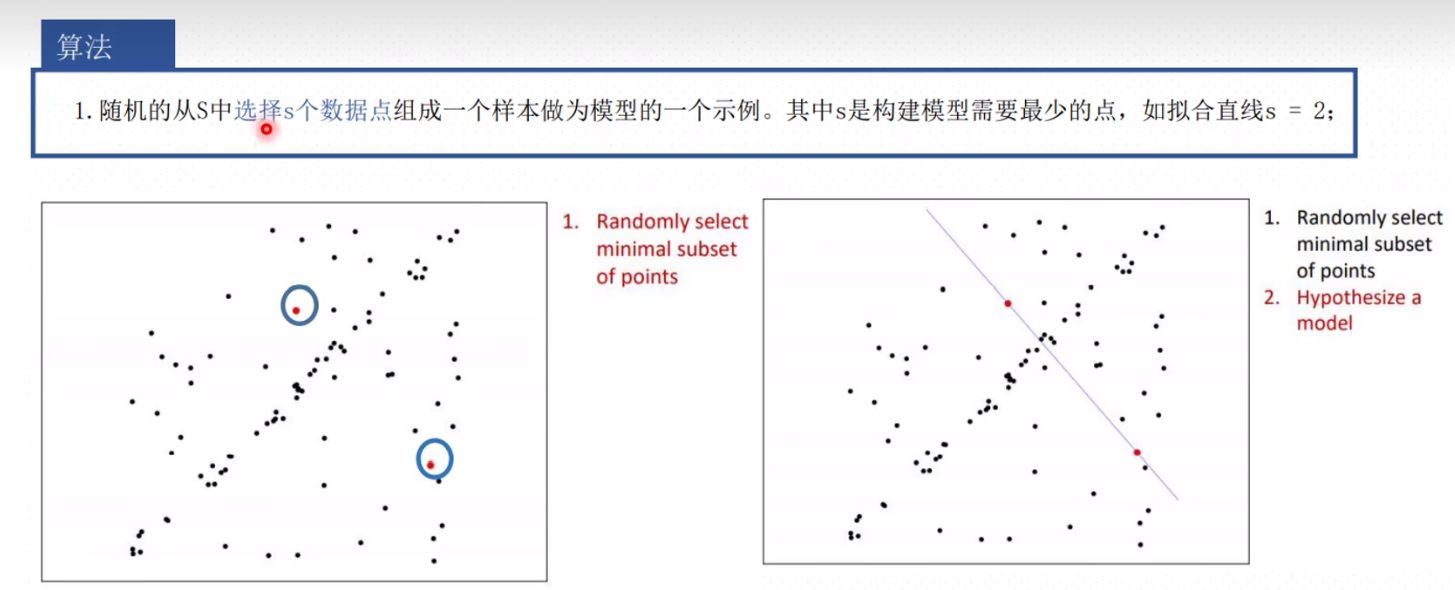
Ransac 求解

默认了所有的观测帧都参与了优化，但是可以使用Ransac来剔除不好点

对于两个视图，多对匹配点得情况，可以使用rasanc剔除外点，求解精确得解。

ransac三角测量得方法步骤是：

1. 随机挑选一对视角匹配点，
2. 计算三维空间点坐标，
3. 重投影到视图，计算重投影误差，误差较大得认为是外点。
4. 重复上面过程，挑选最佳内点，并计算点云。