综合（）单目相机三角化BA优化全流程

 

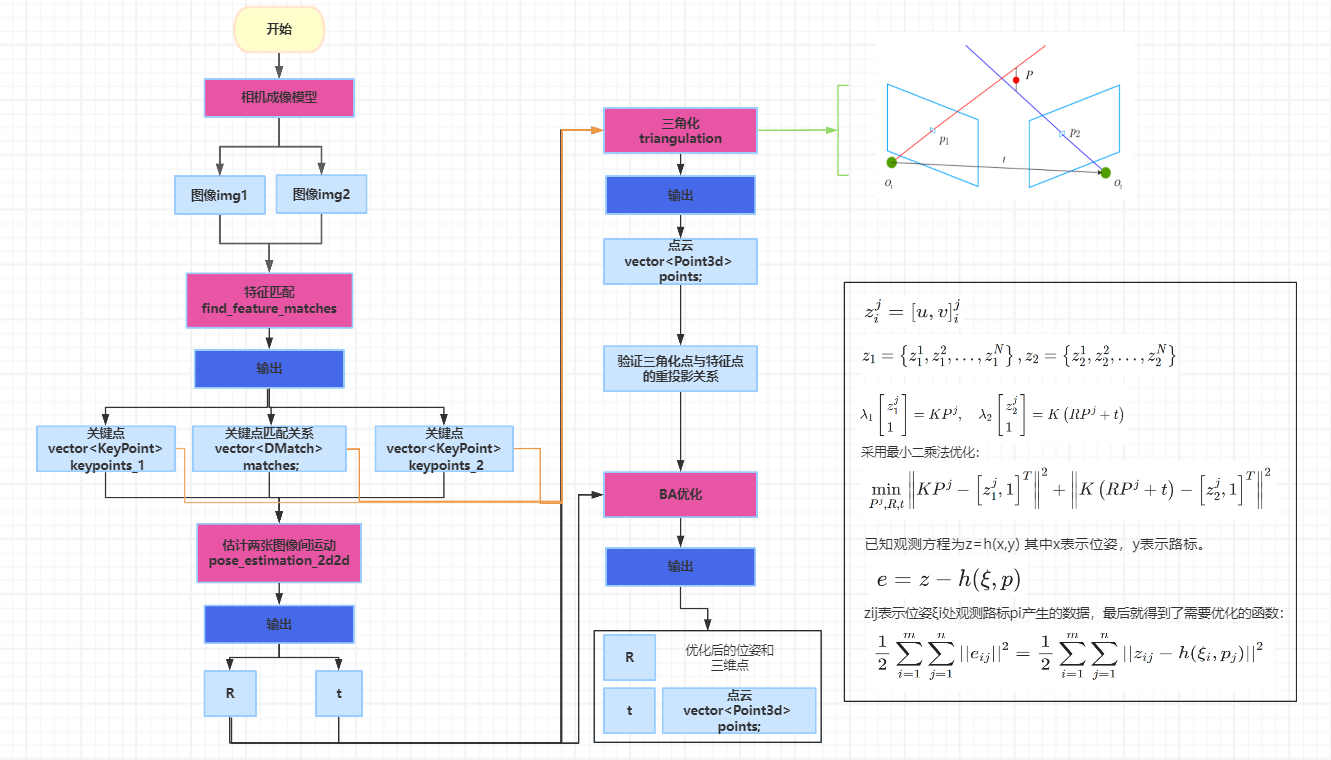
1相机成像模型

https://www.cnblogs.com/wangguchangqing/p/8126333.html

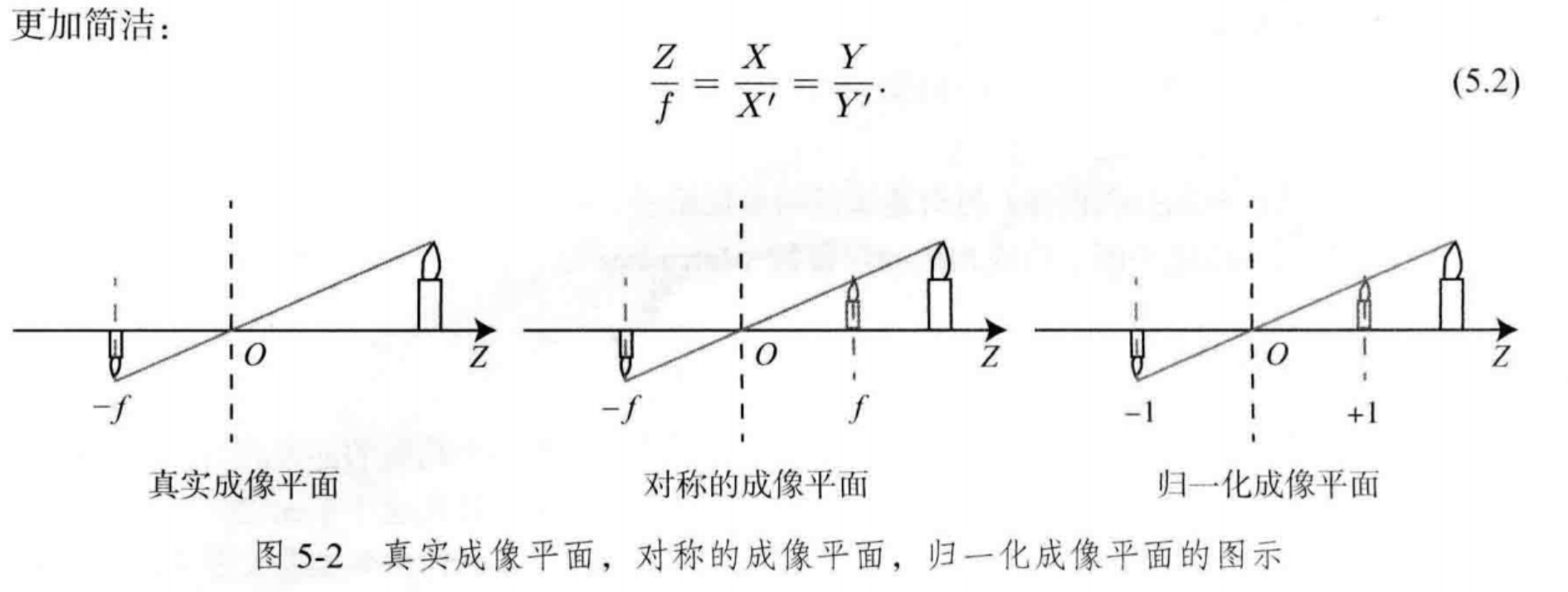
1-1 基本模型

 

 

 

 内参数矩阵（Camera Intrinsics）K，

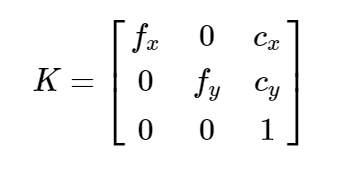
 <br />

 

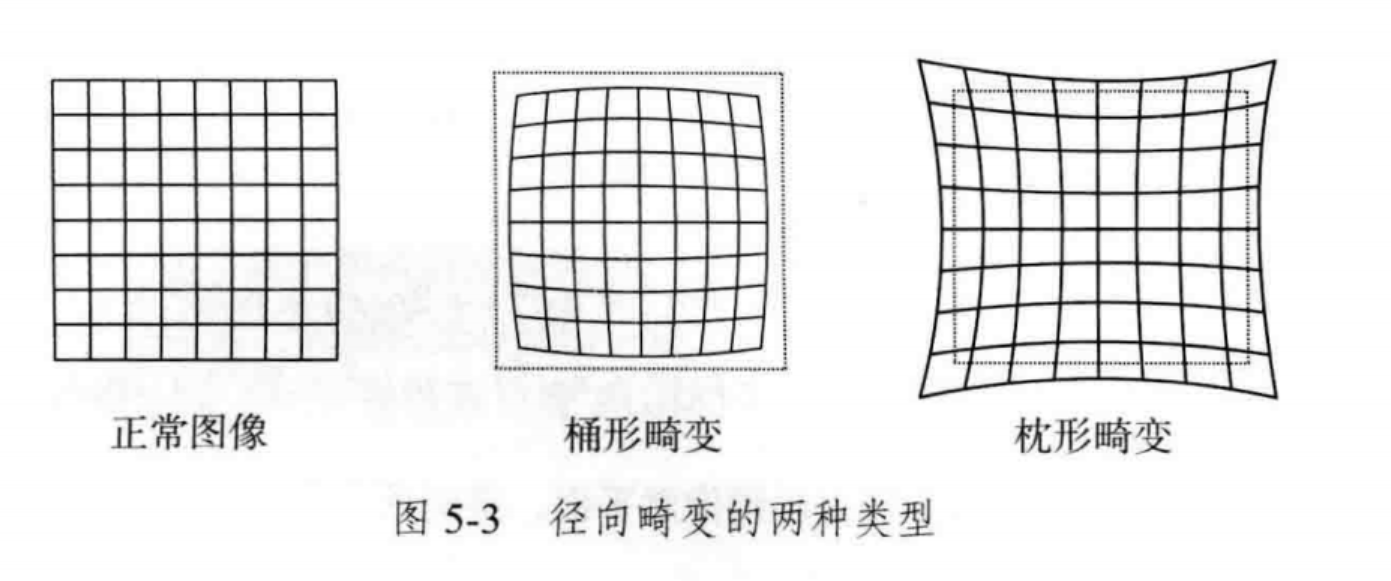
1-2 畸变矫正

 

 

 

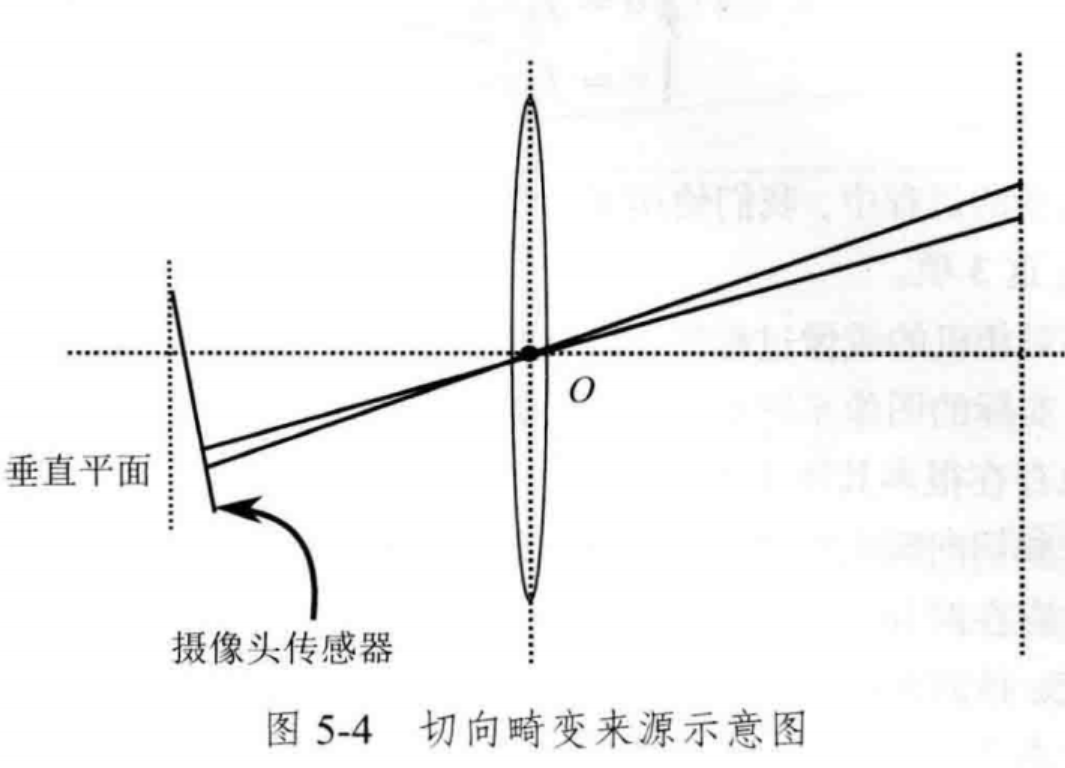
1-3外参

 

https://www.cnblogs.com/wangguchangqing/p/8126333.html

 

 

 

 

 

 

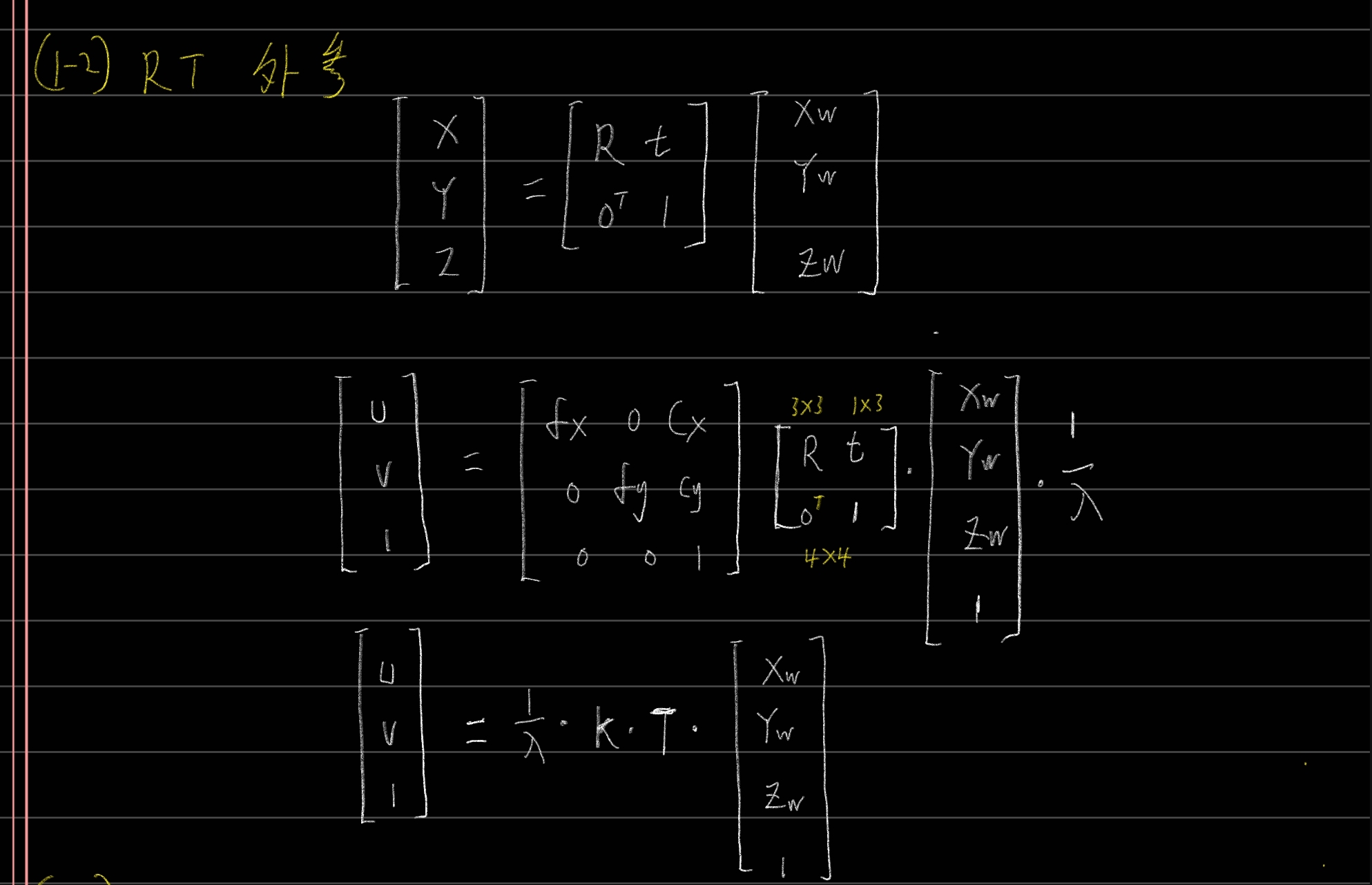
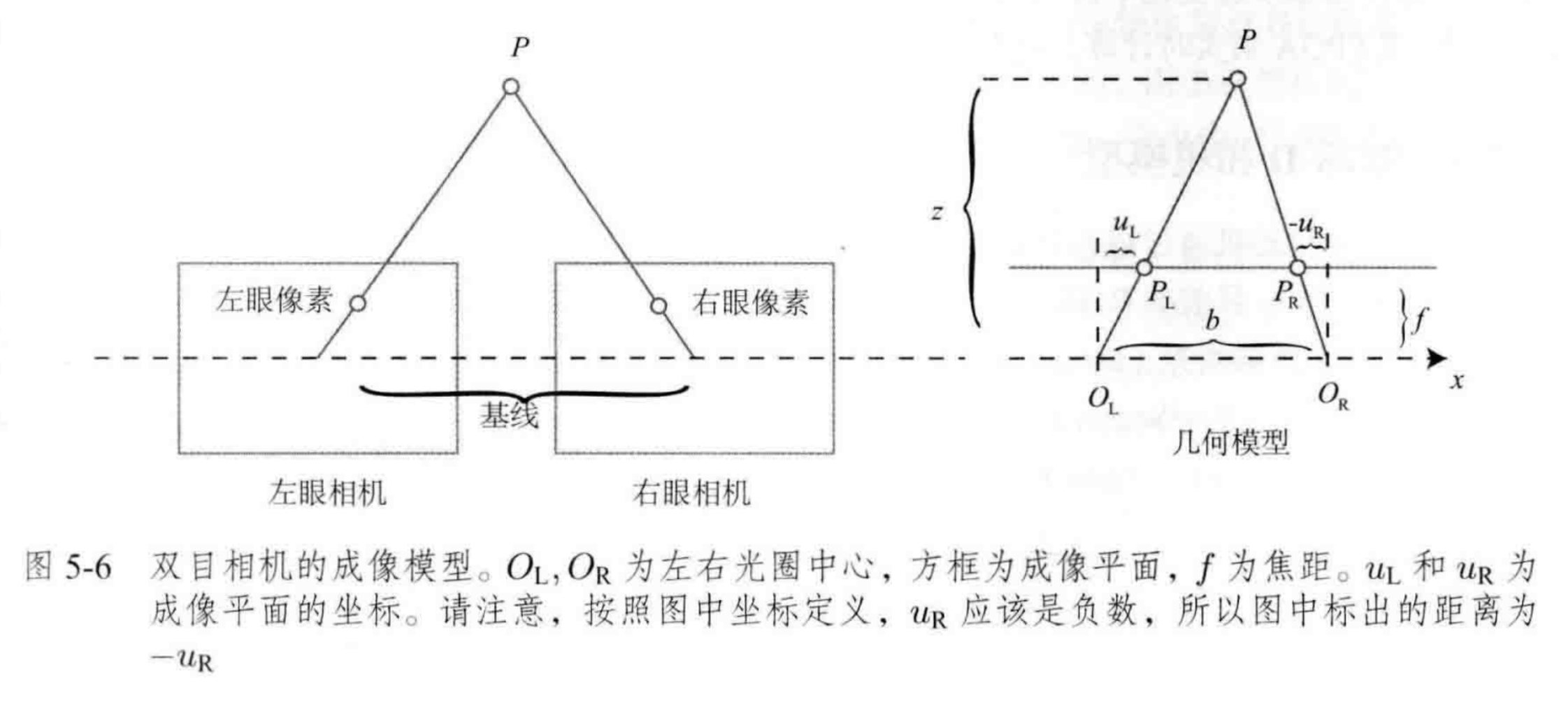
 1-4 双目模型

 

 

 

 

2 单目双图SVD分解求运动，E和F矩阵

 2D-2D

 

 

 

 

具体计算

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 三角化

 

 

 

2D-2D

3-1 原理

 

https://zhehangt.github.io/2017/03/06/SLAM/Basic/Triangularization/

 

 但由于误差的存在，上述方程通常不会严格成立，所以更常见的做法是求最小二乘解而不是零解。

 

最后根据

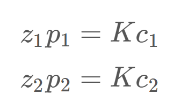
 求解出三维点坐标 c1    c2=R*c1+t

 

3-2实际计算 opecv算法

https://blog.csdn.net/KYJL888/article/details/107222533

https://scm_mos.gitlab.io/vision/triangulate/

 

 

如图所示，已知相机内参，外参以及匹配点，求解三维空间点的坐标。

原理分析

设：

第i个相机投影矩阵，以及其行向量。

 三维点的坐标：

 

 在第i个相机中的投影的图像坐标是：

根据投影方程得到：

这里省略了深度，默认归一化了.后期叉乘为0系数还是丢了

上式两侧同时叉乘<span id="MathJax-Span-93" class="mrow"><span id="MathJax-Span-94" class="msubsup"><span id="MathJax-Span-95" class="mi">x<span id="MathJax-Span-96" class="mi">i:

计算

 

 

 

 得到

 

 

第三个方程与前两个线性相关，因此

 1个观察点提供2个约束，X有三个自由度，至少2对点，也就是至少两个视角。

 对齐次方程<span id="MathJax-Span-258" class="mrow"><span id="MathJax-Span-259" class="msubsup"><span id="MathJax-Span-260" class="mi">A<span id="MathJax-Span-261" class="mi">T<span id="MathJax-Span-262" class="mi">A进行SVD分解，最小特征值对应得特征向量就是点得三维坐标。

对于多个视角观察，可以求得最小二乘解。

Ransac 求解

对于两个视图，多对匹配点得情况，可以使用rasanc剔除外点，求解精确得解。

ransac三角测量得方法步骤是：

1. 随机挑选一对视角匹配点，
2. 计算三维空间点坐标，
3. 重投影到视图，计算重投影误差，误差较大得认为是外点。
4. 重复上面过程，挑选最佳内点，并计算点云。

误差分析

三角平移是由平移得到的，有平移才会有对极几何约束的三角形。因此，纯旋转是无法使用三角测量的，对极约束将永远满足。在平移时，三角测量有不确定性，会引出三角测量的矛盾。

 

 对于三角测量，平移较小时误差较大，平移较大时误差越小，因此在构建三角测量时可以选择基线较大得视图。

3-3 完整代码

https://cloud.tencent.com/developer/article/1526502

 

主函数

int main ( int argc, char** argv )
{
    if ( argc != 3 )
    {
        cout<<"usage: triangulation img1 img2"<<endl;
        return 1;
    }
    //-- 读取图像
    Mat img_1 = imread ( argv[1], CV_LOAD_IMAGE_COLOR );
    Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );

    vector<KeyPoint> keypoints_1, keypoints_2;
    vector<DMatch> matches;
    find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
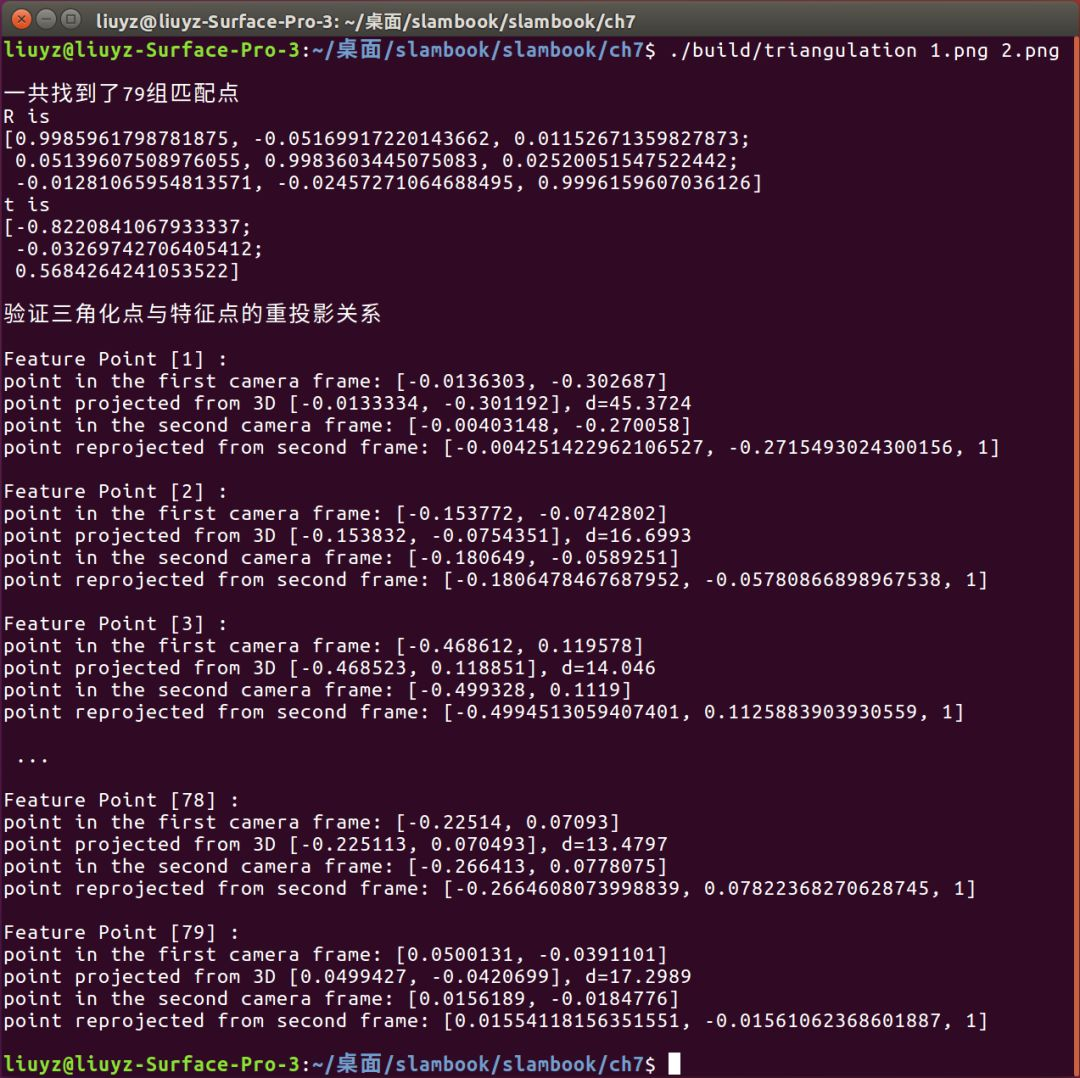
    cout<<"一共找到了"<<matches.size() <<"组匹配点"<<endl;

    //-- 估计两张图像间运动
    Mat R,t;
    pose_estimation_2d2d ( keypoints_1, keypoints_2, matches, R, t );
    //此外，在主函数中调用triangulation函数时，直接用对极约束求得的归一化R，t（||t||=1）当作真实的R，t，求得的是该R、t下的相机深度。在实际运用的时候应该是给定确定的R、t来求深度的

    //-- 三角化
    vector<Point3d> points;
    triangulation( keypoints_1, keypoints_2, matches, R, t, points );
    
    //-- 验证三角化点与特征点的重投影关系
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    for ( int i=0; i<matches.size(); i++ )
    {
        Point2d pt1_cam = pixel2cam( keypoints_1[ matches[i].queryIdx ].pt, K );
        Point2d pt1_cam_3d(
            points[i].x/points[i].z, 
            points[i].y/points[i].z 
        );
        
        cout<<"point in the first camera frame: "<<pt1_cam<<endl;
        cout<<"point projected from 3D "<<pt1_cam_3d<<", d="<<points[i].z<<endl;
        
        // 第二个图
        Point2f pt2_cam = pixel2cam( keypoints_2[ matches[i].trainIdx ].pt, K );
        Mat pt2_trans = R*( Mat_<double>(3,1) << points[i].x, points[i].y, points[i].z ) + t;
        pt2_trans /= pt2_trans.at<double>(2,0);
        cout<<"point in the second camera frame: "<<pt2_cam<<endl;
        cout<<"point reprojected from second frame: "<<pt2_trans.t()<<endl;
        cout<<endl;
    }

    //

//-- 验证三角化点与特征点的重投影关系
Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
Mat img1_plot = img_1.clone();
Mat img2_plot = img_2.clone();
for (int i = 0; i < matches.size(); i++) {
// 第一个图
float depth1 = points[i].z;
cout << "depth: " << depth1 << endl;
Point2d pt1_cam = pixel2cam(keypoints_1[matches[i].queryIdx].pt, K);
cv::circle(img1_plot, keypoints_1[matches[i].queryIdx].pt, 2, get_color(depth1), 2);

// 第二个图
Mat pt2_trans = R * (Mat_<double>(3, 1) << points[i].x, points[i].y, points[i].z) + t;
float depth2 = pt2_trans.at<double>(2, 0);
cv::circle(img2_plot, keypoints_2[matches[i].trainIdx].pt, 2, get_color(depth2), 2);
}
cv::imshow("img 1", img1_plot);
cv::imshow("img 2", img2_plot);
cv::waitKey();

    
    return 0;
}

　　

前后两帧图像对应两种不同的验证方式：

• 前一帧图像，先将特征点的2d坐标投影到归一化平面坐标，再将三角化得到的3d坐标除以其深度信息来计算其归一化坐标（这里可以看出来三角化处理得到的3d坐标是位于前一帧相机坐标系下的），并进行对比；
• 后一帧图像，同样是先将特征点的2d坐标投影到归一化平面坐标，再将前一帧相机坐标系下的3d点进行R、t位姿变换，计算出特征点在当前帧相机坐标系下的坐标，再除以其深度值来计算归一化坐标，进而进行比较。（79对特征点对共比较了79次，在结果展示时我会截取一部分。）

依赖函数

void find_feature_matches (
    const Mat& img_1, const Mat& img_2,
    std::vector<KeyPoint>& keypoints_1,
    std::vector<KeyPoint>& keypoints_2,
    std::vector< DMatch >& matches );

void pose_estimation_2d2d (
    const std::vector<KeyPoint>& keypoints_1,
    const std::vector<KeyPoint>& keypoints_2,
    const std::vector< DMatch >& matches,
    Mat& R, Mat& t );

void triangulation (
    const vector<KeyPoint>& keypoint_1,
    const vector<KeyPoint>& keypoint_2,
    const std::vector< DMatch >& matches,
    const Mat& R, const Mat& t,
    vector<Point3d>& points
);

// 像素坐标转相机归一化坐标
Point2f pixel2cam( const Point2d& p, const Mat& K );

其中，find_feature_matches这个函数已经是老生常谈，功能是用来求取两帧图像中的特征点并进行特征点匹配；

pose_estimation_2d2d函数用来以2d-2d方式求取相机位姿变化（因为只有不知道特征点的3d信息时才需要三角测量进行深度值的计算）；

pixel2cam函数用来将特征点的像素坐标转换成归一化平面坐标。

这里，只有triangulation函数是一个新面孔，在这里阅读以下形参信息，可以预测其功能是通过已知的特征点2d坐标与特征点配对信息，以及刚求解得到的相机位姿变化，来求取特征点的3d坐标。这里3d坐标是在前一帧还是当前帧的相机坐标系下的，咱们过会读代码可以做出确定。　

 

 函数triangulation的定义

void triangulation ( 
    const vector< KeyPoint >& keypoint_1, 
    const vector< KeyPoint >& keypoint_2, 
    const std::vector< DMatch >& matches,
    const Mat& R, const Mat& t, 
    vector< Point3d >& points )
{
    Mat T1 = (Mat_<float> (3,4) <<
        1,0,0,0,
        0,1,0,0,
        0,0,1,0);
    Mat T2 = (Mat_<float> (3,4) <<
        R.at<double>(0,0), R.at<double>(0,1), R.at<double>(0,2), t.at<double>(0,0),
        R.at<double>(1,0), R.at<double>(1,1), R.at<double>(1,2), t.at<double>(1,0),
        R.at<double>(2,0), R.at<double>(2,1), R.at<double>(2,2), t.at<double>(2,0)
    );
    
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    vector<Point2f> pts_1, pts_2;
    for ( DMatch m:matches )
    {
        // 将像素坐标转换至相机坐标
        pts_1.push_back ( pixel2cam( keypoint_1[m.queryIdx].pt, K) );
        pts_2.push_back ( pixel2cam( keypoint_2[m.trainIdx].pt, K) );
    }
    
    Mat pts_4d;
    cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );
    
    // 转换成非齐次坐标
    for ( int i=0; i<pts_4d.cols; i++ )
    {
        Mat x = pts_4d.col(i);
        x /= x.at<float>(3,0); // 归一化
        Point3d p (
            x.at<float>(0,0), 
            x.at<float>(1,0), 
            x.at<float>(2,0) 
        );
        points.push_back( p );
    }
}

　　首先，将平移矩阵t放到旋转矩阵R右侧，增广成3×4的变换矩阵，这里这个变换矩阵更具体来讲为projection matrix（投影矩阵）；进而使用pixel2cam将两组2d特征点的像素坐标转化成归一化平面坐标；最后，调用OpenCV提供的三角化处理函数triangulatePoints:

Mat pts_4d;
cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );

　　这里提供一下OpenCV中的函数声明：

void triangulatePoints(
   InputArray projMatr1,
   InputArray projMatr2, 
   InputArray projPoints1,
   InputArray projPoints2, 
   OutputArray points4D
);

　

　其中，由于以前一帧为参考，则前一帧到前一帧本身的投影矩阵projMatr1为3×3的单位阵与三维零列向量构成的增广阵；当前帧到参考帧（前一帧）的投影矩阵projMatr2为R和t的增广。该函数无返回值，但会修改并存储一个4×n的Mat类矩阵points4d（本函数中为pts_4d）。

for ( int i=0; i<pts_4d.cols; i++ )
    {
        Mat x = pts_4d.col(i);
        x /= x.at<float>(3,0); // 归一化
        Point3d p (
            x.at<float>(0,0), 
            x.at<float>(1,0), 
            x.at<float>(2,0) 
        );
        points.push_back( p );
    }

　最后，通过循环，逐列提取pts_4d中每个特征点经过三角化计算得到的齐次坐标，由于其具有尺度不变性，需要通过归一化处理，最后取其前三维并压入存储特征点3d坐标的容器points。我们来看一下程序运行结果（为了简洁小绿剔除了一些输出信息）：　

 

 

 

4 BA优化

https://jiangren.work/2019/08/17/%E8%AF%A6%E8%A7%A3BA/

 

 

 

2. 求解BA

2.1 迭代求解