cereas学习（1）min(10-x)平方 - MKT-porter

http://ceres-solver.org/nnls_tutorial.html

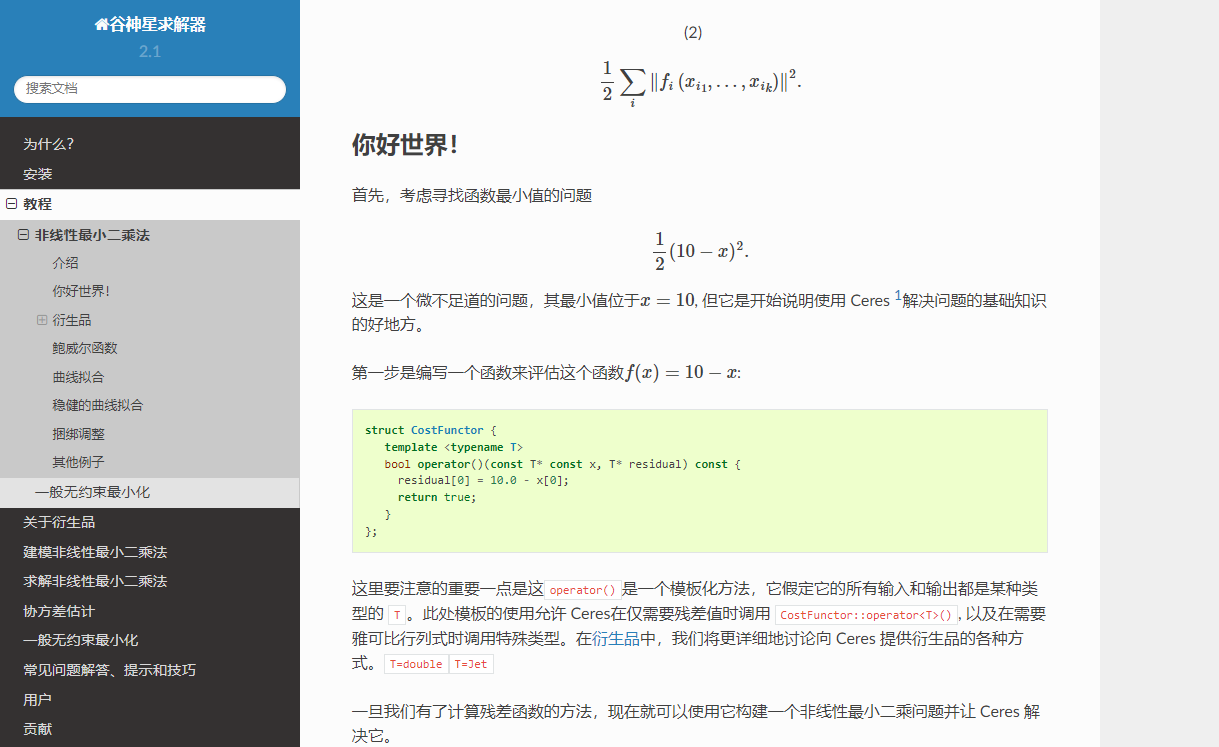
struct CostFunctor {
   template <typename T>
   bool operator()(const T* const x, T* residual) const {
     residual[0] = 10.0 - x[0];
     return true;
   }
};

　　这里要注意的重要一点是这operator()是一个模板化方法，它假定它的所有输入和输出都是某种类型的 T。此处模板的使用允许 Ceres在仅需要残差值时调用 CostFunctor::operator<T>(), 以及在需要雅可比行列式时调用特殊类型。在衍生品中，我们将更详细地讨论向 Ceres 提供衍生品的各种方式。T=doubleT=Jet

一旦我们有了计算残差函数的方法，现在就可以使用它构建一个非线性最小二乘问题并让 Ceres 解决它。

int main(int argc, char** argv) {
  google::InitGoogleLogging(argv[0]);

  // The variable to solve for with its initial value.
  double initial_x = 5.0;
  double x = initial_x;

  // Build the problem.
  Problem problem;

  // Set up the only cost function (also known as residual). This uses
  // auto-differentiation to obtain the derivative (jacobian).
  CostFunction* cost_function =
      new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
  problem.AddResidualBlock(cost_function, nullptr, &x);

  // Run the solver!
  Solver::Options options;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);

  std::cout << summary.BriefReport() << "\n";
  std::cout << "x : " << initial_x
            << " -> " << x << "\n";
  return 0;
}

AutoDiffCostFunction将 aCostFunctor作为输入，自动区分它并为其提供CostFunction 接口。

编译运行examples/helloworld.cc 给我们

iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  4.512500e+01    0.00e+00    9.50e+00   0.00e+00   0.00e+00  1.00e+04       0    5.33e-04    3.46e-03
   1  4.511598e-07    4.51e+01    9.50e-04   9.50e+00   1.00e+00  3.00e+04       1    5.00e-04    4.05e-03
   2  5.012552e-16    4.51e-07    3.17e-08   9.50e-04   1.00e+00  9.00e+04       1    1.60e-05    4.09e-03
Ceres Solver Report: Iterations: 2, Initial cost: 4.512500e+01, Final cost: 5.012552e-16, Termination: CONVERGENCE
x : 0.5 -> 10

从一个开始x=5，求解器在两次迭代中变为 10 2。细心的读者会注意到这是一个线性问题，一次线性求解应该足以得到最优值。求解器的默认配置是针对非线性问题的，为了简单起见，我们在这个例子中没有改变它。确实有可能在一次迭代中使用 Ceres 获得此问题的解决方案。另请注意，求解器在第一次迭代中确实非常接近最佳函数值 0。我们将在讨论 Ceres 的收敛和参数设置时更详细地讨论这些问题。

脚注

1个: 例子/helloworld.cc
2个: 实际上求解器运行了三次迭代，它通过查看线性求解器在第三次迭代中返回的值，观察到参数块的更新太小并宣布收敛。Ceres 仅在迭代结束时打印出显示，并在检测到收敛时立即终止，这就是为什么您在这里只看到两次迭代而不是三个。

#include "ceres/ceres.h"
#include "glog/logging.h"
using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solve;
using ceres::Solver;
// A templated cost functor that implements the residual r = 10 -
// x. The method operator() is templated so that we can then use an
// automatic differentiation wrapper around it to generate its
// derivatives.
//残差定义
struct CostFunctor {
  template <typename T>
  bool operator()(const T* const x, T* residual) const {
    residual[0] = 10.0 - x[0];
    return true;
  }
};
int main(int argc, char** argv) {
  google::InitGoogleLogging(argv[0]);
  // The variable to solve for with its initial value. It will be
  // mutated in place by the solver.
  //初始值
  double x = 0.5;
  const double initial_x = x;
  // Build the problem.
  Problem problem;
  // Set up the only cost function (also known as residual). This uses
  // auto-differentiation to obtain the derivative (jacobian).
  //<CostFunctor, 1, 1>  残差1 纬度  待优化变量1纬
  CostFunction* cost_function =
      new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
  problem.AddResidualBlock(cost_function, nullptr, &x);
  // Run the solver!
  Solver::Options options;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);
  std::cout << summary.BriefReport() << "\n";
  std::cout << "x : " << initial_x << " -> " << x << "\n";
  return 0;
}

/*
运行结果
iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  4.512500e+01    0.00e+00    9.50e+00   0.00e+00   0.00e+00  1.00e+04       0    5.33e-04    3.46e-03
   1  4.511598e-07    4.51e+01    9.50e-04   9.50e+00   1.00e+00  3.00e+04       1    5.00e-04    4.05e-03
   2  5.012552e-16    4.51e-07    3.17e-08   9.50e-04   1.00e+00  9.00e+04       1    1.60e-05    4.09e-03
Ceres Solver Report: Iterations: 2, Initial cost: 4.512500e+01, Final cost: 5.012552e-16, Termination: CONVERGENCE
x : 0.5 -> 10

*/

解析导数

在某些情况下，无法使用自动微分。例如，以封闭形式计算导数可能比依赖自动微分代码使用的链式法则更有效。

在这种情况下，可以提供您自己的残差和雅可比计算代码。为此，如果您在编译时知道参数和残差的大小，请定义CostFunctionor的子类。SizedCostFunction例如，这里是SimpleCostFunctionimplementsf(x)=10−x

class QuadraticCostFunction : public ceres::SizedCostFunction<1, 1> {
 public:
  virtual ~QuadraticCostFunction() {}
  virtual bool Evaluate(double const* const* parameters,
                        double* residuals,
                        double** jacobians) const {
    const double x = parameters[0][0];
    residuals[0] = 10 - x;

    // Compute the Jacobian if asked for.
    if (jacobians != nullptr && jacobians[0] != nullptr) {
      jacobians[0][0] = -1;
    }
    return true;
  }
};

SimpleCostFunction::Evaluate提供了的输入数组 parameters、residuals残差输出数组jacobians和 Jacobian 矩阵的输出数组。该jacobians数组是可选的，Evaluate预计会在它非空时进行检查，如果是这种情况，则用残差函数的导数值填充它。在这种情况下，由于残差函数是线性的，因此雅可比行列式是常数4。

从上面的代码片段可以看出，实现 CostFunction对象有点繁琐。我们建议，除非您有充分的理由自己管理雅可比计算，否则您可以使用AutoDiffCostFunctionor NumericDiffCostFunction来构建您的残差块。

#include <vector>
#include "ceres/ceres.h"
#include "glog/logging.h"
using ceres::CostFunction;
using ceres::Problem;
using ceres::SizedCostFunction;
using ceres::Solve;
using ceres::Solver;
// A CostFunction implementing analytically derivatives for the
// function f(x) = 10 - x.
class QuadraticCostFunction
    : public SizedCostFunction<1 /* number of residuals */,
                               1 /* size of first parameter */> {
 public:
  bool Evaluate(double const* const* parameters,
                double* residuals,
                double** jacobians) const override {
    double x = parameters[0][0];
    // f(x) = 10 - x.
    residuals[0] = 10 - x;
    // f'(x) = -1. Since there's only 1 parameter and that parameter
    // has 1 dimension, there is only 1 element to fill in the
    // jacobians.
    //
    // Since the Evaluate function can be called with the jacobians
    // pointer equal to nullptr, the Evaluate function must check to see
    // if jacobians need to be computed.
    //
    // For this simple problem it is overkill to check if jacobians[0]
    // is nullptr, but in general when writing more complex
    // CostFunctions, it is possible that Ceres may only demand the
    // derivatives w.r.t. a subset of the parameter blocks.
    if (jacobians != nullptr && jacobians[0] != nullptr) {
      jacobians[0][0] = -1;
    }
    return true;
  }
};
int main(int argc, char** argv) {
  google::InitGoogleLogging(argv[0]);
  // The variable to solve for with its initial value. It will be
  // mutated in place by the solver.
  double x = 0.5;
  const double initial_x = x;
  // Build the problem.
  Problem problem;
  // Set up the only cost function (also known as residual).
  CostFunction* cost_function = new QuadraticCostFunction;
  problem.AddResidualBlock(cost_function, nullptr, &x);
  // Run the solver!
  Solver::Options options;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);
  std::cout << summary.BriefReport() << "\n";
  std::cout << "x : " << initial_x << " -> " << x << "\n";
  return 0;
}

posted on 2023-01-03 00:43 MKT-porter 阅读(98) 评论(0) 收藏举报

刷新页面返回顶部