slam14(2-1) v1 概率论知识 期望 方差 协方差

 

1-1期望和方差

 https://zhuanlan.zhihu.com/p/64859161

 

期望(Expectation, or expected value)是度量一个随机变量取值的集中位置或平均水平的最基本的数字特征；

方差(Variance)是表示随机变量取值的分散性的一个数字特征。 方差越大，说明随机变量的取值分布越不均匀，变化性越强；方差越小，说明随机变量的取值越趋近于均值，即期望值。

 

 

 

一、期望和方差的运算性质

 

 

 

 

 

 

 

 

 

 

 

 

请注意这里是抽样分布，抽样分布和整体的方差是有区别的。

 

1-2证明样本方差除以n-1而不是n

https://blog.csdn.net/qq_39521554/article/details/79633207

 

 

总体方差（variance）：总体中变量离其平均值距离的平均。一组数据

样本方差（variance）：样本中变量离其平均值距离的平均。一组数据

 

 

 

 

 

 

 

 

 

 

总结一下：

分母是m-1的情况下，估计值是总体方差的无偏估计

分母是m的情况下，值是最大似然估计

分母是m+1的情况下，值是最小MSE（Mean Squared Error) 的估计

如果觉得样本够大，那么用m-1是不错的，因为在大样本下，参数的方差就算大一点儿也不会多多少，影响也不会大到哪儿去。

如果要保证信息利用充分，那我肯定选择最大似然估计的方差。如果样本数量较小，我就选择最小MSE，因为此时无偏性其实不是第一准则，因为无偏导致了大方差是不可取的行为。

 

3 协方差

https://blog.csdn.net/xiao_lxl/article/details/72730000

 

 

# 为什么需要协方差？

 

上面几个统计量看似已经描述的差不多了，但我们应该注意到，标准差和方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集，最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解更多，比如，一个男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊，嘿嘿~协方差就是这样一种用来度量两个随机变量关系的统计量，我们可以仿照方差的定义：

 

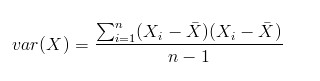
来度量各个维度偏离其均值的程度，标准差可以这么来定义：

 

 

协方差的结果有什么意义呢？如果结果为正值，则说明两者是正相关的(从协方差可以引出“相关系数”的定义)，也就是说一个人越猥琐就越受女孩子欢迎，嘿嘿，那必须的~结果为负值就说明负相关的，越猥琐女孩子越讨厌，可能吗？如果为0，也是就是统计上说的“相互独立”。

 

从协方差的定义上我们也可以看出一些显而易见的性质，如：

 

 

协方差多了就是协方差矩阵

上一节提到的猥琐和受欢迎的问题是典型二维问题，而协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算 n! / ((n-2)!*2) 个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

 

这个定义还是很容易理解的，我们可以举一个简单的三维的例子，假设数据集有三个维度，则协方差矩阵为

 

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。 

 

 

 

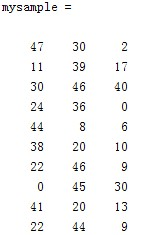
根据公式，计算协方差需要计算均值，那是按行计算均值还是按列呢，我一开始就老是困扰这个问题。前面我们也特别强调了，协方差矩阵是计算不同维度间的协方差，要时刻牢记这一点。样本矩阵的每行是一个样本，每列为一个维度，所以我们要按列计算均值。为了描述方便，我们先将三个维度的数据分别赋值：

 

原来协方差矩阵还可以这样计算，先让样本矩阵中心化，即每一维度减去该维度的均值，使每一维度上的均值为0，然后直接用新的到的样本矩阵乘上它的转置，然后除以(N-1)即可。其实这种方法也是由前面的公式推导而来，只不过理解起来不是很直观，但在抽象的公式推导时还是很常用的！

总结

 

理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差，而不是不同样本之间，拿到一个样本矩阵，我们最先要明确的就是一行是一个样本还是一个维度，心中明确这个整个计算过程就会顺流而下，这么一来就不会迷茫了~