https://www.zhihu.com/question/291275949
1数学基础
1-1 伴随性质




1-2 指数映射
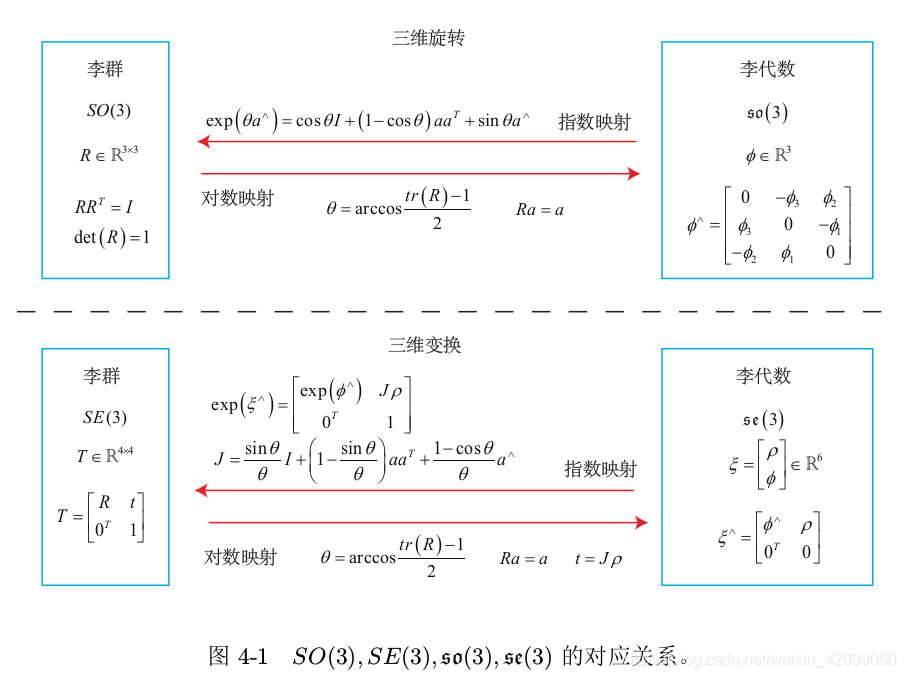
2 书上定义



2-1 变化量说明
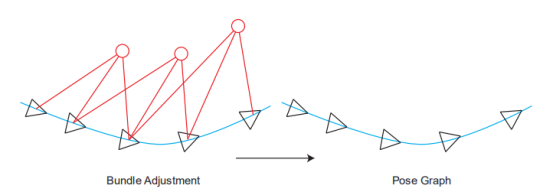
这就进入了第11讲,后端2。这章的内容依旧是实践为重点,我这里主要讲到的公式推导,因为我看的时候花了点时间,所以把它写下来。 BA和图优化,是把位姿和空间点放在一块,进行优化。特征点非常多,机器人轨迹越走越长,特征点增长的也很快。因此位姿图优化的意义在于:在优化几次以后把特征点固定住不再优化,只当做位姿估计的约束,之后主要优化位姿。
也就是说,不要红色的路标点了,只要位姿。位姿里的三角形是位姿,蓝色的线是两个位姿之间的变换。 【关于这点,有一个理解非常重要:三角形的位姿,是通过和世界坐标系的比较而得到的,其实世界坐标系在大部分情况下也就是一开机的时候的相机坐标系,把第一帧检测到的特征点的相机坐标,当成是世界坐标,以此为参照,逐步直接递推下去。而上图蓝色的线,是根据中途的两张图,单独拿它俩出来估计一个相对的位姿变换。 换言之:在前端的匹配中,基本都是世界坐标系的点有了,然后根据图像坐标系下的点,估计世界坐标系与图像坐标系下的变换关系作为位姿,(这里的世界坐标系下的坐标实际是根据第一帧一路递推下来的,可能错误会一路累积)我们假设算出来两个,分别是T1和T2。而蓝色的线,作为两个位姿之间的相对变换,也就是T1和T2之间的变换。但它并不是直接根据T1的逆乘以T2这种数学方式算出来的(不然还优化什么?肯定相等啊)而是通过T1和T2所在的图像进行匹配,比如单独算一个2D-2D之间的位姿变换或者光流法等,这样根据图像算出的位姿很有可能是和T1与T2用数学方式计算得到的位姿是有差异的(因为没有涉及到第一帧图像,就是单纯这两张图像的像素坐标)。这个理论一定要明白,不然纯粹是瞎学】 开始公式推导了,没看懂书上推导的可以看我这里的讲解: 先列一个李群的变换:

这个△的意思就是蓝色的边,两个位姿i和j之间的变换ij。 高博就把它乘到右边,那么左边就是1,求对数是0,通过这种方式来构造一个误差,使它为0:

最后再总结下:第一,先由两个位姿顶点Ti和Tj、一个位姿变换边Tij构成一个优化函数,第二,扰动该函数并对两个位姿顶点的扰动量求偏导,得到J,然后计算H,第三,根据H△x=g得到扰动量△x,并对原先俩位姿进行更新,实现优化。(这点总结比较重要,不想清楚的话很容易在繁琐的推导中迷失掉,因此这里我们又有了一个新的认识,“前端”关注的是光度误差与重投影误差之类的东西,而这里“后端”关注的是已经知道了不同的位姿T,如何整体对它进行调整,这也就更符合了“后端”的含义) 把所有的顶点和边都考虑进来,总的目标函数就是: 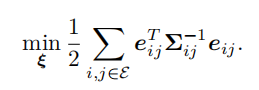
2-2 自我推导过程
https://www.guyuehome.com/18321

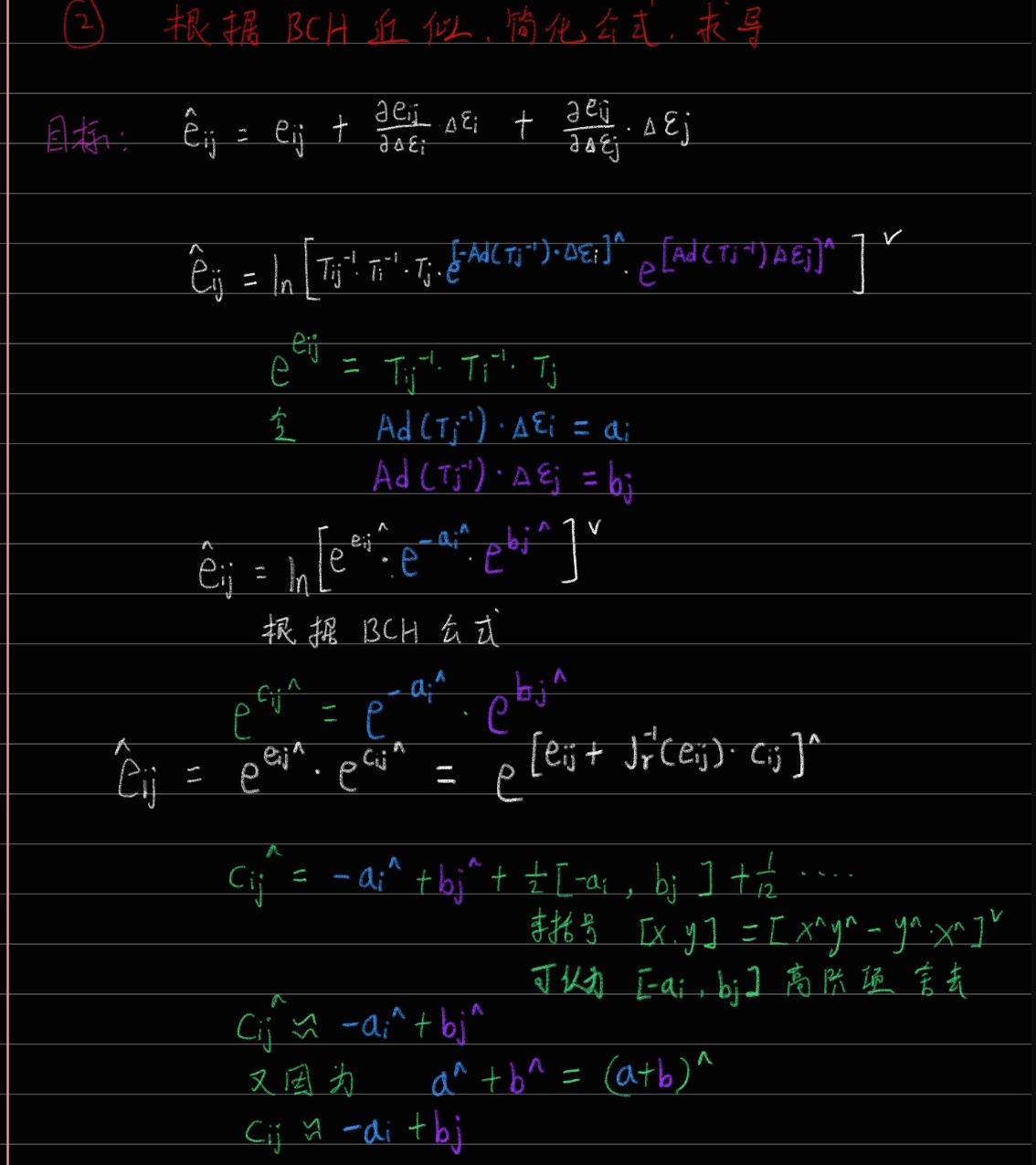
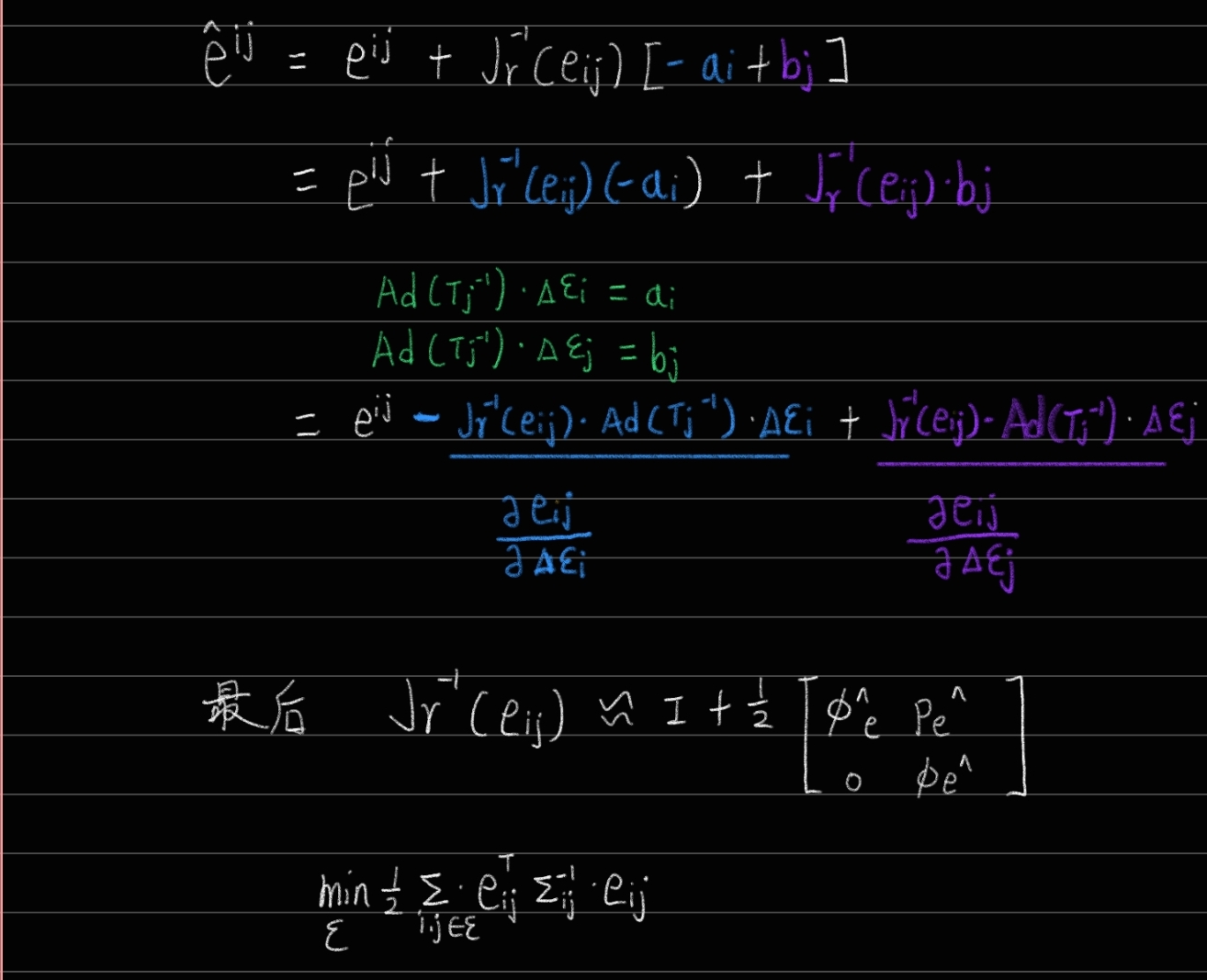
3 例子使用
3-1 网上例程学习
https://blog.csdn.net/weixin_46405486/article/details/122540859
一个帮助理解的例子:
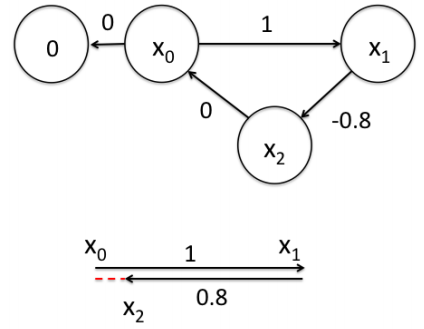
为了更好的理解这个过程,将用一个很好的例子作说明。如下图所示,假设一个机器人初始起点在0处,然后机器人向前移动,通过编码器测得它向前移动了1m,到达第二个地点。接着,又向后返回,编码器测得它向后移动了0.8米。但是,通过闭环检测,发现它回到了原始起点。可以看出,编码器误差导致计算的位姿和观测到有差异,那机器人这几个状态中的位姿到底是怎么样的才最好的满足这些条件呢?

首先构建位姿之间的关系,即图的边:
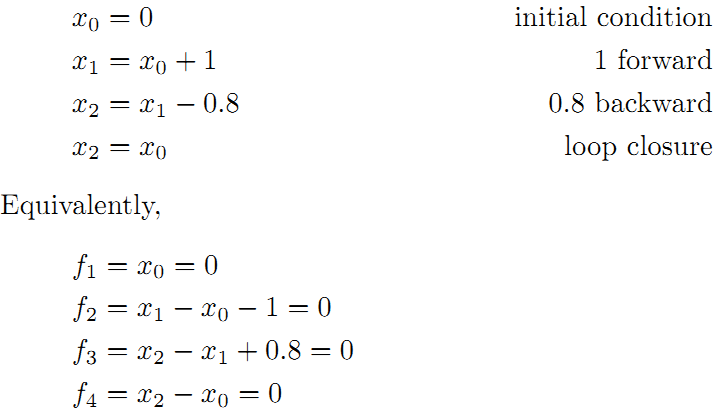
线性方程组中变量小于方程的个数,要计算出最优的结果,使出杀手锏最小二乘法。先构建残差平方和函数:

为了使残差平方和最小,我们对上面的函数每个变量求偏导,并使得偏导数等于0.
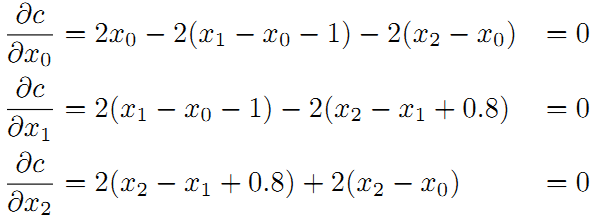
整理得到:
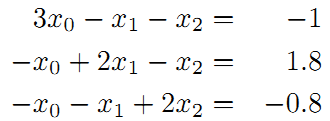
接着矩阵求解线性方程组:
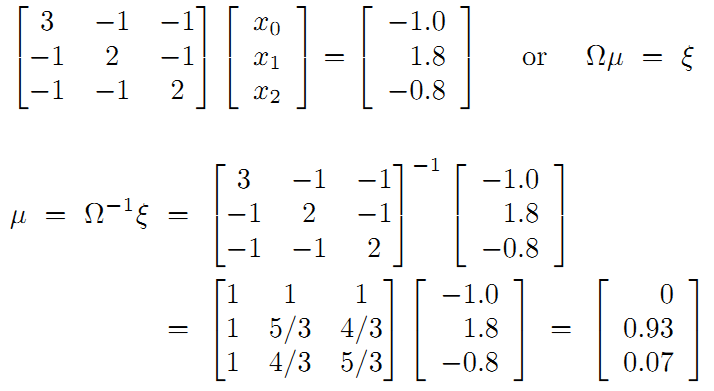
所以调整以后为满足这些边的条件,机器人的位姿为:
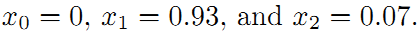
在这里例子中我们发现,闭环检测起了决定性的作用。
另一个例子:
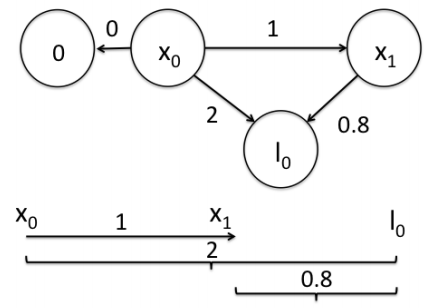
前面是用闭环检测,这次用观测的路标(landmark)来构建边。如下图所示,假设一个机器人初始起点在0处,并观测到其正前方2m处有一个路标。然后机器人向前移动,通过编码器测得它向前移动了1m,这时观测到路标在其前方0.8m。请问,机器人位姿和路标位姿的最优状态?
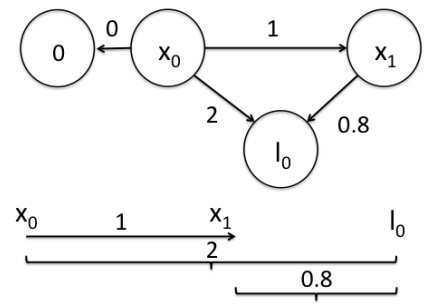
在这个图中,我们把路标也当作了一个顶点。构建边的关系如下:

即

残差平方和:
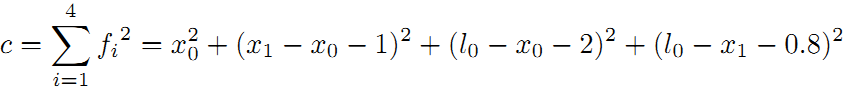
求偏导数:
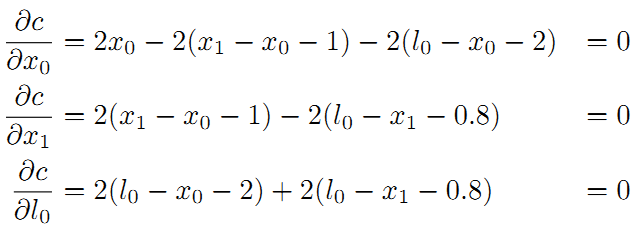
最后整理并计算得:
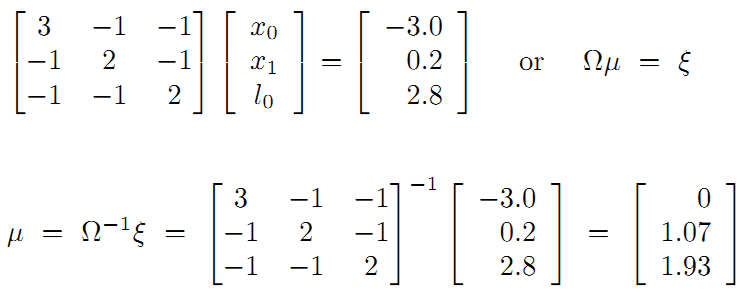
得到路标和机器人位姿:

接下来,将引入了一个重要的概念。我们知道传感器的精度是有差别的,也就是说我们对传感器的相信程度应该不同。比如假设这里编码器信息很精确,测得的路标距离不准,我们应该赋予编码器信息更高的权重,假设是10。重新得到残差平方和如下:
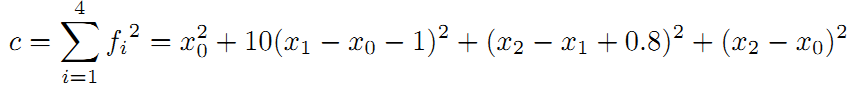
求偏导得:

转换为矩阵:

最后计算得到:
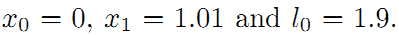
将这个结果和之前对比,可以看到这里的机器人位姿x1更靠近编码器测量的结果。请记住这种思想,这里的权重就是在后面将要经常提到的边的信息矩阵,在后面还将介绍。
图优化概念说明

图SLAM 和 EKF SLAM都是先进行预测,再进行估计,只是估计的方法有所不同:EKF是提取特征,投影到相机平面,再通过卡尔曼做更新;图SLAM是基于预测到的位置再估计观测的特征的位置,再和地图上的这个特征点的位置作比较(一般不重合),要么估计有问题,要么地图有问题,要么都有问题
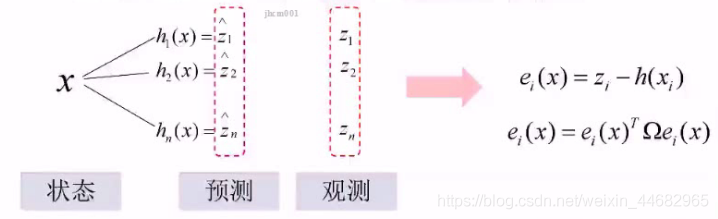
预测的特征点的位置和地图上的特征点的位置做差,优化预测的相机位置x,令差值最小(Ω是噪声,代表权重,噪声越大,权重应该越小)

landmark、相机状态作为顶点,可见链接为边(相机1能看见landmark1,所以相机1和landmark1有边;相机2能看见landmark1,所以相机2和landmark1有边;相机1和相机2都能看见landmark1,相机1和相机2有边),共同看到的特征点越多,变得权重越大。

Covisibility Graph
定义:由一系列相互可见的标志点和状态组成的无向链接


局部矫正:在很小的范围内(几帧)进行实时矫正
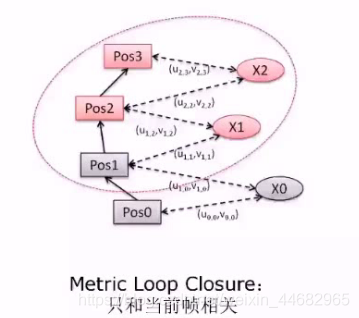
全局矫正:

https://blog.csdn.net/Hansry/article/details/78046342?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-1-78046342-blog-108552606.pc_relevant_multi_platform_whitelistv3&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-1-78046342-blog-108552606.pc_relevant_multi_platform_whitelistv3&utm_relevant_index=1







============================================================
3-2 自己将位姿优化应用于图优化推导
一个自身测量值 通过imu或者视觉定位得到的每一个节点的位姿。
一个是观测数值 通过回环或者观测路标点,观测到的位姿。
这两个位姿肯定不相等,因为有测量误差的存在,所有构建误差项,最小化总体误差,套用图优化,最后 求导f(x)'=0处的 x数值,就是最优的x位姿。
即为什么测量出的转换矩阵和理论计算的转换矩阵的误差err要这样计算?



3-3 graph slam tutorial :从推导到应用3
https://blog.csdn.net/heyijia0327/article/details/47428553

https://blog.csdn.net/heyijia0327/article/details/47428553
https://gitcode.net/mirrors/versatran01/graphslam?utm_source=csdn_github_accelerator

reference:
1. Grisetti的课程,有课件下载,点这里
2. Grisetti. 《A Tutorial on Graph-Based SLAM》
3. Grisetti. 课件 《SLAM Back-end》(可以直接搜到)
其他资料
一般pose图优化在帧多时用,分情况讨论pose图优化的代价函数:
代价函数已达极值,无需优化的情况:
- 没回环,无BA,用观测求解出前后帧相对pose
代价函数未达极值,可以优化的情况:
- 全局BA联合优化路标点与pose,联合优化后pose作为测量,注意BA联合优化了所有变量,当固定路标点时,pose仍有优化空间
- 局部BA联合优化路标点与pose,联合优化后局部pose作为测量,局部BA联合优化部分变量,而pose图优化所有pose变量,有更大的优化空间。
- 有回环,求出回坏帧的相对pose作为测量
个人以为这里的相对位姿一个是根据前端计算的位姿,也就是用特征点匹配或者光流或者类似kinectfusion那样或者利用灰度不变假设估计的位姿,如果仅仅有这一个位姿实际上是没有误差的,因为我们再计算每一帧的时候实际上都是计算相邻两帧之间的位姿变换,再将两帧之间的估计转换为相对全局的估计,实际上就是采用优化后的位姿取计算位姿图中边的相邻两帧的位姿。
但是一旦有回环检测到,那么就会出现两个位姿:1)根据相邻两帧之间的数据估计的位姿;2)根据回环检测计算的当前帧与上一关键帧相对运动的位姿,此时对于回环这一帧而言,其位姿就可能有两个不同的值了,因此构建位姿图可以进行优化,此时位姿图中也有环。
另一种情况是,使用基于所有数据的BA迭代几轮之后,计算相邻帧的相对位姿变换作为边,这时认为观测已经不怎么改变,也就是认为点的位置已经固定,则在应用schur技巧求解时可以忽略观测的边,仅仅利用位姿来求解,这时候的图也构成仅仅包含位姿作为节点、相对位姿作为边的图。此时也是仅对位姿进行优化,主要为降低求解时间,因为少解一个方程了,此时图中没有环,当然这样可能与pose graph通常认为的不一致,因为实际上观测数据还是在的,只不过并不去优化他们了,不过也有人把仅含有位姿的优化成为位姿图优化,因此这里也说明以下。
简而言之,位姿图中相对位姿变换与顶点位姿并不能直接地进行计算,就是直接地使用顶点位姿去计算边的相对位姿,再去优化,此时优化是没啥意义的,因为边的相对位姿也是用顶点的位姿去计算的。

以ORB-SLAM中的位姿图优化为例。首先位姿图优化发生在回环的时候。这个时候,受到回环影响的关键帧就有两个位姿:一个是回环前带有漂移的位姿,一个是回环后将这个漂移消去的位姿。
抛开它构建essential graph这些过程,ORB-SLAM在位姿图优化的时候,把回环前带有漂移的位姿作为了初值,但利用回环后的位姿计算了帧间的相对位姿作为约束,也就是测量值,来进行优化。
posegraph的 测量值 是约束就是 相对pose,优化的是 构建地图的过程中的 原始位置姿态(比如没有经过 闭环矫正)
约束就是 相对pose, 对于 非闭环的地方,就是两帧相对, 对于闭环的地方就是 当前帧和闭环帧或者 neigbor 之间的相对。
如果没有闭环,那么就没有误差需要优化, 存在闭环的时候的优化的是什么?
我们可以看到 当前帧和闭环帧 之间的相对(icp 或者 pnp 或者sim3 ), 以及 当前帧和闭环帧原始的相对pose,这两个肯定是有较大的差异的。
优化的目的就是 把这种差异 均摊到其他的相对中,最终把pose以及map变换之后得到粗略的闭环,然后经过gba 优化一下,得到最终结果,实用g2o或者ceres 一般优化的量是 原始位置姿态,得到的及果实经过pose graph 优化之后的位置姿态。
作者:David LEE
链接:https://www.zhihu.com/question/291275949/answer/971185316
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
https://www.bilibili.com/video/BV1Su411v7bA/?spm_id_from=333.788.recommend_more_video.10&vd_source=f88ed35500cb30c7be9bbe418a5998ca
https://www.bilibili.com/video/BV1qf4y1G7xR/?vd_source=f88ed35500cb30c7be9bbe418a5998ca
深入理解图优化与g2o:图优化篇
https://www.cnblogs.com/gaoxiang12/p/5244828.html
https://blog.csdn.net/qq_29462849/article/details/121326906?spm=1001.2101.3001.6650.13&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EOPENSEARCH%7ERate-13-121326906-blog-103601569.pc_relevant_multi_platform_whitelistv3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EOPENSEARCH%7ERate-13-121326906-blog-103601569.pc_relevant_multi_platform_whitelistv3&utm_relevant_index=14
II.非线性位姿图优化方法
每个位姿图都由节点和边组成。位姿图中的节点对应机器人在环境中的位姿,边代表它们之间的空间约束。相邻节点之间的边是里程约束,其余边表示闭环约束。这在图 2a 中可视化。位姿图优化的目标是找到一种节点配置,使位姿图中所有约束的最小二乘误差最小。一般来说,非线性最小二乘优化问题可以定义如下:


位姿 SLAM 更容易解决,因为它不构建环境地图。图公式化问题具有稀疏结构,因此计算速度更快。另一个优点是它对糟糕的初始猜测具有鲁棒性。位姿SLAM的缺点是一般对异常值不强健,当有很多假闭环时不收敛。此外,旋转估计使它成为一个困难的非凸优化问题,因此凸松弛会导致局部最小值问题,并且无法保证全局最优。在本节中,我们将简要描述基于非线性最小二乘法的优化框架,这些框架以位姿图的形式提供解决方案。
A.g2o
g2o [2] 是一个开源通用框架,用于优化可以定义为图的非线性函数。它的优点是易于扩展、高效且适用于广泛的问题。作者在 [2] 中指出,他们的系统可与其他最先进的算法相媲美,同时具有高度的通用性和可扩展性。他们通过利用稀疏连接和图的特殊结构、使用先进的方法来解决稀疏线性系统以及利用现代处理器的特性来提高效率。该框架包含三种不同的方法来解决 PGO、GaussNewton、Levenberg-Marquardt 和 Powell’s Dogleg。主要用于解决机器人中的SLAM问题和计算机视觉中的BA问题。ORB-SLAM ([16][17]) 使用 g2o 作为后端进行相机位姿优化,SVO [18] 将其用于视觉里程计。
B. Ceres
Ceres Solver [9] 是一个开源 C++ 库,用于建模和解决大型复杂优化问题。它主要致力于解决非线性最小二乘问题(BA和SLAM),但也可以解决一般的无约束优化问题。该框架易于使用、可移植且经过广泛优化,以提供具有低计算时间的解决方案质量。Ceres 旨在允许用户定义和修改目标函数和优化求解器。实现的求解器包括信任域求解器(Levenberg-Marquardt、Powell’s Dogleg)和线搜索求解器。由于它有许多优点,Ceres 被用于许多不同的应用程序和领域。OKVIS ([19] [20]) 和 VINS [21] 使用 Ceres 来优化定义为图的非线性问题。
C. GTSAM
GTSAM [6] 是另一个开源 C++ 库,它为机器人和计算机视觉应用实现传感器融合。它可用于解决 SLAM、视觉里程计和运动结构 (SfM) 中的优化问题。GTSAM 使用因子图 [22] 对复杂的估计问题进行建模,并利用它们的稀疏性来提高计算效率。它实现了 Levenberg-Marquardt 和 Gauss-Newton 风格的优化器、共轭梯度优化器、Dogleg 和 iSAM:增量平滑和建图。GTSAM 与学术界和工业界的各种传感器前端一起使用。例如,有一个 SVO [23] 的变体,它使用 GTSAM 作为视觉里程计的后端。
D. SE-Sync
SE-Sync [10] 是一种可证明正确的算法,用于在特殊欧几里得群上执行同步。它的目标是在给定节点之间相对变换的噪声测量值的情况下估计一组未知位姿(欧几里德空间中的位置和方向)的值。它们的主要应用是在 2D 和 3D 几何估计的背景下。例如,位姿图 SLAM(在机器人技术中)、相机运动估计(在计算机视觉中)和传感器网络定位(在分布式传感中)。作者在 [10] 中指出,SE-Sync 通过利用特殊欧几里得同步问题的新颖(凸)半定松弛直接搜索全局最优解来改进以前的方法,并且能够为找到的解生成正确性的计算证明。他们应用截断牛顿黎曼信任区域方法 [24] 来找到有效的位姿估计。
B. 基准数据集
有从[25]获得的六个二维位姿图、两个真实词图和四个在模拟中创建的图。INTEL 和 MIT 位姿图是真实世界的数据集,通过处理在西雅图英特尔研究实验室和 MIT Killian Court 收集的原始车轮里程计和激光测距传感器测量值而创建。M3500 位姿图是一个模拟的曼哈顿世界 [26]。M3500a、M3500b 和 M3500c 数据集是 M3500 数据集的变体,在相对方向测量中添加了高斯噪声。噪声的标准偏差分别为 0.1、0.2 和 0.3 rad。还有从[13]获得的六个三维数据集。位姿图 Sphere-a、Torus 和 Cube 是在模拟中创建的。Sphere-a 数据集是 [27] 中发布的一个具有挑战性的问题。其他三个位姿图是真实世界的数据集。Garage 数据集是在 [28] 中引入的,Cubicle 和 Rim 是使用 ICP 在来自佐治亚理工学院 RIM 中心的 3D 激光传感器的点云上获取的。所有这些位姿图都在图 1 中用它们的里程计和闭环约束进行了可视化。表 I 包含每个数据集的节点数和边数。这些数字决定了优化过程中参数的数量和问题的复杂程度。

https://blog.csdn.net/heroybc/article/details/106355948
1.位姿图
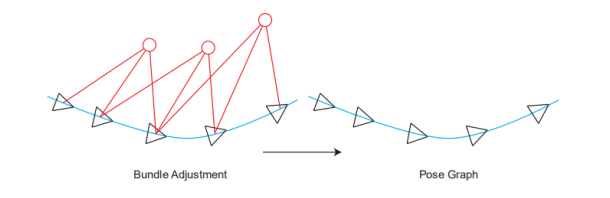
当把BA优化问题中的位姿图的问题简化要怎么做?
BA优化中的计算量很大很大,为了减少计算量,我已经介绍过很多方法了,这里,我们可以对位姿图进行优化,要如何做到,其实也很简单,只需要把相机观察的三维点去掉,在g2o优化问题上,只使用相机顶点,以及相邻相机顶点的关系描述即可。
这样,我们就大大简化了计算量,为啥这就简化计算量了呢,因为我们只考虑相机顶点,以及相邻相机顶点的关系,不考虑三维点了,我们知道,三维点的数量一定远远大于相机位姿顶点的数量。
数学

2.位姿优化
我们已经学习过李群李代数的知识了,我们知道优化问题的相关数学如下:
相对的位姿关系:

我们通过对积几何(平面投影)得到位姿变化1,又通过上式得到位姿变化2,我们要做的,就是减少位姿变化1与位姿变化1的误差,这是一个最小二乘问题。

为了优化两个位姿,求其偏导数:

得到雅可比矩阵后,就是用梯度法、牛顿法求解啦,相信大家到这里对于最小二乘问题已经轻车熟路了。
3.g2o图优化与位姿优化
我们先安装g2o并运行g2o。
//安装 git clone https://github.com/RainerKuemmerle/g2o/ git log |grep 8ba8a* git checkout 8ba8a03f7863e1011e3270bb73c8ed9383ccc2a2 sudo apt-get install libqt4-dev sudo apt-get install qt4-qmake sudo apt-get install libqglviewer-dev mkdir build cd build cmake ../ make -j8
李代数的位姿图优化
//展示部分片段,完整参考GITHUB
int main(int argc, char **argv) {
if (argc != 2) {
cout << "Usage: pose_graph_g2o_SE3_lie sphere.g2o" << endl;
return 1;
}
ifstream fin(argv[1]);
if (!fin) {
cout << "file " << argv[1] << " does not exist." << endl;
return 1;
}
// 设定g2o
typedef g2o::BlockSolver<g2o::blocksolvertraits<6, 6="">> BlockSolverType;
typedef g2o::LinearSolverEigen<blocksolvertype::posematrixtype> LinearSolverType;
auto solver = new g2o::OptimizationAlgorithmLevenberg(
g2o::make_unique<blocksolvertype>(g2o::make_unique<linearsolvertype>()));
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
int vertexCnt = 0, edgeCnt = 0; // 顶点和边的数量
vector<vertexse3liealgebra *=""> vectices;
vector<edgese3liealgebra *=""> edges;
while (!fin.eof()) {
string name;
fin >> name;
if (name == "VERTEX_SE3:QUAT") {
// 顶点
VertexSE3LieAlgebra *v = new VertexSE3LieAlgebra();
int index = 0;
fin >> index;
v->setId(index);
v->read(fin);
optimizer.addVertex(v);
vertexCnt++;
vectices.push_back(v);
if (index == 0)
v->setFixed(true);
} else if (name == "EDGE_SE3:QUAT") {
// SE3-SE3 边
EdgeSE3LieAlgebra *e = new EdgeSE3LieAlgebra();
int idx1, idx2; // 关联的两个顶点
fin >> idx1 >> idx2;
e->setId(edgeCnt++);
e->setVertex(0, optimizer.vertices()[idx1]);
e->setVertex(1, optimizer.vertices()[idx2]);
e->read(fin);
optimizer.addEdge(e);
edges.push_back(e);
}
if (!fin.good()) break;
}
cout << "read total " << vertexCnt << " vertices, " << edgeCnt << " edges." << endl;
cout << "optimizing ..." << endl;
optimizer.initializeOptimization();
optimizer.optimize(30);
cout << "saving optimization results ..." << endl;
// 因为用了自定义顶点且没有向g2o注册,这里保存自己来实现
// 伪装成 SE3 顶点和边,让 g2o_viewer 可以认出
ofstream fout("result_lie.g2o");
for (VertexSE3LieAlgebra *v:vectices) {
fout << "VERTEX_SE3:QUAT ";
v->write(fout);
}
for (EdgeSE3LieAlgebra *e:edges) {
fout << "EDGE_SE3:QUAT ";
e->write(fout);
}
fout.close();
return 0;
}


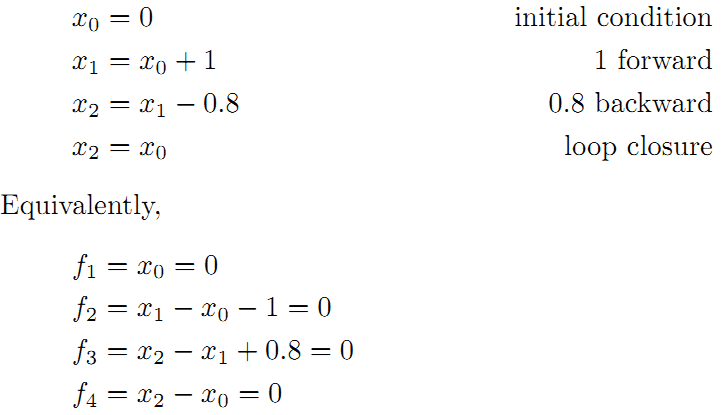
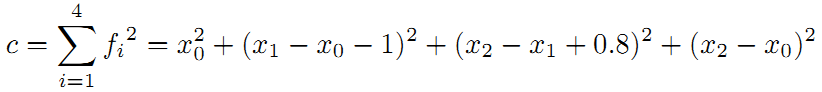
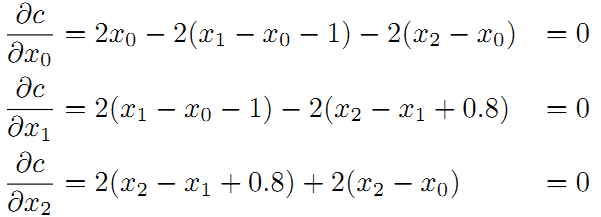
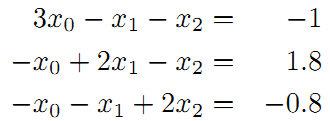
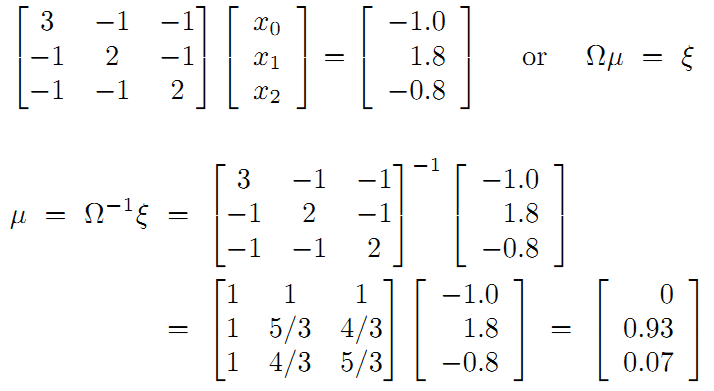
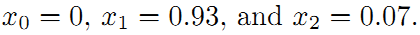

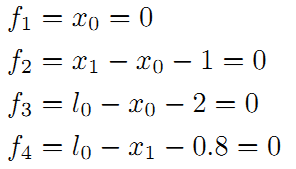

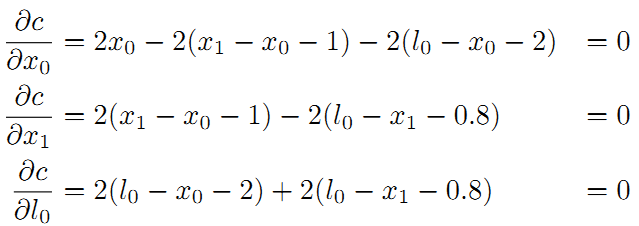
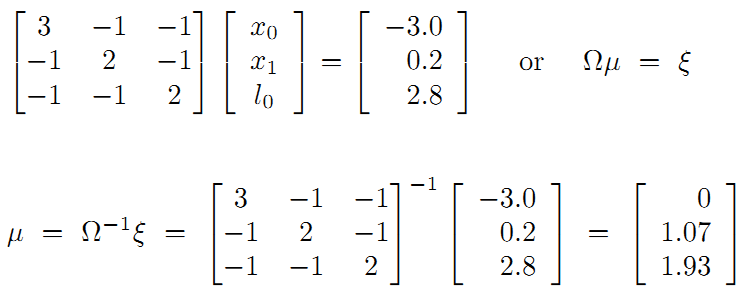
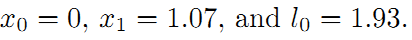
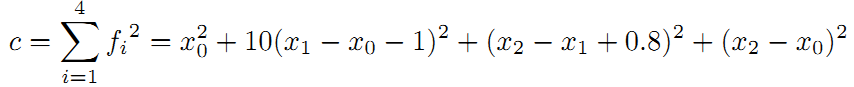
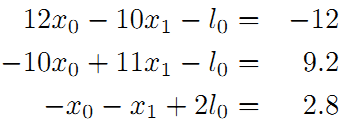
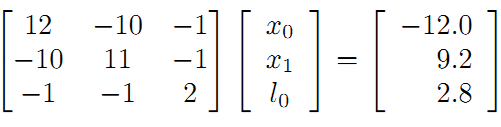


 浙公网安备 33010602011771号
浙公网安备 33010602011771号