1 讲解

https://zhuanlan.zhihu.com/p/557532018

李代数的引出

指数映射(exponential map)和对数映射(logarithmic map)

SO(3)上的指数映射

SE(3)上的指数映射

https://www.cnblogs.com/gaoxiang12/p/5577912.html

2书籍和详细的推导笔记

http://webhome.phy.duke.edu/~mehen/760/ProblemSets/BCH.pdf

https://blog.csdn.net/moyu123456789/article/details/93718232

全篇速览

1数学原理

1-1 矩阵乘法

乘法结合律： (AB)C=A(BC)．
乘法左分配律：(A+B)C=AC+BC
乘法右分配律：C(A+B)=CA+CB
对数乘的结合性k(AB）=(kA)B=A(kB）．
转置 (AB)T=BTAT．

矩阵乘法一般不满足交换律(除了有些特殊的方阵之间的乘法）。

满足乘法交换律的方阵称为可交换矩阵，即矩阵A，B满足：A·B=B·A。有以下几种情况：

(1) 设A , B 至少有一个为零矩阵,则A , B 可交换;

(2) 设A , B 至少有一个为单位矩阵, 则A , B可交换;

(3) 设A , B 至少有一个为数量矩阵, 则A , B可交换;

(4) 设A , B 均为对角矩阵,则A , B 可交换;

(5) 设A , B 均为准对角矩阵（准对角矩阵是分块矩阵概念下的一种矩阵。即除去主对角线上分块矩阵不为零矩阵外，其余分块矩阵均为零矩阵）,且对角线上的子块均可交换，则A , B 可交换;
例子

正常矩阵

反对称矩阵

叉乘的计算

1-2 矩阵指数乘法

矩阵乘法一般不满足交换律(除了有些特殊的方阵之间的乘法）

1-2-1 如果可以交换

https://www.cnblogs.com/gaoxiang12/p/5137454.html

2-1 SO(3)旋转矩阵映射

求解过程

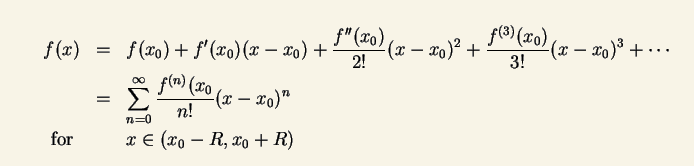
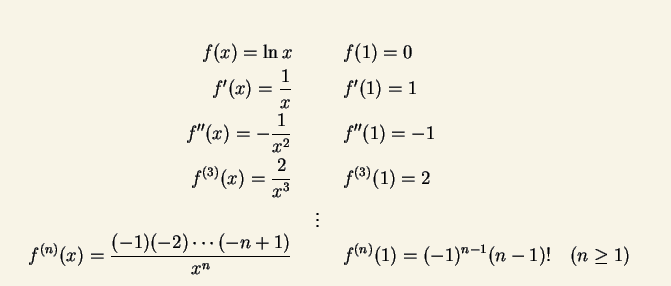
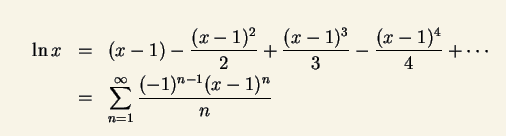
使得 n-1=t n=1开始 n=t+1 t=1开始替换n

2-2 SE(3)上的指数映射

https://zhuanlan.zhihu.com/p/33156814

（1）先给出SE(3)上的指数映射：
书上给的指数映射的式子就是这样，可是式A和式B是咋得到的呢？

（2）要证明的就是这个式A(指数映射)和式B(J式)：
式A的证明：

式B（J公式）的证明:

自己的手动证明过程

3李代数求导

3-0基础数学

求导就需要加法

但是旋转矩阵更新是乘法，经过SE3变换到E函数，想成变成相加。

但是相加是否可以直接按照一般的e函数相乘直接拆分成加法？？

3-1方法1 按照导数的定义求导 +

假设我们对一个空间点 $p$ 进行了一次旋转，得到了 $Rp$ ，现在为了优化我们的旋转 $R$ ，我们需要计算旋转后的点坐标，对旋转的导数，像是这样：

$\frac{\partial Rp}{\partial R} \\$

但是这个操作并不可行，因为 $SO(3)$ 并没有加法，所以这个式子其实应该是这样：

$\frac{\partial (exp(\phi^\wedge)p)}{\partial \phi} \\$

按照导数的定义：

其中

第二行是BCH公式的线性近似

第三行是泰勒展开后舍去高阶项的近似

第四第五行是将反对称符号看做两个向量的叉积（这点很容易证明），交换之后变号。

于是我们得到了旋转后的点对于李代数的导数。

3-2 方法2 左乘一个微小的扰动

SE(3)上的李代数求导

假设某空间点 $p$ ，经过一次变换 $T$ ，它和 $SO(3)$ 一样，也有对应的李代数：

$\xi ^\wedge = \begin{bmatrix} \phi\wedge &\rho \\ 0^T & 0 \end{bmatrix}\in \mathbb{R}^{4\times 4} \\$

它的李括号也类似 $\mathfrak{so}(3)$ ：

$[\xi_1,\xi_2] = (\xi_1^\wedge \xi_2^\wedge-\xi_2^\wedge \xi_1^\wedge)^\vee \\$

它对应的指数映射是：

$exp(\xi^\wedge) = \begin{bmatrix} \sum_{n=0}^{\infty }\frac{1}{n!}(\phi^\wedge)^n & \sum_{n=0}^{\infty }\frac{1}{(n+1)!}(\phi^\wedge)^n \rho \\ 0^T & 1 \end{bmatrix} \\=\begin{bmatrix} R & J\rho\\ 0^T & 1 \end{bmatrix} = T$

其中的 $\phi$ 就是之前旋转的李代数 $\mathfrak{so}(3)$ ，而 $\rho$ 表示平移（实际上 $t=J\rho$ ）， $J$ 是一个雅克比矩阵：

$J = \frac{sin\theta}{\theta}I+(1-\frac{sin\theta}{\theta})aa^T+\frac{1-cos\theta}{\theta}a^\wedge \\$

当我们添加一个左扰动 $\Delta T = exp(\Delta\xi^\wedge)$ ，则：

$\frac{\partial (exp(\xi^\wedge)p)}{\partial \Delta\xi} \\=\lim_{\Delta \xi \rightarrow 0} \frac{exp(\Delta \xi^\wedge)p-exp(\phi^\wedge)p}{\Delta \xi} \\ \approx \lim_{\Delta \xi \rightarrow 0} \frac{(1+\Delta \xi^\wedge)exp(\xi^\wedge)p-exp(\xi^\wedge)p}{\Delta \xi} \\=\lim_{\Delta \xi \rightarrow 0}\frac{\Delta \xi^\wedge exp(\xi^\wedge)p}{\Delta \xi} \\=\lim_{\Delta \xi \rightarrow 0} \frac{\begin{bmatrix}\Delta \phi^\wedge & \Delta\rho\\ 0^T & 0 \end{bmatrix}\begin{bmatrix}exp(\phi^\wedge)+t\\1 \end{bmatrix}}{\Delta\xi} \\=\lim_{\Delta \xi \rightarrow 0} \frac{\begin{bmatrix} \Delta\phi^\wedge(exp(\phi^\wedge)p+t)+\Delta\rho\\ 0\end{bmatrix}}{\Delta\xi} \\= \begin{bmatrix} I &-(Rp+t)^\wedge \\ 0^T & 0^T \end{bmatrix}$

推导过程

由此我们知道了三维点在旋转或变换之后的坐标，对位姿（旋转+平移）的导数，这样在后面计算Bundle Adjustment的时候，就不用担心无法求得位姿的导数，也就能够求取最小二乘法优化问题中对应的雅克比矩阵或者海塞矩阵，从而求解增量方程 $H\Delta x = g$ ，进而迭代更新啦！

posted on 2022-06-25 18:57 MKT-porter 阅读(191) 评论(0) 收藏举报

刷新页面返回顶部