slam14(1) v1_3_1 四元数基本知识

 

0定义

 

https://zhuanlan.zhihu.com/p/38067368

 

 

1-0用四元数表示旋转

 

 

 

 

 

 

1-1 旋转矩阵R与旋转向量a的关系：

 

 

 

 

定义旋转向量  ,写成叉乘的形式：  ，于是写成相应的李代数的旋转矩阵有：

最后由带入正弦、余弦的泰勒展开式，可得到 Rodrigues等式：

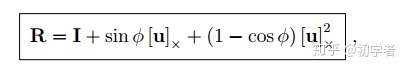
也可以写成：

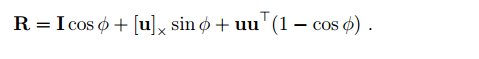
那么我们怎么由  呢，直接给出下面公式：

 

 

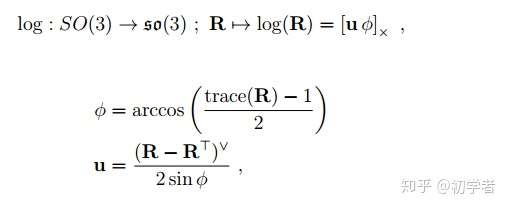
1-2 旋转向量a和四元数q关系

 

 

 

 

 

1-3 旋转矩阵和四元数关系

 

 

 

1-4旋转群与四元数的关系

纯四元数的指数形式为：

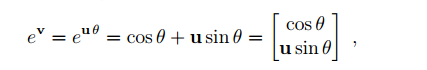
而对于单位四元素的定义：

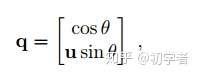
所以可以简单理解为一个纯四元数的指数就等于一个单位四元数。对于三维空间的旋转向量  ，

R=e^(&u)

 

 

 四元数李群李代数的表格

 

 

 

 

https://zhuanlan.zhihu.com/p/38043148

 

 

 

 

 

 

 

四元数的指数形式：

 

 

 

四元数的对数：

 

 

 

一般性知识 

https://www.qiujiawei.com/understanding-quaternions/

 

几何化展示含义

https://www.zhihu.com/question/23005815

 

 

 

 

 

四元数和旋转(Quaternion & rotation)

 

前提知识

 

 

https://zhuanlan.zhihu.com/p/78987582

定义

 

 

 

 

 

四元数的加减

和复数类似，四元数也可以被加减：

 

四元数的积

自己相乘= -1

其他轴反方向变换= -1

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.4 四元数表示旋转

 

 

 

 转换中用到的基本转换 

 

证明 思想

其中v为单位向量，左边叉乘的结果一定是与p和v共面的，且与v垂直的，因为平面和法向量是一一对应的。再看下图，证毕。

 

 

 

 

 

 

 旋转向量转化为四元数

 

四元数转化为旋转向量

 

 

 四元数连乘转换

 

3.5 四元数转换为旋转矩阵

 

 

 

 

 

 

四元数用于插值平滑

https://www.qiujiawei.com/understanding-quaternions/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

总结

除了特别难理解之外，相比矩阵或欧拉角，四元数在表示旋转这个事情上，拥有一些明显的优点。

• SLERP和SQUAD，提供了一种使得在朝向之间可以平滑过渡的方法。

• 使用四元数来串联"旋转"，要比使用矩阵快得多。

• 对于单位四元数，逆向旋转可以通过对向量部分取反来实现。而计算一个矩阵的逆矩阵是被认为比较慢的，如果这个矩阵未被标准正交化的话(标准正交矩阵的逆矩阵是它的转置矩阵)。

• 从四元数转换到矩阵，要比从欧拉角转换到矩阵快一点。

• 四元数只需要4个数字(如果旋转四元数已经单位化了那么只需要3个，实数部分可以在运行时计算)来表示一个旋转，而矩阵需要至少9个数字。

尽管使用四元数有这么多优点，还是有缺点存在的。

• 因为浮点数的舍入运算错误，四元数可能会变无效。不过，这个错误可以通过重新单位化四元数来避免。

• 使用四元数最具威慑性的地方，还是四元数的理解难度大。我希望这个问题可以通过阅读本文来解决。

存在一些已经实现了四元数、并且是正确的的数学程序库。在我的个人经验里，我发现GLM(OpenGL Math Library)是一个优秀的数学库，它的四元数的实现极其不错。如果你对在你的程序中使用四元数感兴趣，那么我会推荐你使用这个数学库。

 

 https://www.cnblogs.com/21207-iHome/p/6952004.html

四元数插值与均值（姿态平滑）

 

 

 四元数的球面线性插值（Slerp）

 

 

 

 

 

 

 

 

• 当p和q的夹角θ差非常小时会导致sinθ→0，这时除法可能会出现问题。为了避免这样的问题，当θ非常小时可以使用简单的线性插值代替（θ→0时，sinθ≈θ，因此方程退化为线性方程：slerp(p,q,t)=(1-t)p+tq）