eigen3安装

老版本
安装命令下载的是3.2版本的eigen 从而无法与模板类的sophus相匹配
sudo apt-get install libeigen3-dev
额外说明：
一个库由头文件和库文件组成。Eigen头文件的默认位置在 “usr/include/eigen3” 中。如果不确定，可以输入以下命令查找：
sudo updatedb
locate eigen3

新版本
(0) 卸载老版本年
sudo rm -rf /usr/include/eigen3 /usr/lib/cmake/eigen3 /usr/share/doc/libeigen3-dev /usr/share/pkgconfig/eigen3.pc /var/lib/dpkg/info/libeigen3-dev.list /var/lib/dpkg/info/libeigen3-dev.md5sums

（1）在官网（http://eigen.tuxfamily.org/index.php?title=Main_Page）下载安装包：eigen-3.3.7.tar.bz2 ，然后提取到此处
（2）进入文件夹eigen-3.3.7，右键在终端打开。
（3）进行安装

mkdir build

cd build

cmake ..

sudo make install

Eigen头文件的默认位置在 “/usr/local/include/eigen3”

指定路径

cd eigen-3.3.7
mkdir -p build && cd build
cmake \
    -DCMAKE_BUILD_TYPE=Release \
    -DCMAKE_INSTALL_PREFIX=/usr/local \
    ..
make -j4
make install

eigen3引用

CMakeLists.txt

# cmake needs this line
cmake_minimum_required(VERSION 3.1)

# Define project name
project(Eigen3_example_project)

find_package(Eigen3 REQUIRED)

#include_directories(${EIGEN3_INCLUDE_DIRS})
include_directories("/usr/local/include/eigen3") #自己编译的库


# Declare the executable target built from your sources
add_executable(Eigen3_example example.cpp)

# Eigen3就是一堆头文件没有连接库
#target_link_libraries(Eigen3_example PRIVATE ${OpenCV_LIBS})

第二种方式

CMakeLists.txt

cmake_minimum_required(VERSION 3.1)
project(untitled2)

set(CMAKE_CXX_STANDARD 11)
set(CMAKE_BUILD_TYPE Release)

set(ALL_TARGET_LIBRARIES "")


include(cmake/FindG2O.cmake)

#方式1
# find_package(Eigen3 REQUIRED)
# include_directories("/usr/local/include/eigen3")

#方式2 
include(cmake/FindEigen3.cmake)


add_executable(fit_curve fit_curve.cpp)
target_link_libraries(fit_curve ${ALL_TARGET_LIBRARIES})

或者导入安装包的位置文件

　　FindEigen3.cmake

# - Try to find Eigen3 lib
#
# This module supports requiring a minimum version, e.g. you can do
#   find_package(Eigen3 3.1.2)
# to require version 3.1.2 or newer of Eigen3.
#
# Once done this will define
#
#  EIGEN3_FOUND - system has eigen lib with correct version
#  EIGEN3_INCLUDE_DIR - the eigen include directory
#  EIGEN3_VERSION - eigen version

# Copyright (c) 2006, 2007 Montel Laurent, <montel@kde.org>
# Copyright (c) 2008, 2009 Gael Guennebaud, <g.gael@free.fr>
# Copyright (c) 2009 Benoit Jacob <jacob.benoit.1@gmail.com>
# Redistribution and use is allowed according to the terms of the 2-clause BSD license.

if(NOT Eigen3_FIND_VERSION)
  if(NOT Eigen3_FIND_VERSION_MAJOR)
    set(Eigen3_FIND_VERSION_MAJOR 2)
  endif(NOT Eigen3_FIND_VERSION_MAJOR)
  if(NOT Eigen3_FIND_VERSION_MINOR)
    set(Eigen3_FIND_VERSION_MINOR 91)
  endif(NOT Eigen3_FIND_VERSION_MINOR)
  if(NOT Eigen3_FIND_VERSION_PATCH)
    set(Eigen3_FIND_VERSION_PATCH 0)
  endif(NOT Eigen3_FIND_VERSION_PATCH)

  set(Eigen3_FIND_VERSION "${Eigen3_FIND_VERSION_MAJOR}.${Eigen3_FIND_VERSION_MINOR}.${Eigen3_FIND_VERSION_PATCH}")
endif(NOT Eigen3_FIND_VERSION)

macro(_eigen3_check_version)
  file(READ "${EIGEN3_INCLUDE_DIR}/Eigen/src/Core/util/Macros.h" _eigen3_version_header)

  string(REGEX MATCH "define[ \t]+EIGEN_WORLD_VERSION[ \t]+([0-9]+)" _eigen3_world_version_match "${_eigen3_version_header}")
  set(EIGEN3_WORLD_VERSION "${CMAKE_MATCH_1}")
  string(REGEX MATCH "define[ \t]+EIGEN_MAJOR_VERSION[ \t]+([0-9]+)" _eigen3_major_version_match "${_eigen3_version_header}")
  set(EIGEN3_MAJOR_VERSION "${CMAKE_MATCH_1}")
  string(REGEX MATCH "define[ \t]+EIGEN_MINOR_VERSION[ \t]+([0-9]+)" _eigen3_minor_version_match "${_eigen3_version_header}")
  set(EIGEN3_MINOR_VERSION "${CMAKE_MATCH_1}")

  set(EIGEN3_VERSION ${EIGEN3_WORLD_VERSION}.${EIGEN3_MAJOR_VERSION}.${EIGEN3_MINOR_VERSION})
  if(${EIGEN3_VERSION} VERSION_LESS ${Eigen3_FIND_VERSION})
    set(EIGEN3_VERSION_OK FALSE)
  else(${EIGEN3_VERSION} VERSION_LESS ${Eigen3_FIND_VERSION})
    set(EIGEN3_VERSION_OK TRUE)
  endif(${EIGEN3_VERSION} VERSION_LESS ${Eigen3_FIND_VERSION})

  if(NOT EIGEN3_VERSION_OK)

    message(STATUS "Eigen3 version ${EIGEN3_VERSION} found in ${EIGEN3_INCLUDE_DIR}, "
                   "but at least version ${Eigen3_FIND_VERSION} is required")
  endif(NOT EIGEN3_VERSION_OK)
endmacro(_eigen3_check_version)

if (EIGEN3_INCLUDE_DIR)

  # in cache already
  _eigen3_check_version()
  set(EIGEN3_FOUND ${EIGEN3_VERSION_OK})

else (EIGEN3_INCLUDE_DIR)

  # specific additional paths for some OS
  if (WIN32)
    set(EIGEN_ADDITIONAL_SEARCH_PATHS ${EIGEN_ADDITIONAL_SEARCH_PATHS} "C:/Program Files/Eigen/include" "C:/Program Files (x86)/Eigen/include")
  endif(WIN32)

  find_path(EIGEN3_INCLUDE_DIR NAMES signature_of_eigen3_matrix_library
      PATHS
      include
      ${EIGEN_ADDITIONAL_SEARCH_PATHS}
      ${KDE4_INCLUDE_DIR}
      PATH_SUFFIXES eigen3 eigen
    )

  if(EIGEN3_INCLUDE_DIR)
    _eigen3_check_version()
  endif(EIGEN3_INCLUDE_DIR)

  include(FindPackageHandleStandardArgs)
  find_package_handle_standard_args(Eigen3 DEFAULT_MSG EIGEN3_INCLUDE_DIR EIGEN3_VERSION_OK)

  mark_as_advanced(EIGEN3_INCLUDE_DIR)

endif(EIGEN3_INCLUDE_DIR)

include_directories(SYSTEM ${EIGEN3_INCLUDE_DIR})

#编译过程

mkdir build
cd build
cmake ..
make

./Eigen3_example

工程代码

测试例子1 基本矩阵创建和求解

example.cpp

#include <iostream>

using namespace std;

#include <ctime>
// Eigen 核心部分
#include <Eigen/Core>
// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>
//#include <Eigen/Eigen>

using namespace Eigen;





int main(){
   

  // 1声明一个2*3的float矩阵
  Matrix<float, 2, 3> matrix_23;



  
  // 2-1输入数据（初始化）
  matrix_23 << 1, 2, 3, 4, 5, 6;
  // 输出
  cout << "matrix 2x3 from 1 to 6: \n" << matrix_23 << endl;



  // 2-3用()访问矩阵中的元素
  cout << "print matrix 2x3: " << endl;
  for (int i = 0; i < 2; i++) {
    for (int j = 0; j < 3; j++) cout << matrix_23(i, j) << "\t";
    cout << endl;
  }


 
  // 2-4-1矩阵相乘
   // 定义矩阵 3*1
  Matrix<float, 3, 1> vd_3d;
  vd_3d << 3, 2, 1;//赋值
  //数据类型转换后相乘
  Matrix<float, 2, 1> result = matrix_23 * vd_3d;

  cout << matrix_23 << "*"<<  vd_3d<<'\n' << result.transpose() << endl;

  // 2-4-2矩阵相乘
  //定义矩阵  3*1
  Vector3d v_3d;//   Matrix<double, 3, 1> vd_3d;
  v_3d << 4, 5, 6;//赋值
  //直接相乘不用户数据转换
  Matrix<double, 2, 1> result2 = matrix_23.cast<double>() * v_3d;
  cout << matrix_23 << "*"<<  v_3d <<'\n' <<result2.transpose() << endl;



  // 3 一些矩阵运算
  // 四则运算就不演示了，直接用+-*/即可。
  Matrix3d matrix_33 = Matrix3d::Random();      // 随机数矩阵     Matrix<double, 3, 3> vd_3d;
  cout << "random matrix: \n" << matrix_33 << endl;
  cout << "transpose: \n" << matrix_33.transpose() << endl;      // 转置
  cout << "sum: " << matrix_33.sum() << endl;            // 各元素和
  cout << "trace: " << matrix_33.trace() << endl;          // 迹
  cout << "times 10: \n" << 10 * matrix_33 << endl;               // 数乘
  cout << "inverse: \n" << matrix_33.inverse() << endl;        // 逆
  cout << "det: " << matrix_33.determinant() << endl;    // 行列式


  // 4 特征值
  // 实对称矩阵可以保证对角化成功
  SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33); //转置*本身
  cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
  cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;


  const int MATRIX_SIZE=50;
  



  // 5解方程
  // 我们求解 matrix_NN * x = v_Nd 这个方程 求解x
  // N的大小在前边的宏里定义，它由随机数生成
  // 直接求逆自然是最直接的，但是求逆运算量大

  Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
  matrix_NN = matrix_NN * matrix_NN.transpose();  // 保证半正定
  Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);

  clock_t time_stt = clock(); // 计时
  // 方法1 直接求逆
  Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;//.inverse()  逆
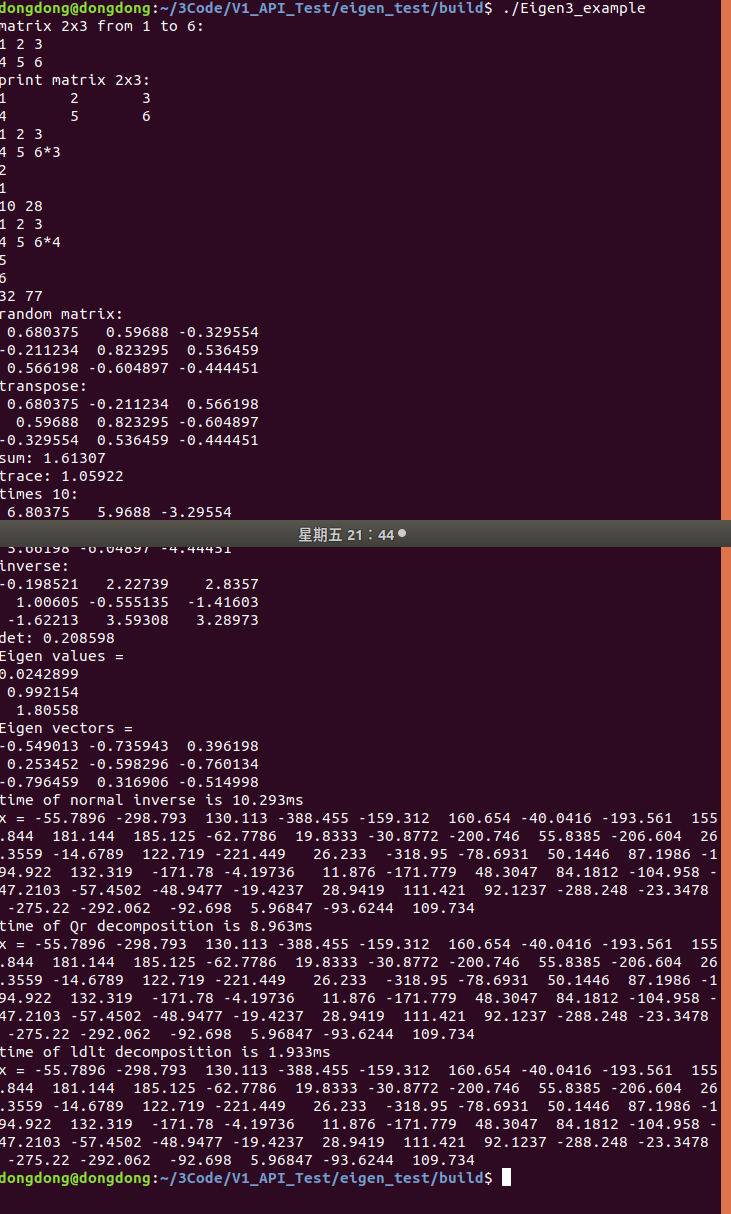
  cout << "time of normal inverse is "<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;//输出时间  8.408ms

  cout << "x = " << x.transpose() << endl;

  // 方法2  通常用矩阵分解来求，例如QR分解，速度会快很多
  time_stt = clock();
  x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
  cout << "time of Qr decomposition is "<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;//输出时间  8.849ms

  cout << "x = " << x.transpose() << endl;

  // 方法3 对于正定矩阵，还可以用cholesky分解来解方程
  time_stt = clock();
  x = matrix_NN.ldlt().solve(v_Nd);
  cout << "time of ldlt decomposition is " << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl; // 2.747ms

  cout << "x = " << x.transpose() << endl;



  return 0;
}

测试例子2

矩阵运算，欧拉角，旋转向量，旋转矩阵，坐标运算

#include <iostream>
#include <cmath>

using namespace std;

#include <Eigen/Core>
#include <Eigen/Geometry>

using namespace Eigen;

// 本程序演示了 Eigen 几何模块的使用方法

int main(int argc, char **argv) {

  // 0Eigen/Geometry 模块提供了各种旋转和平移的表示

  // 1-1  创建3D 旋转矩阵3*3 
  Matrix3d rotation_matrix = Matrix3d::Identity();//直接使用 Matrix3d 或 Matrix3f
  // 1-2  创建旋转向量3*1 
  // 使用 AngleAxis, 它底层不直接是Matrix，但运算可以当作矩阵（因为重载了运算符）
  AngleAxisd rotation_vector(M_PI / 4, Vector3d(0, 0, 1));     //沿 Z 轴旋转 45 度
  cout.precision(3);
  cout << "rotation matrix =\n" << rotation_vector.matrix() << endl;   //用matrix()转换成矩阵


  // 2-1 旋转向量 变换 旋转矩阵
  rotation_matrix = rotation_vector.toRotationMatrix();//3*3

  // 2-2 旋转矩阵 转换 欧拉角
  Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0);    // ZYX顺序，即roll pitch yaw顺序
  cout << "yaw pitch roll = " << euler_angles.transpose() << endl; // 


  // 3-1 坐标变换 旋转向量 rotation_vector * //欧拉角V
  Vector3d v(1, 0, 0);//欧拉角
  Vector3d v_rotated = rotation_vector * v;//
  cout << "(1,0,0) after rotation (by angle axis) = " << v_rotated.transpose() << endl;

  // 3-2 坐标变换 旋转矩阵 rotation_vector * //欧拉角V
  v_rotated = rotation_matrix * v;
  cout << "(1,0,0) after rotation (by matrix) = " << v_rotated.transpose() << endl;

  

  // 2-3创建 欧氏变换矩阵 使用 Eigen::Isometry
  Isometry3d T = Isometry3d::Identity();                // 虽然称为3d，实质上是4＊4的矩阵
  T.rotate(rotation_vector);                            // 按照rotation_vector进行旋转  旋转向量 rotation_vector
  T.pretranslate(Vector3d(1, 3, 4));                     // 把平移向量设成(1,3,4)
  cout << "Transform matrix = \n" << T.matrix() << endl;

/*

 0.707 -0.707      0      1
 0.707  0.707      0      3
     0      0      1      4
     0      0      0      1

*/

  // 3-3 用变换矩阵进行坐标变换
  Vector3d v_transformed = T * v;                              // 相当于R*v+t
  cout << "v tranformed = " << v_transformed.transpose() << endl;
 //v tranformed = 1.71 3.71    4



  // 对于仿射和射影变换，使用 Eigen::Affine3d 和 Eigen::Projective3d 即可，略

  // 2-4 旋转向量3*1 创建 四元数
  // 可以直接把AngleAxis赋值给四元数，反之亦然
  Quaterniond q = Quaterniond(rotation_vector);  //旋转向量 rotation_vector
  cout << "quaternion from rotation vector = " << q.coeffs().transpose() << endl;   // 请注意coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部
  //quaternion from rotation vector =     0     0 0.383 0.924

  // 2-5 旋转矩阵3*3 创建 四元数
  q = Quaterniond(rotation_matrix);
  cout << "quaternion from rotation matrix = " << q.coeffs().transpose() << endl;
  //quaternion from rotation matrix =     0     0 0.383 0.924

  // 3-4 使用四元数旋转一个向量，使用重载的乘法即可
  v_rotated = q * v; // 注意数学上是qvq^{-1}
  cout << "(1,0,0) after rotation = " << v_rotated.transpose() << endl;

  // 3-5 使用四元数旋转一个向量.用常规向量乘法表示，则应该如下计算
  /*
  向量   px=Quaterniond(0, 1, 0, 0)  -> 空间三维点（x,y,z）=(1,0,0)
  四元数输入 qx
  四元数结果 qy
  计算公式  py= q*px*(q^-1)  
  四元数结果转化为旋转矩阵
  .coeffs().transpose()
  
   */


  cout << "should be equal to " << (q * Quaterniond(0, 1, 0, 0) * q.inverse()).coeffs().transpose() << endl;

  return 0;
}

posted on 2021-05-31 16:11 MKT-porter 阅读(360) 评论(0) 收藏举报

刷新页面返回顶部