拆解 LLM 中的 SwiGLU
SwiGLU 作为一种高效的激活函数,近几年已被广泛应用于许多 LLM 中,例如 Llama 系列、DeepSeek LLM 和 Qwen 1.5 等。在了解 SwiGLU 之前,需要先了解它的几个重要 “前身”,即 Swish、SiLU 和 GLU 激活函数。
Swish
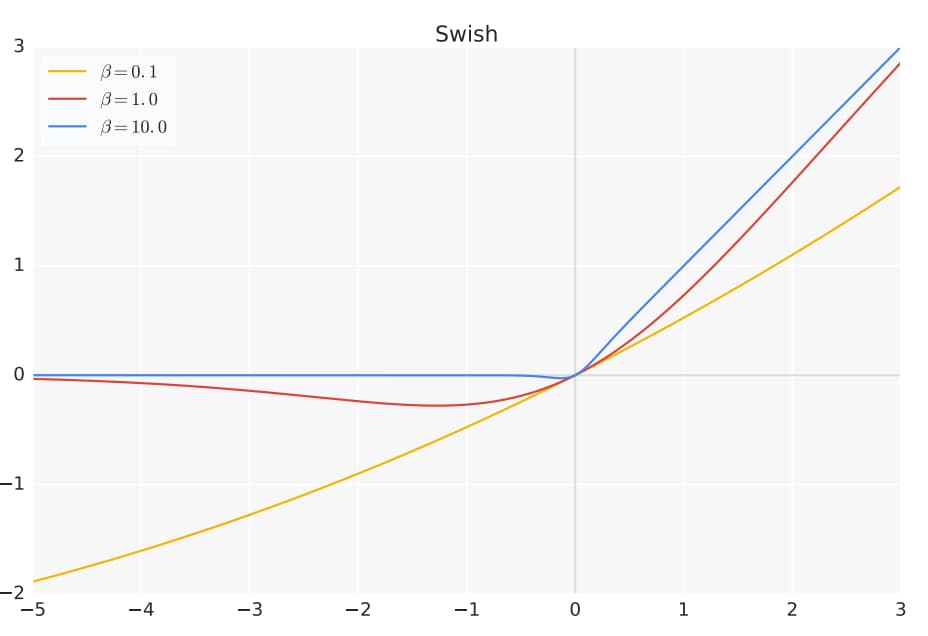
Swish 激活函数是由 Google Brain 团队在 2017 年提出的一种新型激活函数,其数学形式为:
$\text{Swish}(x) = x \cdot \sigma(\beta x) = x \cdot \frac{1}{1 + e^{-\beta x}}$
其中:
- $x$ 是输入值
- $\sigma(x)$ 是标准的 Sigmoid 函数
- $\beta$ 是一个可学习的参数或固定的超参数
- 当 $\beta = 0$ 时,$\text{Swish}$ 为线性函数 $f(x) = \frac{x}{2}$
- 当 $\beta = 1$ 时,$\text{Swish}$ 为 $\text{SiLU}$
- 当 $\beta \to \infty$ 时,$\text{Swish}$ 收敛为 $\text{ReLU}$
代码实现
def swish(x,beta=1.0): """Swish 激活函数 参数: x -- 输入值 返回: Swish 激活后的值 """ return x * sigmoid(beta*x)
特性
- 平滑性:Swish 函数是处处可导的平滑函数。这种平滑性有助于优化过程,使得梯度下降更加稳定。
- 非单调性:当输入 x 为负数时,Swish 的输出值会先下降到一个小的负值,然后再逐渐趋近于 0。这种非单调性可能有助于模型捕捉更复杂的模式。
- 无上界:当输入 x 趋向于正无穷时,Swish 的输出也趋向于正无穷。这有助于防止正向梯度饱和。
- 有下界:当输入 x 趋向于负无穷时,Swish 的输出趋近于 0(虽然它在小的负值区域会低于 0)。
- 自门控:Swish 可以看作是一种自门控机制。$\sigma(\beta x)$部分可以被视为一个“门”,它的值介于 0 和 1 之间,用来控制输入 x 有多少信息可以通过。当$\sigma(\beta x)$接近 1 时(对于大的正数 x),输出近似于 x(类似 ReLU);当$\sigma(\beta x)$接近 0 时(对于大的负数 x),输出近似于 0(也类似 ReLU)。但在中间区域,这个门控是平滑变化的。
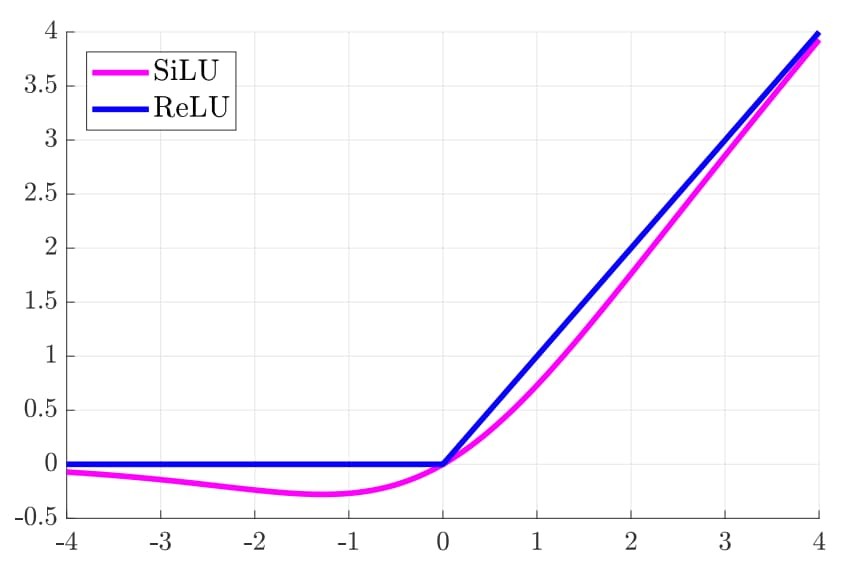
SiLU
当 Swish 激活函数中的 $\beta =1$ 时,Swish 变称为 SiLU 激活函数,数学公式为:
$\text{SiLU}(x) = x \cdot \frac{1}{1 + e^{-x}}$
GLU
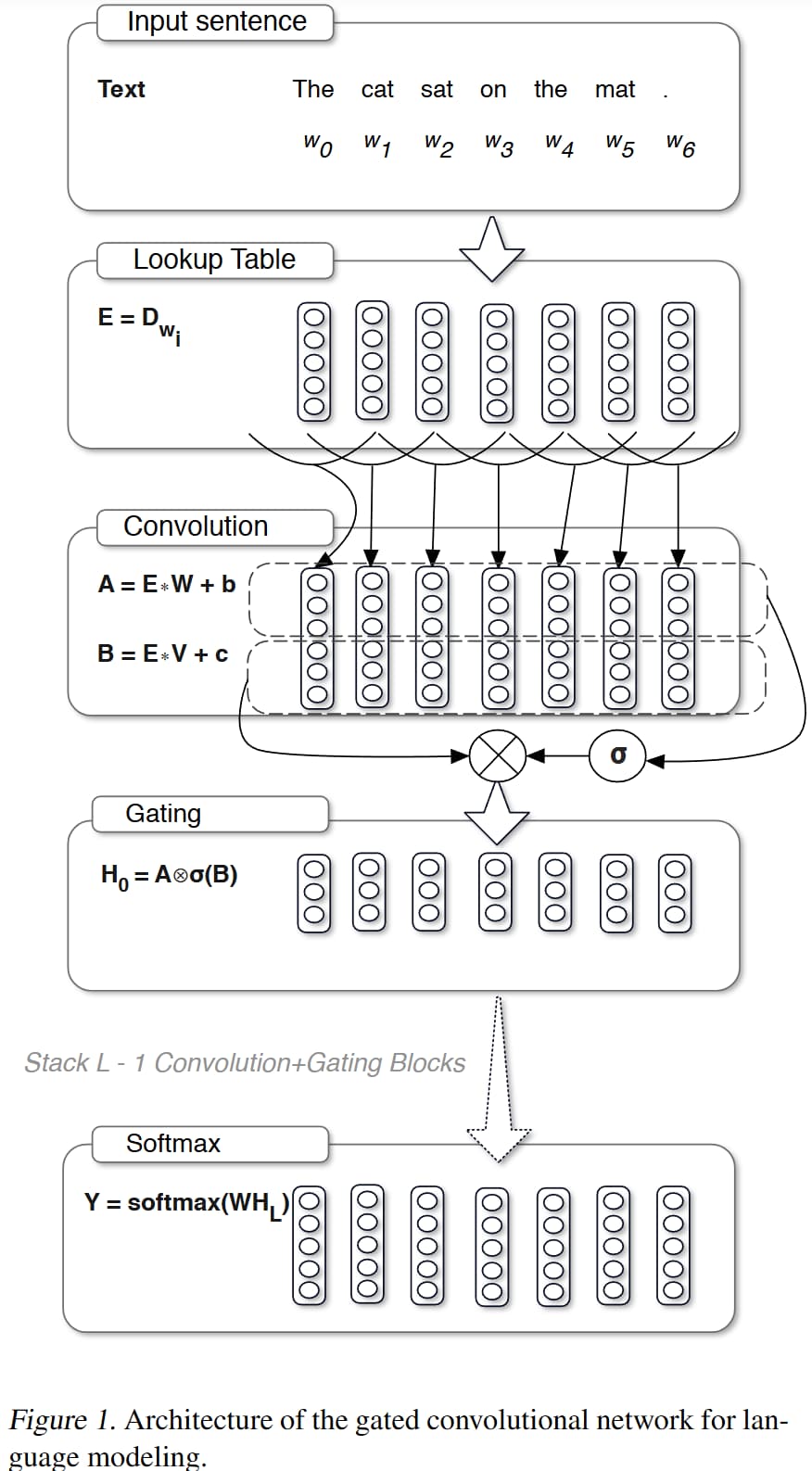
GLU 是由 Facebook AI Research 的 Dauphin 等人于 2017 年在论文《Language Modeling with Gated Convolutional Networks》中提出的。它本身更像是一个门控机制,通常结合线性变换使用,并作为网络层的一部分。
GLU 的核心思想是引入一个 “门” 来控制信息流。这个门的值是根据输入数据动态计算出来的,它决定了输入数据的哪一部分应该被传递下去,哪一部分应该被抑制。
GLU 作用在一个输入张量 X 上。通常,这个输入张量 X 会在某个维度(通常是最后一个特征维度或通道维度)上被分成两半,我们称之为 A 和 B。
然后,GLU 计算公式为:
$\text{GLU}(X) = A \odot \sigma(B)$
其中:
- $X$ 是输入张量
- $A$ 是张量 $X$ 的前半部分,$B$ 是张量 $X$ 的后半部分
- $\sigma$ 是 Sigmoid 函数
- $\odot$ 表示逐元素乘法(Hadamard 乘积)
代码实现
def GLU(x): """GLU 激活函数 参数: x -- 输入数组,维度必须是偶数 返回: GLU 激活后的数组 """ assert x.shape[-1] % 2 == 0, "输入数组的最后一个维度必须是偶数" half_dim = x.shape[-1] // 2 return x[..., :half_dim] * torch.sigmoid(x[..., half_dim:])
解释
- 输入分割:输入张量 X(通常是某个线性层或卷积层的输出)沿着指定的维度被平均分成两部分 A 和 B。这意味着,如果希望 GLU 的输出维度是 d,那么输入 X 的维度(在被分割的那个轴上)必须是 2d。
- 门计算:对其中一半 B 应用 Sigmoid 函数 σ(B)。这会为 B 中的每个元素生成一个介于 0 和 1 之间的值。这些值构成了“门”。
- 门控应用:将另一半 A 与计算得到的门 σ(B) 进行逐元素相乘。
- 如果 σ(B) 中的某个元素接近 1,那么对应的 A 中的元素将几乎完整地通过。
- 如果 σ(B) 中的某个元素接近 0,那么对应的 A 中的元素将被抑制,几乎变为 0。
- 如果 σ(B) 中的某个元素在 0.5 附近,则对应的 A 中的元素会被缩放。
- 输出:逐元素相乘的结果就是 GLU 的最终输出。注意,输出张量的维度(在被分割的那个轴上)是输入张量 X 的一半(即 A 或 B 的维度)。
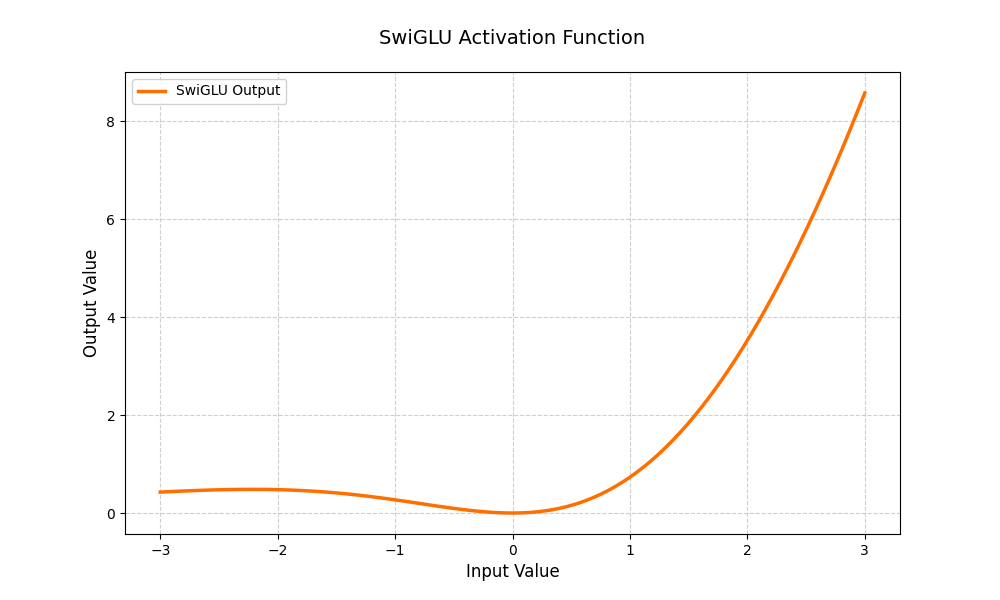
SwiGLU
SwiGLU 通常用在因果大语言模型的前馈网络层中,并表现出优于标准 ReLU 或 GELU 的性能。
具体公式如下:
代码实现
import numpy as np def SwiGLU(x): """SwiGLU 激活函数 参数: x -- 输入数组,维度必须是偶数 返回: SwiGLU 激活后的数组 """ assert x.shape[-1] % 2 == 0, "输入数组的最后一个维度必须是偶数" half_dim = x.shape[-1] // 2 return x[..., :half_dim] * swish(x[..., half_dim:])
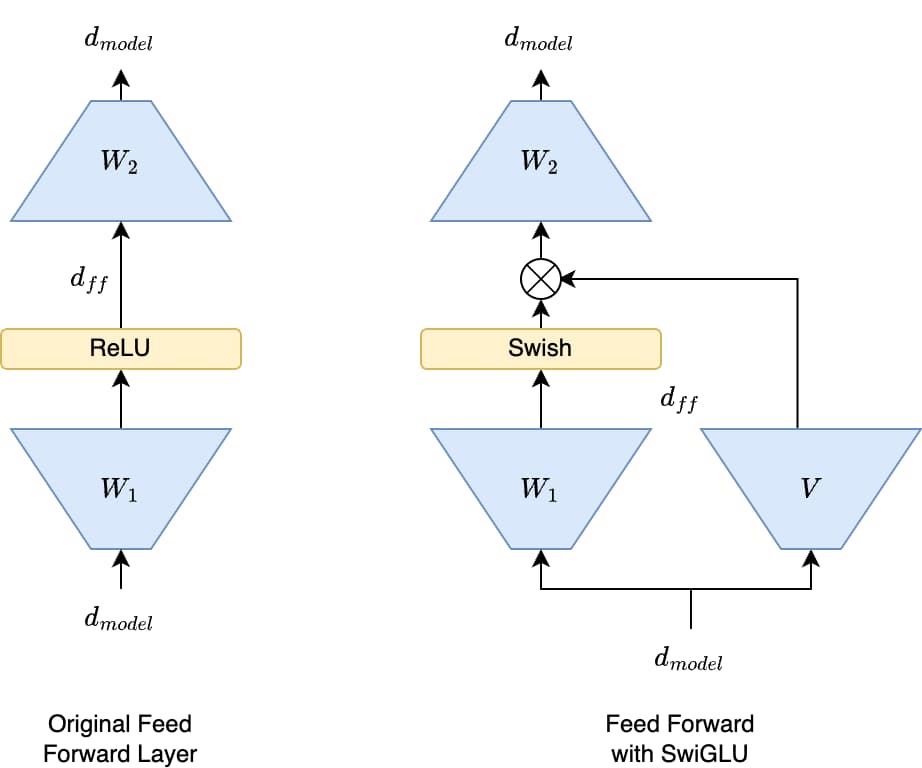
在 FFN 层中,SwiGLU 的应用通常不是像 GLU 那样简单地将一个大的线性层输出分割成两半。更常见的实现方式涉及三个线性变换。
假设 FFN 层的输入是 x(维度为 d_model),FFN 的中间隐藏层维度通常扩展到 d_ff。使用 SwiGLU 的 FFN 通常计算如下:
1. 两个并行的线性变换
- $\text{Gate} = W_{\text{gate}} \cdot x$
- $\text{Up} = W_{\text{up}} \cdot x$
- $W_{\text{gate}}$ 和 $W_{\text{up}}$ 都是将维度从 $\text{d\_model}$ 映射到 $\text{d\_ff}$ 的权重矩阵
2. 应用 $\text{Swish}$ 门控
- $\text{Gated} = \text{Swish}(\text{Gate}) \odot \text{Up}$
- $\text{Gated}$ 的维度是 $\text{d\_ff}$
3. 最终的线性变换
- $\text{Output} = W_{\text{down}} \cdot \text{Gated}$
- $W_{\text{down}}$ 是将维度从 $\text{d\_ff}$ 映射回 $\text{d\_model}$ 的权重矩阵
参数量计算
Transformer 的 FFN 有两个线性层,这两个线性层的参数量分别为:$d \times 4d$ 和 $4d \times d$,总的参数量为 $8d^2$。
从 $\text{SwiGLU}$ 公式中可以知道,因为按元素乘法操作,所以矩阵 $W_{\text{gate}}$ 与矩阵 $W_{\text{up}}$ 的维度是相同的,其作用是对输入向量 $x$ 进行升维;矩阵 $W_{\text{down}}$ 的作用是将高维的中间向量还原到和输入向量 $x$ 相同的维度。所以 $W_{\text{gate}}$、$W_{\text{up}}$、$W_{\text{down}}$ 这三个矩阵的维度分别为:$(d, \alpha d)$、$(d, \alpha d)$、$(\alpha d, d)$,总的参数量为 $3\alpha d^2$。为了保持和原始的 FFN 参数量相同,有: $$8d^2 = 3\alpha d^2$$
解得 $\alpha = \frac{8}{3}$,最终 $W_{\text{gate}}$、$W_{\text{up}}$、$W_{\text{down}}$ 这三个矩阵的维度分别为:$(d, \frac{8}{3}d)$、$(d, \frac{8}{3}d)$、$(\frac{8}{3}d, d)$,可以很明显的看出严格按照该公式计算出来的不是整数,所以使用该公式计算出来的是模型真实维度的近似值。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号