Flash Attenion算法原理
1 Flash Attention算法原理
1.1 Flash Attention Step-by-Step

1.2 Native Softmax
\( \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{k=1}^{N} e^{x_k}} \)
torch标准实现
import torch x = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) v = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) a = torch.softmax(x, dim = -1) o = a @ v print('x:', x) print('标准 Softmax a:', a) print('o:', o)
结果
x: tensor([1., 2., 3., 4., 5., 6.]) 标准 Softmax a: tensor([0.0043, 0.0116, 0.0315, 0.0858, 0.2331, 0.6337]) o: tensor(5.4329)
Native softmax算法分二次迭代:
- 计算 softmax 分母
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad d_i = d_{i-1} + e^{x_i} \end{aligned} \)
- 求对应位置的注意力Attention分数
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad a_i = \frac{e^{x_i}}{d_N} \end{aligned} \)
代码实现(分步)
# Native Softmax import torch l = 0 x = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) v = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) a = torch.zeros_like(x) # 计算 softmax 分母 for i in range(len(x)): l = l + torch.exp(x[i]) # 求对应位置的注意力Attention分数 for i in range(len(x)): a[i] = x[i].exp() / l o = a @ v print('x:', x) print('Native Softmax a:', a) print('o:', o)
结果
x: tensor([1., 2., 3., 4., 5., 6.]) Native Softmax a: tensor([0.0043, 0.0116, 0.0315, 0.0858, 0.2331, 0.6337]) o: tensor(5.4329)
1.3 Safe Softmax
原始softmax数值不稳定,改写成Safe Softmax版本
\( \text{softmax}(x_i) = \frac{e^{x_i} - max(x)}{\sum_{k=1}^{N} e^{x_k} - max(x) } \)
算法可以分成三次迭代来执行:
- 遍历所有数,求 x 中的最大值m
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad m_i = \max(m_i, x_i) \end{aligned} \)
- 计算 softmax 分母,并根据m对其进行缩放
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad d_i = d_{i-1} + e^{x_i - m_N} \end{aligned} \)
- 求对应位置的注意力Attention分数
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad a_i = \frac{e^{x_i - m_N}}{d_N} \end{aligned} \)
代码实现
# Safe Softmax import torch m = torch.tensor(-1000.0) l = 0 x = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) v = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) a = torch.zeros_like(x) # 遍历所有数,求 x 中的最大值m for i in range(len(x)): m = torch.max(m, x[i]) # 计算 softmax 分母,并根据m对其进行缩放 for i in range(len(x)): l += (x[i] - m).exp() # 求对应位置的注意力Attention分数 for i in range(len(x)): a[i] = (x[i]-m).exp() / l o = a @ v print('x:', x) print('Safe Softmax a:',a) print('o:', o)
结果
x: tensor([1., 2., 3., 4., 5., 6.]) Safe Softmax a: tensor([0.0043, 0.0116, 0.0315, 0.0858, 0.2331, 0.6337]) tensor(5.4329)
1.3 Online Softmax
\( \begin{aligned} d_i' &= \sum_{j}^{i} e^{x_j - m_i} \\ &= \sum_{j}^{i-1} e^{x_j - m_i} + e^{x_i - m_i} \\ &= \sum_{j}^{i-1} e^{x_j - m_{i-1} + m_{i-1} - m_i} + e^{x_i - m_i} \\ &= \left( \sum_{j}^{i-1} e^{x_j - m_{i-1}} \right) e^{m_{i-1} - m_i} + e^{x_i - m_i} \\ &= d_{i-1}' e^{m_{i-1} - m_i} + e^{x_i - m_i} \end{aligned} \)
这个式子依赖于\( d_{i-1}' \),\( m_i \),\( m_{i-1} \)。那么就可以将softmax前两步合并到一起:
- 求 x 的最大值 m, 计算 softmax 的分母
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad m_i = \max(m_i, x_i) \\ &\quad d_i' = d_{i-1}' e^{m_{i-1} - m_i} + e^{x_i - m_i} \end{aligned} \)
- 求对应位置的 Attention分数
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad a_i = \frac{e^{x_i - m_N}}{d_N} \end{aligned} \)
以上的算法优化可以将3步合并变成2步,将softmax的时间复杂度降为\(O(n^2)\)。
Python代码实现
下面是一个简单的 Python 实现,展示了如何用 Online Softmax 处理数据流:
# Online Softmax import torch m = torch.tensor(-1000.0) # 最大值 l = 0 o = 0 x = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) v = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) a = torch.zeros_like(x) # 求 x 的最大值 m, 计算 softmax 的分母 for i in range(len(x)): m_pre = m m = torch.max(m, x[i]) l = l * (m_pre - m).exp() + (x[i] - m).exp() # 求对应位置的 Attention分数 for i in range(len(x)): a[i] = (x[i]-m).exp() / l o = a @ v print('x:', x) print('Online Softmax a:',a) print('o:', o)
结果
x: tensor([1., 2., 3., 4., 5., 6.]) online softmax a: tensor([0.0043, 0.0116, 0.0315, 0.0858, 0.2331, 0.6337]) tensor(5.4329)
2 Flash Attention By Online Softmax (tiling)
2.1 Algorithm Multi-pass Self-Attention
基于2-pass online softmax 可以写出 2-pass的Self-Attention
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad x_i \leftarrow Q[k,:] K^T[:,i] \\ &\quad m_i \leftarrow \max(m_i, x_i) \\ &\quad d_i' \leftarrow d_{i-1}' e^{m_{i-1} - m_i} + e^{x_i - m_i} \end{aligned} \)
\( \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad a_i \leftarrow \frac{e^{x_i - m_N}}{d_N'} \\ &\quad o_i \leftarrow o_{i-1} + a_i V[i,:] \end{aligned} \)
代码实现
# Online Softmax import torch m = torch.tensor(-1000.0) # 最大值 l = 0 o = 0 x = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) v = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) a = torch.zeros_like(x) for i in range(len(x)): m_pre = m m = torch.max(m, x[i]) l = l * (m_pre - m).exp() + (x[i] - m).exp() for i in range(len(x)): a[i] = (x[i]-m).exp() / l o = o + a[i] * v[i] print('x:', x) print('2-pass Online Softmax a:',a) print('o:', o)
结果
x: tensor([1., 2., 3., 4., 5., 6.]) 2-pass Online Softmax a: tensor([0.0043, 0.0116, 0.0315, 0.0858, 0.2331, 0.6337]) o: tensor(5.4329)
2.2 Algorithm Flash-Attention
首先将系数d改成迭代形式
\(o_i \leftarrow o_{i-1} + \frac{e^{x_i - m_N}}{d_N'} V[i,:]\)
\(o_i := \sum_{j=1}^{i} \left( \frac{e^{x_j - m_N}}{d_N'} V[j,:] \right)\)
\(o_i' = \left( \sum_{j=1}^{i} \frac{e^{x_j - m_i}}{d_i'} V[j,:] \right)\)
其中,前 \( i \)个元素的局部指数和 \( d_i' \) 和 局部最大值\( m_i \),所计算出的 \( o_i' \)为局部注意力输出。当\(i = N\)时,\( o_i = o_i' \)
将\( O_{i} \)改写成迭代形式
\(\begin{aligned} o_i' &= \sum_{j=1}^{i} \frac{e^{x_j - m_i}}{d_i'} V[j,:] \\ &= \left( \sum_{j=1}^{i-1} \frac{e^{x_j - m_{i-1} +m_{i-1} - m_{i}}}{d_i'} V[j,:] \right) + \frac{e^{x_i - m_i}}{d_i'} V[i,:] \\ &= \left( \sum_{j=1}^{i-1} \frac{e^{x_j - m_{i-1}}}{d_{i-1}'} \cdot e^{m_{i-1} - m_i} \cdot \frac{d_{i-1}'}{d_i'} V[j,:] \right) + \frac{e^{x_i - m_i}}{d_i'} V[i,:] \\ &= o_{i-1}' \cdot e^{m_{i-1} - m_i} \cdot \frac{d_{i-1}'}{d_i'} + \frac{e^{x_i - m_i}}{d_i'} V[i,:] \end{aligned}\)
此时就得到Flash Attention的one-pass迭代形式
\(\begin{aligned} &\text{for } i \to 1, N \text{ do} \\ &\quad x_i \leftarrow Q[k,:] K^T[:,i] \\ &\quad m_i \leftarrow \max(m_{i-1}, x_i) \\ &\quad d_i' \leftarrow d_{i-1}' e^{m_{i-1} - m_i} + e^{x_i - m_i} \\ &\quad o_i' \leftarrow o_{i-1}' \frac{d_{i-1}' e^{m_{i-1} - m_i}}{d_i'} + \frac{e^{x_i - m_i}}{d_i'} V[i,:] \\ &\text{end} \\ &O[k,:] \leftarrow o_N' \end{aligned}\)
代码实现
import torch m = torch.tensor(-1000.0) # 最大值 l = 0 o = 0 x = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) v = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) a = torch.zeros_like(x) for i in range(len(x)): m_pre = m l_pre = l m = torch.max(m, x[i]) l = l * (m_pre - m).exp() + (x[i] - m).exp() # a[i] = (x[i]-m).exp() / l o = o * (l_pre * (m_pre - m).exp() / l) + (x[i] - m).exp() * v[i] / l print('x:', x) # print('online softmax a:',a) print('o:', o)
结果
x: tensor([1., 2., 3., 4., 5., 6.])
o: tensor(5.4329)
2.3 Algorithm Flash-Attention(Tiling)
当有多条数据时可进一步改写,得到最终的Flash Attention形式,源码基于以下实现。
\(\begin{aligned} &\text{for } i \to 1 \# \text{tiles} \\ &\quad x_i \leftarrow Q[k,:] K^T[:, (i - 1)b: ib] \\ &\quad m_i^{\text{local}} = \max_{j=1}^b (x_i[j]) \\ &\quad m_i \leftarrow \max(m_{i - 1}, m_i^{\text{local}}) \\ &\quad d_i' \leftarrow d_{i - 1}' e^{m_{i - 1} - m_i} + \sum_{j=1}^b e^{x_i[j] - m_i} \\ &\quad o_i' = o_{i - 1}' \frac{d_{i - 1}' e^{m_{i - 1} - m_i}}{d_i'} + \sum_{j=1}^b \frac{e^{x_i[j] - m_i}}{d_i'} V[j + (i - 1)b, :] \\ &\text{end} \\ &O[k, :] \leftarrow o_N' \end{aligned}\)
\( O_i \)随着\( K,V \)经过不断地迭代,不断地更新\( O_i \),最终与标准场景下的的输出O保持一致。
import torch NEG_INF = -1e10 # -infinity EPSILON = 1e-10 Q_LEN = 2 K_LEN = 2 Q_BLOCK_SIZE = 1 # KV_BLOCK_SIZE = 1 Tr = Q_LEN // Q_BLOCK_SIZE Tc = K_LEN // KV_BLOCK_SIZE Q = torch.randn(1, 1, Q_LEN, 4, requires_grad=True).to(device='cpu') K = torch.randn(1, 1, K_LEN, 4, requires_grad=True).to(device='cpu') V = torch.randn(1, 1, K_LEN, 4, requires_grad=True).to(device='cpu') O = torch.zeros_like(Q, requires_grad=True) l = torch.zeros(Q.shape[:-1])[..., None] m = torch.ones(Q.shape[:-1])[..., None] * NEG_INF Q_BLOCKS = torch.split(Q, Q_BLOCK_SIZE, dim=2) K_BLOCKS = torch.split(K, KV_BLOCK_SIZE, dim=2) V_BLOCKS = torch.split(V, KV_BLOCK_SIZE, dim=2) O_BLOCKS = list(torch.split(O, Q_BLOCK_SIZE, dim=2)) l_BLOCKS = list(torch.split(l, Q_BLOCK_SIZE, dim=2)) m_BLOCKS = list(torch.split(m, Q_BLOCK_SIZE, dim=2)) for j in range(Tc): Kj = K_BLOCKS[j] Vj = V_BLOCKS[j] for i in range(Tr): Qi = Q_BLOCKS[i] Oi = O_BLOCKS[i] li = l_BLOCKS[i] mi = m_BLOCKS[i] S_ij = Qi @ Kj.transpose(2,3) m_block_ij, _ = torch.max(S_ij, dim=-1, keepdims=True) P_ij = torch.exp(S_ij - m_block_ij) l_block_ij = torch.sum(P_ij, dim=-1, keepdims=True) + EPSILON mi_new = torch.maximum(m_block_ij, mi) P_ij_Vj = P_ij @ Vj li_new = torch.exp(mi - mi_new) * li \ + torch.exp(m_block_ij - mi_new) * l_block_ij O_BLOCKS[i] = (li / li_new) * torch.exp(mi - mi_new) * Oi \ +(torch.exp(m_block_ij - mi_new) / li_new) * P_ij_Vj print(f'-----------Attn : Q{i}xK{j}---------') # print(O_BLOCKS[i].shape) print(O_BLOCKS[0]) print(O_BLOCKS[1]) print('\n') l_BLOCKS[i] = li_new m_BLOCKS[i] = mi_new O = torch.cat(O_BLOCKS, dim=2) l = torch.cat(l_BLOCKS, dim=2) m = torch.cat(m_BLOCKS, dim=2) print(O)
结果
-----------Attn : Q0xK0--------- tensor([[[[-0.7460, -0.4906, 0.8255, 0.6993]]]], grad_fn=<AddBackward0>) tensor([[[[0., 0., 0., 0.]]]], grad_fn=<SplitBackward0>) -----------Attn : Q1xK0--------- tensor([[[[-0.7460, -0.4906, 0.8255, 0.6993]]]], grad_fn=<AddBackward0>) tensor([[[[-0.7460, -0.4906, 0.8255, 0.6993]]]], grad_fn=<AddBackward0>) -----------Attn : Q0xK1--------- tensor([[[[-0.7637, -0.4576, 0.7968, 0.6991]]]], grad_fn=<AddBackward0>) tensor([[[[-0.7460, -0.4906, 0.8255, 0.6993]]]], grad_fn=<AddBackward0>) -----------Attn : Q1xK1--------- tensor([[[[-0.7637, -0.4576, 0.7968, 0.6991]]]], grad_fn=<AddBackward0>) tensor([[[[-0.7522, -0.4790, 0.8155, 0.6992]]]], grad_fn=<AddBackward0>) tensor([[[[-0.7637, -0.4576, 0.7968, 0.6991], [-0.7522, -0.4790, 0.8155, 0.6992]]]], grad_fn=<CatBackward0>)
使用标准attention进行验证
# Standard Attention O = torch.softmax ( Q @ K.transpose(2,3), dim = -1) @ V print(O)
输出结果一致
tensor([[[[-0.7637, -0.4576, 0.7968, 0.6991],
[-0.7522, -0.4790, 0.8155, 0.6992]]]], grad_fn=<CatBackward0>)
3 Flash Attention动画

前提:\(Q, K, V \in \mathbb{R}^{M \times d} \)矩阵在HBM上,SRAM的芯片大小为\( M \),其中\( N=5,d=3,M=59 \)。

设置块大小为\( B_c = \left\lceil \frac{M}{4d} \right\rceil = 4, B_r = \min\left( \left\lceil \frac{M}{4d} \right\rceil, d \right) = 3 \)。
作者希望Q、K、V和S的区块能放进SRAM。我认为B_c被设为M/4d,而S的大小是B_r x B_c,所以我们不希望B_r超过4d,否则S就放不下了。为了保险起见,我直接设B_c <= d,这样S占用的SRAM不会超过1/4。您也可以将B_r和B_c设为不同值,只要这四个矩阵能够匹配即可。
https://github.com/Dao-AILab/flash-attention/issues/618#issuecomment-1772034791

在HBM上初始化\( O = (0)_{N \times d} \in \mathbb{R}^{N \times d}, \ell = (0)_N \in \mathbb{R}^N, m = (-\infty)_N \in \mathbb{R}^N \)。
将 \( Q \) 划分为 \( T_r = \left\lfloor \frac{N}{B_r} \right\rfloor \) 个块 \( Q_1, \dots, Q_{T_r} \),每个块的大小为 \( B_r \times d \);并将 \( K \)、\( V \) 划分为 \( T_c = \left\lfloor \frac{N}{B_c} \right\rfloor \) 个块 \( K_1, \dots, K_{T_c} \) 和 \( V_1, \dots, V_{T_c} \),每个块的大小为 \( B_c \times d \)。

将\( O \)划分为 \(T_r\) 个块 \(O_1, \dots, O_{T_r}\),每个块的大小为 \(B_r \times d\);将\( l \)划分为 \(T_r\) 个块 \(l_1, \dots, l_{T_r}\),每个块的大小为 \(B_r\); 将\( m \)划分为 \(T_r\) 个块 \(m_1, \dots, m_{T_r}\),每个块的大小为 \(B_r\)。
第一次外层循环 \(\text{for } 1 \leq j \leq T_c \text{ do } \) 将\( K_j, V_j\)从HDM加载到SRAM。

第一次内层循环 \(\text{for } 1 \leq j \leq T_r \text{ do } \) 将\( Q_i, O_i, l_i, m_i \)从HDM加载到SRAM。

在芯片中,计算\( S_{ij} = Q_i K_j^{\text{T}} \in \mathbb{R}^{B_r \times B_c} \)

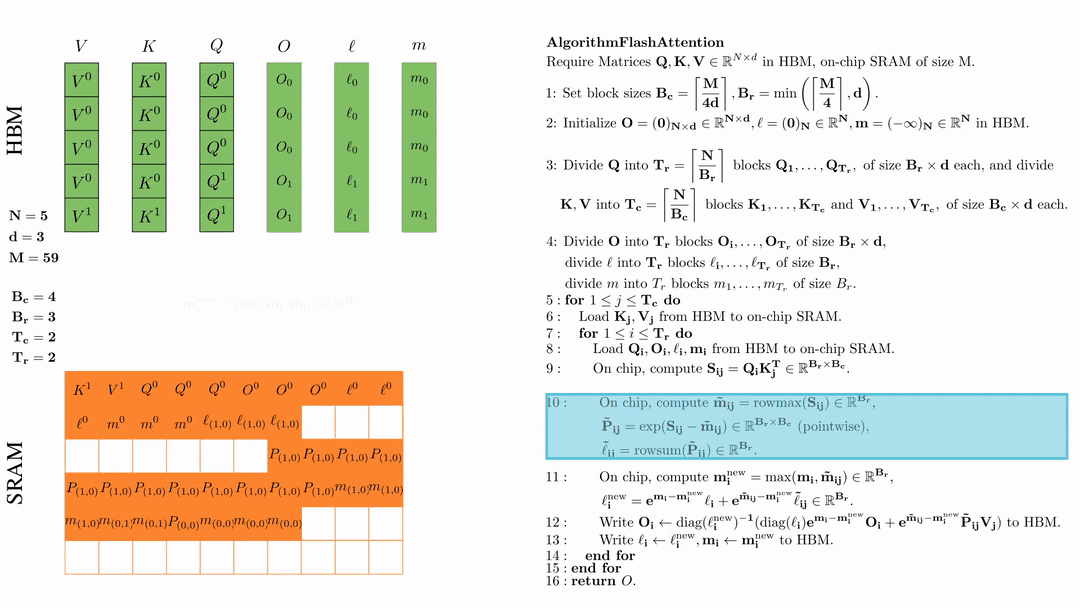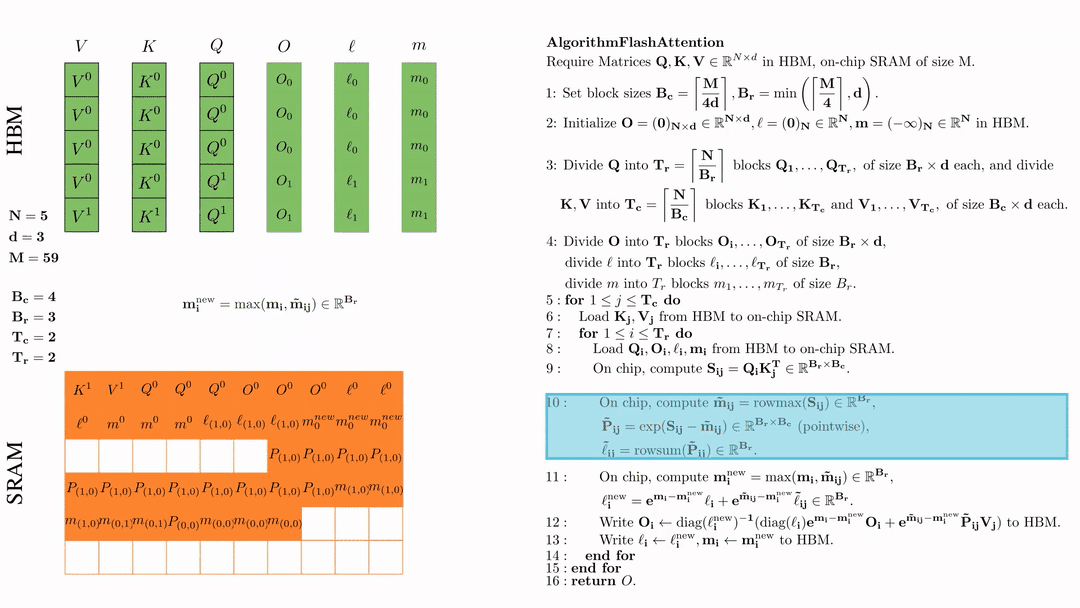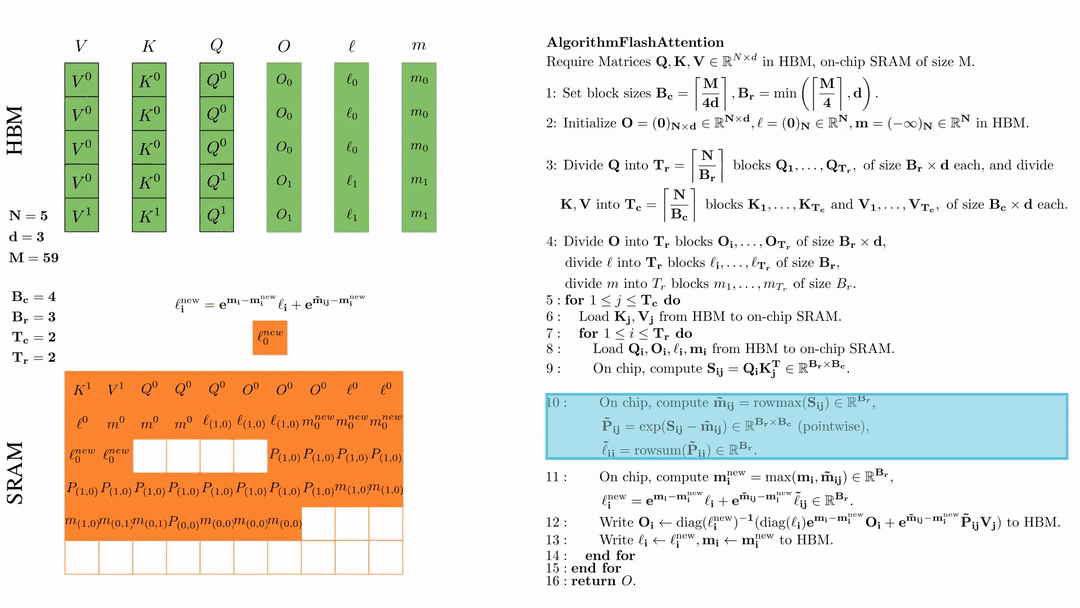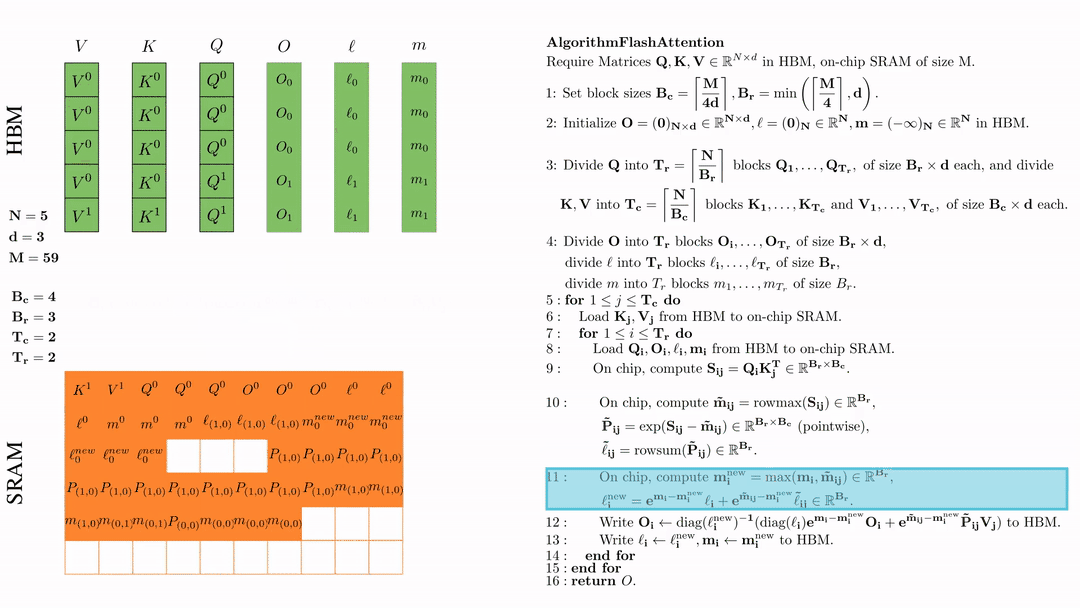
在芯片中,计算 \( \tilde{\mathbf{m}}_{ij} = \text{rowmax}(S_{ij}) \in \mathbb{R}^{B_r} \), \( \tilde{\mathbf{P}}_{ij} = \exp(S_{ij} - \tilde{\mathbf{m}}_{ij}) \in \mathbb{R}^{B_r \times B_c} \ (\text{pointwise}) \), \( \tilde{\ell}_{ij} = \text{rowsum}(\tilde{\mathbf{P}}_{ij}) \in \mathbb{R}^{B_r} \). 
在芯片中,计算 $\mathbf{m}_i^{\text{new}} = \max(\mathbf{m}_i, \tilde{\mathbf{m}}_{ij}) \in \mathbb{R}^{B_r}$, $\ell_i^{\text{new}} = e^{\mathbf{m}_i - \mathbf{m}_i^{\text{new}}} \ell_i + e^{\tilde{\mathbf{m}}_{ij} - \mathbf{m}_i^{\text{new}}} \tilde{\ell}_{ij} \in \mathbb{R}^{B_r}.$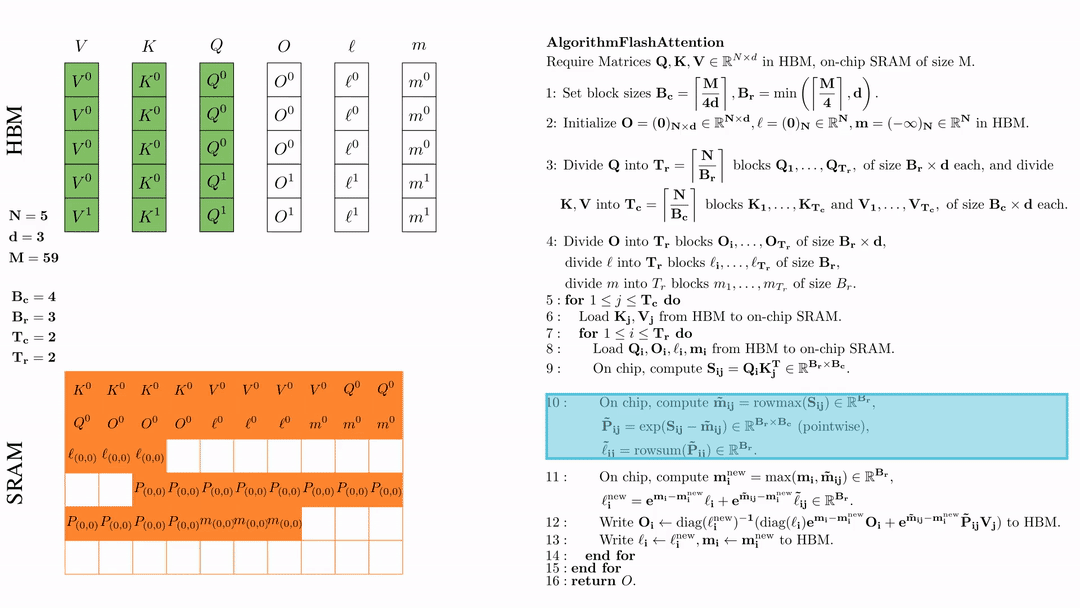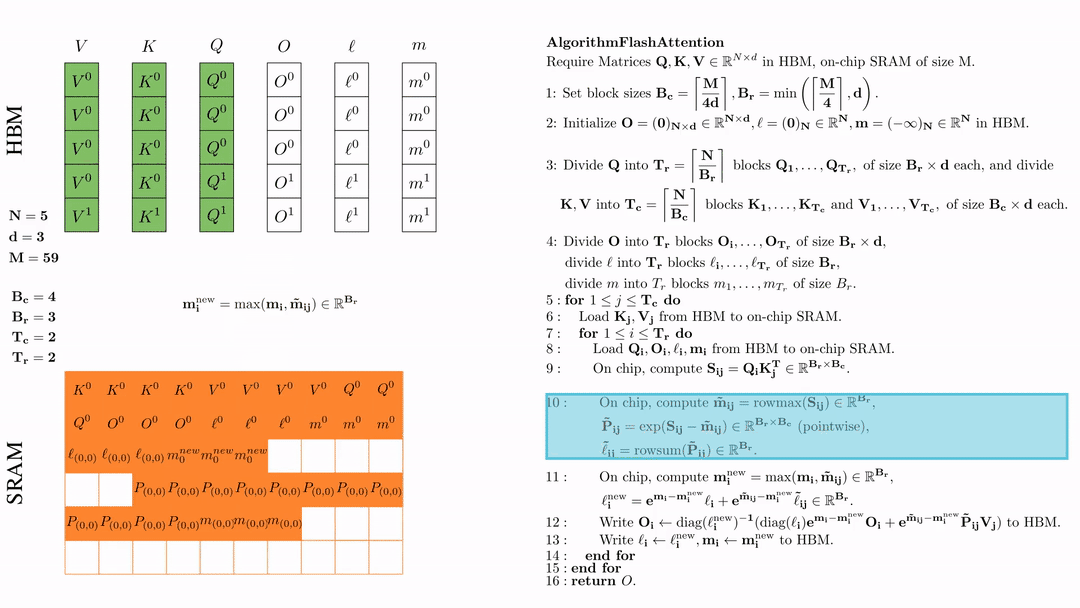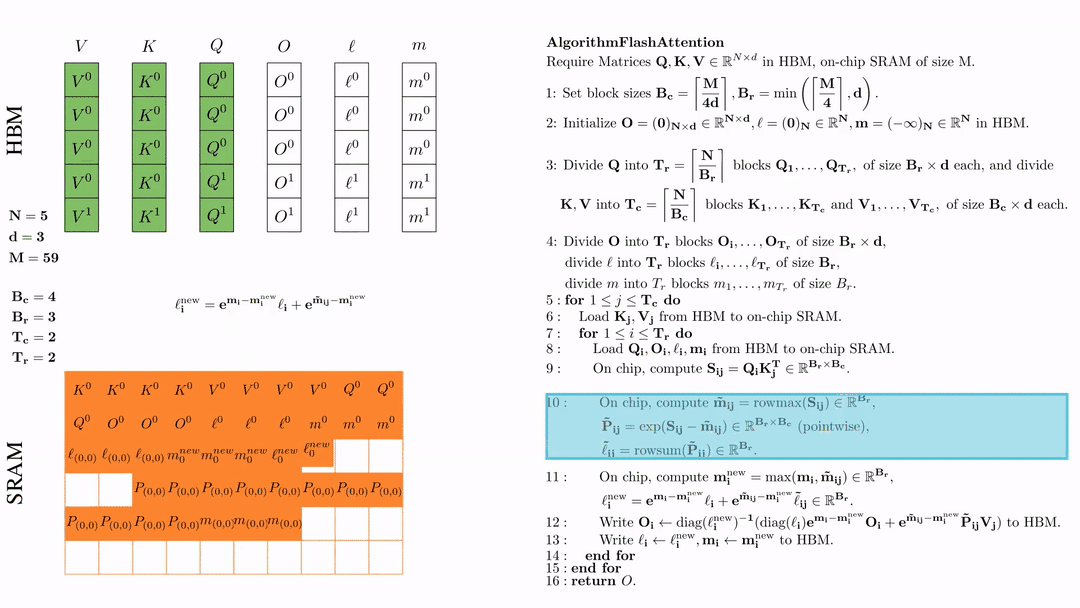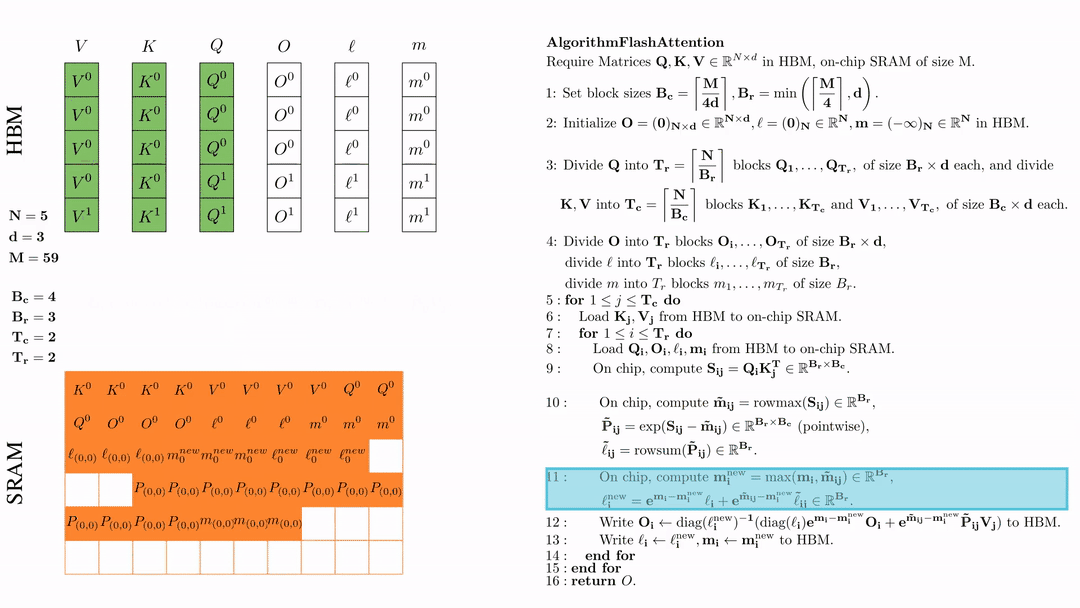
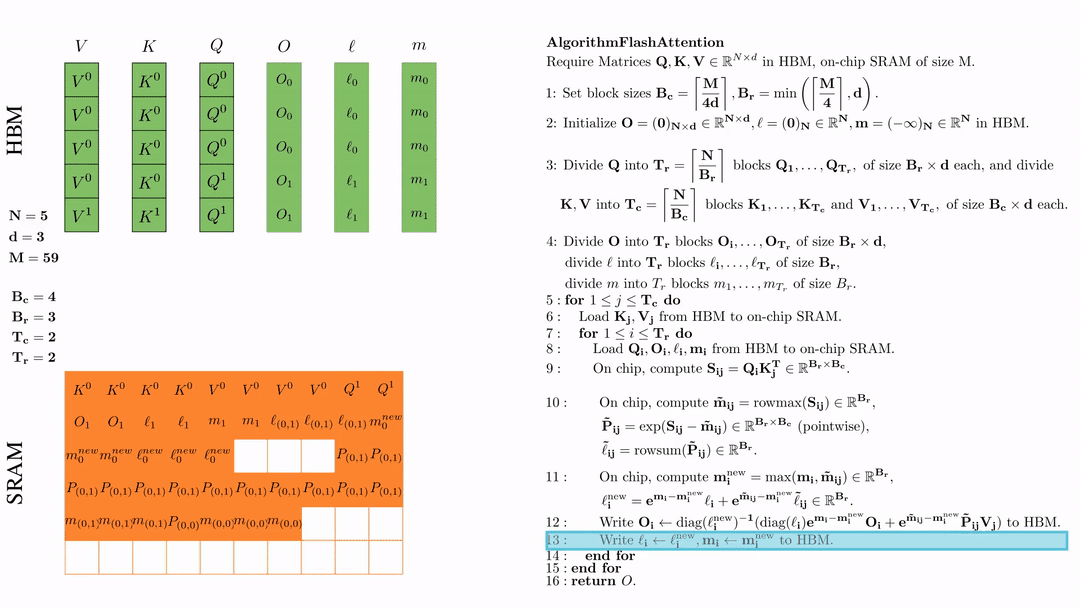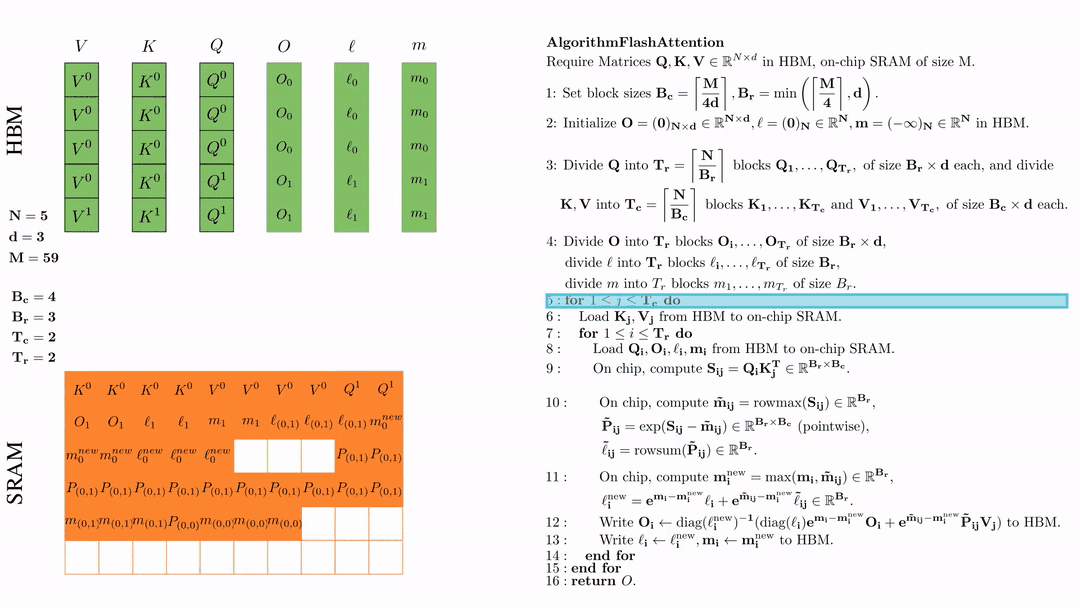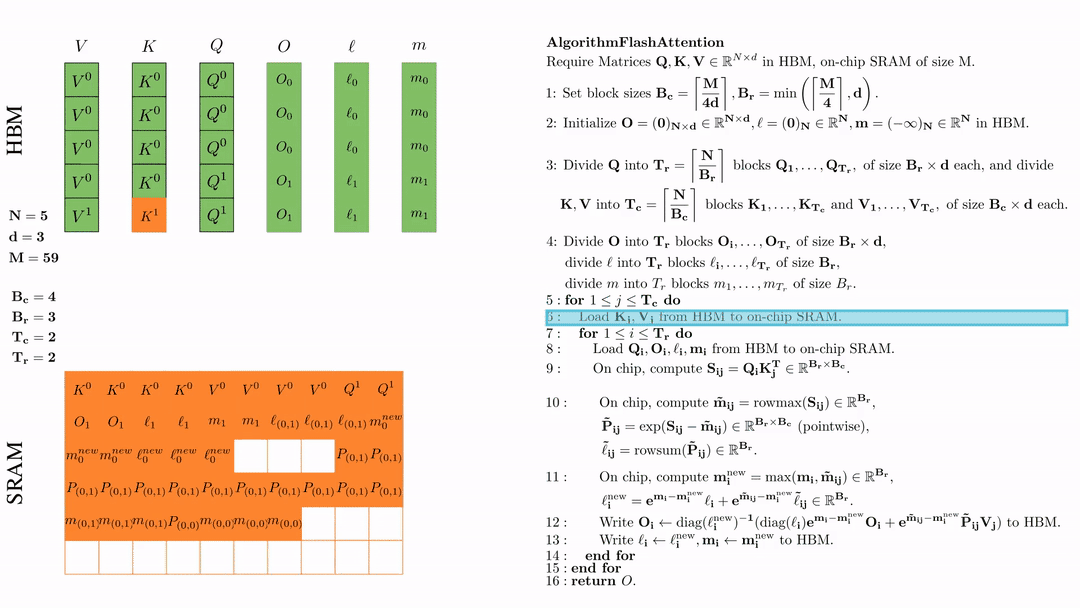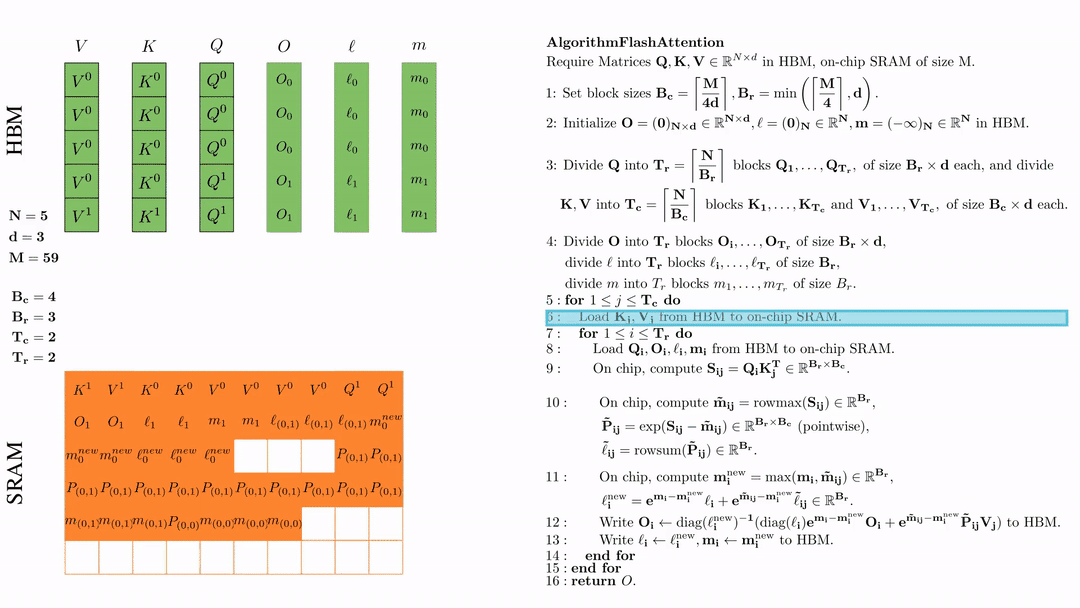
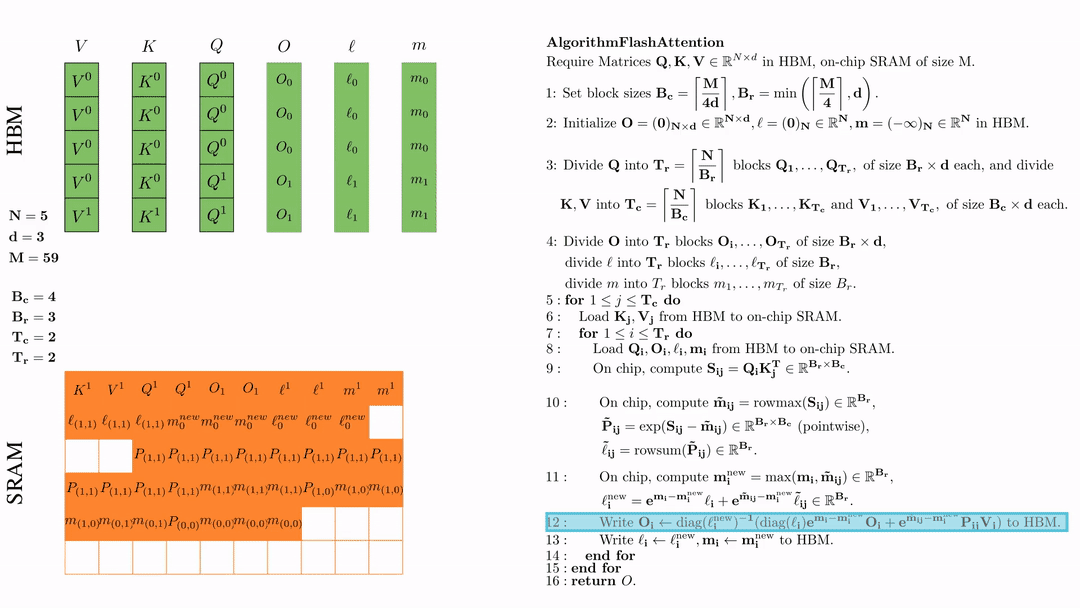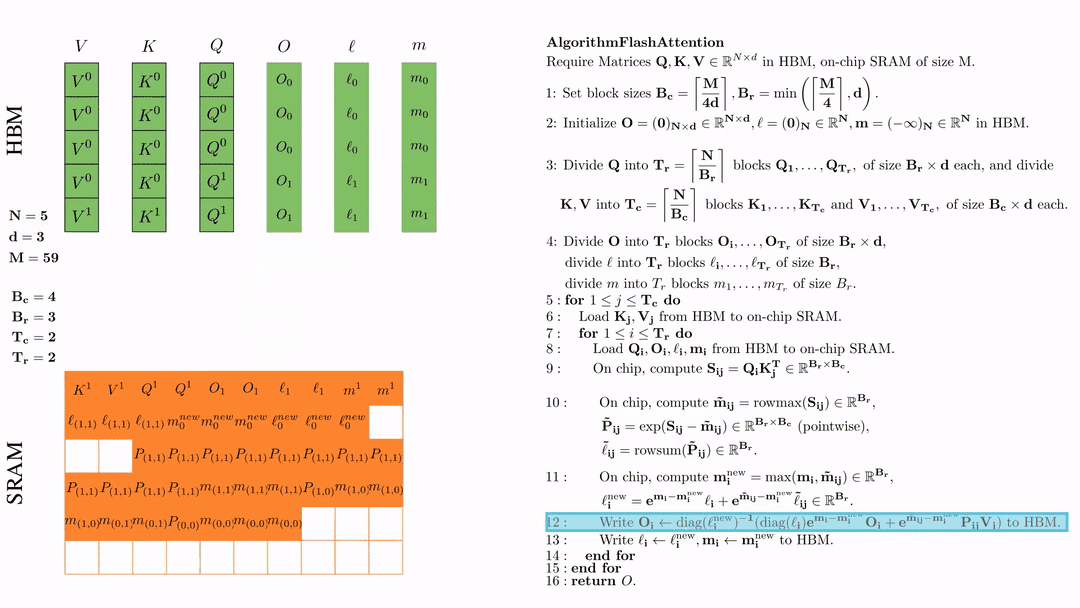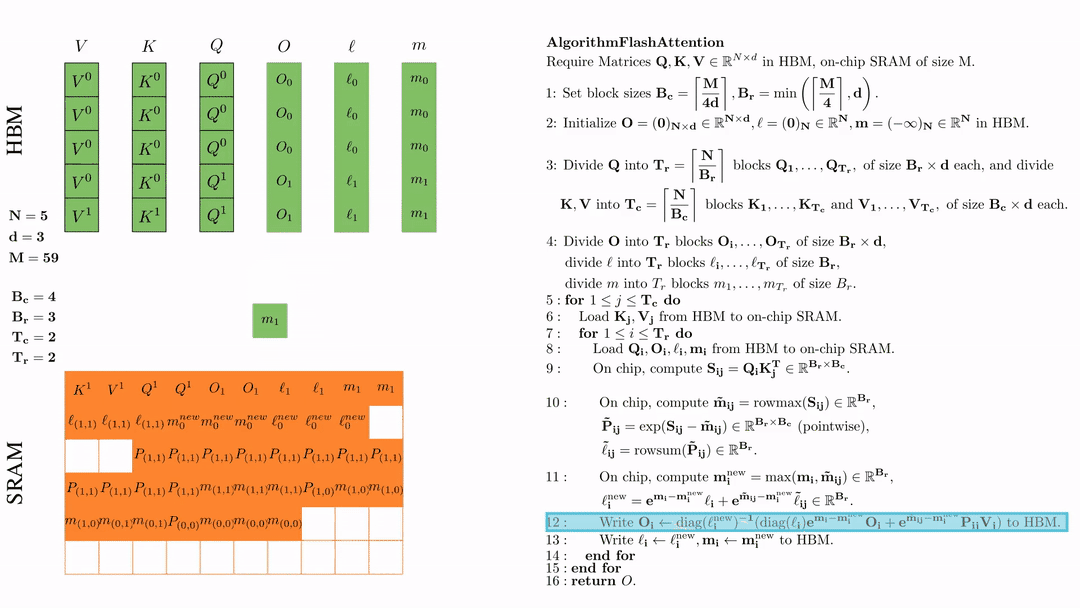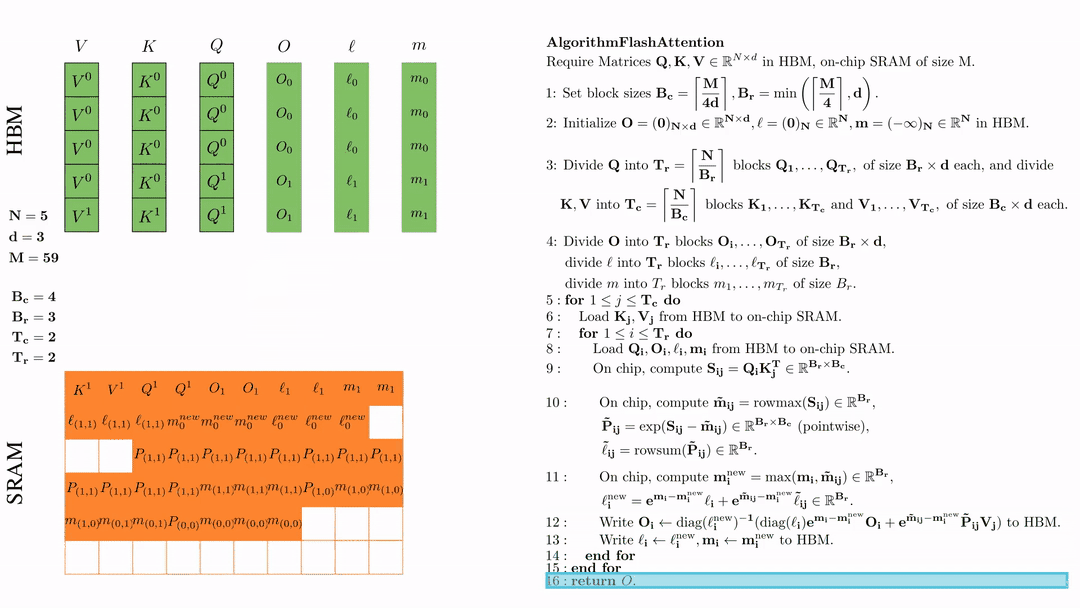
将\( O_i \)更新后写入到HBM,$O_i \leftarrow \text{diag}(l_i^{\text{new}})^{-1} \big( \text{diag}(\ell_i) e^{\mathbf{m}_i - \mathbf{m}_i^{\text{new}}} O_i + e^{\tilde{\mathbf{m}}_{ij} - \mathbf{m}_i^{\text{new}}} \tilde{\mathbf{P}}_{ij} V_j \big)$。
这是最复杂的一步。我们首先来看diag(l),这里l是一个向量。用diag(l)×N 的作用就是用l的每一个元素乘以N的对应列。说起来有些抽象,我们来看一个例子:
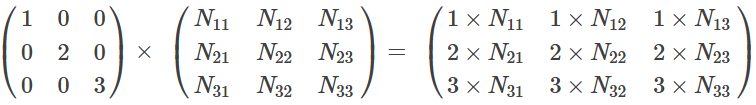
为什么要搞出这么复杂的东西呢?目的就是把前面我们更新l的公式能写成矩阵乘法的形式,这样才能在GPU上高效计算。
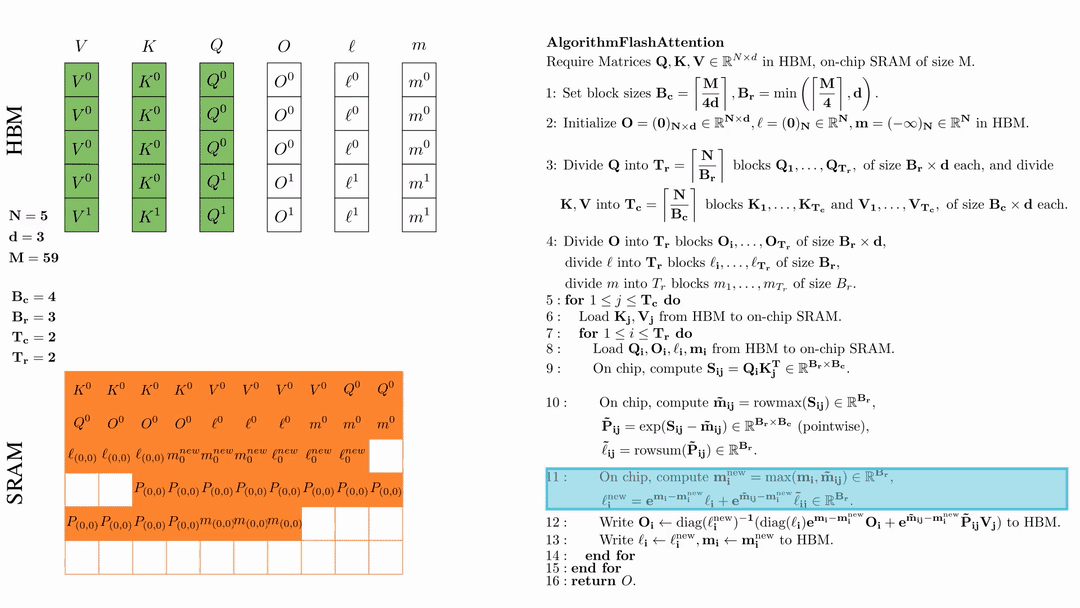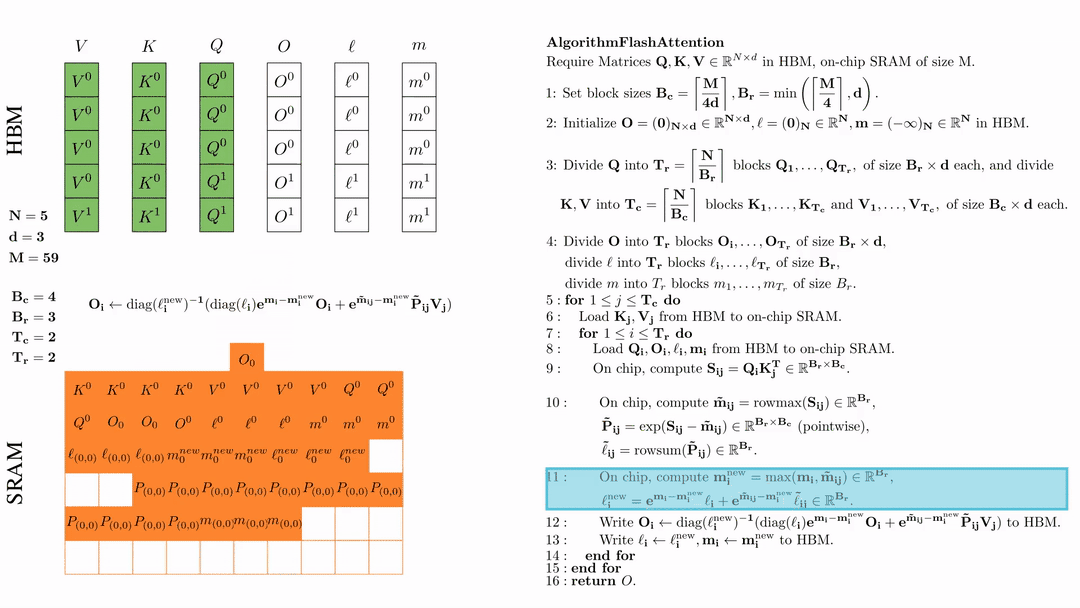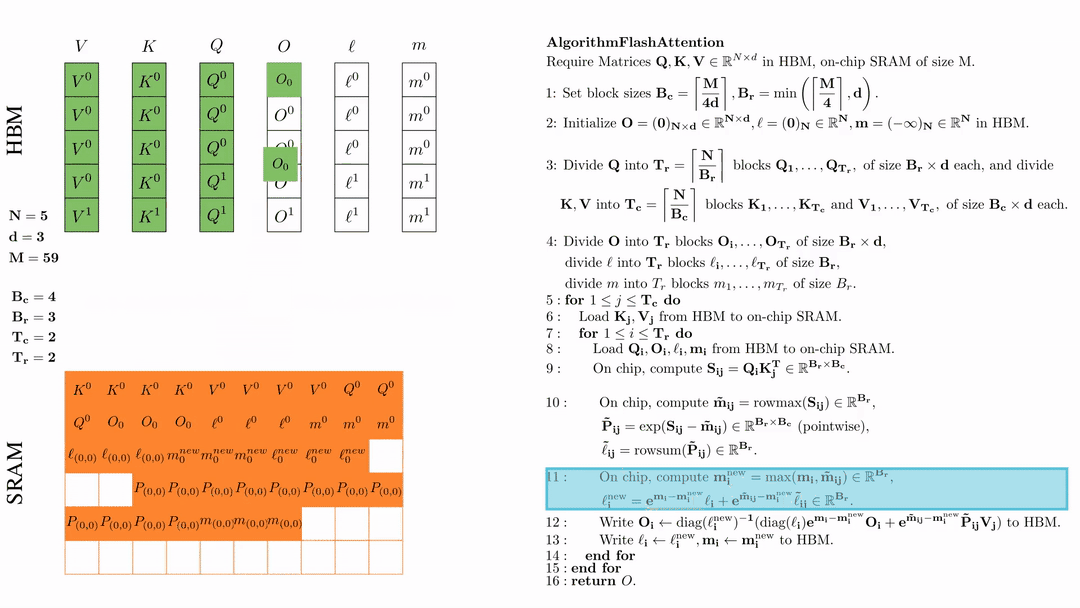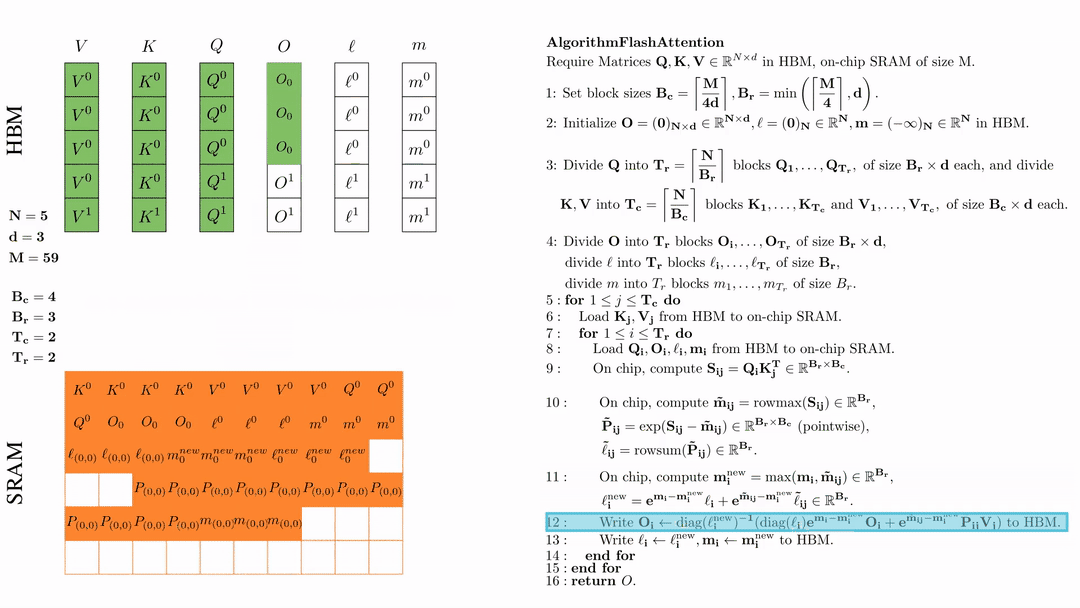
将\( l_i, m_i \)更新后写入HBM,$\ell_i \leftarrow \ell_i^{\text{new}}, \mathbf{m}_i \leftarrow \mathbf{m}_i^{\text{new}}$。
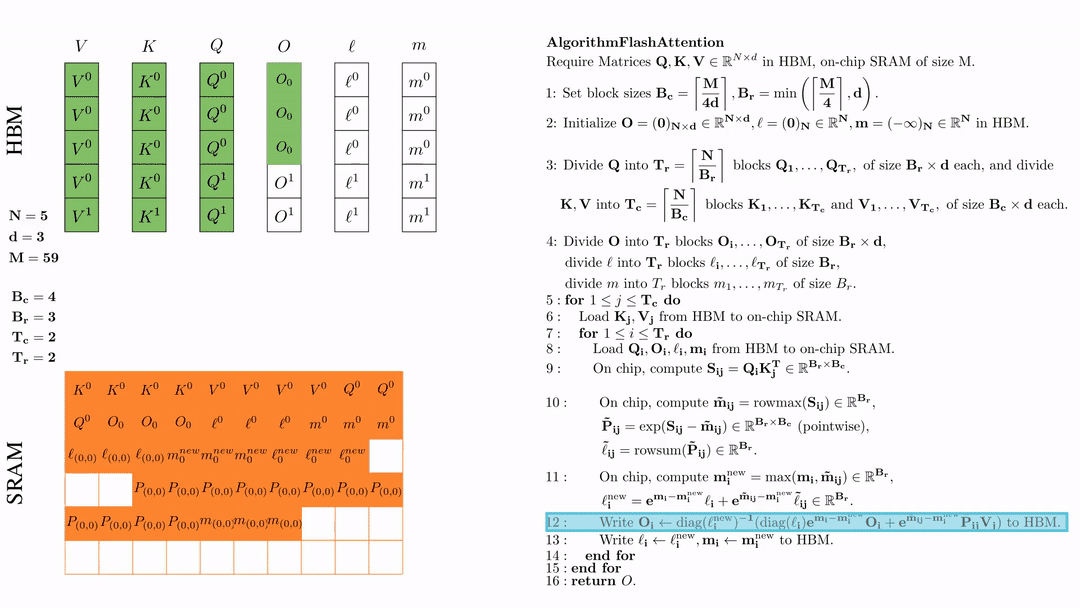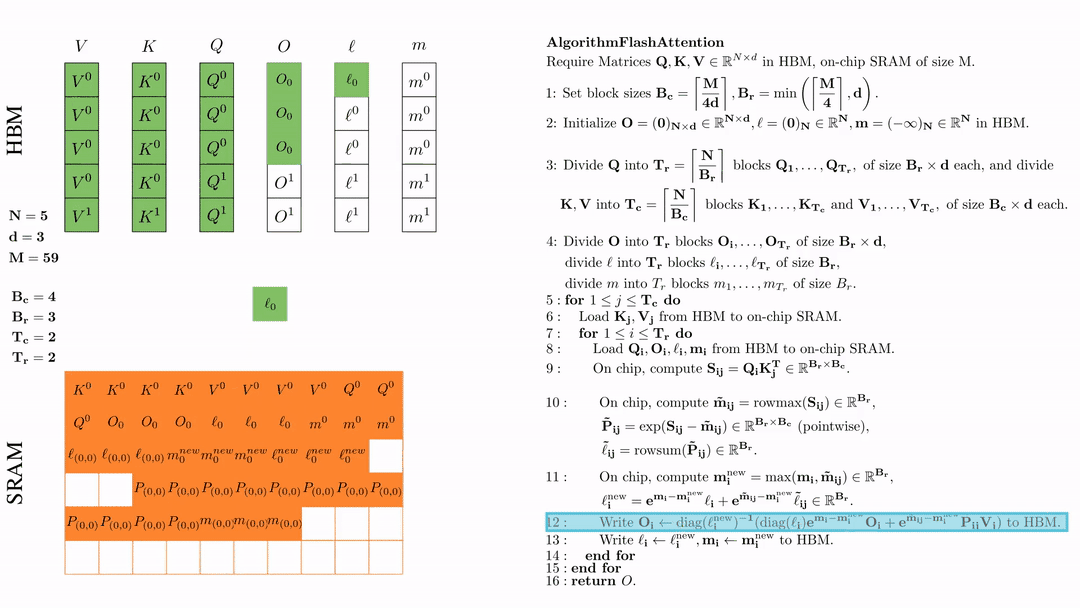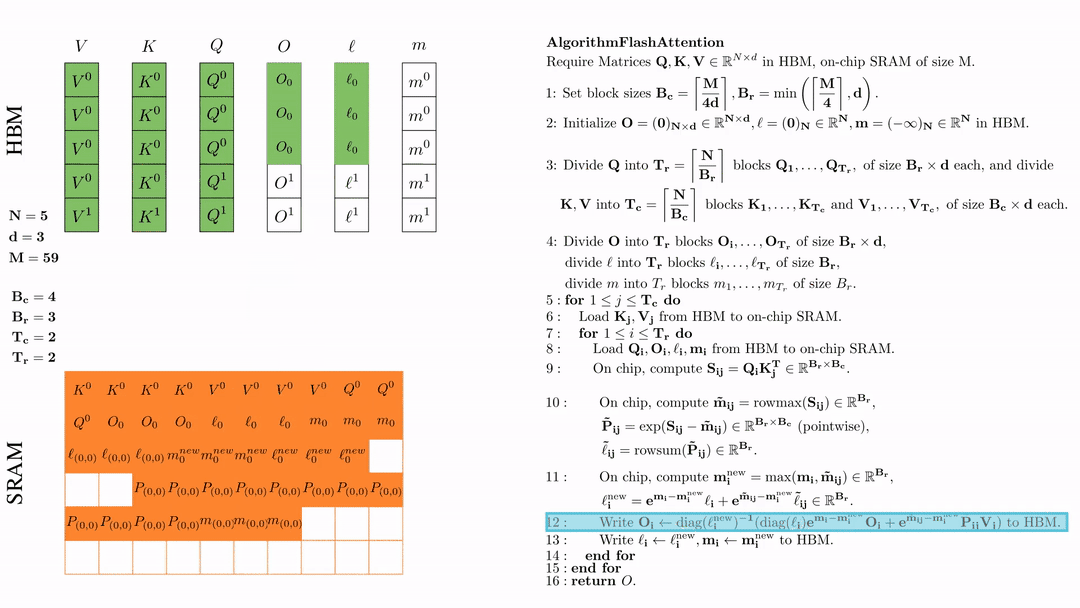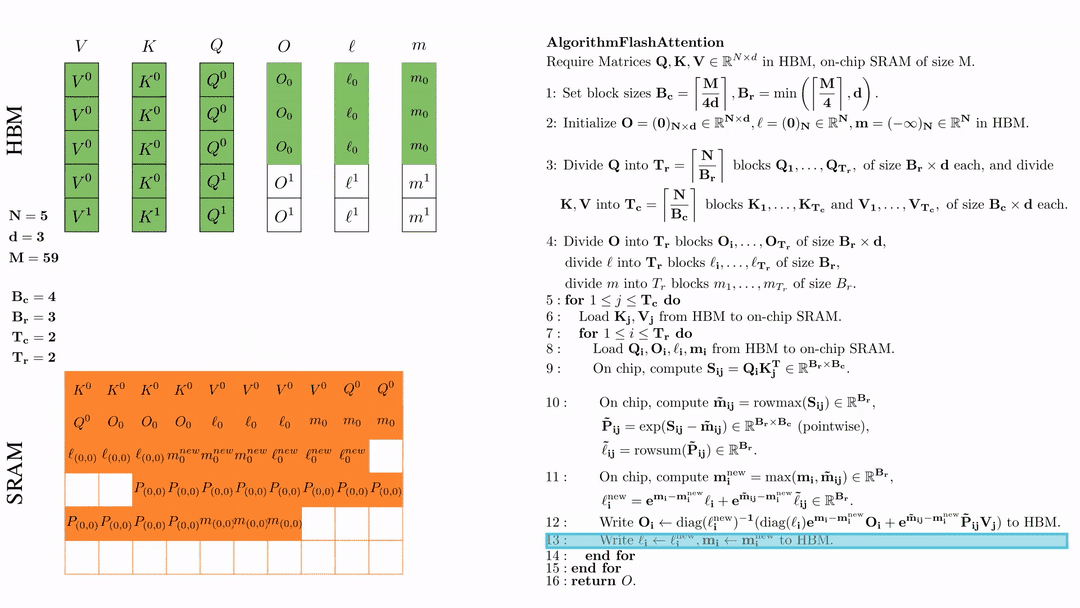
第二次内层循环 \(\text{for } 1 \leq j \leq T_r \text{ do } \) 将\( Q_i, O_i, l_i, m_i \)从HDM加载到SRAM。
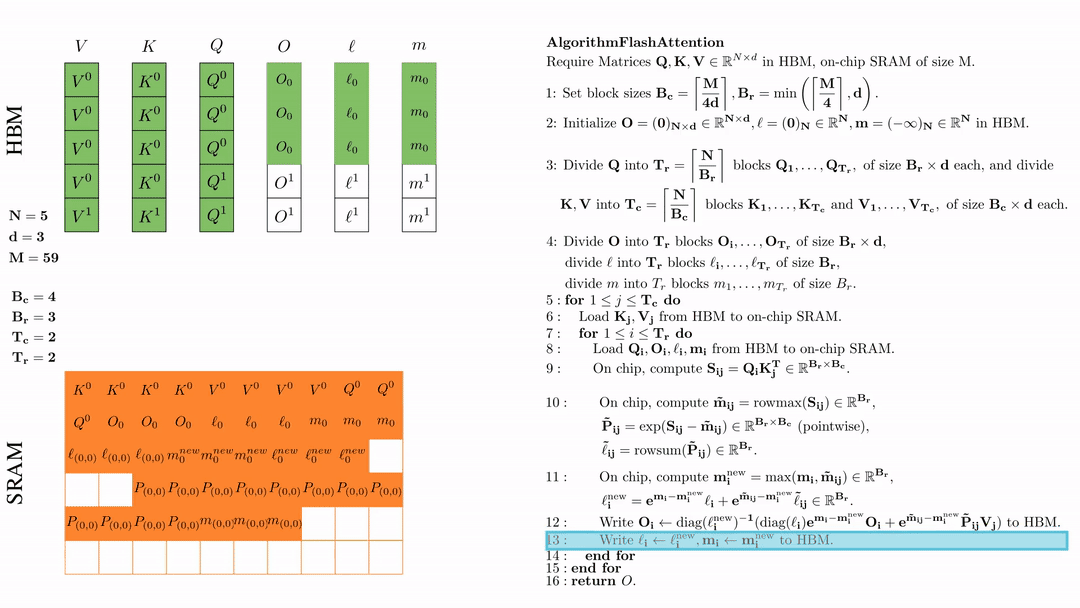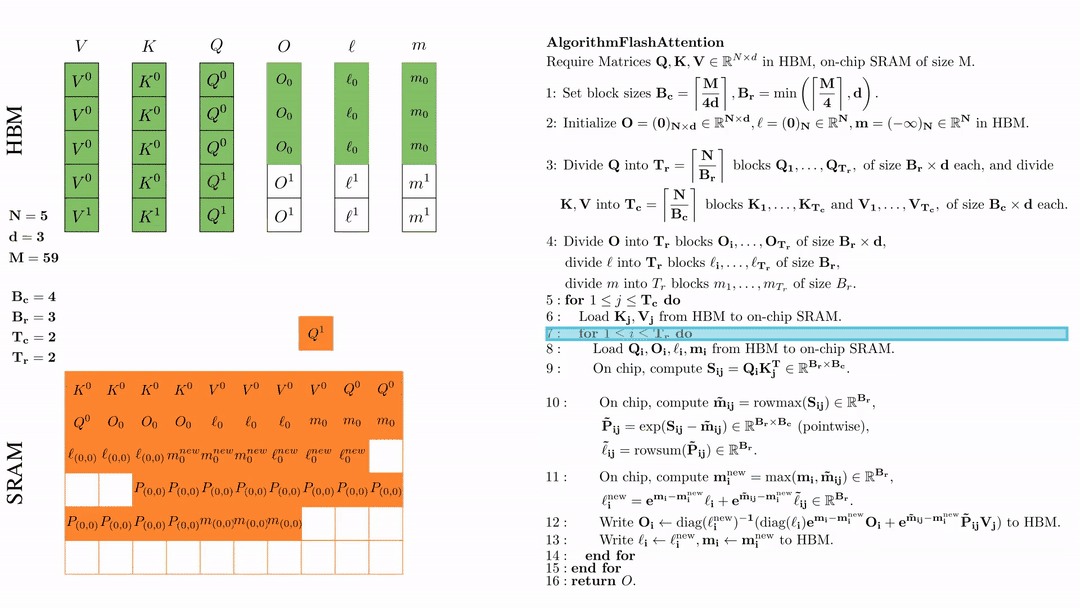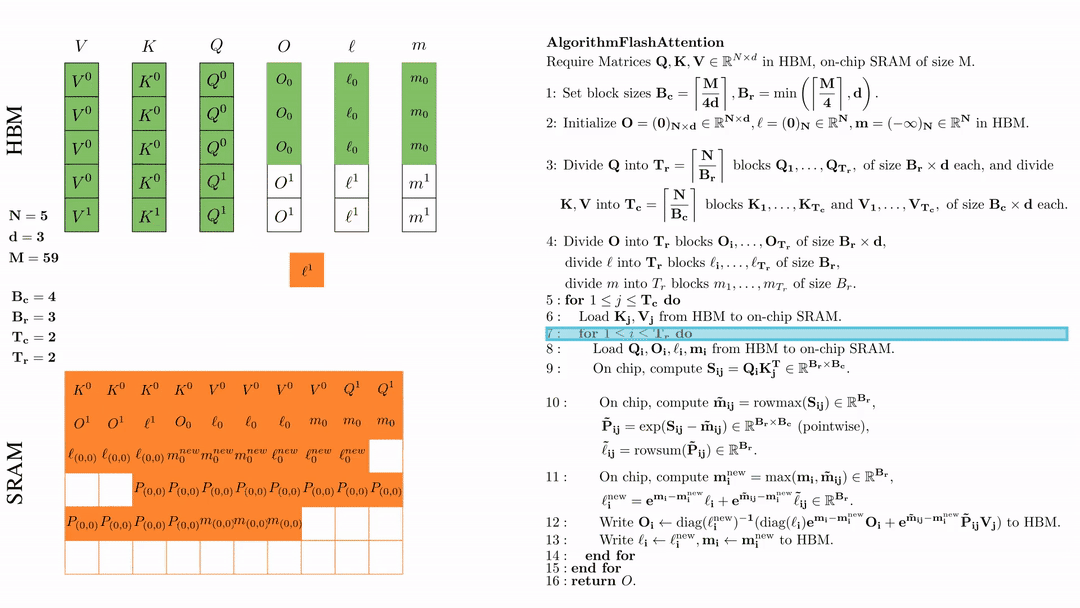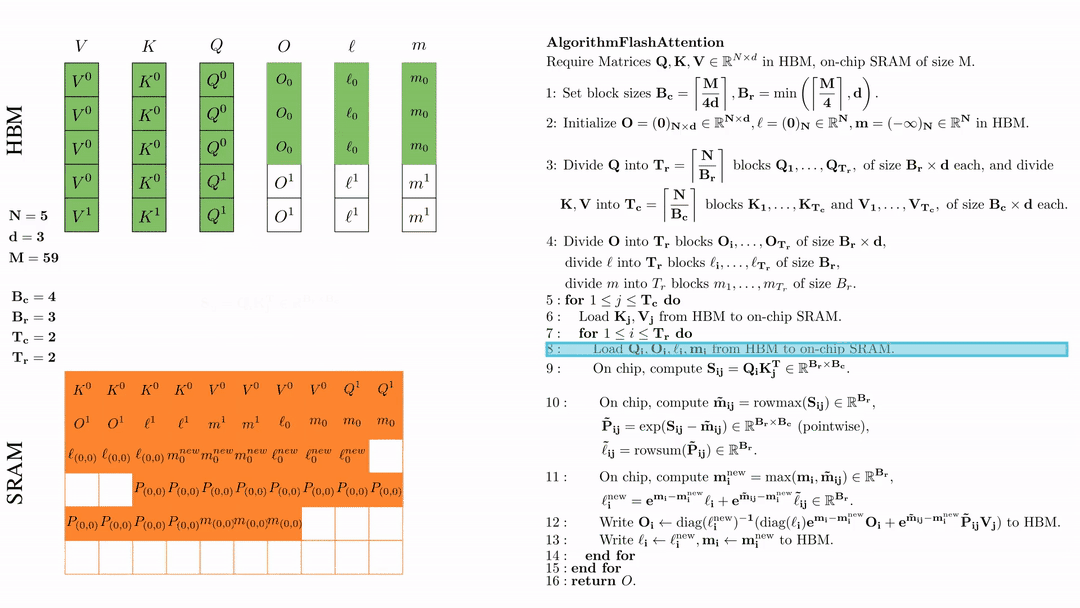
在芯片中,计算\( S_{ij} = Q_i K_j^{\text{T}} \in \mathbb{R}^{B_r \times B_c} \)
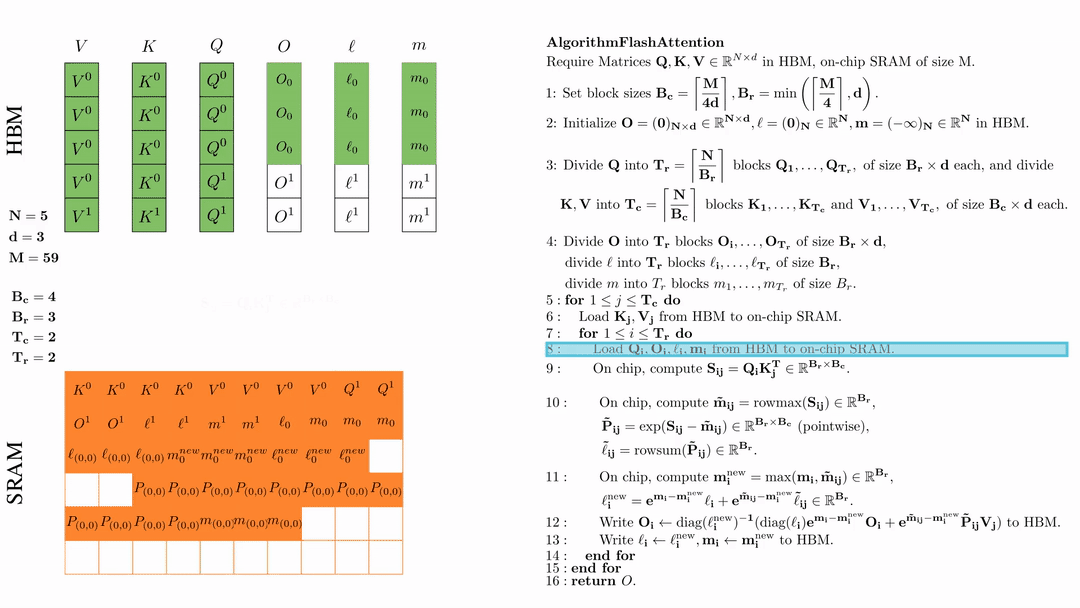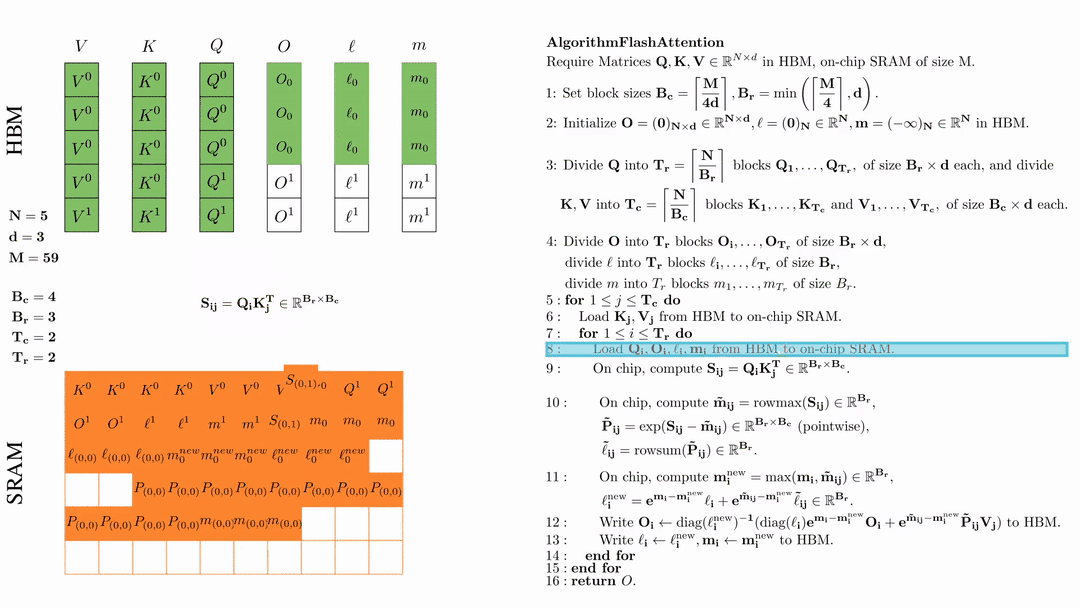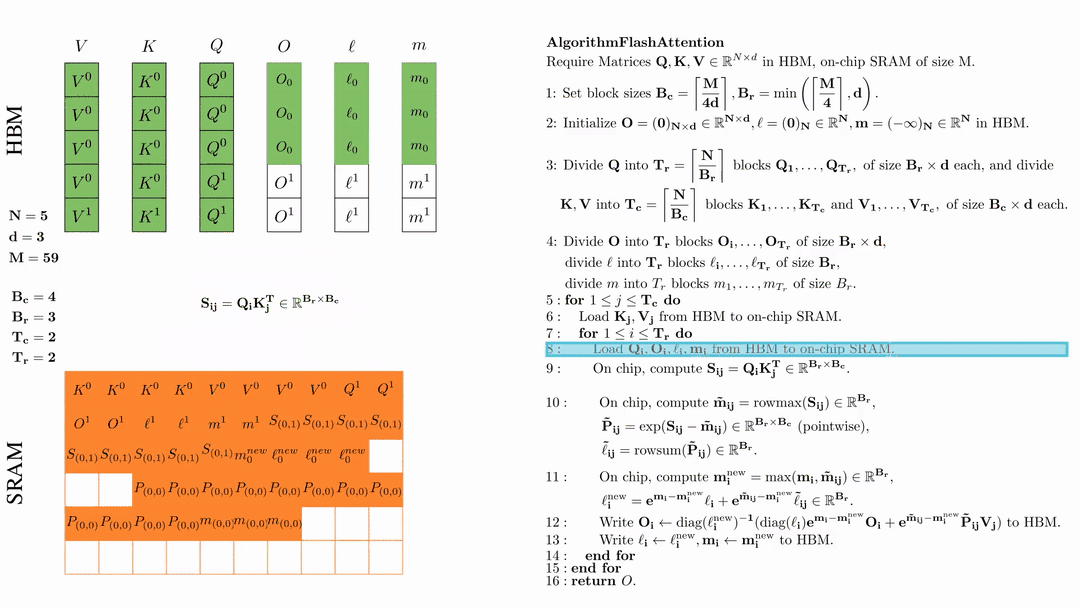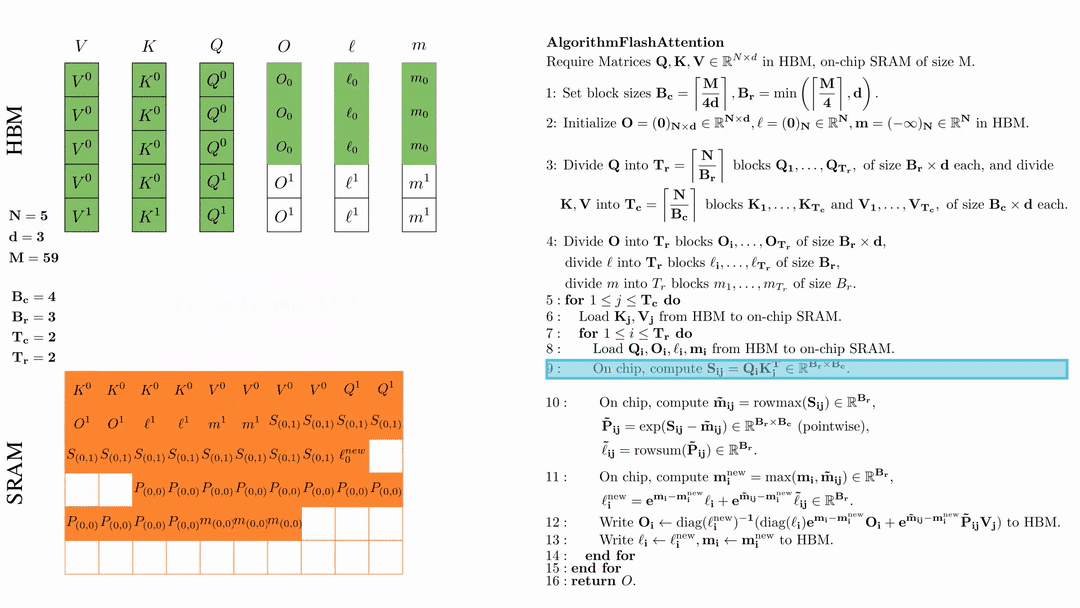
在芯片中,计算 \( \tilde{\mathbf{m}}_{ij} = \text{rowmax}(S_{ij}) \in \mathbb{R}^{B_r} \), \( \tilde{\mathbf{P}}_{ij} = \exp(S_{ij} - \tilde{\mathbf{m}}_{ij}) \in \mathbb{R}^{B_r \times B_c} \ (\text{pointwise}) \), \( \tilde{\ell}_{ij} = \text{rowsum}(\tilde{\mathbf{P}}_{ij}) \in \mathbb{R}^{B_r} \).
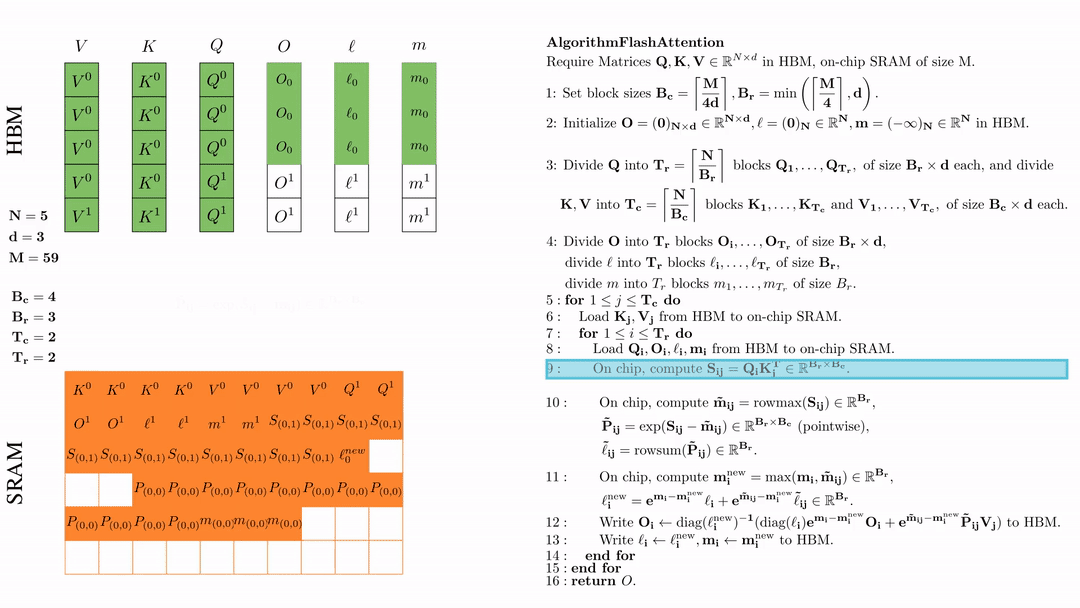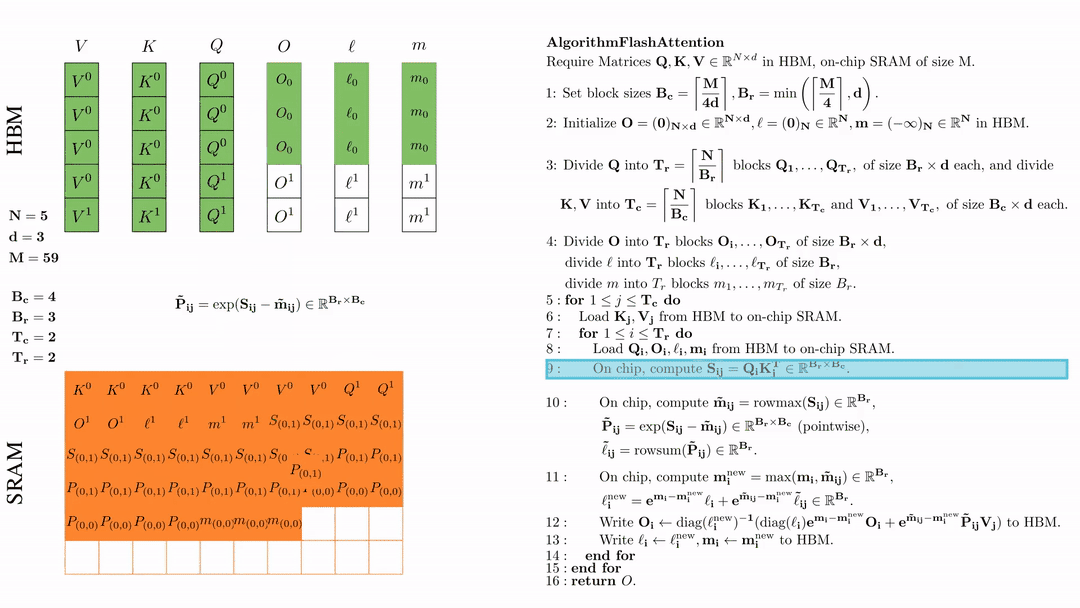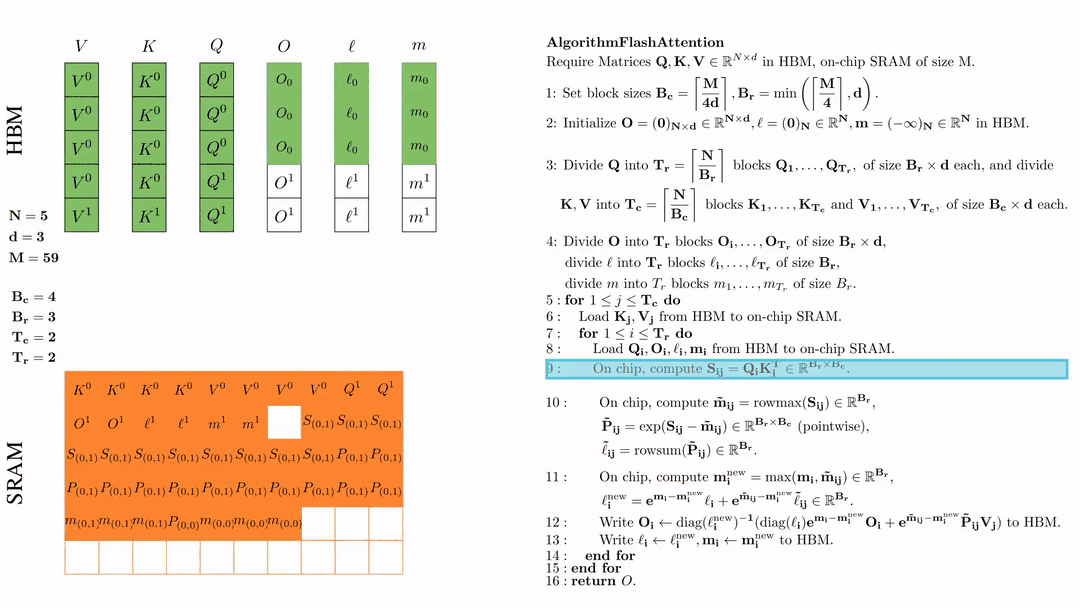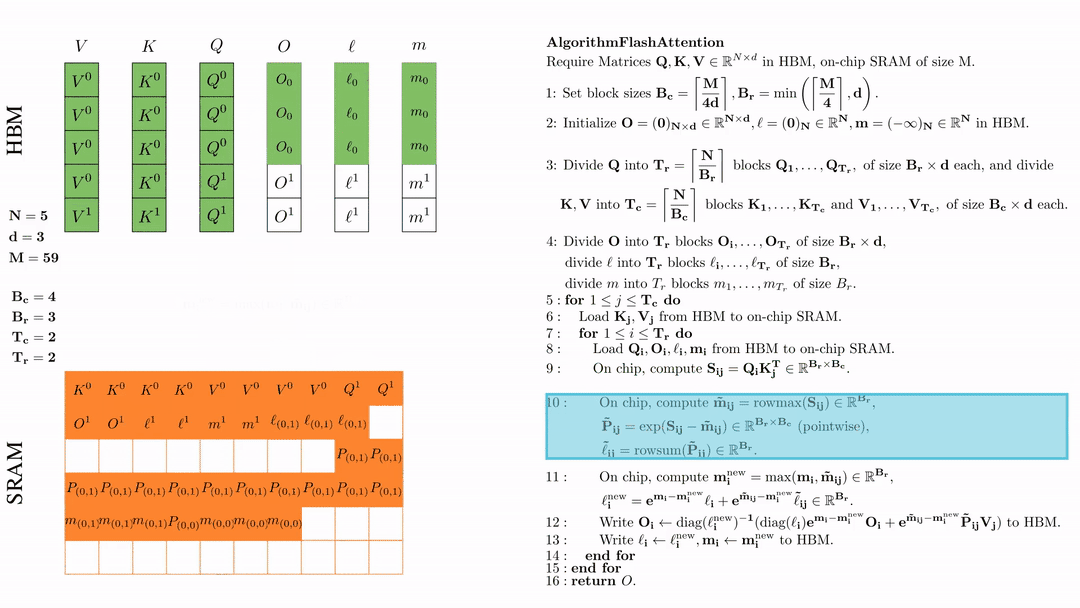
在芯片中,计算 $\mathbf{m}_i^{\text{new}} = \max(\mathbf{m}_i, \tilde{\mathbf{m}}_{ij}) \in \mathbb{R}^{B_r}$, $\ell_i^{\text{new}} = e^{\mathbf{m}_i - \mathbf{m}_i^{\text{new}}} \ell_i + e^{\tilde{\mathbf{m}}_{ij} - \mathbf{m}_i^{\text{new}}} \tilde{\ell}_{ij} \in \mathbb{R}^{B_r}.$
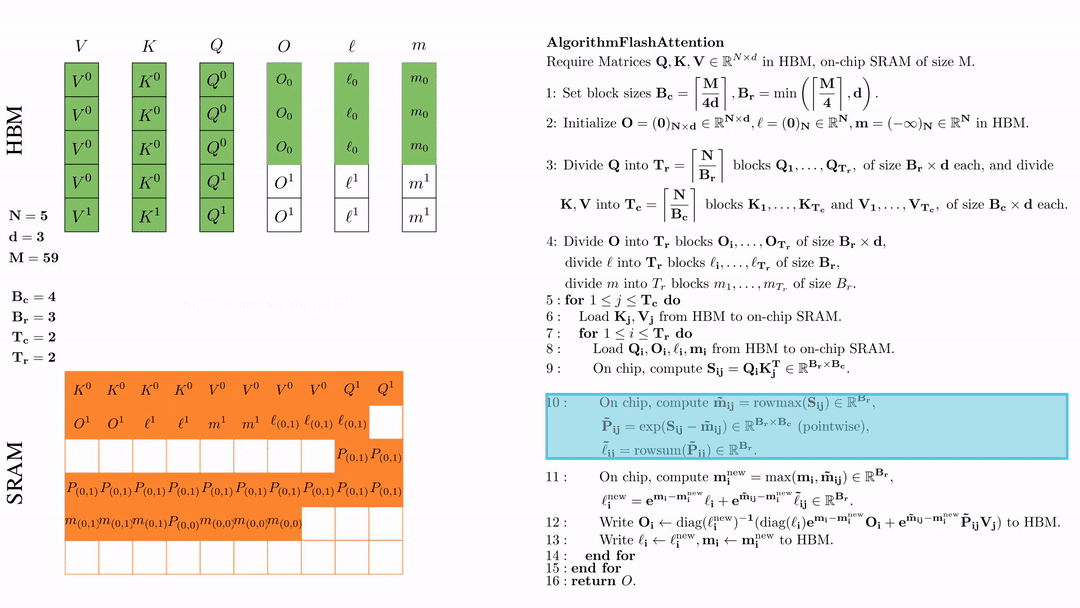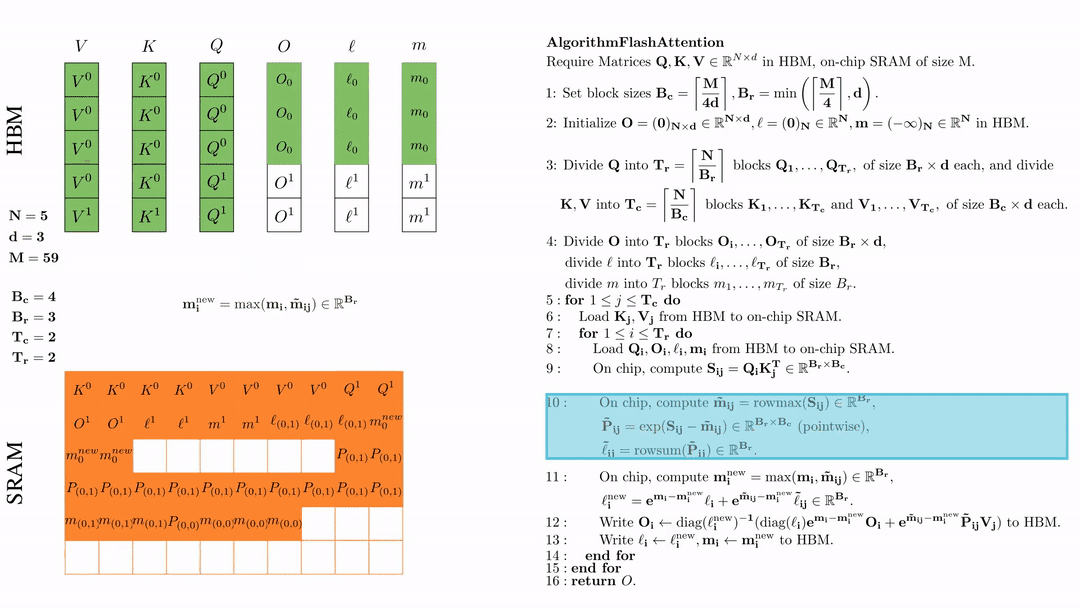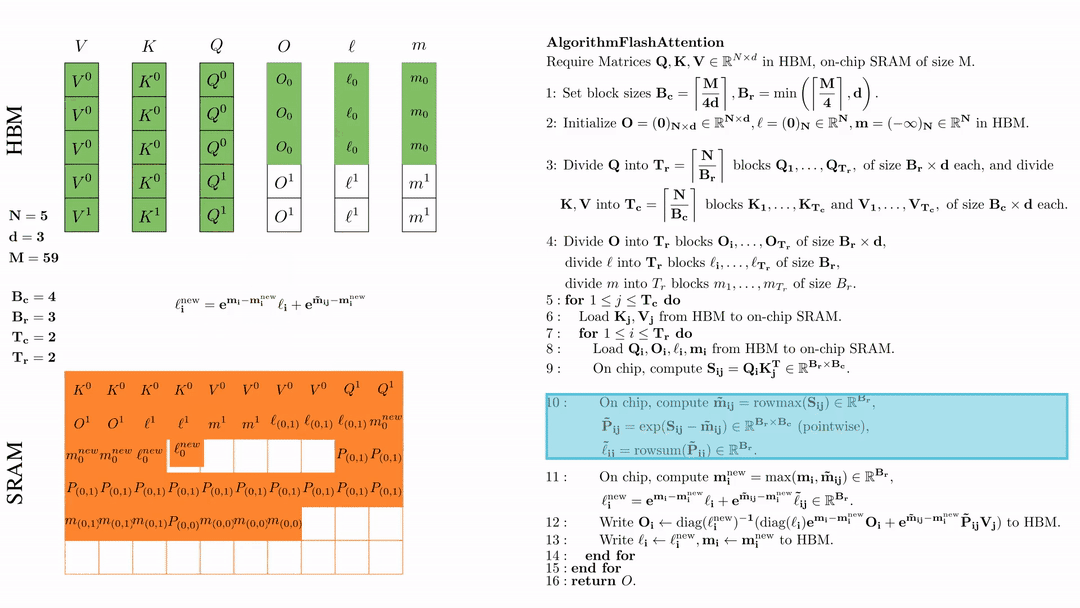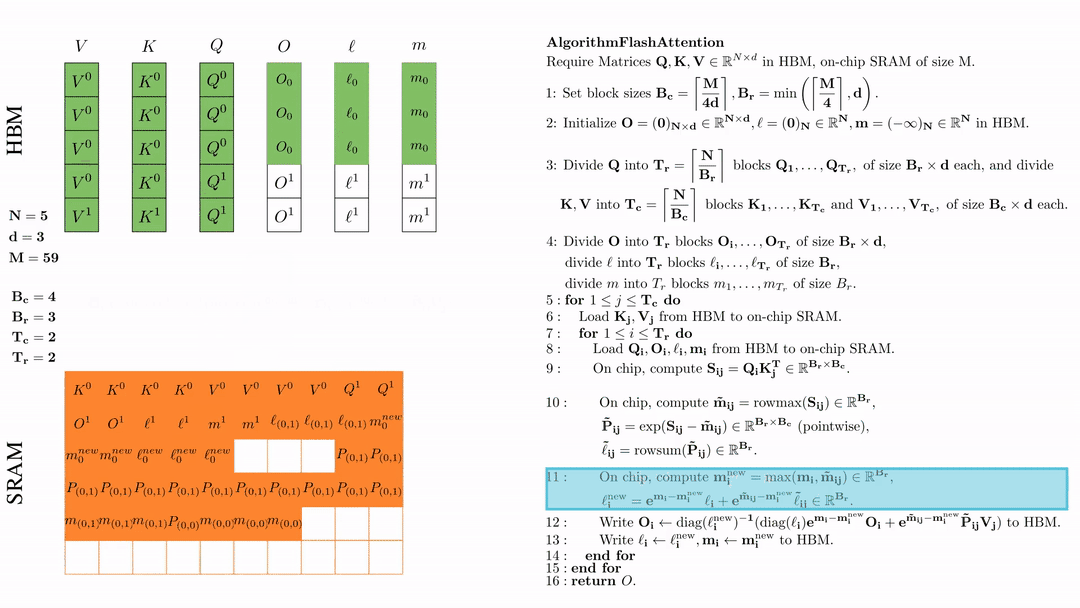
将\( O_i \)更新后写入到HBM,$O_i \leftarrow \text{diag}(l_i^{\text{new}})^{-1} \big( \text{diag}(\ell_i) e^{\mathbf{m}_i - \mathbf{m}_i^{\text{new}}} O_i + e^{\tilde{\mathbf{m}}_{ij} - \mathbf{m}_i^{\text{new}}} \tilde{\mathbf{P}}_{ij} V_j \big)$。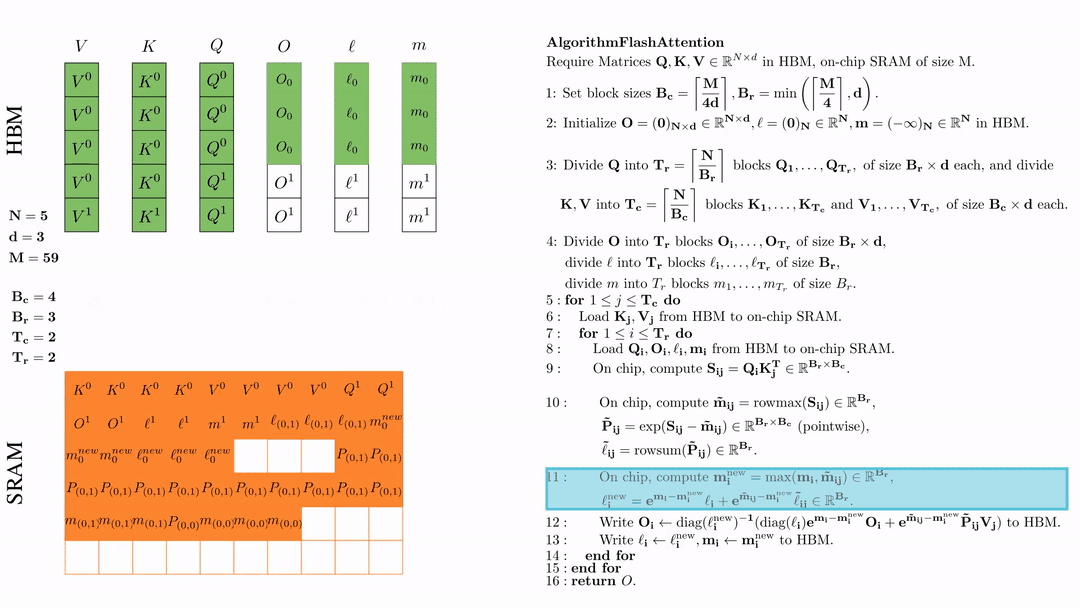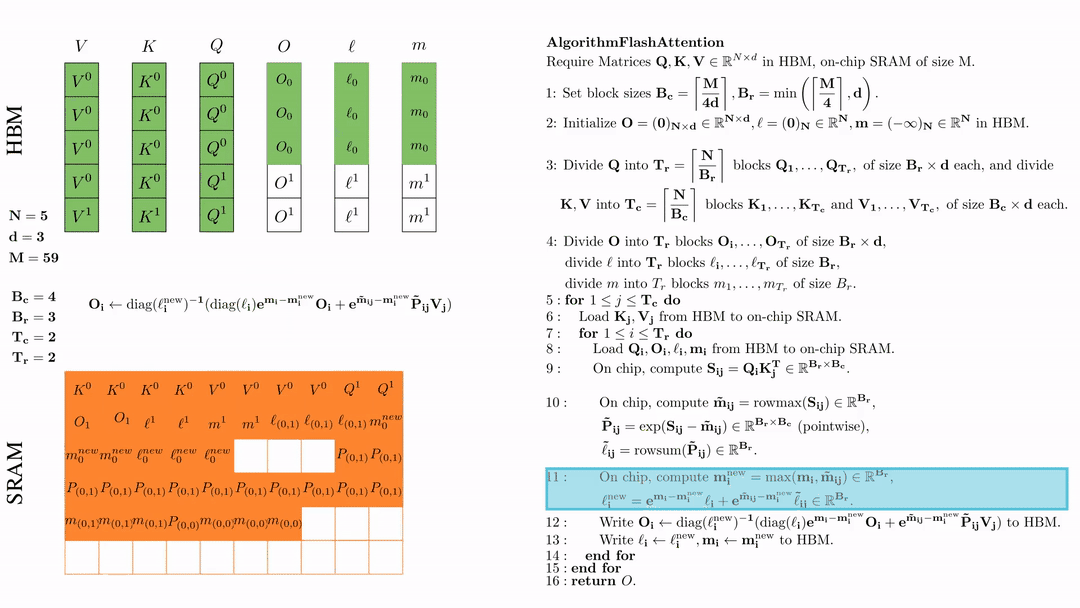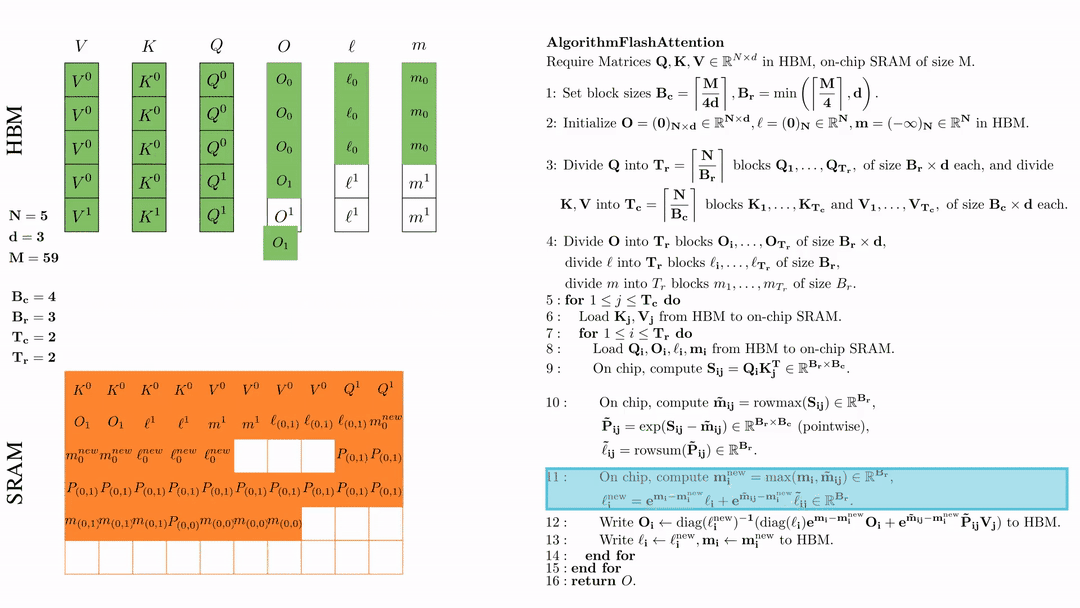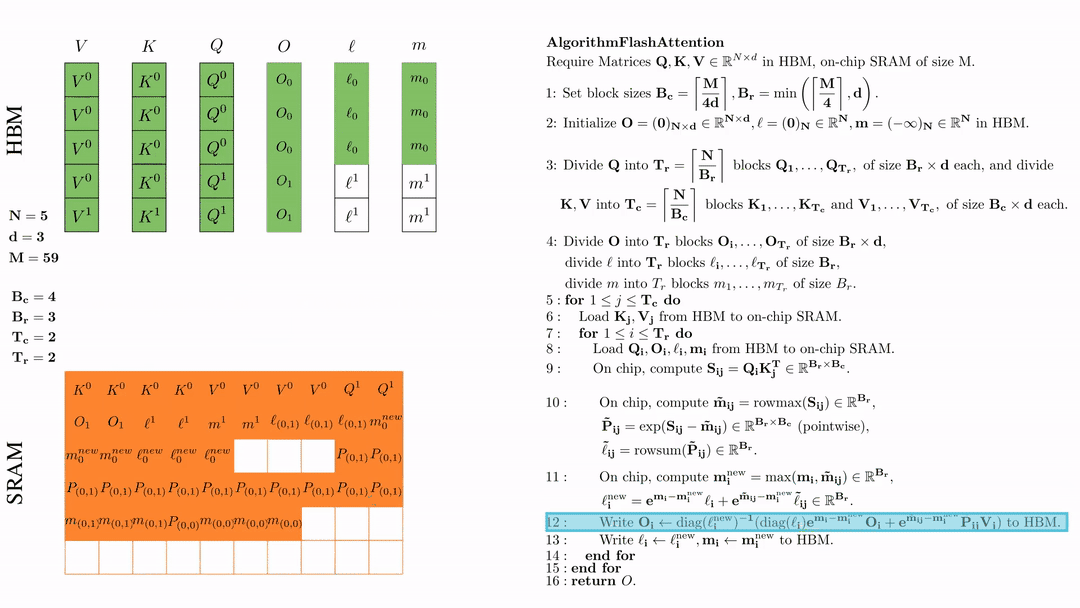
将\( l_i, m_i \)更新后写入HBM,$\ell_i \leftarrow \ell_i^{\text{new}}, \mathbf{m}_i \leftarrow \mathbf{m}_i^{\text{new}}$。
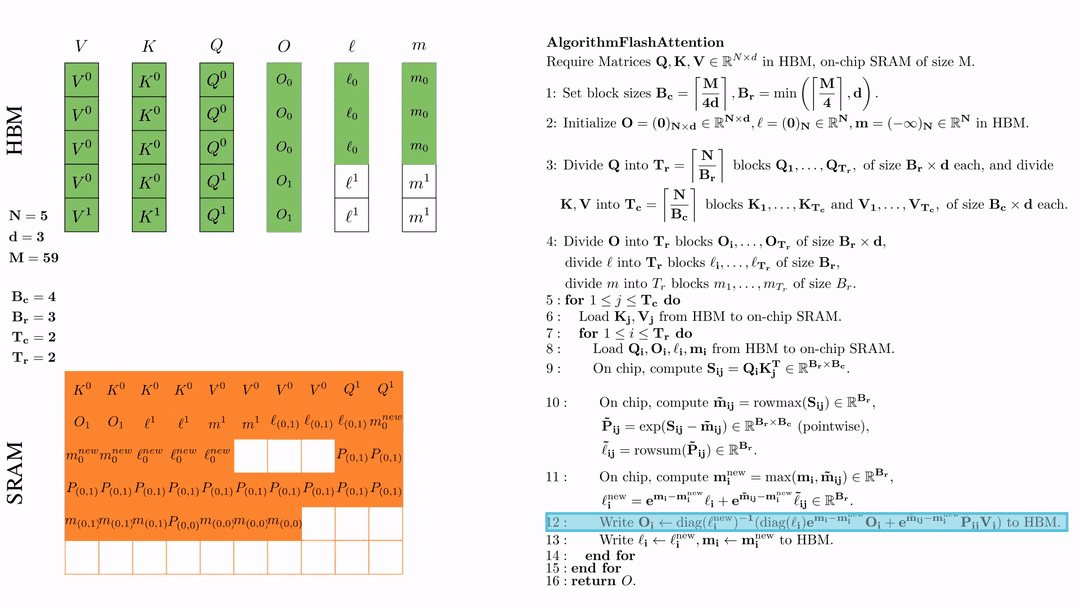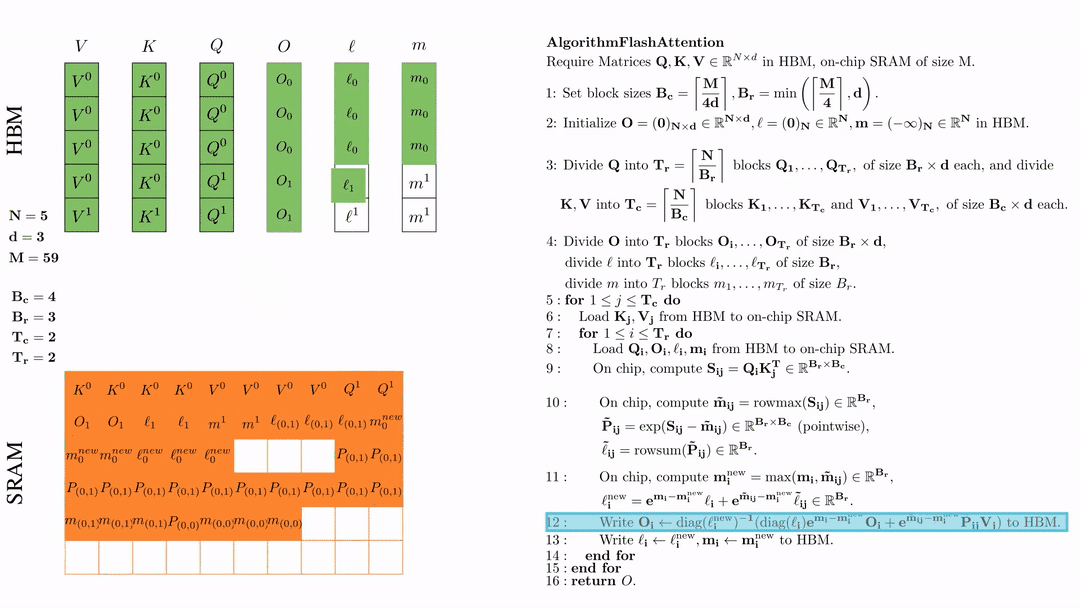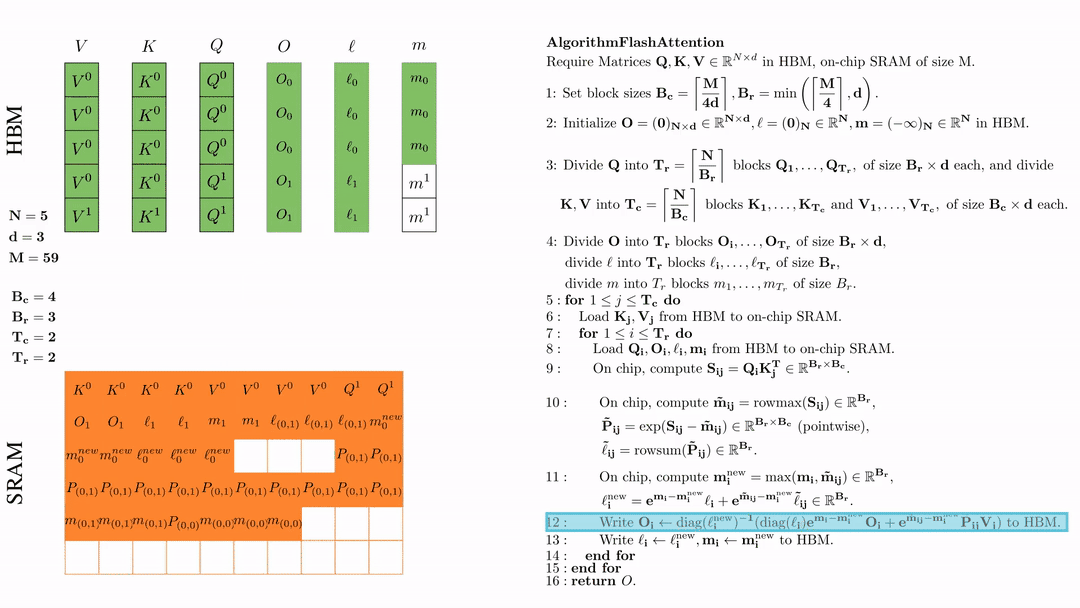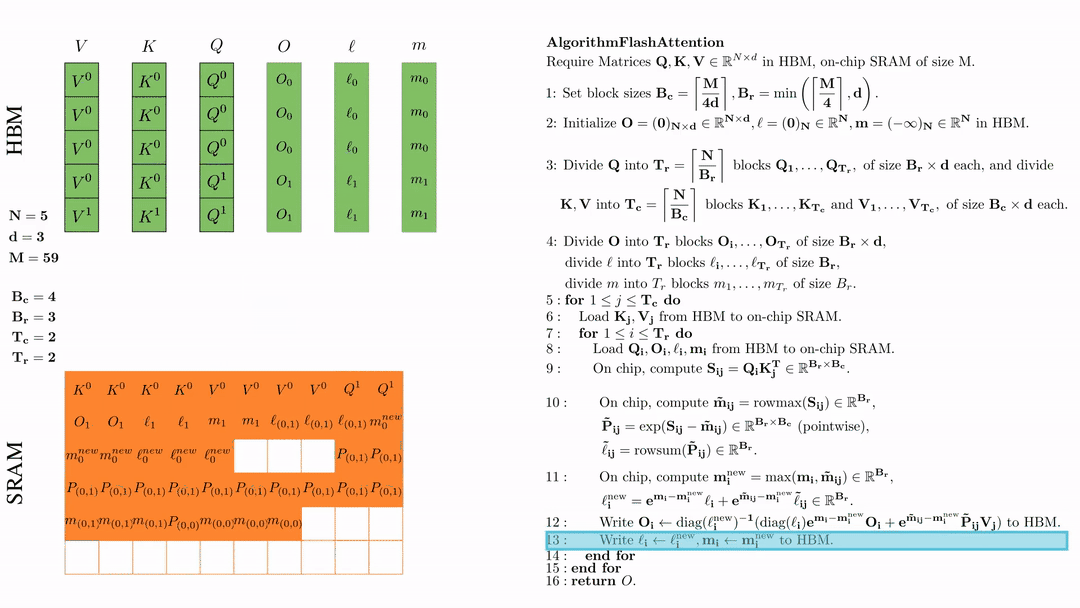
第二次外层循环 \(\text{for } 1 \leq j \leq T_c \text{ do } \) 将\( K_j, V_j\)从HDM加载到SRAM。
第一次内层循环 \(\text{for } 1 \leq j \leq T_r \text{ do } \) 将\( Q_i, O_i, l_i, m_i \)从HDM加载到SRAM。
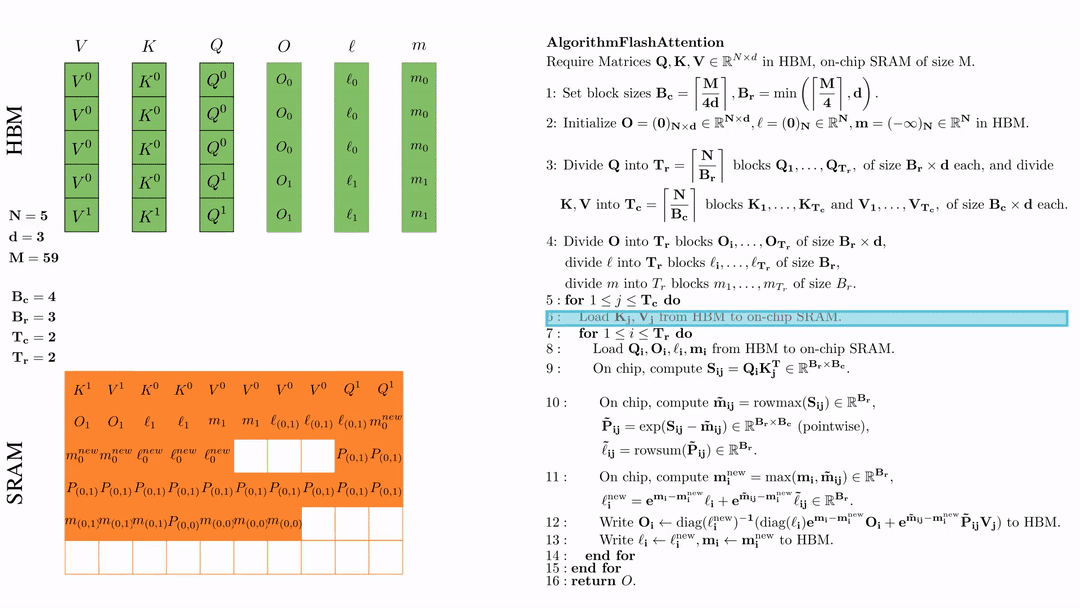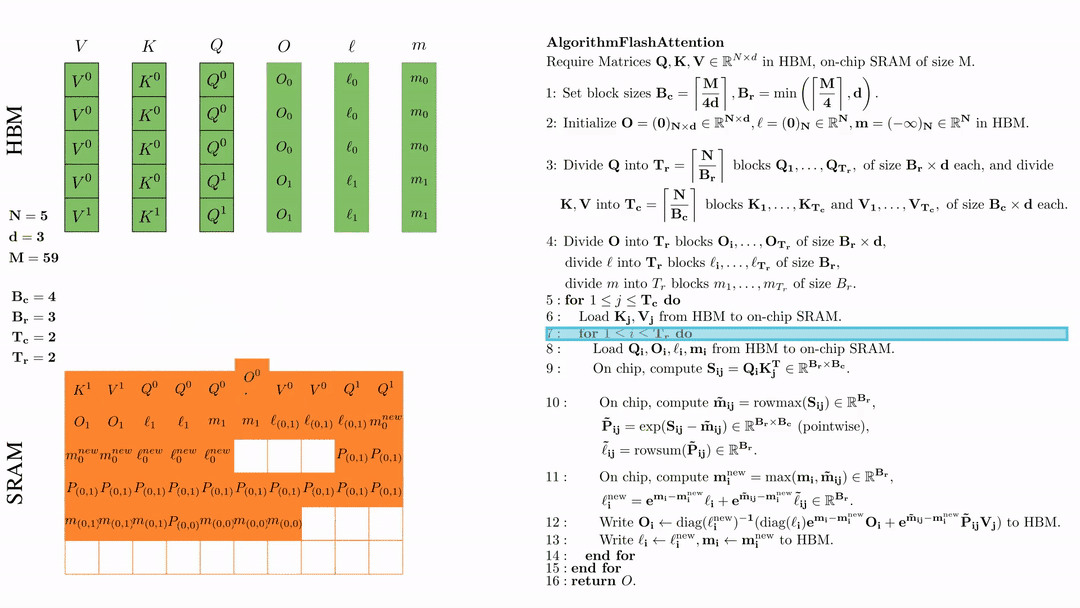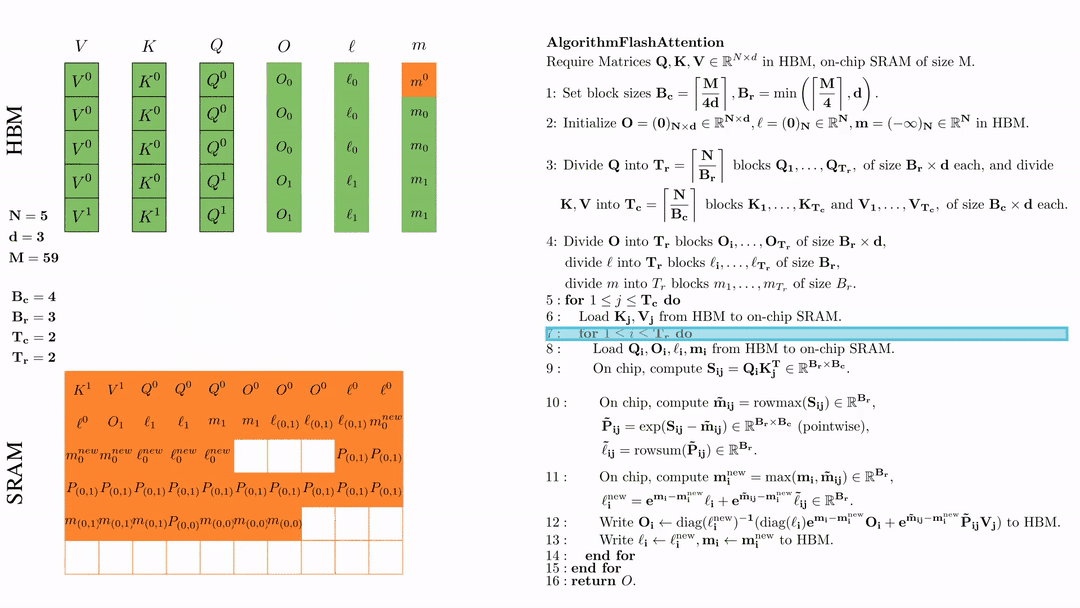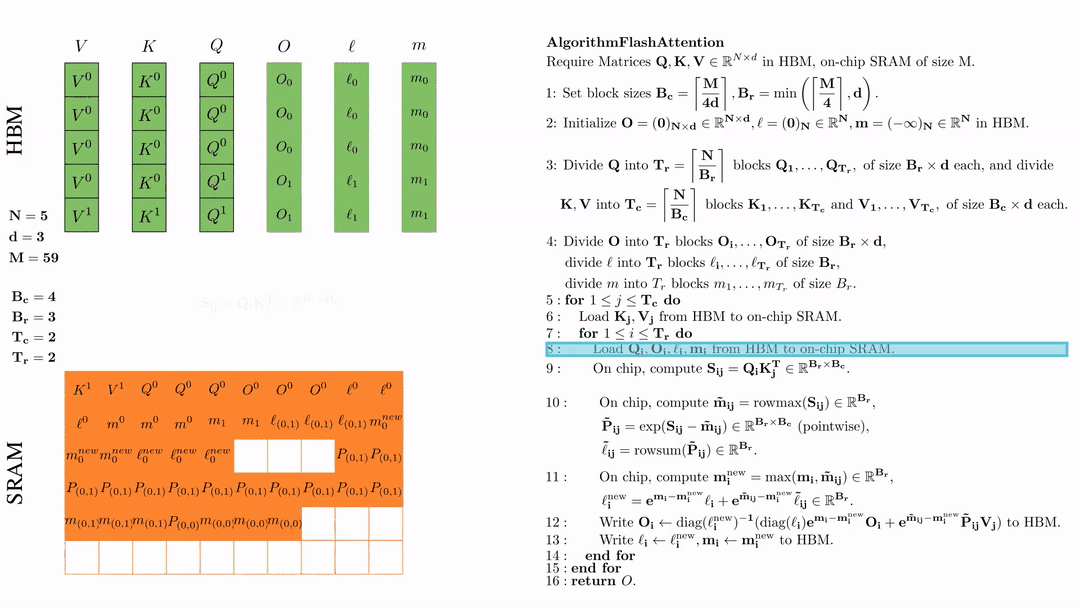
在芯片中,计算\( S_{ij} = Q_i K_j^{\text{T}} \in \mathbb{R}^{B_r \times B_c} \)
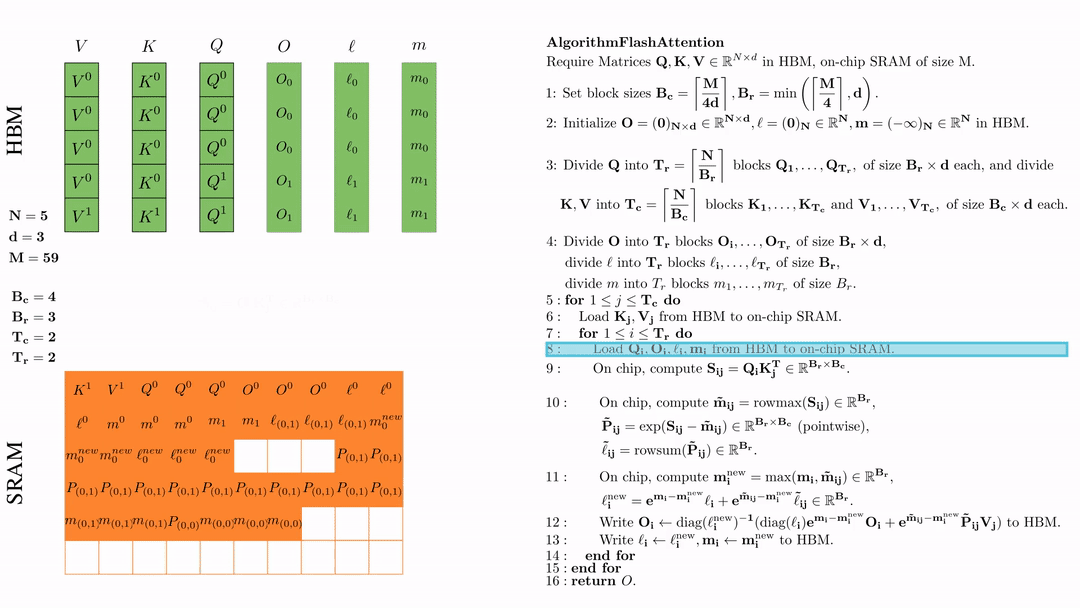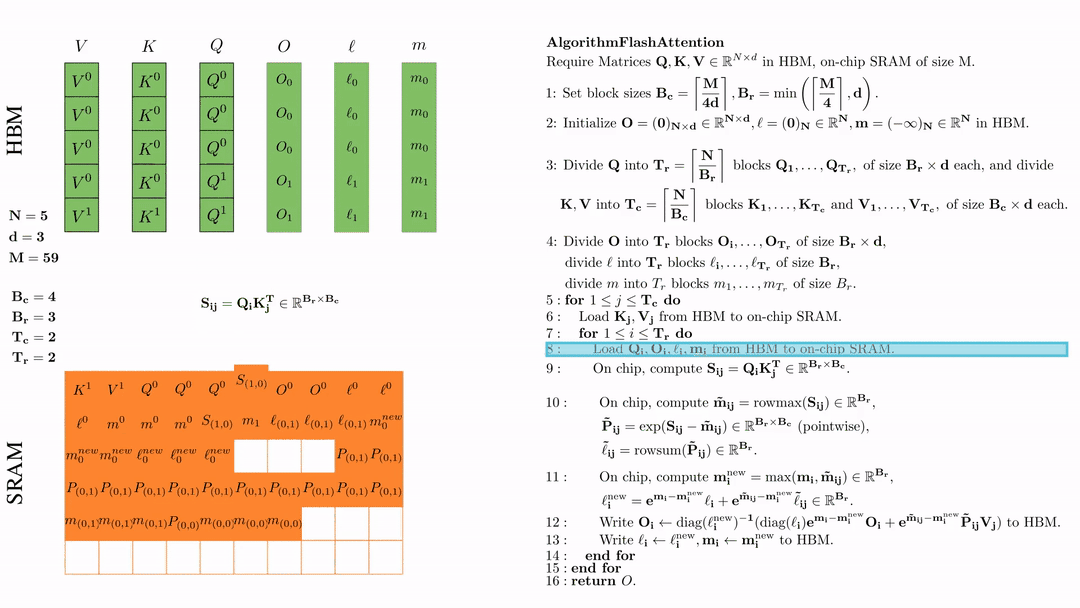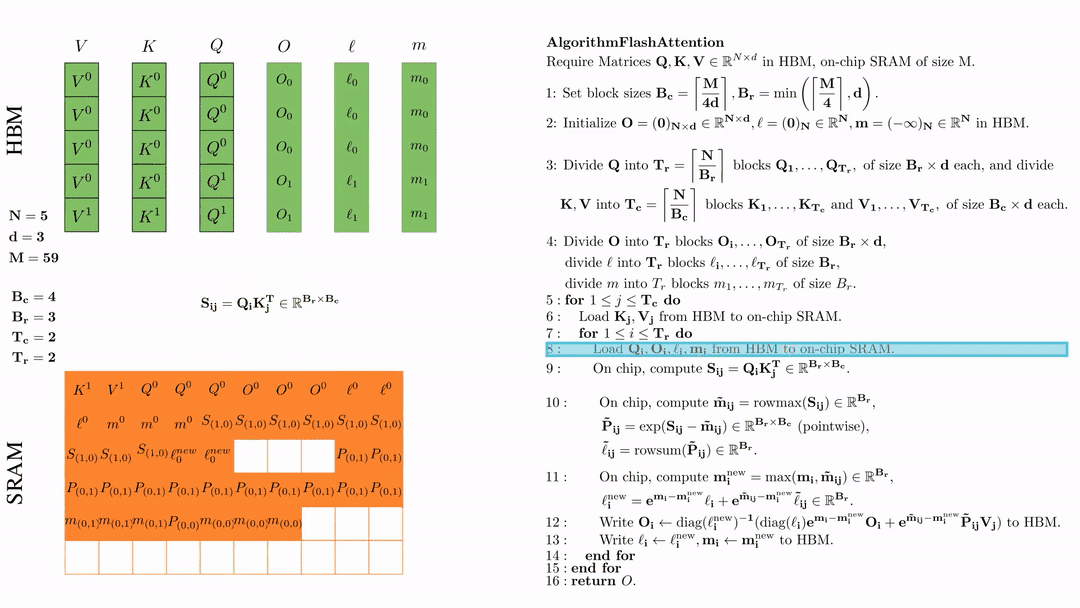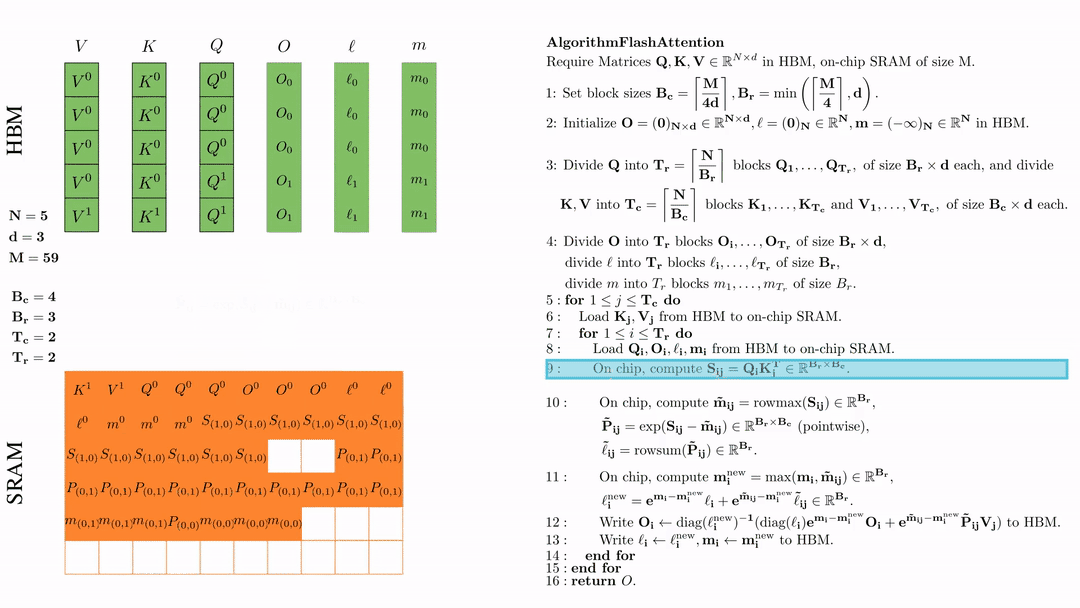
在芯片中,计算 \( \tilde{\mathbf{m}}_{ij} = \text{rowmax}(S_{ij}) \in \mathbb{R}^{B_r} \), \( \tilde{\mathbf{P}}_{ij} = \exp(S_{ij} - \tilde{\mathbf{m}}_{ij}) \in \mathbb{R}^{B_r \times B_c} \ (\text{pointwise}) \), \( \tilde{\ell}_{ij} = \text{rowsum}(\tilde{\mathbf{P}}_{ij}) \in \mathbb{R}^{B_r} \).
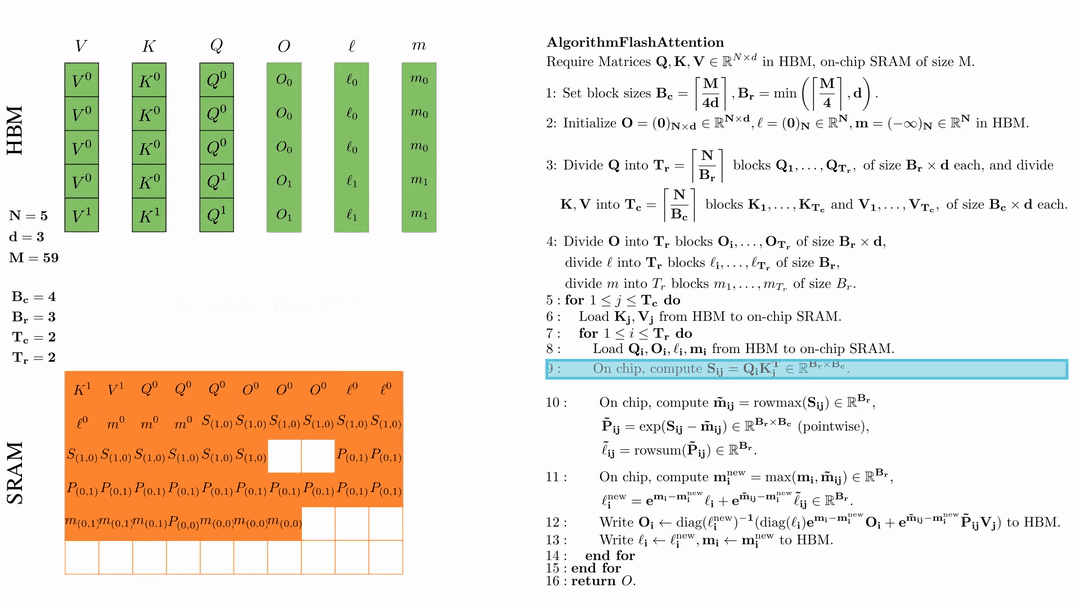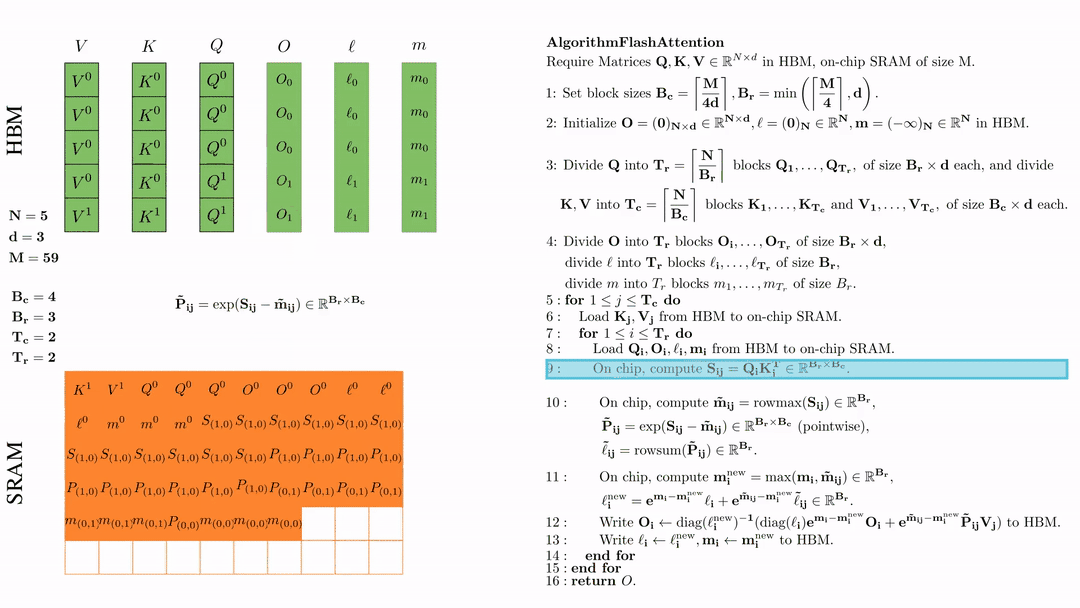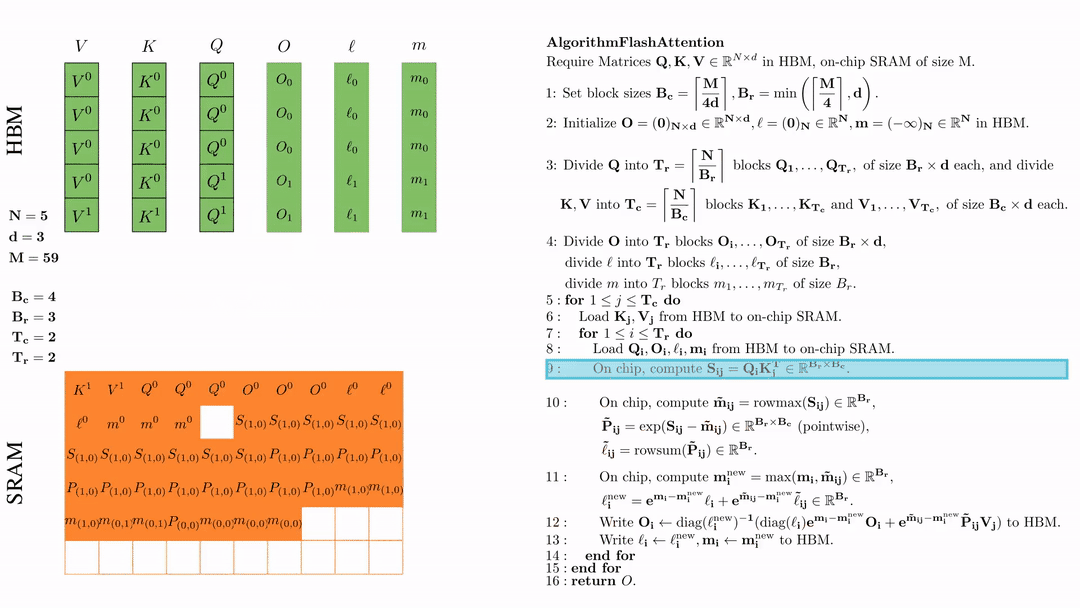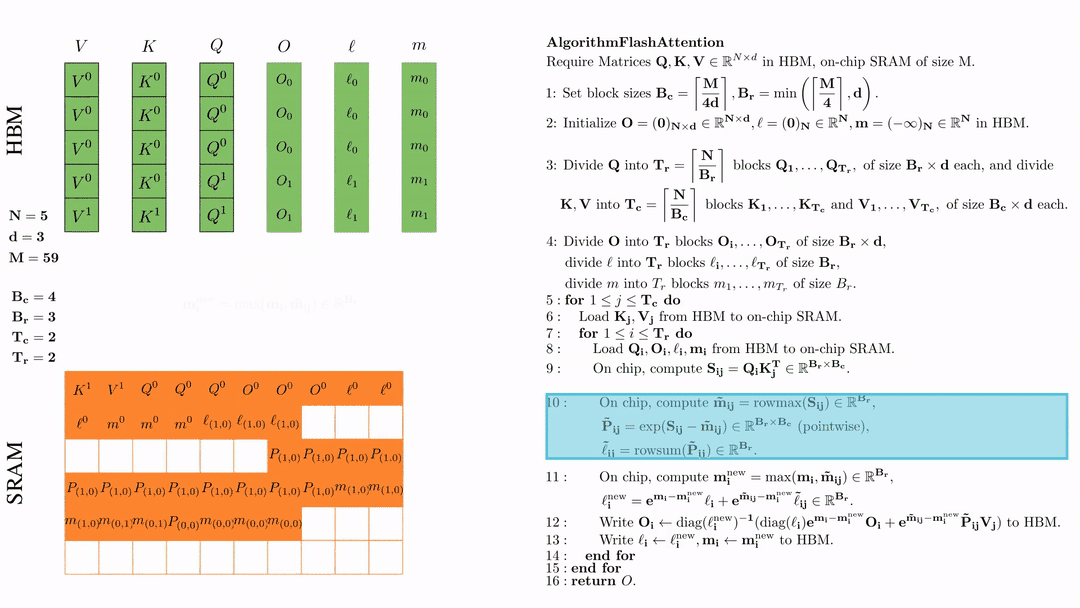
在芯片中,计算 $\mathbf{m}_i^{\text{new}} = \max(\mathbf{m}_i, \tilde{\mathbf{m}}_{ij}) \in \mathbb{R}^{B_r}$, $\ell_i^{\text{new}} = e^{\mathbf{m}_i - \mathbf{m}_i^{\text{new}}} \ell_i + e^{\tilde{\mathbf{m}}_{ij} - \mathbf{m}_i^{\text{new}}} \tilde{\ell}_{ij} \in \mathbb{R}^{B_r}.$
将\( O_i \)更新后写入到HBM,$O_i \leftarrow \text{diag}(l_i^{\text{new}})^{-1} \big( \text{diag}(\ell_i) e^{\mathbf{m}_i - \mathbf{m}_i^{\text{new}}} O_i + e^{\tilde{\mathbf{m}}_{ij} - \mathbf{m}_i^{\text{new}}} \tilde{\mathbf{P}}_{ij} V_j \big)$。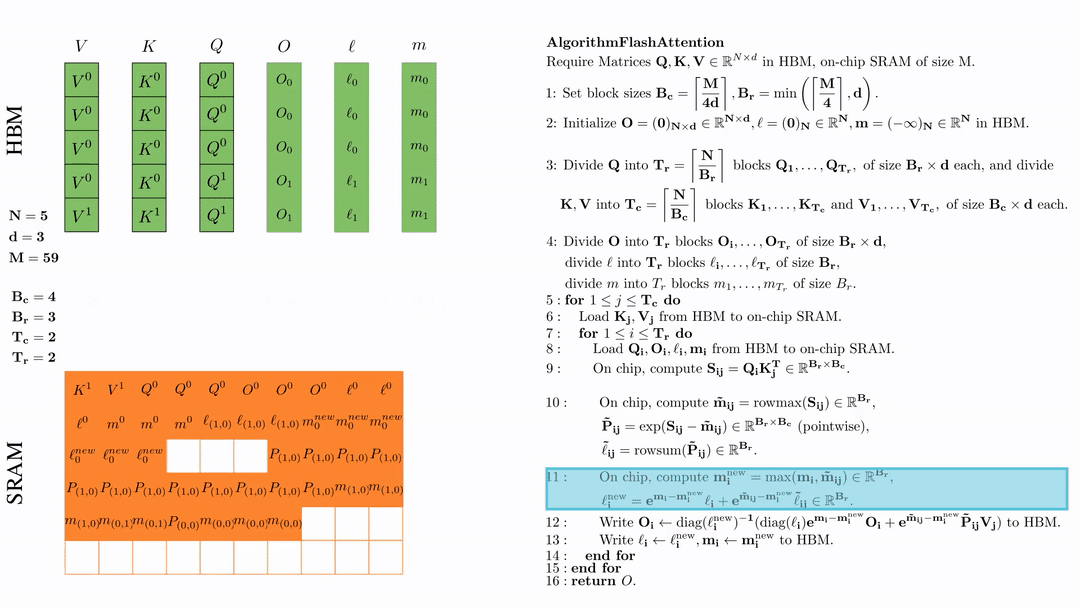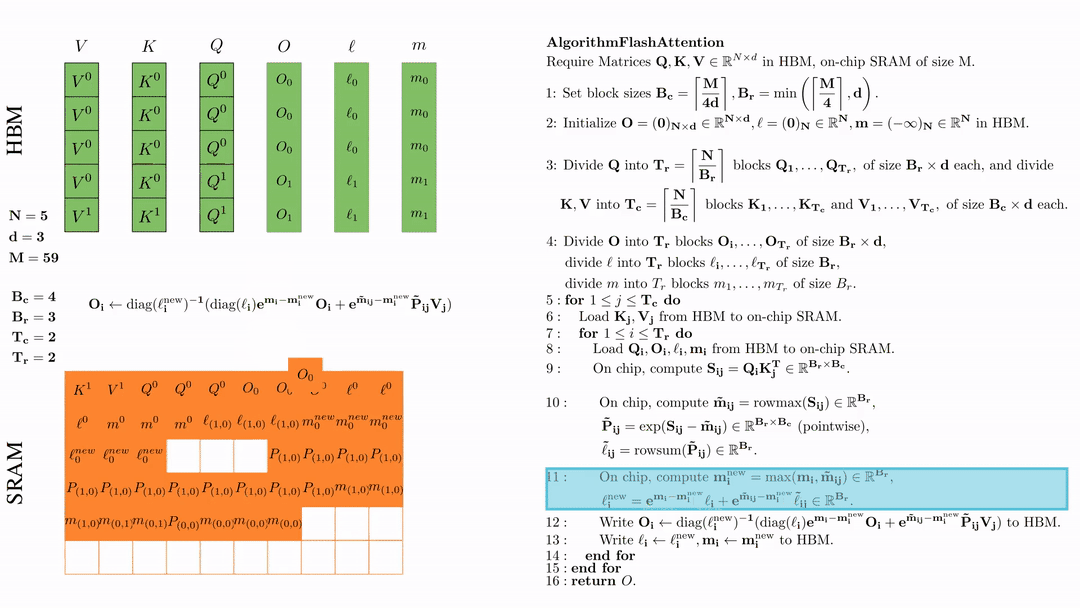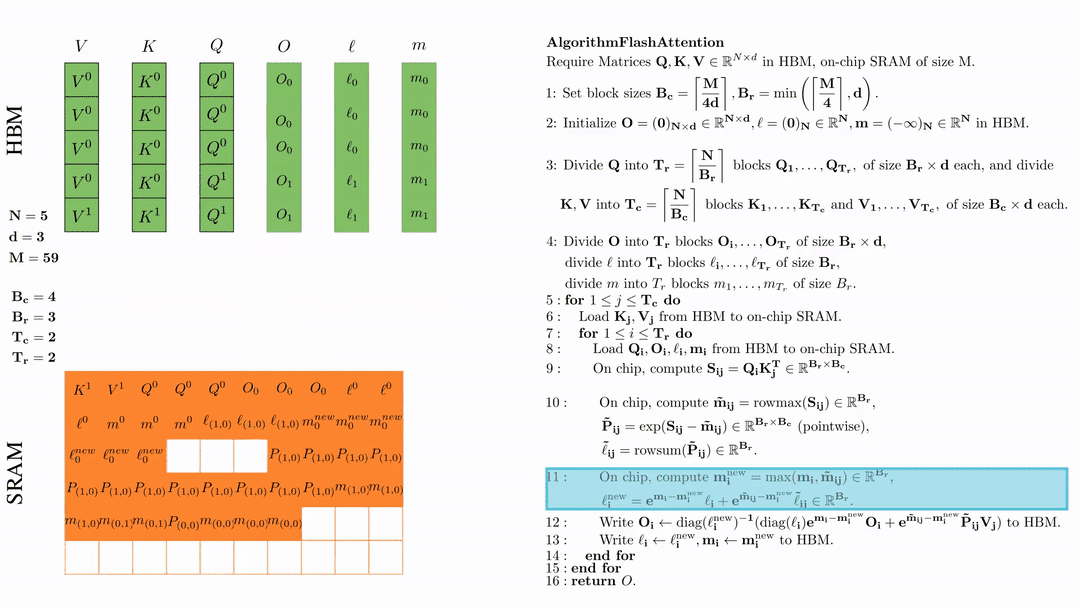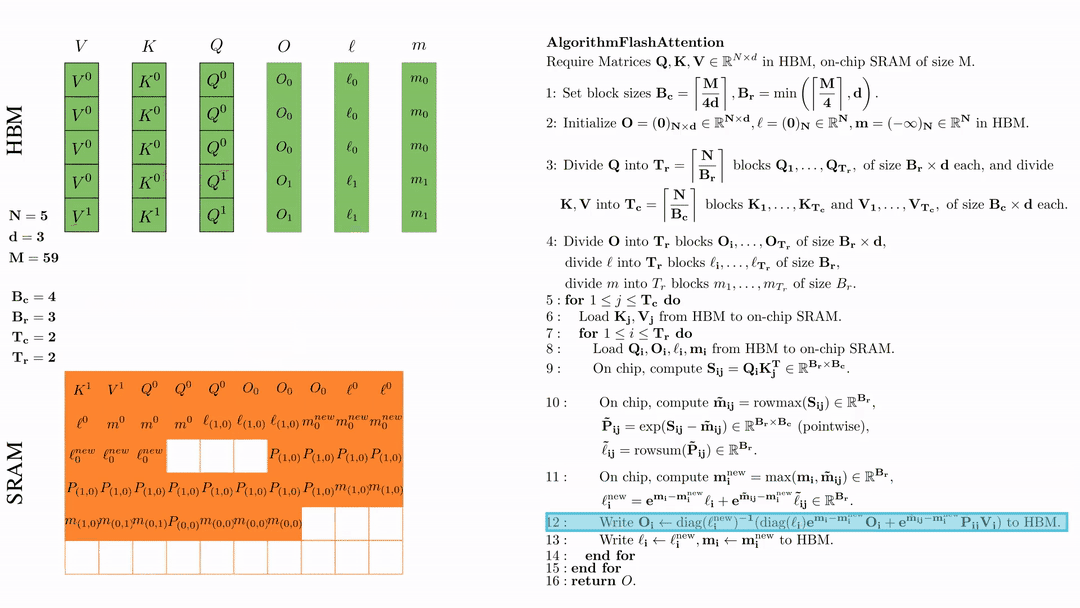
将\( l_i, m_i \)更新后写入HBM,$\ell_i \leftarrow \ell_i^{\text{new}}, \mathbf{m}_i \leftarrow \mathbf{m}_i^{\text{new}}$。

第二次内层循环 \(\text{for } 1 \leq j \leq T_r \text{ do } \) 将\( Q_i, O_i, l_i, m_i \)从HDM加载到SRAM。

在芯片中,计算\( S_{ij} = Q_i K_j^{\text{T}} \in \mathbb{R}^{B_r \times B_c} \)

在芯片中,计算 \( \tilde{\mathbf{m}}_{ij} = \text{rowmax}(S_{ij}) \in \mathbb{R}^{B_r} \), \( \tilde{\mathbf{P}}_{ij} = \exp(S_{ij} - \tilde{\mathbf{m}}_{ij}) \in \mathbb{R}^{B_r \times B_c} \ (\text{pointwise}) \), \( \tilde{\ell}_{ij} = \text{rowsum}(\tilde{\mathbf{P}}_{ij}) \in \mathbb{R}^{B_r} \).

在芯片中,计算 $\mathbf{m}_i^{\text{new}} = \max(\mathbf{m}_i, \tilde{\mathbf{m}}_{ij}) \in \mathbb{R}^{B_r}$, $\ell_i^{\text{new}} = e^{\mathbf{m}_i - \mathbf{m}_i^{\text{new}}} \ell_i + e^{\tilde{\mathbf{m}}_{ij} - \mathbf{m}_i^{\text{new}}} \tilde{\ell}_{ij} \in \mathbb{R}^{B_r}.$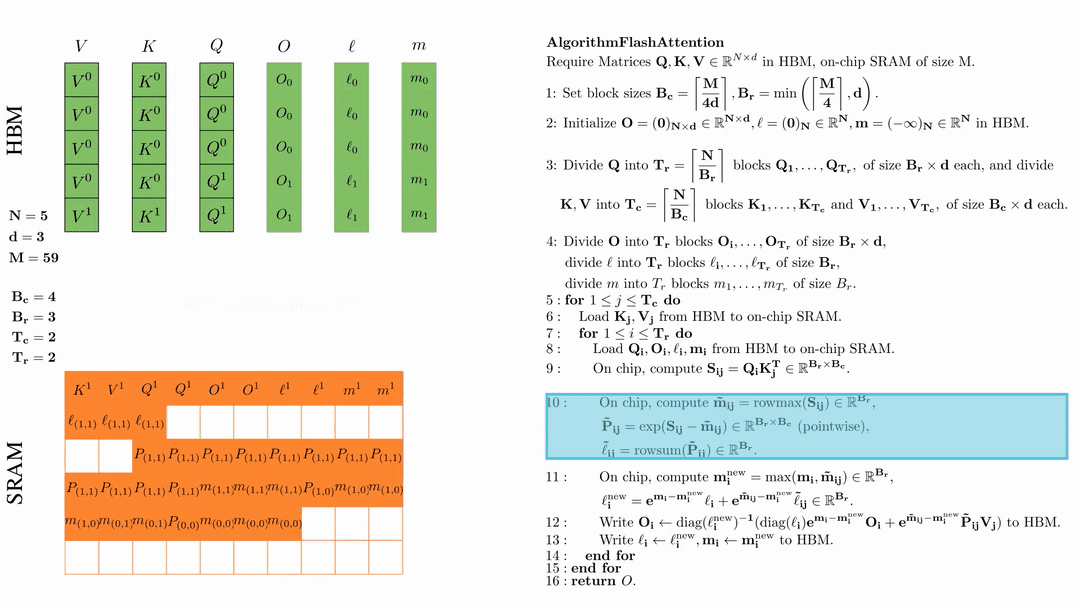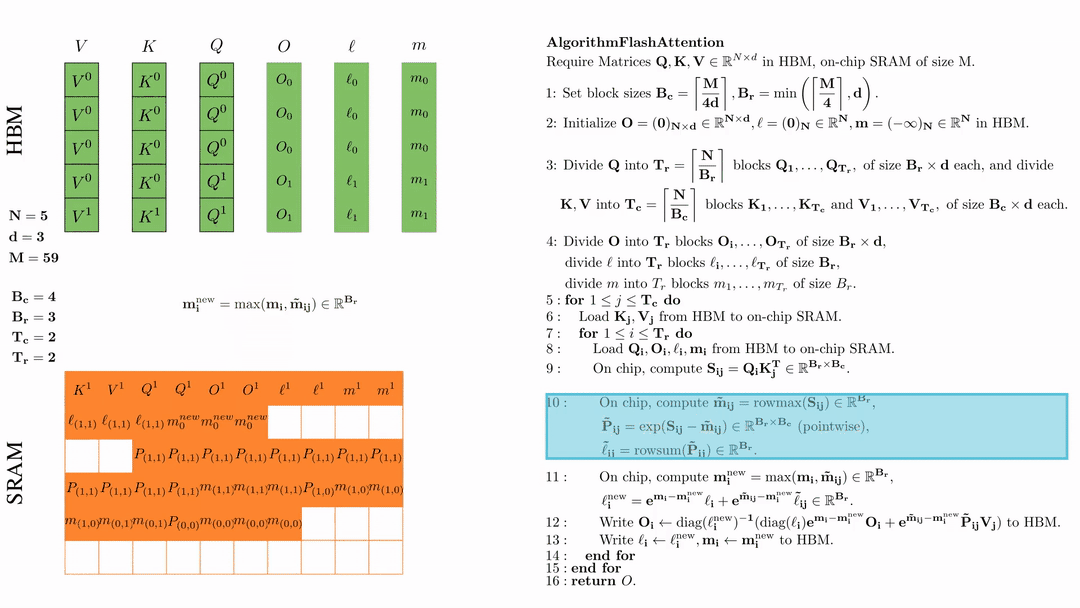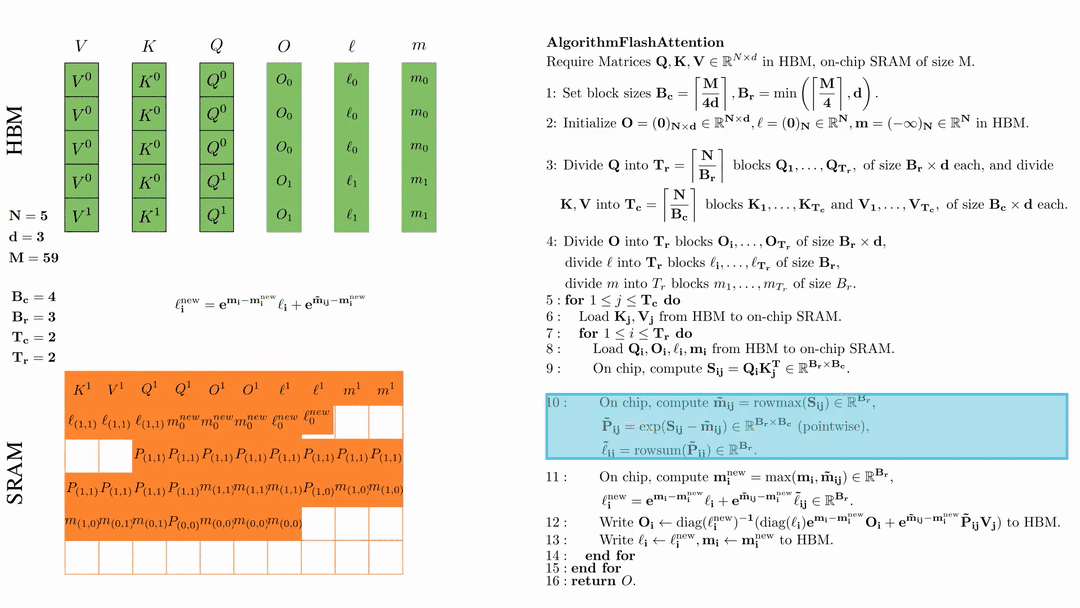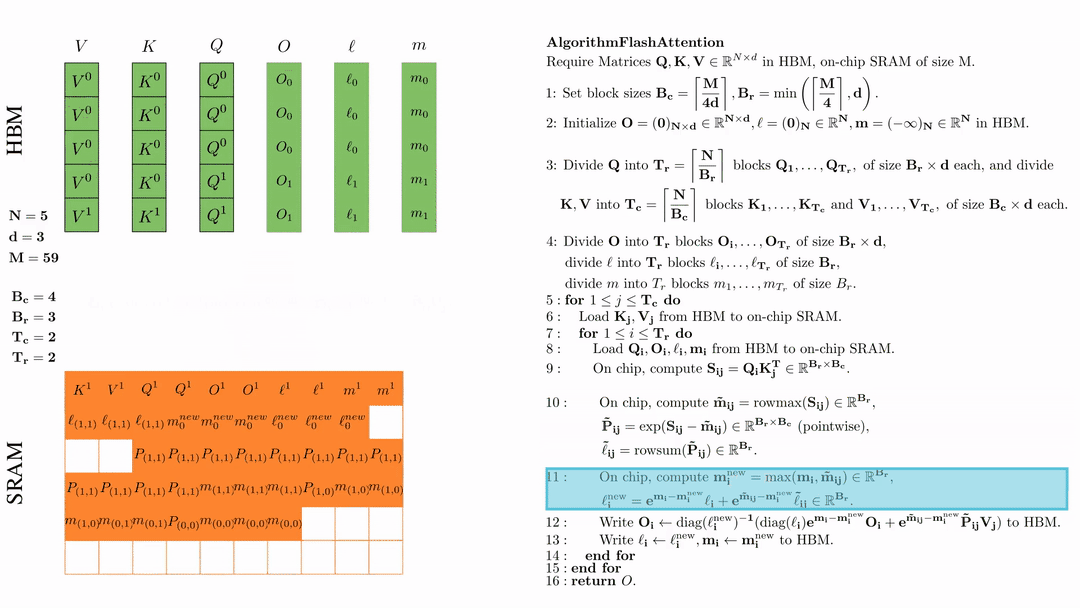
将\( O_i \)更新后写入到HBM,$O_i \leftarrow \text{diag}(l_i^{\text{new}})^{-1} \big( \text{diag}(\ell_i) e^{\mathbf{m}_i - \mathbf{m}_i^{\text{new}}} O_i + e^{\tilde{\mathbf{m}}_{ij} - \mathbf{m}_i^{\text{new}}} \tilde{\mathbf{P}}_{ij} V_j \big)$。
将\( l_i, m_i \)更新后写入HBM,$\ell_i \leftarrow \ell_i^{\text{new}}, \mathbf{m}_i \leftarrow \mathbf{m}_i^{\text{new}}$。
最后返回\( O \).



 浙公网安备 33010602011771号
浙公网安备 33010602011771号